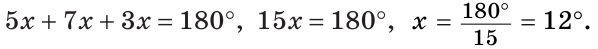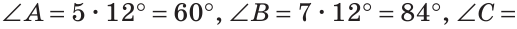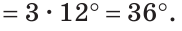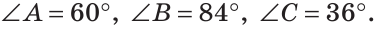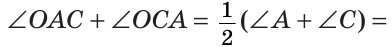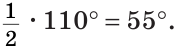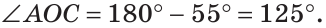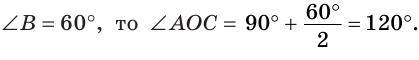Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
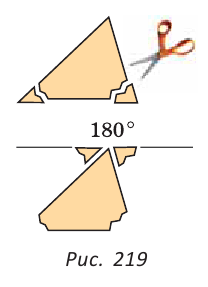
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 
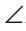
Доказательство:
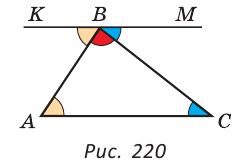
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 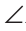
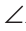
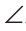
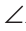
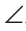





Следствия.
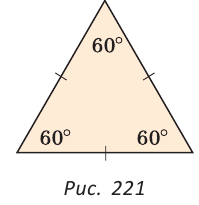
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
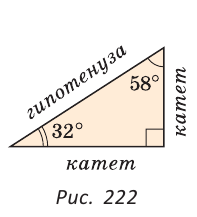
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
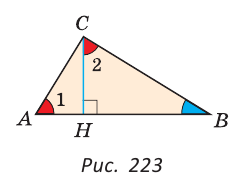
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то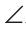
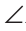
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
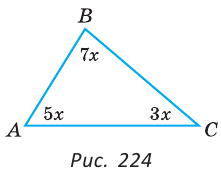
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 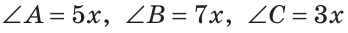
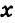
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
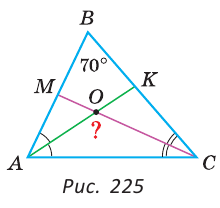
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 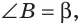
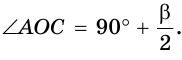
Пример:
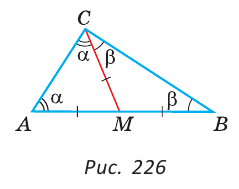
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 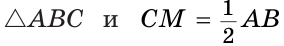
Докажем, что























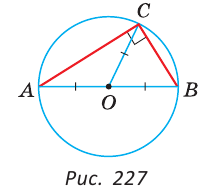
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
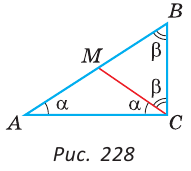
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Чему равна сумма углов выпуклого многоугольникаСкачать

Чему равна сумма углов?
Просто мне нужно объяснить. Но не просто объяснить, а чтобы ещё стало понятно!
Е. Гришковец «Одновременно»
Разговор покупателя с продавцом в магазине «Ткани».
— Здравствуйте! Я шью дома и сама делаю выкройки. Для этого использую угольник с различными углами. Мне нужны чаще всего 90, 60 и 45 градусов, но они у меня в разных угольниках. Приходится перекладывать. Нет ли у вас угольника, в котором были бы именно эти углы?
— Вы знаете, среди тех, что я вижу, нет, но вы заходите, такие должны на днях привезти.
— Большое спасибо, обязательно зайду.
Для математического уха разговор выглядит комично. То, что сумма углов треугольника равна 180°, знают даже школьники, не очень увлечённые математикой. А что такое 180° и почему именно 180? Ясно, скажет умный школьник, это половина от 360, то есть полного оборота.
Невозможно точно сказать, почему окружность была разбита на 360 одинаковых частей и когда это произошло. То ли это персы придумали, у которых год длился 360 дней, то ли вавилоняне, которым удобно было делить окружность на 6 равных частей с помощью равностороннего треугольника.
Была, правда, попытка ввести более логичную, с точки зрения современных представлений о счёте, шкалу для угловых мер. Она делила окружность на 400 равных частей — градов. В этой шкале величина прямого угла равнялась 100 градам. Однако шкала эта не прижилась. Трудно одним желанием изменить пятитысячелетнюю историю цивилизации. Да впрочем, какая разница, в чём мерить, хоть в попугаях, главное — понять, что угол — это некоторая доля от полного оборота.
Почему же сумма углов любого треугольника равна в точности половине полного оборота? Давайте представим себе, что у нас есть три прожектора. Каждый освещает внутренность некоторого угла до бесконечности (жить мы будем временно в двумерном мире). Если мы, стоя в одной точке, включим три прожектора (зелёный, розовый и жёлтый на рисунке), сумма «световых углов» которых равна 180°, и направим их без наложений освещаемой площади, то осветим ровно половину нашего двумерного пространства.
Теперь рассмотрим произвольный треугольник и в вершинах его поставим трёх помощников (Али, Бен и Сирил по буквам вершин, но можно попросить Анну, Варвару и Светлану), доверив им по прожектору. Каждый помощник должен осветить внутренность треугольника лучами света, которые выходят из вершины и продолжаются до бесконечности. Таким образом, каждый прожектор будет освещать внутренность своего угла и не будет освещать внутренность такого же угла, вертикального выбранному. При этом каждая точка плоскости либо попадёт внутрь освещённого угла, либо не будет освещена, попав в вертикальный угол к углу треугольника. Точки же самого треугольника будут освещены трижды. Теперь давайте посмотрим на нашу частично освещённую плоскость с большой высоты (мы-то, как люди трёхмерные, имеем на это право). Если закрыть глаза на небольшой участок перекрытия внутри треугольника, то нетрудно понять, что мы осветили «ровно» половину плоскости. Из чего и можно заключить, что сумма углов произвольного треугольника равна 180°!
Если наше маленькое жульничество внутри треугольника режет глаз, давайте отойдём далеко-далеко от плоскости и забудем, что где-то стоят наши помощники. Нарисуем окружность огромного радиуса с центром где-то внутри треугольника. Какая часть окружности освещена? Ровно (почти) половина. И чем больше радиус нашей окружности, тем меньше будут отличаться освещённая и тёмная части окружности. Ведь каждой светлой дуге будет в пару поставлена такая же тёмная.
Не будем останавливаться на сумме углов треугольника, а попробуем развить эту идею. Самое естественное продолжение — четырёхугольник. Нетрудно понять, что четыре помощника, выполняя аналогичное задание, осветят всю плоскость, что значит: сумма углов четырёхугольника равна 360°. Стоп! Давайте не торопиться, отойдём подальше. Что мы видим? Ужас! Некоторые точки плоскости вообще не освещены. Всё пропало? Не будем паниковать преждевременно. Продолжим наши прямые до бесконечности. На рисунке серым цветом закрашена неосвещённая часть плоскости. Посмотрим внимательно на вертикальный с ней угол. Он освещён, конечно, но освещён дважды! А значит, и здесь всё сходится. Так и должно быть, ведь четырёхугольник можно просто разрезать на два треугольника. Думаем дальше.
Нарисуем пятиконечную звёздочку (не обязательно правильную). Теперь позовём пять фонарщиков, поставим их в вершинах «лучиков» нашей звёздочки, и пусть каждый освещает внутренность того угла, в котором стоит. Соответственно, вертикальный угол освещён не будет. Что мы видим? Картина почти такая же, как у треугольника. Половина плоскости светлая, половина тёмная, а значит, сумма углов пятиконечной звезды равна 180°!
При этом мы нигде не пользовались какими-то особенностями формы этой звёздочки. Более того, а где мы считали количество углов? Давайте внимательно посмотрим на 7-конечную звезду. А потом на 2021-конечную (нарисовать непросто, а представить можно). Что изменится для суммы? Да ничего — половина светлого, половина тёмного. Правда, для большого числа углов нужно «правильно» рисовать звёздочку. Например, для семиугольной конструкции можно привести два примера. Подсчитайте самостоятельно сумму для «более тупоугольной» звёздочки.
Теперь давайте немного развернём наших фонарщиков и дадим им задание осветить один из своих внешних углов. Для начала позовём четверых, поставим их в вершинах выпуклого четырёхугольника. Нетрудно понять, что они осветят всё, кроме самого четырёхугольника. Удаляясь от них, мы поймём, что сумма внешних углов выпуклого четырёхугольника равна 360°.
Также при достаточном удалении мы забудем о количестве помощников, а когда вспомним, поймём, что это совершенно неважно. Сколько бы их ни было, плоскость будет освещена полностью и без перекрытий. Из этого следует чрезвычайно важный и удивительный вывод: сумма внешних углов выпуклого многоугольника равна 360°!
Продолжая применять этот метод, можно получить и другие формулы для суммы углов. То есть если внимательно посмотреть на количество перекрытий, можно вывести формулу для суммы углов выпуклого многоугольника. Но даже без вывода становится понятно, почему сумма внутренних углов зависит от их количества, а сумма внешних нет. Попробуйте развить эту идею на случай невыпуклых многоугольников. Можно, немного поломав голову, найти сумму внутренних углов, а вот для суммы внешних надо сначала понять: что такое внешний угол невыпуклого многоугольника? Успехов в вашем исследовании!
P. S. А угольник 45°, 60° и 90°, оказывается, существует! Это специальный портновский угольник — треугольник, в котором сделаны треугольные дырки с другими углами. И речь в магазине «Ткани», оказывается, совсем не шла о сумме углов треугольника.
Видео:Почему сумма углов треугольника 180 градусов?Скачать

Остроугольный, прямоугольный и тупоугольный треугольники.
Виды треугольников
Остроугольный треугольник — это треугольник,
в котором все углы острые.
Прямоугольный треугольник — это треугольник,
в котором один из углов прямой.
Тупоугольный треугольник — это треугольник,
в котором один из углов тупой.
Как определить вид треугольника
Для того, чтобы понять какой треугольник — остроугольный, прямоугольный или тупоугольный
нужно знать какая градусная мера у углов в треугольнике.
Если один из углов в треугольнике прямой, значит треугольник прямоугольный. Все углы острые в треугольнике — значит треугольник остроугольный. Если в треугольнике один из углов тупой, значит треугольник тупоугольный.
В произвольном треугольнике все углы острые, или два угла острые, а третий прямой или тупой. Если в треугольнике вам известно, что один углов тупой или прямой, значит сумма двух других углов не больше 90 градусов.
В прямоугольном треугольнике стороны напротив острых углов называются катетами, а сторона напротив прямого угла называется гипотенузой.
Градусные меры острого, тупого, прямого углов в треугольниках
Чтобы понять как называется угол и как называется треугольник с этими углами — надо знать его градусную меру:
- Острый угол в любом из треугольников не больше 90 градусов.
- Прямой угол в любом из треугольников равен 90 градусам.
- Тупой угол в любом из треугольников больше 90 градусов, но меньше 180 градусов.
🔥 Видео
Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Сумма углов треугольника равна 180Скачать

Сумма углов треугольникаСкачать

Почему сумма углов в треугольнике 180 градусов? #умскул #егэпрофиль #математикаегэ #математикаСкачать

Сумма углов треугольникаСкачать

Сумма углов 180 градусовСкачать

Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Сумма углов любого треугольника равна 360°. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Сумма углов треугольникаСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать

8 класс, 2 урок, Выпуклый многоугольникСкачать

Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Почему сумма углов в треугольнике равна 180°?Скачать
9 неприятных признаков того, что вы быстро становитесь лучшей версией себяСкачать

Почему сумма углов треугольника 180 градусов? 📚 #егэ #профильнаяматематика #профиль #егэпрофильСкачать
Почему сумма углов треугольника 180? #parta #Базоваяматематика #shortsСкачать

Задача об углах в треугольнике повышенной сложностиСкачать
7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать