Презентация была опубликована 8 лет назад пользователемОльга Анохина
- Похожие презентации
- Презентация на тему: » Тема: Прямоугольные треугольники. Из истории математики. Из истории математики. Прямоугольный треугольник занимает почётное место в вавилонской геометрии,» — Транскрипт:
- Прямоугольный треугольник
- Описание презентации по отдельным слайдам:
- История о прямоугольном треугольнике
- Задачи урока
- План урока
- Прямоугольный треугольник
- Треугольник
- Основные обозначения и формулы треугольника
- Свойства и особенности прямоугольных треугольников
- Признаки прямоугольного треугольника
- Интересные факты о теореме Пифагора
- Из истории математики
- Домашнее задание
- 🎦 Видео
Похожие презентации
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Презентация на тему: » Тема: Прямоугольные треугольники. Из истории математики. Из истории математики. Прямоугольный треугольник занимает почётное место в вавилонской геометрии,» — Транскрипт:
1 Тема: Прямоугольные треугольники
2 Из истории математики. Из истории математики. Прямоугольный треугольник занимает почётное место в вавилонской геометрии, упоминание о нём часто встречается в папирусе Ахмеса. Евклид употребляет выражения: «стороны, заключающие прямой угол», — для катетов; «сторона, стягивающая прямой угол», — для гипотенузы.
3 О истории гипотенузы. Термин гипотенуза происходит от греческого hypoteinsa, означающего тянущаяся под чем либо, стягивающая. Слово берёт начало от образа древнеегипетских арф, на которых струны натягивались на концы двух взаимно перпендикулярных подставок.
4 О истории катета. Термин катет происходит от греческого слова «катетос », которое означало отвес, перпендикуляр. В средние века словом катет означали высоту прямоугольного треугольника, в то время, как другие его стороны называли гипотенузой, соответственно основанием. В XVII веке слово катет начинает применяться в современном смысле и широко распространяется, начиная с XVIII века.
6 Свойство 1 Сумма двух острых углов прямоугольного треугольника равна 90º
7 Свойство 2 Катет прямоугольного треугольника, лежащий против угла в 30º,равен половине гипотенузы.
8 Свойство 3 Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30º
Видео:ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Прямоугольный треугольник
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
С о д е р ж а н и е
Из истории математики
Определения
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Задачи по готовым чертежам
Об авторе
Контрольный тест
Это интересно
Из истории математики
Прямоугольный треугольник занимает почётное место в вавилонской
геометрии, упоминание о нём часто встречается в папирусе Ахмеса.
Термин гипотенуза происходит от греческого hypoteinsa,
означающего тянущаяся под чем либо , стягивающая.
Слово берёт начало от образа древнеегипетских арф, на которых струны
натягивались на концы двух взаимно перпендикулярных подставок.
Термин катет происходит от греческого слова «катетос »,
которое означало отвес , перпендикуляр. В средние века словом катет
означали высоту прямоугольного треугольника, в то время, как другие его
стороны называли гипотенузой, соответственно основанием.
В XVII веке слово катет начинает применяться в современном смысле и
широко распространяется, начиная с XVIII века.
Евклид употребляет выражения:
«стороны, заключающие прямой угол», — для катетов;
«сторона, стягивающая прямой угол», — для гипотенузы.
Определения
Если один из углов треугольника прямой,
то треугольник называется прямоугольным.
А
В
С
Сторона прямоугольного треугольника, лежащая
против прямого угла, называется гипотенузой,
гипотенуза
катет
катет
а две другие – катетами.
Треугольник – это геометрическая фигура,
состоящая из трёх точек, не лежащих на одной
прямой,
и трёх отрезков, соединяющих эти точки.
Некоторые свойства
прямоугольных треугольников
1. Сумма двух острых углов прямоугольного треугольника равна 900.
2. Катет прямоугольного треугольника, лежащий против угла в 300,
равен половине гипотенузы.
3. Если катет прямоугольного треугольника равен половине гипотенузы,
то угол, лежащий против этого катета, равен 300.
Признаки равенства
прямоугольных треугольников
Если катеты одного прямоугольного треугольника
соответственно равны катетам другого, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного
треугольника соответственно равны катету и прилежащему к нему углу
другого, то такие треугольники равны.
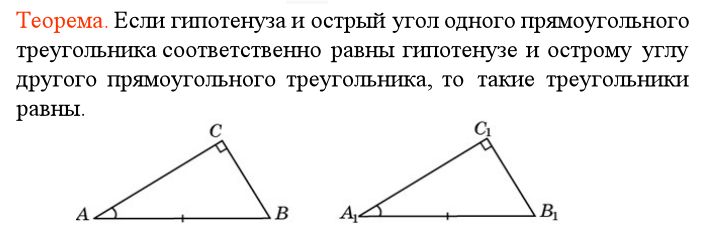
3. Если гипотенуза и острый угол одного прямоугольного треугольника
соответственно равны гипотенузе и острому углу другого,
то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника
соответственно равны гипотенузе и катету другого,
то такие треугольники равны.
Докажем?
Докажем?
Докажем?
Докажем?
Признаки равенства
прямоугольных треугольников
Если катеты одного прямоугольного треугольника
соответственно равны катетам другого, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного
треугольника соответственно равны катету и прилежащему к нему углу
другого, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника
соответственно равны гипотенузе и острому углу другого,
то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника
соответственно равны гипотенузе и катету другого,
то такие треугольники равны.
Докажем?
Докажем?
Докажем?
Докажем?
Если катеты одного прямоугольного треугольника
соответственно равны катетам другого, то такие треугольники равны.
Дано:
Доказать:
Доказательство:
В
А
А1
С
С1
В1
∆ АВС – прямоугольный,
∆ А1В1С1 – прямоугольный,
ВС = В1С1, АС = А1С1 .
∆ АВС = ∆ А1В1С1
следует из первого признака равенства треугольников
(по двум сторонам и углу между ними).
Если катет и прилежащий к нему острый угол одного прямоугольного
треугольника соответственно равны катету и прилежащему к нему углу
другого, то такие треугольники равны.
В
А
А1
С
С1
В1
Дано:
Доказать:
Доказательство:
следует из второго признака равенства треугольников
(по стороне и прилежащим к ней углам)
∆ АВС – прямоугольный,
∆ А1В1С1 – прямоугольный,
АС = А1С1 ,
∆ АВС = ∆ А1В1С1
Если гипотенуза и острый угол одного прямоугольного треугольника
соответственно равны гипотенузе и острому углу другого,
то такие треугольники равны.
В
А
А1
С
С1
В1
Дано:
Доказать:
Доказательство:
т.к. сумма острых углов прямоугольного треугольника равна 90°,
то два других острых угла также равны,
∆ АВС = ∆ А1В1С1
∆ АВС – прямоугольный,
∆ А1В1С1 – прямоугольный,
АВ = А1В1 ,
по второму признаку равенства треугольников
(по стороне и прилежащим к ней углам).
поэтому треугольники равны
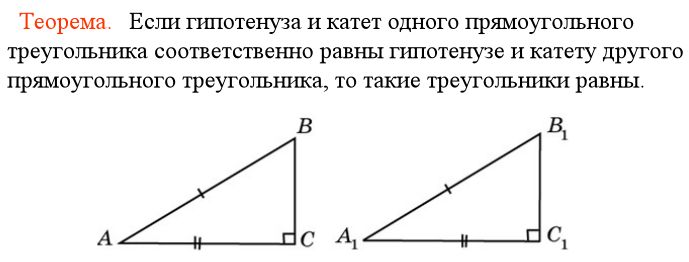
Если гипотенуза и катет одного прямоугольного треугольника
соответственно равны гипотенузе и катету другого,
то такие треугольники равны.
В
А
А1
С
С1
В1
Дано:
Доказать:
Доказательство:
∆ АВС = ∆ А1В1С1
∆ АВС – прямоугольный,
∆ А1В1С1 – прямоугольный,
АВ = А1В1 , АС = А1С1 .
Наложим ∆ А1В1С1 на треугольник ∆ АВС.
Т.к. АС = А1С1 и АВ = А1В1, то они при наложении совпадут.
Тогда вершина А1 совместиться с вершиной А.
Но и тогда и вершины В1 и В также совместятся.
Следовательно, треугольники равны.
Контрольный тест
1. Прямоугольным называется треугольник, у которого
а) все углы прямые;
б) два угла прямые;
в) один прямой угол.
2. В прямоугольном треугольнике всегда
а) два угла острых и один прямой;
б) один острый угол, один прямой и один тупой угол;
в) все углы прямые.
Контрольный тест
3. Стороны прямоугольного треугольника, образующие
прямой угол, называются
а) сторонами треугольника;
б) катетами треугольника;
в) гипотенузами треугольника.
Контрольный тест
4. Сторона прямоугольного треугольника, противолежащая прямому углу, называется
а) стороной треугольника;
б) катетом треугольника;
в) гипотенузой треугольника.
Контрольный тест
Контрольный тест
5. Сумма острых углов прямоугольного треугольника
равна
а) 180°;
б) 100°;
в) 90°.
Об авторе
Данная разработка выполнена учителем математики
МОУ «Средняя общеобразовательная школа № 33» г.Брянска
Кулешовой Галиной Николаевной.
Все отзывы, предложения и вопросы вы можете направить по адресу:
E-maii: galka-kul@yandex.ru
Телефон: 8 – 920 – 607 – 20 – 95
Вернуться к содержанию
Папирус Ахмеса
Математический папирус Ахмеса — древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное около 1650 до н. э. писцом по имени Ахмес на свиток папируса длиной 5,25 м. и шириной 33 см.
Папирус Ахмеса был обнаружен в 1858 шотландским египтологом Генри Риндом и часто называется папирусом Райнда по имени его первого владельца. В 1870 папирус был расшифрован, переведён и издан. Ныне большая часть рукописи находится в Британском музеев Лондоне, а вторая часть — в Нью — Йорке.
Этот документ остается основным источником информации по математике древнего Египта. Он содержит чертежи треугольников с указаниями углов и формулами нахождения площадей.
Во вступительной части папируса Райнда объясняется, что он посвящён «совершенному и основательному исследованию всех вещей, пониманию их сущности, познанию их тайн». Все задачи, приведённые в тексте, имеют в той или другой степени практический характер и могли быть применены в строительстве, размежевании земельных наделов и других сферах жизни и производства. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами, пропорциональное деление, нахождение отношений.
Е В К Л И Д
Евклид (Eνκλειδηζ), древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике.
Сведения об Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в III веке до н. э. Евклид – первый математик александрийской школы. Его главная работа «Начала»
(в латинизированной форме – «Элементы») содержит изложение планиметрии, стереометрии и ряда вопросов теории чисел; в ней он подвел итог предшествующему развитию греческой математики и создал фундамент дальнейшего развития математики.
Из других сочинений по математике надо отметить работу «О делении фигур», сохранившуюся в арабском переводе, четыре книги «Конические сечения», материал которых вошел в произведение того же названия Аполлония Пергского, а также «Поризмы», представление о которых можно получить из «Математического собрания» Паппа Александрийского. Евклид – автор работ по астрономии, оптике, музыке и др.
Дошедшие до нас произведения Евклида собраны в издании «Euclidis opera omnia», ed. J. L. Heibert et Н. Menge, v. 1–9, 1883–1916, дающем их греческие подлинники, латинские переводы и комментарии позднейших авторов.
Это интересно
Треугольник – это многоугольник с тремя сторонами (или тремя углами).
Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.
В любом треугольнике:
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º
4. Продолжая одну из сторон треугольника, получаем внешний угол.
Внешний угол треугольника равен сумме внутренних углов, не смежных с ним.
5. Любая сторона треугольника меньше суммы двух других сторон и
больше их разности ( a b – c; b a – c; c a – b ).
Ответ не правильный.
Более внимательно изучи данную тему!
Вы верно ответили
на все вопросы !
в изучении математики !
Вернуться к содержанию
Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

История о прямоугольном треугольнике
• Проверить у школьников методом опроса знания об усвоенной теме «Треугольник»;
• Расширить знания детей о свойствах и особенностях треугольников;
• Дать знания об основных обозначениях треугольника и его формулах;
• Более детально познакомить учеников с прямоугольным треугольником;
• С помощью решения примеров закрепить знания школьников изученного материала;
• Развивать внимание, логическое мышление и интерес к познаниям математики.
Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Задачи урока
• Закрепить знания учеников о треугольниках и их свойствах;
• Научить применять знания об изученных свойствах при решении задач;
Видео:Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

План урока
1. Прямоугольный треугольник.
2. Треугольники. Повторение темы. Ответы на вопросы.
3. Свойства и особенности прямоугольных треугольников.
4. Признаки прямоугольного треугольника.
5. Основные обозначения и формулы треугольника.
6. Интересные факты.
7. Из истории математики.
6. Задание.
Видео:Высота прямоугольного треугольникаСкачать

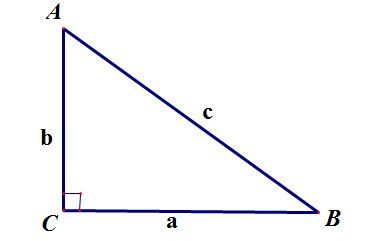
Прямоугольный треугольник
У любого прямоугольного треугольника имеется один угол, который равен 90 градусов. Сторона, которая противоположна прямому углу, имеет название гипотенузы. Гипотенуза является самой большой стороной этого треугольника. Катетами прямоугольного треугольника называются две другие его стороны.
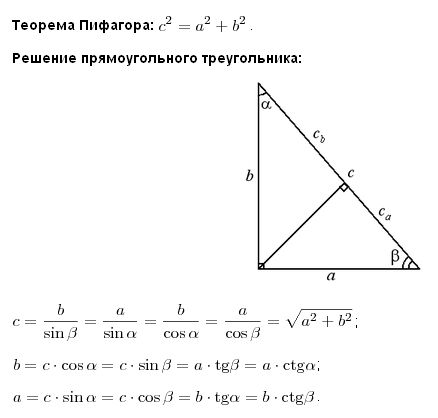
Теорема Пифагора: Для прямоугольных треугольников справедлива теорема Пифагора, согласно которой сумма квадратов катетов равна квадрату гипотенузы.
Видео:Метрические соотношения в прямоугольном треугольнике. 1 часть. 9 класс.Скачать

Треугольник
Треугольник в геометрии представляет одну из основных фигур. Из предыдущих уроков вы знаете, что треугольник – это многоугольная фигура, которая имеет три угла и три стороны.
• Вспомните и ответьте, что является вершинами треугольника?
• Какие разновидности треугольников вы можете назвать?
• Какая отличительная черта разных видов треугольников?
• Что называется катетом прямоугольного треугольника?
• Дайте определение катетам данного треугольника.
• Какой треугольник называется тупоугольным?
• Охарактеризуйте остроугольный многоугольник.
• Что значит косоугольный треугольник?
Видео:ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

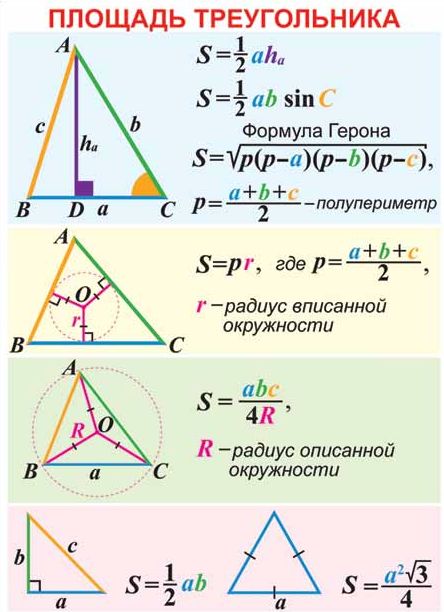
Основные обозначения и формулы треугольника
Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

Свойства и особенности прямоугольных треугольников
I – е свойство. В прямоугольном треугольнике сумма его острых углов равна 90°. Против большей стороны треугольника лежит больший угол, а против большего угла лежит большая сторона.
В прямоугольном треугольнике наибольшим углом, является прямоугольный угол. Если же в треугольнике самый большой угол имеет более 90°, то такой треугольник перестает быть прямоугольным, так как сумма всех углов превысить 180 градусов. Со всего этого следует, что гипотенуза является наибольшей стороной треугольника.
II – е свойство. Катет прямоугольного треугольника, который лежит против угла в 30 градусов, равен половине гипотенузе.
III – е свойство. Если же в прямоугольном треугольнике катет равняется половине гипотенузы, то и угол, который лежит напротив данного катета будет равен 30 градусам.
Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Признаки прямоугольного треугольника
Видео:Медиана в прямоугольном треугольникеСкачать

Интересные факты о теореме Пифагора
• А известно ли вам, что по книге рекордов Гиннеса теорема Пифагора имеет наибольшее число доказательств теоремы и насчитывает их более трех сот.
• А знаете ли вы, что среди всех доказательств теоремы Пифагора существует одно неизвестное доказательство и это доказательство самого автора теоремы, так как оно принадлежит не Пифагору, а Евклиду.
• А представляете ли вы, что оказывается теорема Пифагора, была известна во многих странах еще задолго до древнегреческого философа.
• Один голландский математик пришел к выводу, что заслугой Пифагора не является открытие математики, а ее обоснование и систематизация.
• Происхождение «пифагоровых штанов», вроде как понятно, так как построенные на сторонах треугольника квадраты, которые расходятся в разные стороны, напоминают покрой мужских штанов. Но загадка в другом, оказывается, что в древние греки не знали что такое «штаны», да и сам Пифагор их никогда не носил.
Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Из истории математики
Изображения треугольников и задачи с их применением можно найти на папирусах, найденных в Древней Греции и Египте. Древние мудрецы для облегчения задач стали применять определенные знаки, обозначая ими геометрические фигуры. Так еще в первом веке Герон вместо слов стал использовать треугольник.
Немного позже эта геометрическая фигура одной из первых появилась в изображении орнаментов древних цивилизаций.
Даже в Вавилонской геометрии, такая фигура, как прямоугольный треугольник занимала очень важное и почетное место. Впервые о нем упоминается в папирусе Ахмеса.
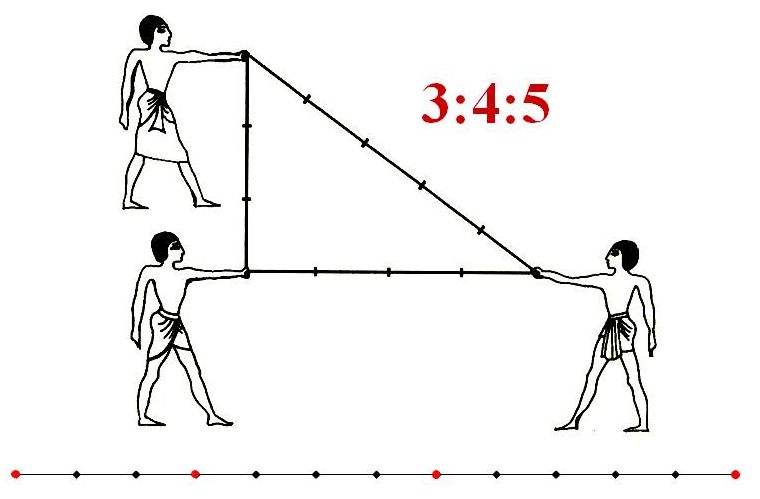
Среди этих прямоугольных треугольников широкое значение имеет египетский треугольник. Что же это за такой египетский треугольник? Оказывается, в египетской архитектуре для построения прямых углов применялось такое соотношение сторон, как 3:4:5. Само название «египетский треугольник» появилось очень давно, вероятно еще в V веке до н.э. Это название произошло именно из Древнего Египта, так местное население широко применяло такой тип треугольника в повседневной жизни и различных сферах деятельности.
Архитекторы и землемеры того времени, чтобы построить прямой угол использовали веревку, которую делили узлами или отметками на двенадцать частей, то есть три плюс четыре и плюс пять. Такой своеобразный треугольник образовывался благодаря натяжению шнура и показывал весьма точную прямоугольную форму, в котором катеты играли роль направляющих для использования в кладке прямого угла нужного сооружения. Благодаря такому изобретению, египетские строители теперь могли более точно делать расчеты для разметки земли под хозяйственные работы и применять их при строительстве пирамид.
Египетский треугольник так же имеет некоторые отличительный особенности. Например, все его стороны и площадь представляю собой целый числа, из-за его прямоугольности он активно применяется в строительстве для отмерения прямых углов. К тому этот уникальный треугольник легко строиться с помощью обыкновенной веревки, как изображено на рисунке.
Но самым важным в феномене египетского треугольника было то, что именно его необычные свойства подтолкнули Пифагора к попытке обобщить каким-то образом все другие прямоугольные треугольники, что и стало в итоге известно под названием теоремы Пифагора!
Задание: Где еще в повседневной жизни можно встретить треугольник?
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Домашнее задание
Продолжите предложение вместо точек:
1. Треугольник называется прямоугольным, если ….
2. У прямоугольного треугольника гипотенузой называется та сторона ….
3. У прямоугольного треугольника большим является ….
Дайте ответы на поставленные вопросы:
1. Какие стороны называются катетами?
2. Какие основные обозначения треугольника?
3. Назовите признаки равенства треугольника?
4. Кто на самом деле открыл теорему Пифагора?
Может ли прямоугольный треугольник иметь:
1. стороны, равные 8, 10, 10?
2. катеты, которые равны 11 см и 111 см?
3. тупой угол?
1. Чему будет равна гипотенуза прямоугольного треугольника, если его стороны равны: 6 см, 8 см, 10 см.
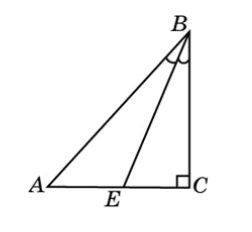
2. Мы имеем прямоугольный треугольник АВС, где угол С прямой. В треугольнике проведена биссектриса ВЕ. Найдите и докажите какой из отрезков больше АЕ или СЕ?
🎦 Видео
Геометрия 7 класс : Свойства прямоугольного треугольникаСкачать

МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ . §15 геометрия 8 классСкачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Прямоугольный треугольник. Часть 2. Высота | Борис Трушин #shortsСкачать

Нахождение стороны прямоугольного треугольникаСкачать

Свойство высоты в прямоугольном треугольникеСкачать

Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать