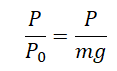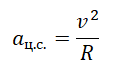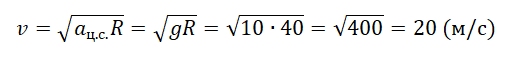Вес тела движущегося по окружности физика

теория по физике 🧲 динамика

Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.

Вес тела имеет электромагнитную природу (не путать с силой тяжести — она возникает между двумя телами и имеет гравитационную природу!). Обозначается P . Измеряется динамометром. Единица измерения — Н (Ньютон).

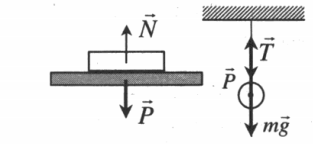
Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P ↑↓ N или P ↑↓ T .

Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:

Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:

Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.

Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.

Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:

P = mg = 16,38∙10 = 163,8 (Н)

Перегрузка

Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.

Перегрузка определяется отношением:

Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.

Вес тела в движущейся равноускоренно системе

Вес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:

1. Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a ↑↑ g —P a ↑↓ g —P > P₀.
2. Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 —P = P₀.

Применение законов Ньютона для определения веса тела

Опора или подвес неподвижны

Второй закон Ньютона в векторной форме:

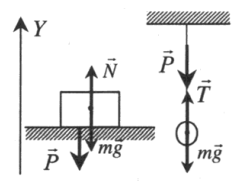
N + m g = m a или T + m g = m a

Проекция на ось ОУ:

N – mg = 0 или T — mg = 0

Ускорение опоры направлено вверх

Второй закон Ньютона в векторной форме:

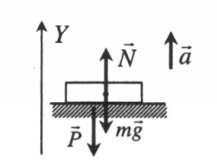
Проекция на ось ОУ:

P = N = ma + mg = m(a + g)

Ускорение опоры направлено вниз

Второй закон Ньютона в векторной форме:

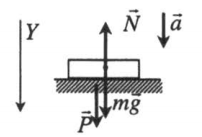
Проекция на ось ОУ:

P = N = mg – ma = m(g – a)

Вершина выпуклого моста

Второй закон Ньютона в векторной форме:

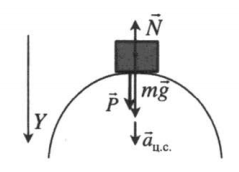
Проекция на ось ОУ:

Нижняя точка вогнутого моста

Второй закон Ньютона в векторной форме:

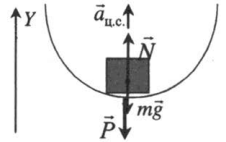
Проекция на ось ОУ:

Полный оборот на подвесе

Второй закон Ньютона в векторной форме:

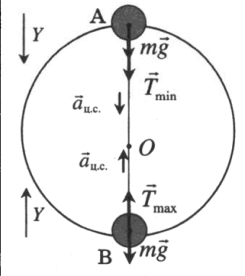
Проекция на ось ОУ в точке А:

Вес тела в точке А:

Проекция на ось ОУ в точке В:

Вес тела в точке В:

Важно! Центростремительное ускорение всегда направлено к центру окружности.

Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?

Вес тела в верхней точке выпуклого моста равен:

Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:

Масса не может быть нулевой, поэтому:

Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:

Отсюда скорость автомобиля в верхней точке моста должна быть равна:

Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…

Вес тела движущегося по окружности

Урок по теме «Динамика движения тел по окружности», 10-й класс

Разделы: Физика

Класс: 10

“Науку все глубже постигнуть стремись,
Познанием вечного жаждой томись.
Лишь первых познаний блеснет тебе свет,
Узнаешь: предела для знания нет.”

Фирдоуси (персидский и таджикский поэт, 940-1030 гг.)

Цель урока: изучение метода решения задач на определение веса тела, движущегося по окружности в вертикальной плоскости.

Задачи урока:

• систематизировать знания по теме: “Вес тела”;
• повторить метод решения задач на определение веса тела, движущегося с ускорением по вертикали;
• научить решать задачи на определение веса тела, движущегося по окружности;
• составить алгоритм решения задач на определение веса тела, движущегося по окружности.

Ход урока

I. Актуализация знаний

Тест на повторение домашнего задания. Ученик выполняет задания теста, обменивается с соседом по парте. В ходе взаимопроверки учащиеся проверяют друг друга и выставляют отметку.

Бланк для заполнения

№ вопроса	1	2	3	4	5
Ответ

Тест на тему “Вес тела”

1. Вес тела — это …
   А. Сила, с которой Земля притягивает к себе тело.
   Б. Сила, с которой опора или подвес действуют на тело.
   В. Сила, с которой вследствие притяжения к земле, тело действует на опору или подвес.
2. На нити висит шарик массой 200 г. Выберите правильное утверждение.
   А. Вес шарика равен 0,2 Н.
   Б. Сила тяжести, действующая на шарик, равна 2 Н.
   В. Если нить перерезать, то вес шарика будет равен силе тяжести, действующей на тело.
3. На полу неподвижного лифта, лежит груз массой 3 кг. Выберите правильное утверждение.
   А. Если лифт начнет двигаться с ускорением вниз, то вес груза будет равен силе тяжести.
   Б. Если лифт начнет двигаться с ускорением вниз, то вес груза будет меньше 30 Н.
   В. Если лифт начнет двигаться с ускорением вниз, то вес груза будет больше 30 Н.
4. Космическая ракета при старте с поверхности Земли движется вверх с ускорением. Вес летчика массой 80 кг будет:
   А. Меньше 800 Н.
   Б. Равен 800 Н.
   В. Больше 800 Н.
5. Тело брошено вертикально вверх. В каком из нижеперечисленных случаев тело находится в состоянии невесомости?
   А. Только при движении вверх.
   Б. Только при движении вниз.
   В. Все время полета.

№ вопроса	1	2	3	4	5
Ответ	В	Б	Б	В	В

II. Объяснение нового материала

Движение по окружности весьма разнообразно. Весь спектр задач для данного вида движения можно условно поделить на два типа:

• движение тел по окружности в вертикальной плоскости (например, движение автомобиля по выпуклому (вогнутому) мосту; вращение тела на веревке; самолет выполняет “ мертвую петлю” и др.)
• движение тел по окружности в горизонтальной плоскости (например, движение ИСЗ; движение транспорта на поворотах; конический маятник и др.)

Под действием двух сил, направленных вдоль одной прямой, тело может двигаться не только по прямой, но и по окружности. Рассмотрим движение тела по окружности под действием силы тяжести и силы упругости.

III. Решение задач

Задача №1. Автомобиль массой 5 т движется по выпуклому мосту со скоростью 36 км/ч.
С какой силой автомобиль давит на середину моста, если радиус кривизны моста составляет 50 м? С какой минимальной скоростью должен двигаться автомобиль, чтобы он не действовал на мост в верхней точке?

Полеты самолетов связаны с фамилией легендарного летчика Петра Николаевича Нестерова.

Сообщение учащегося: Выдающийся летчик Петр Нестеров вошел в историю авиации как довольно яркая фигура. Он основоположник фигурного летания (высшего пилотажа), первый летчик, который доказал возможность осуществлять на самолете маневры в воздухе, в том числе как автор петли, которую назвали его именем.

Выпускник Михайловского артиллерийского училища и Петербургской офицерской воздухоплавательной школы. Военный летчик. Погиб в воздушном бою, впервые применив таран.

“Не для забавы иль задора,
А вас мне нужно убедить,
Что в воздухе везде опора.
Одного хочу лишь я,
Свою петлю осуществляя,
Чтобы “мертвая петля”
Была бы в воздухе “живая”. (П.Н.Нестеров)

Задача №2. (Выполните у доски и в тетрадях)
Самолет делает “мертвую петлю” радиусом 100 м и движется на ней со скоростью
288 км/ч. С какой силой летчик массой 80 кг будет давить на сиденье самолета в нижней точке петли? Какую перегрузку испытывает летчик в этой точке?

IV. Составление алгоритма решения задачи на динамику движения тела по окружности.

• Прочитайте условие задачи и кратко запишите условие задачи.
• Выделите взаимодействующие тела.
• Выполните рисунок, изобразив на нём взаимодействующие тела, покажите с помощью векторов силы, действующие на тело, и ускорение.
• Запишите уравнение второго закона Ньютона в векторной форме.
• Выберите вертикальную ось, направленную вверх или вниз.
• Запишите уравнение второго закона Ньютона в проекциях на выбранную координатную ось.
• Запишите формулу для вычисления центростремительного ускорения.
• Решите в общем виде полученную систему уравнений относительно силы реакции опоры.
• Используя третий закон Ньютона, запишите выражение для веса тела.

• Выразите, если нужно, неизвестную величину.
• Проверьте правильность решения задачи в общем виде путём операций с наименованиями величин, входящих в формулы.
• Подставьте числовые данные в СИ в решение общего вида и произведите вычисления.
• Оцените полученный результат решения.

V. Самостоятельное решение задач в парах.

Вариант 1

Вариант 2Базовый уровень

Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит на сиденье при прохождении им среднего положения со скоростью 6 м/с?

2. Ведерко с водой равномерно вращают в вертикальной плоскости на веревке длиной 0,5 м. С какой наименьшей скоростью нужно его вращать, чтобы при прохождении через верхнюю точку вода не вылилась из ведра?Базовый уровень

1. Автомобиль массой 1500 кг движется по вогнутому мосту, радиус кривизны которого 75 м., со скоростью 15 м/с. Определите вес автомобиля в средней точке моста.

2. С какой скоростью должен лететь самолет в верхней точке “мертвой петли”, чтобы летчик был невесомым, если радиус петли 360 м?

VI. Домашнее задание

§15, решите задачи:

№1. Груз, подвешенный на нити длиной 1 м, раскачивается. Каков вес груза в нижней точке его траектории? Масса груза 1 кг, а его скорость в нижней точке 2 м/с.

№2. В нижней точке “мертвой петли” летчик давит на сиденье кресла с силой 7,1кН. Масса летчика 80 кг, радиус петли 250 м. Определите скорость самолета.

№3. Самолет выходит из пикирования, двигаясь в вертикальной плоскости по дуге окружности радиусом 1 км. Какова скорость самолета в нижней точке траектории, если летчик испытывал пятикратную перегрузку?

Спасибо за работу.

Рефлексия урока

На отдельном листке ответьте на вопросы: 1. Как ты понял тему урока? 2. Оцени свою работу на уроке..

Динамика и кинематика движения по окружности: формулы и решение типовой задачи

Умение описывать движение по окружности является важным для проведения расчетов технических характеристик вращающихся валов и шестерен. Этот вид движения также встречается в быту и природе, например вращение планет вокруг Солнца и фигуристов во время выступления на спортивных соревнованиях. В данной статье рассмотрим, как с точки зрения физики можно описать этот вид движения.

Динамика вращения

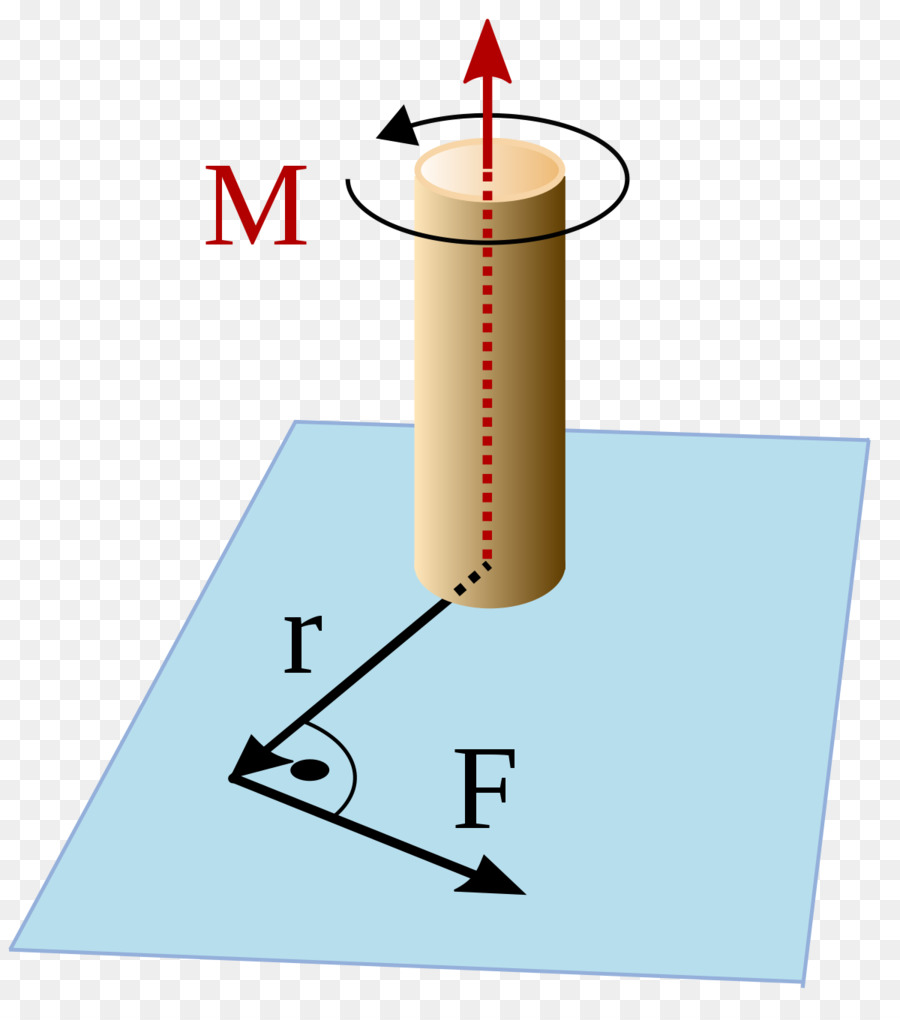
Движение по окружности — это вращение некоторого тела или материальной точки вокруг оси. Чтобы тело начало вращаться, необходимо наличие внешнего момента сил, действующего на рассматриваемую систему. Этот момент определяется по формуле:

Здесь F — сила, d — длина рычага (расстояние между осью и точкой приложения силы). Момент силы является величиной векторной. Приведенная формула используется для расчета модуля M.

Действие момента M отражается на системе в виде появления углового ускорения. То есть система начинает вращаться. Главная формула движения по окружности записывается в виде:

Здесь I — момент инерции, α — ускорение угловое. Обе величины имеют свои аналоги для линейного случая. Если с аналогом величины α все понятно, то для момента инерции I необходимо пояснить. Величина I отражает инерционные свойства вращающейся системы. То есть при вращении она играет такую же роль, как обычная масса тела.

Отметим, что приведенное выражение является аналогом второго закона Ньютона для вращения.

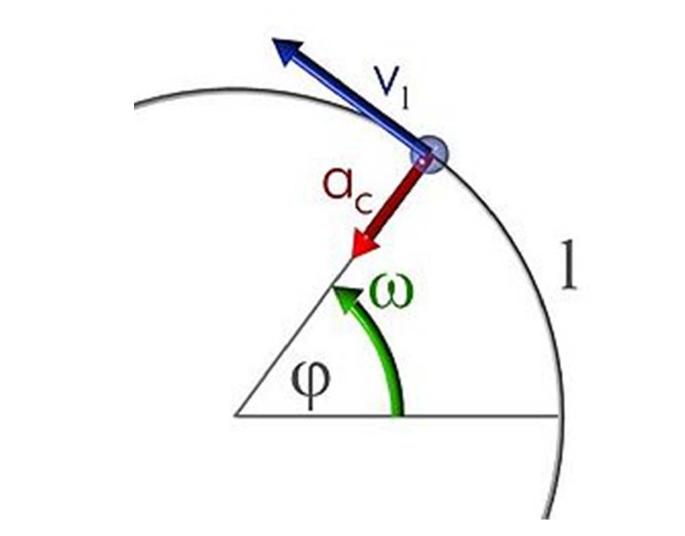
Центростремительная и центробежная силы, ускорение

Процесс вращения предполагает наличие некоторой внутренней силы, которая бы обеспечивала криволинейное движение тела. Эта сила называется центростремительной. Согласно названию, она направлена всегда от тела к оси вращения. Поскольку длина рычага d для нее равна нулю, то к возникновению углового ускорения α она не приводит. Тем не менее она изменяет вектор линейной скорости, то есть создает ускорение.

Ускорение при движении по окружности без изменения модуля линейной скорости называется центростремительным. Оно вычисляется по формуле:

Где v — линейная скорость материальной точки, вращающейся на расстоянии r от оси.

Помимо центростремительной, можно часто услышать и о центробежной силе. Последняя стремится вывести тело из круговой траектории на прямолинейную. Причиной ее появления являются инерционные свойства вращающейся системы.

При движении по окружности центростремительная и центробежная силы по модулю равны друг другу, а по направлению они противоположны.

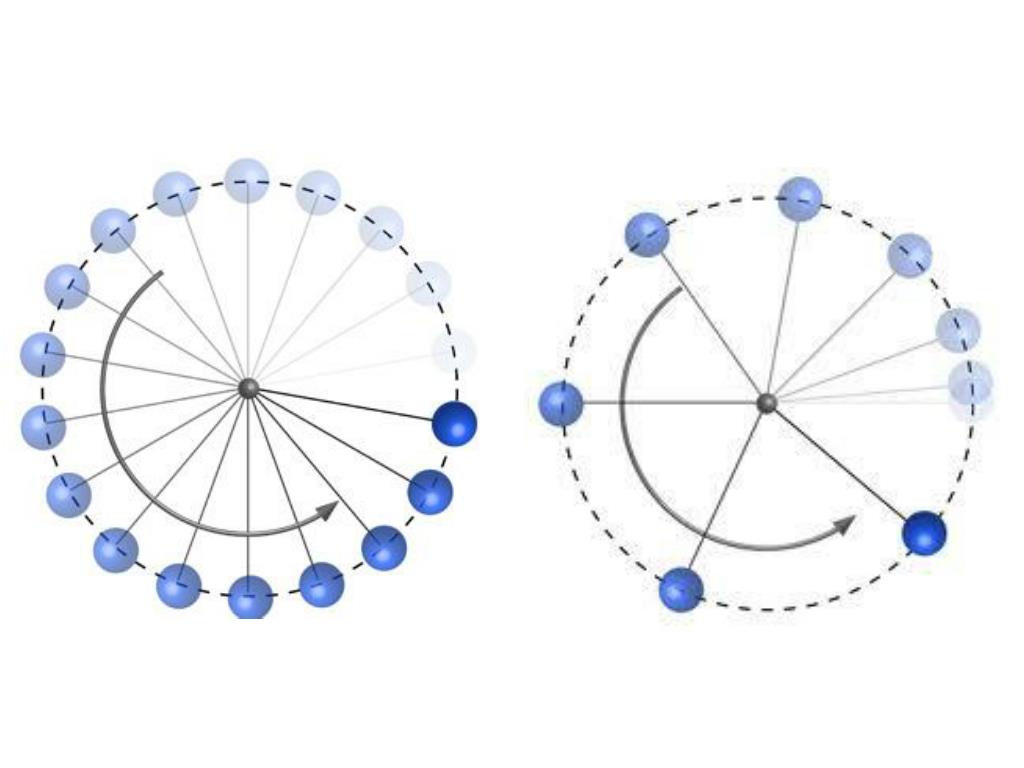
Кинематические уравнения вращения

Движение по окружности, как и по прямой линии, может быть равномерным или происходить с ускорением. В первом случае справедлива формула:

То есть центральный угол θ, на который повернется тело за время t, прямо пропорционален угловой скорости ω. Угол θ выражается в радианах, а скорость ω — в радианах в секунду.

Если действует постоянный внешний момент сил на систему, то движение по окружности происходит с некоторым постоянным ускорением α. В таком случае будет справедливо следующее кинематическое выражение:

Если система сначала вращалась с некоторой скоростью ω_0, а затем стала увеличивать частоту своего вращения с ускорением α, то, начиная с момента времени t, когда появилось ускорение, будет справедлива формула:

Заметим, что это выражение является линейной комбинацией двух предыдущих.

Связь линейных и угловых кинематических характеристик

Выше была приведена формула для центростремительного ускорения, записанная через линейную скорость v. Однако эту формулу можно записать также через соответствующую угловую характеристику ω.

Предположим, что вращающееся тело совершило один оборот по окружности за время t. Тогда для линейной и угловой скоростей можно записать:

Откуда видно, что модуль линейной скорости v в r раз больше модуля величины ω, то есть:

Это равенство связывает угловую и линейную скорости. Используя его, можно записать формулу для a_c через ω:

Теперь вычислим в формуле со скоростями производную по времени для левой и правой частей равенства, получим:

Это равенство связывает направленное по касательной к окружности линейное ускорение a и его угловой аналог α.

Нетрудно доказать, что центральный угол поворота θ при движении по окружности связан с длиной ее дуги L, следующим выражением:

Здесь, если θ будет равен 2*pi радиан (полный оборот), мы получим длину окружности L.

Решение задачи на определение центростремительной силы

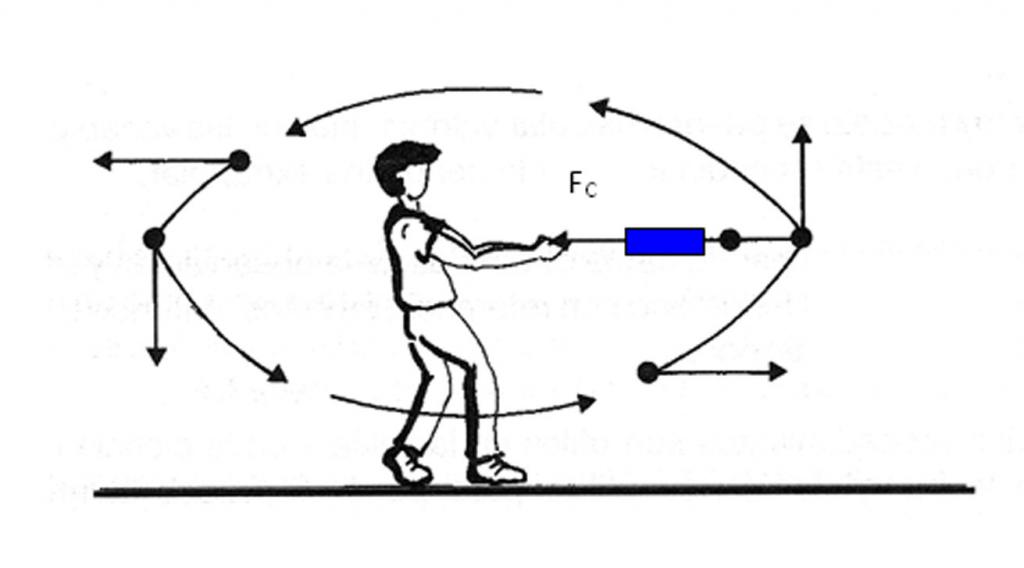
Известно, что к веревке длиной 1 метр привязали камень массой 0,5 кг и стали его вращать с угловой частотой 3 об/с. Необходимо найти силу натяжения веревки F_c.

Сила натяжения F_c является центростремительной. Ее можно вычислить по формуле:

Масса камня m известна. Центростремительное ускорение a_c можно рассчитать из знания угловой скорости ω. С заданной в задаче частотой f величина ω связана выражением:

Тогда центростремительное ускорение будет рассчитываться так:

Искомая сила F_c будет равна:

Если из условия задачи подставить данные в эту формулу, то получится значение силы F_c, приблизительно равное 177,5 Н.

Вес тела движущегося по окружности

Задачи по физике — это просто!

Вспомним

Формулы центростремительного ускорения и центростремительной силы:

Формулы скорости движения тела по окружности и частоты вращения:

Единица измерения частоты вращения — 1/с или оборот/с.

А теперь к задачам!

Элементарные задачи из курса школьной физики на движение по окружности с постоянной по модулю скоростью.

Задача 1

C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?

Задача 2

Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.

Задача 3

Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?

Задача 4

С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?

Задача 5

Чему равно центростремительное ускорение тела, движущегося по окружности радиусом 50 см при частоте вращения 5 оборотов в секунду?

Задача 6

Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.

Задача 7

Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?

Задача 8

Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?

Задача 9

Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.

Вес тела движущегося по окружности физика

Задачи по физике — это просто!

Вспомним

Формулы центростремительного ускорения и центростремительной силы:

Формулы скорости движения тела по окружности и частоты вращения:

Единица измерения частоты вращения — 1/с или оборот/с.

А теперь к задачам!

Элементарные задачи из курса школьной физики на движение по окружности с постоянной по модулю скоростью.

Задача 1

C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?

Задача 2

Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.

Задача 3

Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?

Задача 4

С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?

Задача 5

Чему равно центростремительное ускорение тела, движущегося по окружности радиусом 50 см при частоте вращения 5 оборотов в секунду?

Задача 6

Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.

Задача 7

Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?

Задача 8

Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?

Задача 9

Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.

🔥 Видео