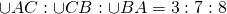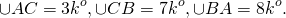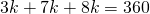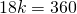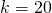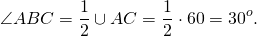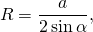Вершины треугольника вписанного в окружность делят его на дуги (3 видео)

Треугольник вписанный в окружность

Содержание

Определение
Формулы
Радиус вписанной окружности в треугольник
Радиус описанной окружности около треугольника
Площадь треугольника
Периметр треугольника
Сторона треугольника
Средняя линия треугольника
Высота треугольника
Свойства
Доказательство
Вершины треугольника делят описанную около него окружность на дуги
Решение №889 Вершины треугольника делят описанную около него окружность на три дуги …
📽️ Видео

Видео:Вершины треугольника делят окружность на три дуги, длины которых относятся как 3:4:11Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Геометрия Вершины треугольника делят описанную около него окружность на три дуги, длины которыхСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

Периметр треугольника вписанного в окружность,
если известны все стороны:

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

Средняя линия треугольника вписанного
в окружность, если известно основание:

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

Высота треугольника вписанного в окружность,
если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Свойства

Центр вписанной в треугольник окружности
находится на пересечении биссектрис.
В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.
Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.
Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров.
Все вершины треугольника, вписанного
в окружность, лежат на окружности.
Сумма всех углов треугольника — 180 градусов.
Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

Проведем серединные
перпендикуляры — HO, FO, EO.
O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.
Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:ОГЭ 2022 Математика Задача 23 Вариант 11 Ященко 36 вариантовСкачать

Вершины треугольника делят описанную около него окружность на дуги

Если вершины треугольника делят описанную около него окружность на три дуги, как найти её радиус?

Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найти радиус окружности, если меньшая из сторон треугольника равна 20.

Дано: ∆ABC,

окр (O: R) — описанная,

Пусть k — коэффициент пропорциональности. Тогда дуги, на которые точки A, B и C делят окружность, равны

Так как градусная мера всей окружности равна 360º, то

Значит, градусная мера наименьшей дуги AC равна 3∙20=60º.

Так как вписанный угол равен половине дуги, на которую он опирается, а угол ABC опирается на дугу AC, то

радиус описанной около треугольника ABC окружности равен

Видео:Вершины треугольника делят окружность на три дуги, длины которых относятся как 6:13:17Скачать

Решение №889 Вершины треугольника делят описанную около него окружность на три дуги …

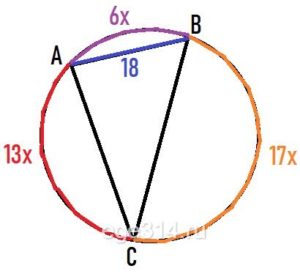
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 6:13:17. Найдите радиус окружности, если меньшая из сторон равна 18.

Длины дуг относятся как 6:13:17. Значит и градусные меры дуг относятся как 6:13:17.
Пусть ‿АВ = 6х, ‿АС = 13х, ‿ВС =17х. Вся окружность равна 360°. Найдём градусную меру ‿АВ: