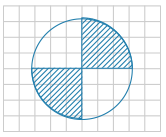
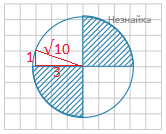
На клетчатой бумаге с размером клетки 1 см × 1 см изображена окружность. Вычислите площадь закрашенной фигуры в см 2 . В ответ укажите [math]frac Spi[/math].
Используя теорему Пифагора по клетчатой бумаге определяем радиус круга √10. Площадь закрашенной фигуры равны половине площади круга
В ответ [math]frac Spi=fracpi=5[/math]
Ответ: 5
2 1 8 0 5 6 8
Видео:На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

На клетчатой бумаге с размером 1х1 изображена окружность
На клетчатой бумаге с размером клетки 1 × 1 изображён вписанный в окружность угол ABC. Найдите его градусную величину.
Аналоги к заданию № 27890: 26237 27891 509571 Все
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Отрежем от закрашенной фигуры сектор, отмеченный синим цветом, и добавим к ней сектор, выделенный красным цветом. Указанные секторы равны, поэтому площадь фигуры не изменилась. Следовательно, она равна трём четвертям площади круга, радиус которого см. Поэтому
см 2 .
Хотелось бы более «научного» доказательства. Аргумент «это видно» не достаточен, так как всем видно разное. Спасибо!
На рисунке ВИДНО, что они равны. Или задайте прямые уравнениями и
и найдите угол между ними. Но то, что уравнения именно такие, тоже ВИДНО по рисунку. Задания на работу с рисунками предполагают считывание информации с рисунка.
На клетчатой бумаге с размером клетки 1 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.
Треугольник прямоугольный, значит, радиус описанной вокруг него окружности равен половине гипотенузы.
Видео:Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки 
Средняя линия трапеции равна полусумме её оснований:
2. Найдите величину угла ABC. Ответ дайте в градусах.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:
Осталось умножить найденное значение синуса на
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 
Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

Получим:
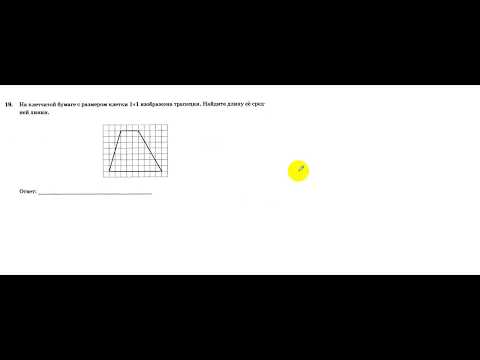
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 
Площадь трапеции равна произведению полусуммы оснований на высоту:
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:
Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 — 4 = 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.
На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.
Значит, нам надо умножить площадь круга на . Получим:
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.
Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
14. Найдите площадь четырехугольника, вершины которого имеют координаты
На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
🌟 Видео
На клетчатой бумаге с ром клетки 1 на 1 изображён равносторонний треугольник. Найдите радиус описаннСкачать

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.Скачать
На клетчатой бумаге с размером клетки 1 × 1 изображена ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольник ABCD. Найдите радиус окружностиСкачать

На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

ОГЭ по математике На клетчатой бумаге с размером 1х1 изображен параллелограммСкачать

Вариант 2 Задание 3 ЕГЭ 2016 Математика, И В Ященко 36 вариантов Решение ОтветСкачать

Самый простой способ нахождения площадиСкачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

№ 104. Клетчатая бумага. Задание 3. ЕГЭ. Математика. Профильная.Скачать

На клетчатой бумаге с размером клетки 1 × 1 изображена ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

На клетчатой бумаге изображен треугольник. Найдите радиус описаннойСкачать

На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

3 задача по геометрии на ЕГЭ / Как решается геометрическая задача на ЕГЭ 2021 по математике?Скачать

ОГЭ, математика, задание 18| Треугольник на клетчатой бумагеСкачать
ОГЭ по математике. Задание 15Скачать

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.Скачать

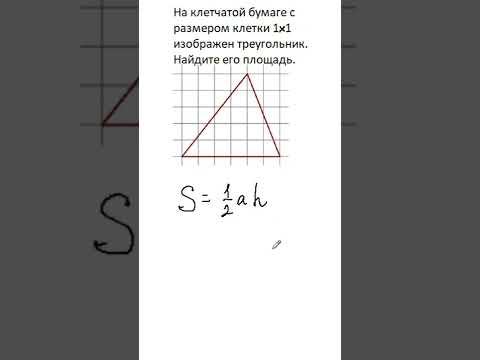
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.Скачать