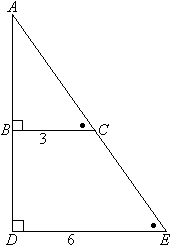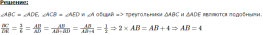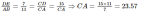Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Определение
Как правило, два треугольника считаются подобными если они имеют одинаковую форму, даже если они различаются размерами, повернуты или даже перевернуты.
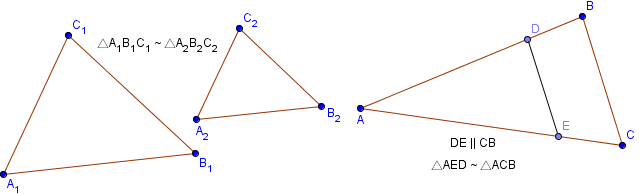
Математическое представление двух подобных треугольников A1B1C1 и A2B2C2 , показанных на рисунке, записывается следующим образом:
Два треугольника являются подобными если:
1. Каждый угол одного треугольника равен соответствующему углу другого треугольника:
∠A1 = ∠A2, ∠B1 = ∠B2 и∠C1 = ∠C2
2. Отношения сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой:
$frac=frac=frac$
3. Отношения двух сторон одного треугольника к соответствующим сторонам другого треугольника равны между собой и при этом
углы между этими сторонами равны:
$frac=frac$ и $angle A_1 = angle A_2$
или
$frac=frac$ и $angle B_1 = angle B_2$
или
$frac=frac$ и $angle C_1 = angle C_2$
Не нужно путать подобные треугольники с равными треугольниками. У равных треугольников равны соответствующие длины сторон. Поэтому для равных треугольников:
Из этого следует что все равные треугольники являются подобными. Однако не все подобные треугольники являются равными.
Несмотря на то, что вышеприведенная запись показывает, что для выяснения, являются ли два треугольника подобными или нет, нам должны быть известны величины трех углов или длины трех сторон каждого треугольника, для решения задач с подобными треугольниками достаточно знать любые три величины из указанных выше для каждого треугольника. Эти величины могут составлять различные комбинации:
1) три угла каждого треугольника (длины сторон треугольников знать не нужно).
Или хотя бы 2 угла одного треугольника должны быть равны 2-м углам другого треугольника.
Так как если 2 угла равны, то третий угол также будет равным.(Величина третьего угла составляет 180 — угол1 — угол2)
2) длины сторон каждого треугольника (углы знать не нужно);
3) длины двух сторон и угол между ними.
Далее мы рассмотрим решение некоторых задач с подобными треугольниками. Сначала мы рассмотрим задачи, которые можно решить непосредственным использованием вышеуказанных правил, а затем обсудим некоторые практические задачи, которые решаются по методу подобных треугольников.
Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Практические задачи с подобными треугольниками
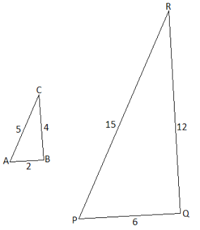
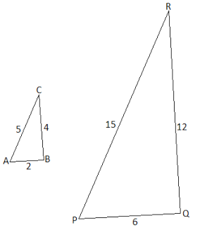
Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.
Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить второе правило:
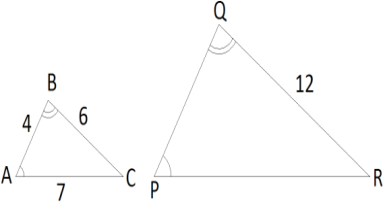
Пример №2: Покажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.
Решение:
∠A = ∠P и ∠B = ∠Q, ∠C = ∠R(так как ∠C = 180 — ∠A — ∠B и ∠R = 180 — ∠P — ∠Q)
Из этого следует, что треугольники ΔABC и ΔPQR подобны. Следовательно:
$frac=frac=frac$
Пример №3: Определите длину AB в данном треугольнике.
Решение:
∠ABC = ∠ADE, ∠ACB = ∠AED и ∠A общий => треугольники ΔABC и ΔADE являются подобными.
$frac = frac = frac = frac = frac = frac Rightarrow 2times AB = AB + 4 Rightarrow AB = 4$
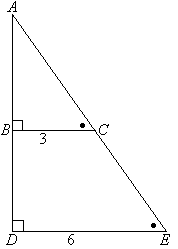
Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.
Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.
AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC
Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.
Следовательно:
$frac = frac = frac = frac Rightarrow CA = frac = 23.57$
x = AC — DC = 23.57 — 15 = 8.57
Практические примеры
Пример №5: На фабрике используется наклонная конвеерная лента для транспортировки продукции с уровня 1 на уровень 2, который выше уровня 1 на 3 метра, как показано на рисунке. Наклонный конвеер обслуживается с одного конца до уровня 1 и с другого конца до рабочего места, расположенного на расстоянии 8 метров от рабочей точки уровня 1.
Фабрика хочет модернизировать конвеер для доступа к новому уровню, который находится на расстоянии 9 метров над уровнем 1, и при этом сохранить угол наклона конвеера.
Определите расстояние, на котором нужно установить новый рабочий пункт для обеспечения работы конвеера на его новом конце на уровне 2. Также вычислите дополнительное расстояние, которое пройдет продукция при перемещении на новый уровень.
Решение:
Для начала давайте обозначим каждую точку пересечения определенной буквой, как показано на рисунке.
Исходя из рассуждений, приведенных выше в предыдущих примерах, мы можем сделать вывод о том, что треугольники ΔABC и ΔADE являются подобными. Следовательно,
$frac = frac = frac = frac Rightarrow AB = frac = 24 м$
x = AB — 8 = 24 — 8 = 16 м
Таким образом, новый пункт должен быть установлен на расстоянии 16 метров от уже существующего пункта.
А так как конструкция состоит из прямоугольных треугольников, мы можем вычислить расстояние перемещения продукции следующим образом:
Аналогично, $AC = sqrt = sqrt = 25.63 м$
что является расстоянием, которое проходит продукция в данный момент при попадании на существующий уровень.
y = AC — AE = 25.63 — 8.54 = 17.09 м
это дополнительное расстояние, которое должна пройти продукция для достижения нового уровня.
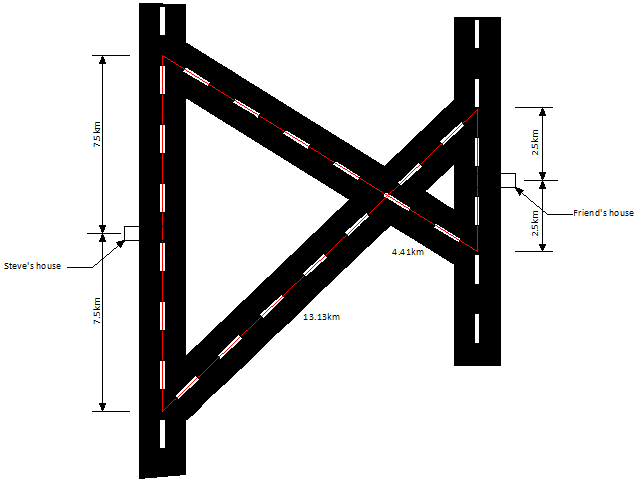
Пример №6: Стив хочет навестить своего приятеля, который недавно переехал в новый дом. Дорожная карта проезда к дому Стива и его приятеля вместе с известными Стиву расстояниями показана на рисунке. Помогите Стиву добраться к дому его приятеля наиболее коротким путем.
Решение:
Дорожную карту можно геометрически представить в следующем виде, как показано на рисунке.
Мы видим, что треугольники ΔABC и ΔCDE подобны, следовательно:
$frac = frac = frac$
В условии задачи сказано, что:
AB = 15 км, AC = 13.13 км, CD = 4.41 км и DE = 5 км
Используя эту информацию, мы можем вычислить следующие расстояния:
Стив может добраться к дому своего друга по следующим маршрутам:
A -> B -> C -> E -> G, суммарное расстояние равно 7.5+13.23+4.38+2.5=27.61 км
F -> B -> C -> D -> G, суммарное расстояние равно 7.5+13.23+4.41+2.5=27.64 км
F -> A -> C -> E -> G, суммарное расстояние равно 7.5+13.13+4.38+2.5=27.51 км
F -> A -> C -> D -> G, суммарное расстояние равно 7.5+13.13+4.41+2.5=27.54 км
Следовательно, маршрут №3 является наиболее коротким и может быть предложен Стиву.
Пример 7:
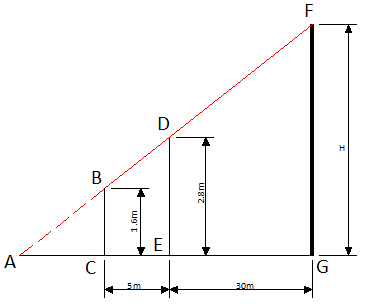
Триша хочет измерить высоту дома, но у нее нет нужных инструментов. Она заметила, что перед домом растет дерево и решила применить свою находчивость и знания геометрии, полученные в школе, для определения высоты здания. Она измерила расстояние от дерева до дома, результат составил 30 м. Затем она встала перед деревом и начала отходить назад, пока верхний край здания стал виден над верхушкой дерева. Триша отметила это место и измерила расстояние от него до дерева. Это расстояние составило 5 м.
Высота дерева равна 2.8 м, а высота уровня глаз Триши равна 1.6 м. Помогите Трише определить высоту здания.
Решение:
Геометрическое представление задачи показано на рисунке.
Сначала мы используем подобность треугольников ΔABC и ΔADE.
$frac = frac = frac = frac Rightarrow 2.8 times AC = 1.6 times (5 + AC) = 8 + 1.6 times AC$
$(2.8 — 1.6) times AC = 8 Rightarrow AC = frac = 6.67$
Затем мы можем использовать подобность треугольников ΔACB и ΔAFG или ΔADE и ΔAFG. Давайте выберем первый вариант.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Задачи наподобие треугольников с ответами
Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Заметим, что высота экрана, расположенного на расстоянии 250 см, в 2 раза меньше высоты экрана, расположенного на искомом расстоянии, значит, по теореме о средней линии, искомое расстояние в два раза больше первоначального экрана: 250·2 = 500.
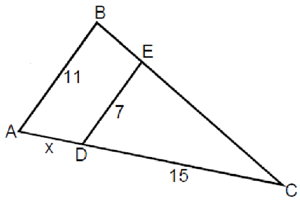
Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?
Столб и человек образуют два прямоугольных треугольниках ABC и FEB. Эти треугольники подобны по двум углам. Пусть высота фонаря равна тогда, поскольку расстояние от фонаря до конца тени равно 12 шагов, получаем:
откуда
Видео:Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Решение задач по теме «Подобие треугольников»
Представлены задачи по теме Подобие треугольников:
1) для самостоятельного решения; 2) с решениями; 3) из сборника ОГЭ; 4) тест.
Просмотр содержимого документа
«Решение задач по теме «Подобие треугольников»»
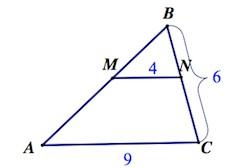
1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4, АС = 9.
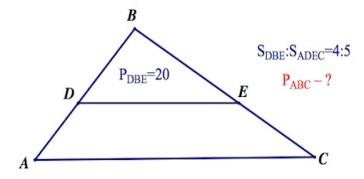
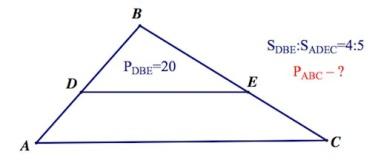
2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.
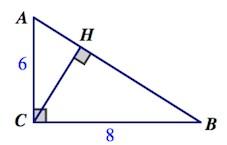
3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.
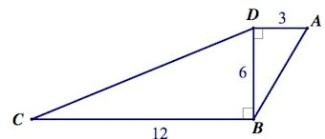
4. В трапеции ABCD меньшая диагональ BD, равная 6, перпендикулярна основаниям AD=3 и DC=12. Найдите сумму тупых углов B и D.
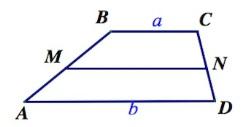
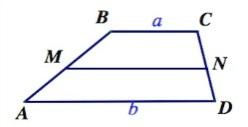
5. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.
1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4, АС = 9.
2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.
3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.
4. В трапеции ABCD меньшая диагональ BD, равная 6, перпендикулярна основаниям AD=3 и DC=12. Найдите сумму тупых углов B и D.
5. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.
Задачи для изучения (с решением):
Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.
Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить третий признак подобия треугольников:
Т.к. все отношения равны 3, то треугольники подобны
Третий признак подобия треугольников
Пример №2: Докажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR.
Первый признак подобия
Пример №3: Определите длину AB в данном треугольнике.
Первый признак подобия
Пример №4:Определить длину AD (x) геометрической фигуры на рисунке.
Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически.
AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC
Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны.
Следовательно:
x = AC — DC = 23,57 — 15 = 8,57
ТЕСТ
🎬 Видео
Подобные треугольникиСкачать

Решение задач на тему "Подобные треугольники". 8 классСкачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

8 класс, 20 урок, Определение подобных треугольниковСкачать

Геометрия . Задачи на подобие треугольников. Изи.Скачать

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ 8 класс ЗАДАЧИ коэффициент подобияСкачать

Подобные треугольники - 8 класс геометрияСкачать

Задача на подобие треугольников 1частьСкачать

Контрольная работа| Подобные треугольники | 8 класс | ГеометрияСкачать

Подобные треугольники Решение ЗадачСкачать

Задача 15 ОГЭ: подобные треугольники в трапецииСкачать

Сложная задача на подобие треугольников (видео 11)| Подобие. Геометрия | МатематикаСкачать

ОГЭ по математике. Задание 15. Все задачи на подобные треугольники.Скачать

Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать

Найти высоту дерева Задача на подобие треугольников 2 частьСкачать