Векторы в технической механике

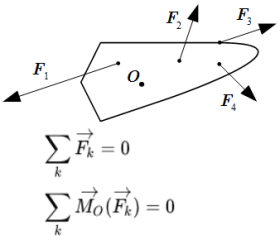
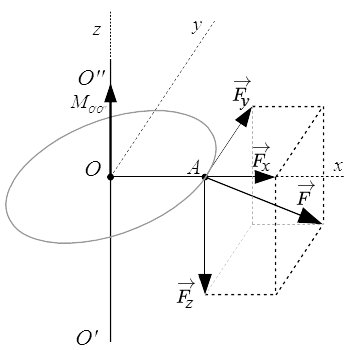
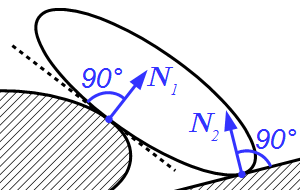
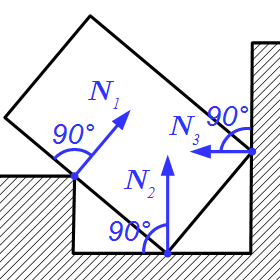
§1. Элементы векторной алгебры

В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.

1. Понятие вектора.

Вектор — это направленный отрезок, который характеризуется длиной и направлением.

Операции над векторами. Вектора можно складывать и умножать на число.

— сумма двух векторов есть вектор

α∙ — произведение вектора на действительное число есть вектор

— существует нулевой вектор

Рис.1. Сложение векторов

В математике все вектора являются свободными, их можно переносить параллельно самим себе.

В сумме двух векторов (рис.1,а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (рис.1,б) получаем, что суммой нескольких векторов является вектор замыкающий ломаную линию, состоящую из слагаемых векторов.

Операции над векторами подчиняются следующим законам (см. рис.2):

Рис.2. Операции над векторами

2. Проекцией вектора на ось

Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону (см. рис.3).

Рис.3. Проекция вектора на ось

§2. Основные понятия статики

Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.

Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не де­формируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.

Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.

1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.

В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН). Сила является величиной векторной.

Ее действие на тело опре­деляется:

1) численной величиной или модулем силы

2) направле­нием силы

3) точкой приложения силы (рис.4).

Рис.4. Сила, приложенная к телу

Например, будем прикладывать к стулу одну и ту же по модулю силу F. При приложении силы сверху вниз стул остается в состоянии покоя; при положении силы снизу вверх — стул поднимается; изменим направление нагружения, приложим силу горизонтально к спинке стула — стул опрокинется. Так как во всех случаях направление и место приложения силы различны, то и результат действия силы на стул разный, несмотря на то, что модуль силы F во всех случаях одинаков.

Силу, как и другие векторные величины, изображают в виде направленного отрезка со стрелкой на конце, указывающей его направление.

Прямая DE, вдоль которой направлена сила, называется линией действия силы.

Понятия «линия действия» и «направление» близки, но не тождественны. Очевидно, что по линии действия можно определить направление с точностью до противоположного. Аналогично связаны понятия «модуль» и «величина» для вектора.

В тексте вектор силы обозначается ла­тинскими буквами и др., с черточками над ними. Если черточки нет, значит у силы известна только ее чис­ленная величина — модуль.

2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил. Предполагается, что действие силы на тело не изменится, если ее перене­сти по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие ее на тело будет совсем другим.

3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, на­зывается свободным.

4. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состоя­ния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.

Например, если системы сил, изображенных на рис. 5, а и рис. 5, б, уравновешены, то эти две системы сил будут эквивалентны друг другу.

Рис 5. Система сил:

а – заданная система сил; б – эквивалентная система сил

5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или экви­валентной нулю.

6. Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Таким образом, равнодействующая — это сила, которая одна заменяет действие данной системы сил на твердое тело. Так как система сил F₁ и F₂ эквивалентна одной силе R (рис. 5, б), то сила R называется равнодействующей данной системы сил. Силы F₁ и F₂ в свою очередь могут называться составляющими силы R.

7. Сила, равная равнодействующей по модулю, прямо противополож­ная ей по направлению и действующая вдоль той же прямой, назы­вается уравновешивающей силой.

8. Силы, действующие на твердое тело, можно разделить на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.

9. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной.

Силы, действующие на все точки дан­ного объема или данной части поверхности тела, называются распре­деленными.

Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, пред­ставляют собою по существу равнодействующие некоторых систем распределенных сил.

В частности, обычно рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собою равно­действующую сил тяжести его частиц. Линия действия этой равно­действующей проходит через точку, называемую центром тяжести тела.

§3. Аксиомы статики

Все теоремы и уравнения статики выво­дятся из нескольких исходных положений, принимаемых без матема­тических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.

Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F₁ = F₂) и направлены вдоль одной прямой в противоположные стороны (рис. 6).

Рис.6. Система сил, находящаяся в равновесии

Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равнове­сии не может.

Аксиома 2. Действие данной си­стемы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

Эта аксиома устанавливает, что две системы сил, отличающиеся на уравнове­шенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсо­лютно твердое тело не изменится, если перенести точку при­ложения силы вдоль ее линии действия в любую другую точку тела.

Рис.7. Система сил

В самом деле, пусть на твердое тело действует приложенная в точке А сила (рис.7). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы

и , такие, что , . От этого действие силы на тело не изменится. Но силы и со­гласно аксиоме 1 также образуют уравновешенную систему, которая может быть отброшена. В резуль­тате на тело. Будет действовать только одна сила

, равная , но приложен­ная в точке В.

Таким образом, вектор, изобра­жающий силу , можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим).

Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю па­раллелограмма, построенного на этих силах, как на сторонах.

Вектор , равный диагонали параллелограмма, построенного на векторах и (рис.8), называется геометрической суммой векторов и : .

Рис.8. Равнодействующая двух сил

Величина равнодействующей . Если векторы сил окажутся перпендикулярными, то

Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействую­щую, равную геометрической (векторной) сумме этих сил и прило­женную в той же точке.

Аксиома 4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но проти­воположное по направлению противодействие.

Закон о равенстве действия и противодей­ствия является одним из основных законов ме­ханики. Из него следует, что если тело А дей­ствует на тело В с силой , то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но противоположную сторону силой

(рис. 9). Однако силы и не образуют урав­новешенной системы сил, так как они приложены к разным телам. Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме 4 рассматривается случай, когда силы приложены к разным телам и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме 2.

Рис.9. Противодействие

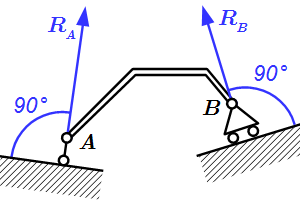
Этот принцип утверждает, что в природе не существует односторонних явлений. На рис. 10 изображена балка, опирающаяся на стены концами А и В. Для выявления сил действия и противодействия отделим балку от стен. Тогда силы действия балки на стену выражаются силами D_A и D_B, приложенными к стенам, а силы противодействия — силами R_A и R_B, приложенными к балке, которые в дальнейшем будем называть реакциями.

Рис. 10. Опирание балки на опоры:

а – схема загружения балки; б – силы действия балки на

опоры и противодействия со стороны опор на балку

Аксиома 5 (принцип отвердевания). Равновесие изме­няемого (деформируемого) тела, находящегося под действием дан­ной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сва­ренными друг с другом и т. д.

Аксиома 6 (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).

Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.

Видео-урок «Аксиомы статики»

§4. Связи и их реакции

По определению, тело, которое не скреплено с другими телами и может совершать из данного положе­ния любые перемещения в пространстве, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью.

Например, тело лежащее на столе – несвободное тело. Связью его является плоскость стола, которая препятствует перемещению тела вниз.

Очень важен так называемый принцип освобождаемости, которым будем пользоваться в дальнейшем. Записывается он так:

Любое несвободное тело можно сделать свободным, если связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.

Сила, с которой данная связь действует на тело, препятствуя тем ила иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.

Так у тела, лежащего на столе, связь – стол. Тело несвободное. Сделаем его свободным – стол уберем, а чтобы тело осталось в равнове­сии, заменим стол силой, направленной вверх и равной, конечно, весу тела.

Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь одновременно препятствует перемещениям тела по нескольким направлениям, направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.

Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим силам.

Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровые нагрузки и т.п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.

Одна из главных задач статики твердого тела — нахождение реакции связей. Для определения реакции связей необходимо найти величину этой реакции, линию и направление ее действия. Линия действия реакции обычно проходит через точку касания тела и связи. Численное значение реакции определяется расчетом, а направление реакции зависит от вида (конструкции) связи.

Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.

Рассмотрим, как направлены реакции некоторых основных видов связей:

1. Гладкая плоскость (поверхность) или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпен­дикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис.11, а). Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям сопри­касающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис. 11, б), то реакция направлена по нормали к другой поверх­ности.

Видео:Построение проекции вектора на осьСкачать

Теоретическая механика. В помощь студенту

Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.

Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.

Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.

Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Статика твердого тела

Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.

Основные понятия и законы статики

Эквивалентные системы сил – это такие системы сил, замена которых одна на другую не изменяет механического состояния тела.
Принятое обозначение: .

Уравновешенная система сил – это система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия).
.

Равнодействующая сила – это сила, действие которой на тело эквивалентно действию системы сил.
.

Пара сил – это система двух параллельных равных по модулю противоположно направленных сил.
Принятое обозначение: .
Под действием пары сил тело будет совершать вращательное движение.

Закон 4. Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке, равна по модулю диагонали параллелограмма, построенного на этих силах, и направлена вдоль этой
диагонали.
По модулю равнодействующая равна:

Связи и их реакции
• Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности.
• Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры.
• Шарнирная неподвижная опора противодействует любому перемещению в плоскости, перпендикулярной оси вращения.
• Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня.
• Глухая заделка противодействует любому перемещению и вращению в плоскости. Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.

Момент силы относительно точки
• Абсолютное значение момента равно произведению модуля силы на кратчайшее расстояние h от центра вращения до линии действия силы. Расстояние h называют плечом силы.
  
• Момент считают положительным, если сила стремится вращать плечо h против хода часовой стрелки и отрицательным при вращении по ходу часовой стрелки.
• Свойства момента силы относительно точки:
  1) Момент силы не изменится при переносе точки приложения силы вдоль линии действия силы.
  2) Момент силы равен нулю, если линия действия силы проходит через точку приложения силы.
  3) Момент равнодействующей силы относительно точки равен сумме моментов слагаемых сил относительно этой точки.
  ,
  где

Момент силы относительно оси
• Момент силы относительно оси — это момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
  Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.
  
• Чтобы найти момент силы относительно оси, нужно:
  1) Провести плоскость перпендикулярную оси z.
  2) Спроецировать силу на эту плоскость и вычислить величину проекции .
  3) Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силы и вычислить его длину.
  4) Найти произведение этого плеча и проекции силы с соответствующим знаком.
• Свойства момента силы относительно оси.
  Момент силы относительно оси равен нулю, если:
  1) , то есть сила параллельна оси.
  2) h=0, то есть линия действия силы пересекает ось.

Момент пары сил
• Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (пара сил оказывает на тело вращающее действие)
  ,
  где: — силы, составляющие пару;
  h — плечо пары.
  Момент пары считают положительным, если силы стремятся вращать плечо против хода часовой стрелки.
• Свойства пары сил.
  1) Сумма проекций сил пары на любую ось равна нулю.
  2) Не изменяя момента пары можно одновременно соответственно изменять значение сил и плечо пары.
  3) Пару можно переносить в плоскости ее действия при этом действие пары на тело не изменится.

Преобразование сходящейся системы сил
• Равнодействующая двух сходящихся сил находится на основании аксиомы о параллелограмме сил.
  Геометрическая сумма любого числа сходящихся сил может быть определена путем последовательного сложения двух сил – способ векторного многоугольника.
  Вывод: система сходящихся сил () приводится к одной равнодействующей силе .
• Аналитически равнодействующая сила может быть определена через ее проекции на оси координат:
  
  Согласно теореме: проекция равнодействующей на ось равна сумме проекций слагаемых сил на эту ось: , или в общем виде
  С учетом равнодействующая определяется выражением:
  .
• Направление вектора равнодействующей определяется косинусами углов между вектором и осями x, y, z:
  

Преобразование произвольной системы сил
• Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится.
  В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов — суммарным моментом.
  Суммарный вектор — это главный вектор системы сил.
  Суммарный момент — это главный момент системы сил.
  Вывод: произвольная система сил в результате тождественного преобразования приводится к главному вектору и главному моменту системы сил.
• Аналитически главный вектор и главный момент системы сил могут быть определены через их проекции на оси координат:
  ,
  

Условия равновесия систем сил
• Равновесие системы сходящихся сил
  Действие системы сходящихся сил эквивалентно действию одной равнодействующей силы.
  Для равновесия тела необходимо и достаточно, чтобы равнодействующая равнялась нулю .
  Из формулы следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю:
  
• Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y равнялась нулю:
  

Равновесие произвольной системы сил.
• Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия необходимо и достаточно выполнения условия:
  .
• Для равновесия произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси X,Y,Z и суммы моментов всех сил относительно осей X,Y,Z равнялись нулю:
  
• Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций главного вектора на оси X,Y, и алгебраическая сумма моментов сил относительно центра О были равны нулю:
  

Видео:Физика | Ликбез по векторамСкачать

Кинематика

Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.

Основные понятия кинематики

Способы задания движения точки
• Задать движение точки — значит задать изменение ее положения по отношению к выбранной системе отсчета. Существуют три основные системы отсчета: векторная, координатная, естественная.
• В векторной системе положение точки относительно начала отсчета задается радиус-вектором.
  Закон движения: .
• В системе координат OXYZ положение точки задается тремя координатами X, Y, Z.
  Закон движения: x = x(t), y = y(t); z = z(t).
• В естественной системе отсчета положение точки задается расстоянием S от начала отсчета до этой точки вдоль траектории.
  Закон движения: .
  Движение точки, при естественном способе задания движения, определено если известны:
  1) Траектория движения.
  2) Начало и направление отсчета дуговой координаты.
  3) Уравнение движения.
  При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются:
  Касательная (τ) – направлена в сторону возрастания дуговой координаты по касательной к траектории.
  Главная нормаль (n) – направлена в сторону вогнутости кривой.
  Бинормаль (b) – направлена перпендикулярно к осям τ, n.

Определение кинематических характеристик точки
• Траектория точки
  В векторной системе отсчета траектория описывается выражением: .
  В координатной системе отсчета траектория определяется по закону движения точки и описывается выражениями z = f(x,y) — в пространстве, или y = f(x) – в плоскости.
  В естественной системе отсчета траектория задается заранее.
• Определение скорости точки в векторной системе координат
  При задании движения точки в векторной системе координат отношение перемещения к интервалу времени называют средним значением скорости на этом интервале времени: .
  Принимая интервал времени бесконечно малой величиной, получают значение скорости в данный момент времени (мгновенное значение скорости): .
  Вектор средней скорости направлен вдоль вектора в сторону движения точки, вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки.
  Вывод:скорость точки – векторная величина, равная производной от закона движения по времени.
  Свойство производной:производная от какой либо величины по времени определяет скорость изменения этой величины.
• Определение скорости точки в координатной системе отсчета
  Скорости изменения координат точки:
  .
  Модуль полной скорости точки при прямоугольной системе координат будет равен:
  .
  Направление вектора скорости определяется косинусами направляющих углов:
  ,
  где — углы между вектором скорости и осями координат.
• Определение скорости точки в естественной системе отсчета
  Скорость точки в естественной системе отсчета определяется как производная от закона движения точки: .
  Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях определяется только одной проекцией .

Ускорение точки
• По определению ускорение характеризует изменение скорости, то есть скорость изменения скорости.
• Ускорения точки в векторной системе отсчета
  На основании свойства производной:
  .
  Вектор скорости может изменяться по модулю и направлению.
  Вектор ускорения направлен по линии приращения вектора скорости, т. е. в сторону искривления траектории.
• Ускорение точки в координатной системе отсчета
  Ускорение изменения координат точки равно производной по времени от скоростей изменения этих координат:
  .
  Полное ускорение в прямоугольной системе координат будет определяться выражением:
  .
  Направляющие косинусы вектора ускорения:
  .
• Ускорение точки в естественной системе отсчета Приращение вектора скорости можно разложить на составляющие, параллельные осям естественной системы координат:
  .
  Разделив левую и правую части равенства на dt, получим:
  ,
  где — тангенциальное ускорение;
  — нормальное ускорение;
  R — радиус кривизны траектории в окрестности точки.

Кинематика твердого тела
• В кинематике твердых тел решаются две основные задачи:
  1) задание движения и определение кинематических характеристик тела в целом;
  2) определение кинематических характеристик точек тела.
• Поступательное движение твердого тела
  Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.
  Теорема:при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.
  Вывод:поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.
• Вращательное движение твердого тела вокруг неподвижной оси
  Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
  Положение тела определяется углом поворота . Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
  Закон вращательного движения тела вокруг неподвижной оси .
  Угловую скорость и угловое ускорение тела определим методом дифференцирования:
  — угловая скорость, рад/с;
  — угловое ускорение, рад/с².
  Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М, то точка М будет описывать вокруг точки С окружность радиуса R. За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние .
  Модуль линейной скорости:
  .
  Ускорение точки М при известной траектории определяется по его составляющим :
  ,
  где .
  В итоге, получаем формулы
  тангенциальное ускорение: ;
  нормальное ускорение: .

Плоско-параллельное движение твердого тела
• Плоско-параллельное движение твердого тела — это движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных одной неподвижной плоскости.
  Движение сечения S в своей плоскости можно рассматривать как сложное, состоящее из двух элементарных движений:
  1) поступательного и вращательного;
  2) вращательного относительно подвижного (мгновенного) центра.
• В первом варианте движение сечения может быть задано уравнениями движения одной его точки (полюса) и вращением сечения вокруг полюса.
  В качестве полюса может быть принята любая точка сечения.
  Уравнения движения запишутся в виде:
  .
  Ускорение точки движущейся плоской фигуры складывается из ускорения полюса относительно неподвижной системы отсчета и ускорения за счет вращательного движения вокруг полюса.
  
  
• Во втором варианте движение сечения рассматривается как вращательное вокруг подвижного (мгновенного) центра P.
  В этом случае скорость любой точки В сечения будет определяться по формуле для вращательного движения:
  .
  Угловая скорость вокруг мгновенного центра Р может быть определена если известна скорость какой либо точки сечения, например точки А.
  .
• Положение мгновенного центра вращения может быть определено на основании следующих свойств:
  1) вектор скорости точки перпендикулярен радиусу;
  2) модуль скорости точки пропорционален расстоянию от точки до центра вращения ();
  3) скорость в центре вращения равна нулю.
• Теорема:проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки, равны между собой и одинаково направлены.
  Доказательство: расстояние АВ изменяться не может, следовательно, не может быть больше или меньше .
  Вывод:.

Сложное движение точки
• Относительное движение — это движение точки относительно подвижной системы.
  Переносное движение — это движение точки вместе с подвижной системой.
  Абсолютное движение — это движение точки относительно неподвижной системы.
  Соответственно называют скорости и ускорения:
  — относительные;
  — переносные;
  — абсолютные.
• Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей (согласно теореме о сложении скоростей):
  .
  Абсолютное значение скорости определяется по теореме косинусов:
  .
• Ускорение по правилу параллелограмма определяется только при поступательном переносном движении
  .
  .
• При непоступательном переносном движении появляется третья составляющая ускорения, называемое поворотным или кориолисовым.
  ,
  где .
  Кориолисово ускорение численно равно:
  ,
  где – угол между векторами и .
  Направление вектора кориолисова ускорения удобно определять по правилу Н.Е. Жуковского: вектор спроектировать на плоскость, перпендикулярную оси переносного вращения, проекцию повернуть на 90 градусов в сторону переносного вращения. Полученное направление будет соответствовать направлению кориолисова ускорения.

Видео:Как решить любую задачу по механике. АлгоритмСкачать

Динамика

Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.

Основные понятия динамики

Центр масс механической системы — геометрическая точка, координаты которой определяются формулами:

где m_k, x_k, y_k, z_k — масса и координаты k-той точки механической системы, m — масса системы.
В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.

Момент инерции материального тела относительно оси – это количественная мера инертности при вращательном движении.
Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси:
.
Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек:

Сила инерции материальной точки — это векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения:

Сила инерции материального тела — это векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс: ,
где — ускорение центра масс тела.

Элементарный импульс силы — это векторная величина , равная произведению вектора силы на бесконечно малый промежуток времени dt:
.
Полный импульс силы за Δt равен интегралу от элементарных импульсов:
.

Элементарная работа силы — это скалярная величина dA, равная скалярному произведению вектора силы на бесконечно малое перемещение .
Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов:
,
где α — угол между направлениями векторов перемещения и силы.

Работа силы на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению:
.
Единица измерения работы — Джоуль (1 Дж = 1 Н·м).

Количество движения материальной точки — это векторная величина , равная произведению массы m на её скорость :
.

Количество движения механической системы равно векторной сумме количества движения её точек.
или
,
где m — масса механической системы, — вектор скорости центра масс системы.

Кинетическая энергия материальной точки — это скалярная величина Т, равная половине произведения массы точки на квадрат её скорости:
.

Кинетическая энергия механической системы равна сумме кинетических энергий всех её точек:
.

Аксиомы динамики
• Первая аксиома — это закон инерции.
  Если на свободную материальную точку не действуют никакие силы или действует уравновешенная система сил, то точка будет находиться в состоянии покоя или равномерного прямолинейного движения.
• Вторая аксиома — закон пропорциональности ускорения.
  Ускорение, сообщаемое материальной точке действующей на неё силой, пропорционально этой силе и по направлению совпадает с направлением силы: — это основной закон динамики.
• Третья аксиома — это закон противодействия.
  Силы, с которыми действуют друг на друга две материальные точки, равны по модулю и направлены вдоль прямой, соединяющей эти точки, в противоположные стороны:
  .
• Четвертая аксиома — закон независимости действия сил.
  При действии на материальную точку системы сил полное ускорение этой точки равно геометрической сумме ускорений от действия каждой силы:
  

Дифференциальные уравнения динамики
• Дифференциальные уравнения движения точки связывают ускорение точки с действующими на нее силами. Фактически дифференциальные уравнения являются записью основного закона динамики в явной дифференциальной форме.
  Для абсолютного движения точки (движение в инерциальной системе отсчета) дифференциальное уравнение имеет вид:
  .
• Векторное уравнение может быть записано в проекциях на оси прямоугольной инерциальной системы координат:
  
• При известной траектория движения точки уравнение может быть записано в проекциях на оси естественной системы координат:
  
  С учетом того, что ,
  где — тангенциальное ускорение;
  — нормальное ускорение,
  уравнения примут вид:
  

Общие теоремы динамики
• Общие теоремы динамики устанавливают зависимость между мерами механического движения и механического взаимодействия. Выводы теорем являются результатом тождественного преобразования основного закона динамики.
• Теорема об изменении количества движения: изменение количества движения материальной точки (механической системы) за конечный промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени — для материальной точки;
  — для механической системы.
• Теорема об изменении кинетической энергии: изменение кинетической энергии точки (механической системы) при её перемещении равно сумме работ всех действующих внешних сил на этом перемещении — для материальной точки;
  — для механической системы.
• Кинетическая энергия механической системы определяется в соответствии с , при этом для твердых тел выведены следующие зависимости:
  — при поступательном движении тела;
  — при вращательном движении тела;
  — при плоско-параллельном движении тела.
• Момент инерции цилиндра относительно его оси:
  .
• Момент инерции стержня относительно оси z:
  .
• Момент инерции прямоугольной пластины относительно осей х и y: .
• Момент инерции шара определяется по формуле:
  .
• Работа силы тяжести:
  ,
  где P — сила тяжести;
  h — изменение положения тела по вертикали.
• Работа силы при вращательном движении тела
  ,
  где M — момент силы,
  w — угловая скорость тела.
  Следует иметь в виду, что работа, как скалярная величина, может быть положительной или отрицательной. Работа будет положительной если направление действия силы совпадает с направлением движения.

Принцип Даламбера
• Формулировка принципа Даламбера: если в любой момент времени к действующим на точку силам присоединить силы инерции, то полученная система сил будет уравновешенной:
  .
• Для механической системы:
  .

Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Примеры решения задач

Решение примеров по теме: «Статика твердого тела»

Пример 1. Условия равновесия

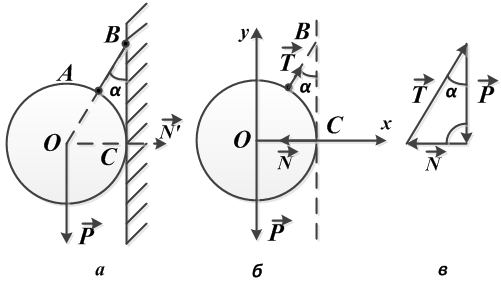
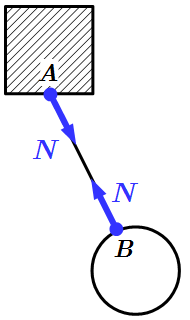
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.

Дано: P = 10 Н; α = 45°
Найти: N, T — ?

Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.

Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).

Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).

При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).

В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:

После подстановки в формулы числовых значений, получим:
.

Ответ: .

Решение примеров по теме: «Кинематика»

Пример 2. Уравнение траектории точки

Дано:
Движение точки задано уравнениями ;
(x, у — в сантиметрах, t — в секундах).
Найти: уравнение траектории точки в координатной форме.

Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
.

Опуская промежуточные выражения, получаем уравнение траектории:
.

Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).

Ответ: .

Решение примеров по теме: «Динамика»

Пример 3. Основной закон динамики точки

Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.

Дано: m = 10 кг; a = 0,5 м/с 2 .
Найти: F — ?

Решение.
Согласно основному закону динамики: .

Подставив значения в формулу, получим:

Ответ: сила, сообщающая массе, равной 10 кг,
ускорение 0,5 м/с 2 , равна 5 Н.

В помощь студенту

Формулы, правила, законы, теоремы, уравнения, примеры решения задач

Список литературы:
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.

Видео:ВекторыСкачать

Статика – раздел теоретической механики

Видео:Математика это не ИсламСкачать

Определение и роль статики в теоретической механике

Основной задачей статики является установление законов преобразования системы сил в эквивалентные системы. Методы статики применяются не только при изучении тел, находящихся в равновесии, но и в динамике твердого тела, при преобразовании сил в более простые эквивалентные системы.

Под состоянием равновесия, в статике, понимается состояние, при котором все части механической системы покоятся относительно некоторой инерциальной системы координат. Одним из базовых объектов статики являются силы и точки их приложения.

Видео:Техническая механикаСкачать

Понятие силы

Единицей измерения силы является один Ньютон:
.
В технике широко используется килоньютон:
.

Как следует из определения, сила – это векторная величина, которая, в трехмерном пространстве, имеет три проекции на оси координат. Также задать силу можно с помощью абсолютной величины (модуля) и направления. Для материальной точки, сила приложена к самой точке. Но если мы рассматриваем твердое тело, то кроме вектора силы нам нужно еще указать и точку ее приложения. Таким образом, действие силы на твердое тело характеризуется вектором силы и точкой ее приложения. Если выбрать систему отсчета, то действие силы на твердое тело определяется двумя векторами. Это вектор силы, и вектор, проведенный из начала системы отсчета в точку приложения силы.

Система сил, действующих на тело – это совокупность векторов сил, приложенных к телу, и точек их приложения.
Эквивалентные системы сил Две системы сил являются эквивалентными, если законы движения любых точек твердого тела совпадают при действии любой из этих систем.
Эквивалентное преобразование системы сил – это переход от одной системы сил к эквивалентной ей системе.
Система взаимно уравновешивающихся сил – это система сил, не меняющая уравнений движения или уравнений равновесия твердого тела. То есть это система, эквивалентная отсутствию сил.
Равнодействующая – это одна сила, действие которой эквивалентно действию данной системы сил.

Закрепленные, скользящие и свободные векторы

Поскольку действие силы на твердое тело определяется двумя векторами, то часто под силой подразумевают множество, состоящее из двух векторов – вектора силы, и вектора точки ее приложения относительно выбранной системы координат. Такие множества подразделяются на три класса, для которых вводят специальные термины.

Закрепленный вектор – это множество, состоящее из образующего вектора и точки его приложения. Два закрепленных вектора считаются равными только в том случае, если равны их образующие векторы и совпадают точки приложения. Закрепленный вектор также называют связанным или фиксированным вектором.
Скользящий вектор – это множество, состоящее из образующего вектора и точки его приложения, обладающее тем свойством, что точку приложения можно перемещать вдоль прямой, параллельно образующему вектору. То есть два скользящих вектора считаются равными, если равны образующие векторы и точки их приложения расположены на одной прямой, параллельной образующему вектору.
Свободный вектор – это множество, состоящее из образующего вектора и точки его приложения. Два свободных вектора считаются равными, если равны образующие векторы, не зависимо от точек приложения.
Линия действия силы – это прямая, проведенная через точку приложения силы параллельно ее направлению.

Если мы рассматриваем упругое тело, то сила – это закрепленный вектор. Деформации зависят не только от величин и направлений сил, но и от точек их приложения. Если мы рассматриваем движение или равновесие абсолютно твердого тела, то действующая сила является скользящим вектором. Перемещение ее точки приложения вдоль линии ее действия не меняет уравнений движения или уравнений равновесия. Угловая скорость вращения абсолютно твердого тела является свободным вектором. Она характеризует движение в целом, и ее значение одинаково во всех точках тела.

С математической точки зрения, статика – это алгебра скользящих векторов.

Проекции силы на оси координат

Сила в трехмерном пространстве

Пусть у нас есть декартова система координат Oxyz . И пусть – единичные векторы, направленные вдоль ее осей , и , соответственно. Пусть – проекции вектора силы на оси координат. Тогда разложение силы на составляющие вдоль координатных осей имеет вид:
.
Абсолютное значение (модуль) силы:
.

Введем единичный вектор , направленный вдоль вектора силы . Тогда
.
Эта формула выражает тот факт, что вектор силы можно задать, указав ее модуль F и направление . Вектор имеет три проекции на оси координат: . Поскольку его длина равна единице: , то они связаны соотношением:
.
То есть единичный вектор имеет только две независимые компоненты. Таким образом, для задания вектора силы нужно знать три величины:
либо три проекции на оси координат ;
либо модуль F и направление , которое задается двумя независимыми величинами.

Введем углы между вектором силы и осями координат , и . Тогда проекции силы на оси координат определяются по формулам:
;
.
Косинусы углов называются направляющими косинусами.

Направляющие косинусы вектора – это косинусы углов между вектором и осями координат. Они являются проекциями единичного вектора , сонаправленного с :
,
и связаны соотношением:
.

Сила на плоскости

Результаты, приведенные выше, можно применить и для плоской декартовой системы координат Oxy . В этом случае имеем:
;
;
;
;
;
;
.
Поскольку , то . Последнее уравнение представляет собой известную тригонометрическую формулу:
.
Для задания вектора силы , необходимо знать две независимые величины:
либо проекции вектора на оси координат ;
либо модуль F и направление , которое задается одним углом .

Видео:Определение реакций опор в балке. Сопромат.Скачать

Аксиомы статики

Часть аксиом являются основными законами механики. Другая часть относится к законам преобразования сил, действующих на абсолютно твердое тело, и применяется только к задачам теоретической механики. По своей сути, они выражают собой тот факт, что действие силы на тело является скользящим вектором.

1. Аксиома инерции (закон инерции Галилея)
Существуют такие системы отсчета, в которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если тело покоилось в определенный момент времени, то оно будет покоиться и в последующие моменты.

Такие системы отсчета называются инерциальными. В механике, если это особо не оговорено, под системой отсчета подразумевается именно инерциальная система отсчета. Аксиому инерции иногда формулируют так.

1′. Аксиома инерции
В инерциальной системе отсчета, под действием взаимно уравновешивающихся сил, материальная точка находится в состоянии покоя или движется прямолинейно и равномерно, а первоначально покоившееся тело продолжает покоиться и в последующие моменты времени.

2. Аксиома равновесия двух сил
Две силы, приложенные к абсолютно твердому телу, являются уравновешенными тогда и только тогда, когда они равны по модулю, направлены в противоположные стороны и их линии действия совпадают.

3. Аксиома присоединения и исключения уравновешивающихся сил
Кинематическое состояние твердого тела не изменится, если к действующей на него системе сил прибавить или отнять уравновешенную систему сил.

То есть, прибавляя или исключая уравновешенную систему сил, мы получаем эквивалентную систему сил.

Следствие аксиом 2 и 3
Действие силы на твердое тело не изменится, если точку приложения силы перенести вдоль ее линии действия. То есть сила, приложенная к твердому телу, является скользящим вектором. Доказательство

4. Аксиома параллелограмма сил
Две силы, приложенные к телу в одной точке, можно заменить их равнодействующей силой, равной векторной сумме этих сил и приложенной к той же точке.
Верно и обратное. Любую силу можно разложить на две (и более) силы по правилу векторной суммы (по правилу параллелограмма), приложенных в той же точке, что и исходная сила.

То есть, если силы и приложены в одной точке, то их можно заменить равнодействующей , приложенной к той же точке. Сумму векторов можно найти двумя способами.
1) Можно вычислить проекции сил на оси прямоугольной системы координат:
.

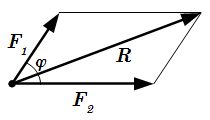
Сложение сил по правилу параллелограмма

2) Можно сложить векторы по правилу параллелограмма (см. рисунок).
;
.
Здесь – угол между векторами и . Точкой обозначено скалярное произведение векторов.

5. Аксиома равенства действия и противодействия (3-й закон Ньютона)
Всякому действию соответствует равное и противоположно направленное противодействие.

То есть если мы возьмем все силы, действующие на тело 2 со стороны тела 1, и объединим их с силами, действующими на тело 1 со стороны тела 2, то получим уравновешенную систему сил.

6. Принцип отвердевания
Если деформируемое тело находится в равновесии, то его равновесие не нарушится, если тело считать абсолютно твердым.

Видео:Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

Система сходящихся сил

Система сходящихся сил всегда имеет равнодействующую , равную векторной сумме этих сил:
,
и приложена в точке их пересечения.

Таким образом, проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на оси координат:
;
.

Условия равновесия системы сходящихся сил
Если тело или система тел, на которые действует сходящаяся система сил, находится в покое, то равнодействующая этих сил равна нулю:
.
Это дает три уравнения равновесия:
.

Теорема о трех непараллельных силах
Если твердое тело находится в равновесии под действием трех сил, линии действия двух из которых пересекаются в одной точке, то все силы лежат в одной плоскости и являются сходящимися.

Следствие
Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то эти силы являются сходящимися.

Видео:Физика. 9 класс. Векторы в механикеСкачать

Параллельные силы

Ранее мы отмечали, что система сходящихся сил имеет равнодействующую. То есть такую систему можно заменить одной силой. Приведем еще важные примеры систем сил, имеющих равнодействующую.

Две силы одного направления

Пусть мы имеем две однонаправленные параллельные силы и . Переместим точки их приложения вдоль линий их действия в точки A и B так, чтобы отрезок AB был перпендикулярен силам. Тогда система сил и имеют равнодействующую , приложенную в точке C . Направление равнодействующей совпадает с направлениями и . Абсолютная величина равна сумме сил:
.
Точка приложения C находится между A и B и делит отрезок AB обратно пропорционально модулям сил:
.

Две противоположно направленные силы

Теперь рассмотрим противоположно направленные силы и , различающиеся по величине, . Пусть . Эта система также имеет равнодействующую , направление которой совпадает с направлением большей по модулю силы, а абсолютное значение равно абсолютному значению разности модулей сил:
.
Точка приложения C равнодействующей находится на продолжении отрезка AB , ближе к наибольшей по модулю силе . Расстояния до точек A и B также обратно пропорциональны и :
.

Видео:Момент силы относительно точки и осиСкачать

Момент силы относительно точки

Определение

Абсолютное значение момента силы относительно точки O равно произведению силы на плечо этой силы относительно выбранной точки O . Направление момента перпендикулярно плоскости, проходящей через точку O и линию действия силы.
Доказательство

Геометрическая интерпретация

Пусть векторы и расположены в плоскости рисунка. Согласно свойству векторного произведения, вектор перпендикулярен векторам и , то есть перпендикулярен плоскости рисунка. Его направление определяется правилом правого винта. На рисунке вектор момента направлен на нас. Пусть α – угол между векторами и . Абсолютное значение момента:
.

Из точки O проведем перпендикуляр OH к линии действия силы . Из прямоугольника OAH имеем: . Тогда
.
То есть абсолютное значение момента силы относительно точки O равно произведению силы F на плечо |OH| этой силы относительно точки O .

Компоненты момента силы в декартовой системе координат

Выберем декартову систему координат Oxyz с началом в точке O . Найдем компоненты вектора момента силы в этой системе координат относительно ее начала.

.
Здесь – единичные векторы в направлении осей ; – координаты точки A в выбранной системе координат: .

Таким образом, момент силы имеет следующие компоненты:
(М.1) ;
(М.2) ;
(М.3) .
Компоненты представляют собой значения момента силы относительно осей , соответственно.

Свойства момента силы относительно центра

Момент относительно центра O , от силы, проходящей через этот центр, равен нулю.
Доказательство

Если точку приложения силы переместить вдоль линии, проходящей через вектор силы, то момент, при таком перемещении, не изменится.
Доказательство

Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство

То же самое относится и к силам, чьи линии продолжения пересекаются в одной точке.

Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство

Теорема Вариньона о моменте равнодействующей
Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки равен векторной сумме моментов сил системы относительно той же точки.

Пара сил

Из предыдущих формул ⇑ видно, что если противоположно направленные силы имеют равные модули: , то система сил не имеет равнодействующей. Действительно, в этом случае . Пытаясь использовать предыдущие формулы, мы получим деление на нуль. Такую систему сил называют парой сил.

Пара сил – это система из двух сил , равных по абсолютной величине, имеющих противоположные направления, приложенных к разным точкам тела и не лежащих на одной прямой.
Плечо пары сил – это кратчайшее расстояние h между линиями действия сил, входящих в пару.
Момент пары сил – это векторная сумма моментов сил, входящих в пару, вычисленная относительно любой точки. Абсолютное значение момента пары равно произведению силы на плечо пары:
.

Теорема о независимости выбора центра при вычислении момента пары
Векторная сумма моментов сил, составляющих пару, не зависит от выбора точки, относительно которой вычисляются моменты.
Теорема об эквивалентности пар
Две пары, имеющие равные векторы моментов, эквивалентны. То есть у пары можно менять модуль силы и длину плеча, оставляя неизменным ее момент.
Теорема о возможности перемещения пары
Пару сил можно переносить в любом направлении. Другими словами, если пару сил переместить параллельным переносом в любое положение, то она будет эквивалентна исходной паре.
Теорема о сложении нескольких пар
Система нескольких пар сил эквивалентна одной паре, вектор момента которой равен векторной сумме моментов исходных пар.
Условие равновесия пар
Система, состоящая только из нескольких пар, является уравновешенной, если векторная сумма моментов пар равна нулю:
.

Видео:Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Момент силы относительно оси

Часто встречаются случаи, когда нам нужно знать не все компоненты момента силы относительно выбранной точки, а только проекцию момента на выбранное направление.

Момент силы относительно оси, проходящей через точку O – это проекция вектора момента силы относительно точки O , на направление оси.

Свойства момента силы относительно оси

Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство

Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство

Вычисление момента силы относительно оси

Пусть на тело, в точке A действует сила . Найдем момент этой силы относительно оси O′O′′ .

Построим прямоугольную систему координат. Направим ось z вдоль O′O′′ . Из точки A опустим перпендикуляр AO на O′O′′ . Через точки O и A проводим ось Ox . Перпендикулярно Ox и Oz проводим ось Oy . Разложим силу на составляющие вдоль осей системы координат:
.
Сила пересекает ось O′O′′ . Поэтому ее момент равен нулю. Сила параллельна оси O′O′′ . Поэтому ее момент также равен нулю. По формуле (М.3) находим:
.

Заметим, что компонента направлена по касательной к окружности, центром которой является точка O . Направление вектора определяется правилом правого винта.

Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Условия равновесия

Главный вектор и главный момент

Подчеркнем, что величина главного момента зависит от выбора центра, относительно которого вычисляются моменты.

Пространственная система сил

Основная форма условий равновесия

Условия равновесия системы сил
Для того, чтобы твердое тело под действием произвольной системы сил находилось в равновесии, необходимо и достаточно, чтобы главный вектор и главный момент, относительно произвольной точки C , равнялись нулю:
;
.
Здесь – точка приложения силы , .
Доказательство

Это основная форма условий равновесия. Точка C может, как принадлежать телу, так и находится за его пределами. Обычно центр C выбирают так, чтобы сделать вычисления более простыми. Спроектировав каждое из этих векторных уравнений на три направления, получим шесть уравнений, из которых можно определить шесть неизвестных величин.

Вторая форма условий равновесия

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и равнялась нулю, и чтобы сумма проекций сил на произвольное направление, не перпендикулярное направлению , равнялась нулю:
;
;
.
Доказательство

Третья форма условий равновесия

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и , не лежащих на одной прямой, равнялась нулю:
;
;
;
.
Доказательство

Плоская система сил

Все изложенное для пространственной системы сил является применимым и для плоской системы. Направим оси x и y декартовой системы координат в плоскости действия сил, а ось z – перпендикулярно. Тогда z компоненты координат точек и сил равны нулю: . Также равны нулю x, y компоненты моментов сил относительно произвольной точки C : . То есть момент может иметь отличное от нуля значение только для z компоненты. Поскольку z компонента не входит в плоскую систему координат xy , то, в двумерном пространстве, момент силы уже не является вектором, а является скаляром (точнее псевдоскаляром). Его называют алгебраическим моментом силы относительно центра C (или просто моментом силы относительно центра C ), и обозначают символом с маленькой буквы без знака вектора:
.

Величина является моментом силы относительно оси, проходящей через точку C перпендикулярно плоскости действия сил. Момент вычисляют как произведение модуля силы на плечо со знаком плюс или минус:
.
Если, при неподвижном центре C , сила стремится повернуть систему против часовой стрелки, то момент положителен . В противном случае – отрицательный: .

Величину момента от силы , приложенной в точке A , относительно центра C , также можно выразить через компоненты векторов по формуле:
,
где и – координаты точек A и C , соответственно.

Условия равновесия плоского тела

Для плоской системы сил можно составить три уравнения, из которых можно определить три неизвестных величины. Считаем, что сила приложена в точке .

Основная форма условий равновесия
;
;
.

Вторая форма условий равновесия
;
;
.

Третья форма условий равновесия
;
;
;
.

Связи и их реакции

Определения и свойства

Принцип освобождаемости
Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу.

Основные типы связей и их реакции

Плоские и пространственные задачи

Две гладкие не острые поверхности. Через точку соприкосновения проводим касательную плоскость к этим поверхностям. Реакция является силой, направленной перпендикулярно этой плоскости, то есть, направлена по нормали к обеим поверхностям в точке их соприкосновения.

Одна из гладких поверхностей является острием. Реакция является силой, направленной вдоль нормали не острой поверхности в точке соприкосновения.

Две шероховатые поверхности. То же самое, что и для гладких поверхностей, только в точке соприкосновения добавляем силу трения, лежащую в плоскости касания.

Невесомая нить и стержень. Реакция направлена вдоль нити или стержня. При этом на нить всегда действует сила растяжения. На стержень может действовать как растягивающая, так и сжимающая сила.

Плоские задачи

Следующие связи применяют только в плоских задачах.

Неподвижный шарнир. Реакция является силой, проходящей через ось шарнира. Обычно ее раскладывают на две составляющие параллельно осям координат.

Подвижный шарнир, или опора на катках. Реакция является силой, которая проходит через ось шарнира перпендикулярно опорной поверхности.

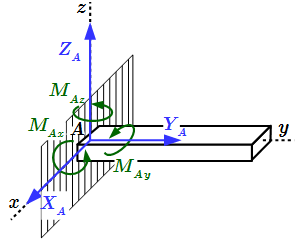
Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно оси, проходящей через точку соединения перпендикулярно плоскости фигуры. Силу обычно раскладывают на две составляющие параллельно осям координат.

Пространственные задачи

Цилиндрический шарнир или петля. Реакция является силой, проходящей через ось шарнира, перпендикулярно направлению оси. Обычно ее раскладывают на две составляющие параллельно осям координат.

Сферический подшипник или подпятник. Реакция является силой, проходящей через центр подшипника. Обычно ее раскладывают на три составляющие параллельно осям координат.

Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно этой точки. Силу и момент обычно раскладывают на три составляющие параллельно осям координат.

Силы трения

Трение скольжения

Рассмотрим тело, которое скользит по поверхности другого тела с отличной от нуля скоростью v под действием внешней силы . Если поверхности абсолютно гладкие, то в точках соприкосновения тел возникает только сила давления N , перпендикулярная плоскости соприкосновения тел. Для шероховатых поверхностей, возникает еще сила трения , параллельная плоскости соприкосновения, направленная в сторону, противоположную скорости движения. Величина силы трения пропорциональна силе давления и не зависит от площади соприкосновения поверхностей:
(Т1) .
Здесь f – безразмерный коэффициент, который называется динамическим коэффициентом трения, или коэффициентом трения скольжения. Он зависит от материалов и обработки соприкасаемых поверхностей и почти не зависит от скорости относительного движения. При расчетах его считают постоянной.

Сила трения скольжения – это сила трения, приложенная к точкам соприкосновения движущихся тел и параллельная плоскости их соприкосновения. То есть это сила, препятствующая скольжению одного тела по поверхности другого. При расчетах, под силой трения скольжения понимают равнодействующую всех сил трения, возникающих в точках соприкосновения тел.

Закон Амонта – Кулона
Сила трения скольжения направлена параллельно плоскости соприкосновения тел в сторону, противоположную их движению, которое возникло бы при отсутствии трения. Она не зависит от площади соприкосновения поверхностей, а зависит от силы давления N одной поверхности на другую, перпендикулярную плоскости соприкосновения тел:
.

Трение сцепления

Теперь рассмотрим статическую задачу. Пусть тело покоится, и на него действуют внешние силы с равнодействующей , приложенной под углом φ к нормали поверхности. Разложим ее на две составляющие: параллельную поверхности, и перпендикулярную . На тело также действуют сила реакции , перпендикулярная плоскости соприкосновения тел, и сила трения , которую при отсутствии скольжения называют силой сцепления. Сила сцепления направлена параллельно поверхности, препятствуя движению. Она может принимать значения от нуля до максимальной величины , определяемой аналогично (Т1):
(Т2) .
Здесь – статический коэффициент трения, который еще называют коэффициентом сцепления. Он не может быть меньше динамического коэффициента трения: .

Если , тело покоится. При этом сила трения сцепления меньше максимальной величины: . При , возникает движение. Когда , сила трения достигает предельной величины, возникает состояние предельного равновесия. Дальнейшее увеличение приводит к потере равновесия.

Сила трения сцепления – это сила трения скольжения, когда относительное перемещение соприкасающихся тел отсутствует.
Предельная сила трения – это максимальное значение силы трения сцепления.
Предельное равновесие – это состояние равновесия, при котором значение силы трения сцепления равно ее максимальному значению.

Из условий равновесия имеем: . Подставим в (Т2):
.
Отсюда получаем, что система будет находиться в равновесии, если
.
Видно, что условие равновесия зависит от угла φ , под которым приложена равнодействующая внешних сил, и не зависит от ее величины. Введем предельный угол трения: . Эту величину также называют просто углом трения. Тогда, условие равновесия можно записать так:
.
Это неравенство определяет конус в пространстве, который называется предельным конусом трения, конусом трения, или конусом сцепления. Если направление силы выходит за пределы этого конуса, то система начинает движение. Если направление силы попадает в конус сцепления, то система остается в состоянии покоя. Такое явление называется заклиниванием механизма.

Заклинивание механизма – это явление в механике, при котором система остается в состоянии покоя при любом, сколь угодно большом увеличении модуля внешней силы.

Условие возникновения движения при наличии трения
Для того чтобы тело начало движение, необходимо и достаточно, чтобы равнодействующая внешних сил находилась вне конуса трения.

Трение качения

Рассмотрим случай, когда одно из тел круглой формы катится без проскальзывания по поверхности другого. С точки зрения механики, такие тела соприкасаются в одной точке A . Площадь их соприкосновения бесконечно мала, в результате чего возникает бесконечно большое давление, которое не могут выдержать реальные материалы. Поэтому вблизи точки соприкосновения тел возникает деформация, которая имеет место только в небольшом участке соприкасающихся тел. В основной части тел, удаленных от точек соприкосновения, деформация практически отсутствует, и их можно рассматривать как абсолютно твердые тела. Тогда систему сил, возникающую в результате соприкосновения, можно привести к некоторой равнодействующей силе . При этом оказывается, что точка ее приложения смещена относительно оси симметрии катящегося тела. Это приводит к появлению момента сил относительно точки A , расположенной на оси симметрии круглого тела. Изучение деформированного состояния выходит за рамки теоретической механики. Поэтому мы приводим лишь результаты, применяемые в расчетах.

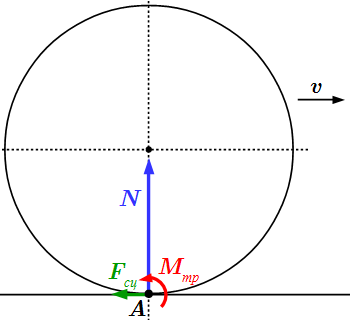
Расчетная схема трения качения.

1. Поскольку деформации, для небольших значений внешних сил малы, то, считают, что они не влияют на геометрические характеристики тел. То есть считают, что тела округлой формы соприкасаются в одной точке.
2. В точке соприкосновения, на тело действуют:
сила давления , перпендикулярная соприкасающимся поверхностям;
сила сцепления , лежащая в касательной плоскости, проходящей через точку соприкосновения поверхностей;
момент силы трения , препятствующий движению.
Максимальное значение момента силы трения определяется по формуле:
,
где δ – коэффициент трения качения, который имеет размерность длины.
3. Коэффициент трения качения зависит от соприкасающихся материалов и состояния их поверхностей. Он не зависит от кривизны поверхностей и угловой скорости вращения тела. А при движении с проскальзыванием, не зависит от скорости скольжения.

Центр тяжести тела

Центр тяжести в пространстве

Пусть тело состоит из n материальных точек. И пусть на каждую точку B_i действует сила тяжести , . Все силы тяжести, действующие на точки, параллельны. Поэтому мы имеем дело с параллельной системой сил. Как и для системы из двух однонаправленных сил, такая система сил имеет равнодействующую. Найдем ее.

Пусть – главный вектор. Поскольку все силы имеют одинаковое направление, то введем единичный вектор , направленный вдоль сил:
. Отсюда .

Найдем момент сил тяжести относительно произвольно расположенного центра O .
,
где
(ЦТ1) .

Отсюда видно, что формула вычисления момента имеет вид формулы момента от одной силы , приложенной в точке C . Точка C , положение которой определяется формулой (ЦТ1), называется центром тяжести тела. Таким образом, равнодействующая отдельных сил тяжести точек тела равна главному вектору силы тяжести, приложенному в центре тяжести. Модуль P равнодействующей называют весом тела.

Если бы мы находили равнодействующую сил тяжести, выполняя эквивалентные преобразования сил, то мы бы нашли только линию действия равнодействующей. Далее, если повернуть тело на некоторый угол, то можно найти другую линию действия равнодействующей. При этом все, подобным образом построенные линии, пересекаются в одной точке, которая и является центром тяжести тела.

Центр тяжести твердого тела – это точка, связанная с телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела, при любом положении тела в пространстве.
Вес тела – это абсолютное значение равнодействующей сил тяжести частиц, составляющих тело.

Координаты центра тяжести определяются по формулам:
(ЦТ2) .
Здесь – абсолютное значение равнодействующей сил тяжести, или вес тела. – координаты точек тела. Эти формулы также можно записать в векторном виде.
.
Центр тяжести C связан с телом. Однако его положение может находиться за его пределами. Например, при наличии полости.

В случае, когда силы имеют другое происхождение, но также имеют одинаковое направление, то мы имеем дело с системой параллельных сил. В этом случае, точка C называется центром параллельных сил.

Для сплошного однородного тела, мы от суммирования переходим к интегрированию. Элементарная сила тяжести выражается через плотность ρ_i элементарной частицы тела, массой , и занимающей объем :
.
Здесь g – ускорение свободного падения. Переходя от суммированию к интегрированию, имеем:
(ЦТ3) .

Центр тяжести плоской фигуры

Рассмотрим плоскую фигуру. Выберем двумерную систему координат Oxy . Тогда положение центра тяжести определяется по тем же формулам (ЦТ2) и (ЦТ3), из которых нужно убрать переменную z .

Однородная фигура

Рассмотрим плоскую однородную фигуру. Для такой фигуры, плотность ρ является постоянной; сила тяжести Δp_i элементарной частицы пропорциональна площади ΔA_i этой частицы: Δp_i = ρΔA_ig . Вес P фигуры пропорционален площади A всей фигуры: P = ρAg .

Подставляя эти величины в формулы, определяющие положение центра тяжести находим:
.
Переходим от суммирования к интегрированию:
.
Мы видим, что сюда не входят плотность ρ и ускорение свободного падения g . Остались величины, зависящие только от геометрии сечения. Таким образом, для тела с постоянной плотностью, центр тяжести является геометрической характеристикой.

В этих формулах, y_C есть алгебраическое расстояние от центра тяжести до оси x ; y_k или y – алгебраическое расстояние элементарного участка до той же оси. x_C , x_k и x – соответствующие алгебраические расстояния до оси y . В этой связи вводят новую геометрическую характеристику сечения, которую называют статическим моментом.

Статический момент относительно некоторой оси – это сумма произведений элементарных площадей , входящих в состав фигуры, на алгебраические значения их расстояний до этой оси.

В рассматриваемом нами случае, статические моменты относительно осей x, y определяются по формулам:
.
Статические моменты широко используются при расчете конструкций. Для стандартных профилей, их значения указываются в соответствующих справочниках.

Центры тяжести простейших фигур

Параллелограмм, прямоугольник, квадрат: в точке пересечения диагоналей.
Треугольник: в точке пересечения медиан, которая делит каждую медиану в соотношении 1:2.
Дуга окружности с центральным углом 2α: .
Круговой сектор: .

Теоремы, применяемые при расчете центра тяжести

Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости.

Центр тяжести фигуры, составленной из n более простых фигур, определяется по формуле:
(ЦТ4) .
Здесь – площадь всей фигуры; – площадь и координаты центра тяжести простой фигуры, входящей в состав сложной.

Способ отрицательных площадей (объемов)
Если k — я фигура вырезана из объемлющей ее части, то, в формуле (ЦТ4), соответствующая ей площадь считается отрицательной: .

Распределенная нагрузка

Силу тяжести протяженных тел, на схемах, изображают в виде эпюр. Также встречаются подобные силе тяжести параллельные силы, приложенные не в определенных точках тела, а непрерывно распределенные по его поверхности или объему. Такие силы называют распределенными силами или распределенными нагрузками.

Равномерно распределенная нагрузка q (рисунок А). Ее можно заменить равнодействующей силой величины , приложенной в центре тяжести эпюры. Поскольку, на рисунке А, эпюра представляет собой прямоугольник, то ее центр тяжести находится в центре основания эпюры – в точке C : | AC | = | CB | .

Линейно распределенная нагрузка q (рисунок В). Ее также можно заменить равнодействующей. Величина равнодействующей равна площади эпюры:
.
Точка приложения находится в центре тяжести эпюры. Центр тяжести треугольника, высотой h , находится на расстоянии от основания. Поэтому .

Приведение системы сил к центру

Теорема о параллельном переносе силы (лемма Пуансо)
Сила, действующая на данное тело, эквивалентна силе, полученной параллельным переносом исходной силы в любую точку тела и паре сил с моментом, равным моменту исходной силы относительно новой точки ее приложения.

Теорема о приведении системы сил к заданному центру
Любую систему сил, действующих на данное тело, можно привести к заданному центру O – то есть заменить одной силой, равной главному вектору, приложенной к точке приведения O , и парой сил с моментом M_O , равным главному моменту относительно центра O .

Статические инварианты

Такими инвариантами являются:
1) главный вектор ;
2) скалярное произведение главного вектора на главный момент .
Главный вектор равен векторной сумме всех сил и поэтому не зависит от центра приведения O . Главный момент зависит от положения центра O , относительно которого вычисляются моменты. Но величина его скалярного произведения на главный вектор не зависит от того, относительно какой точки вычисляется главный момент.

Хотя главный вектор не зависит от положения центра O , но величины его проекций на оси координат зависят от выбора системы координат. Поэтому они также не являются инвариантами. По той же причине и направление главного вектора не является инвариантом. Единственной численной величиной, которая не зависит от выбора системы координат, является модуль главного вектора. Но, в математическом отношении, проще иметь дело с квадратом модуля. Поэтому мы выберем его в качестве основного инварианта.

Итак, статическими инвариантами являются следующие величины:
– квадрат модуля главного вектора;
– скалярное произведение главного вектора на главный момент. Инвариантами также являются функции от инвариантов. Например, проекция главного момента на направление главного вектора является инвариантом:
.

Динама

Разложим главный момент на компоненту , параллельную главному вектору , и на компоненту , перпендикулярную :
(П1) .
Тогда .
Отсюда получаем упомянутый выше результат, что инвариантом является алгебраическая величина проекции главного момента на направление главного вектора:
.

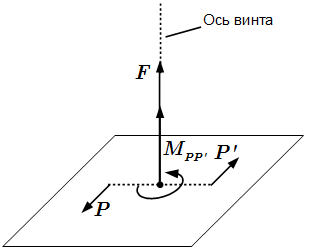
Динама – одна из простейших систем сил.

То есть, при изменении положения центра O , меняется вектор , в то время как вектор остается постоянным. Выбором центра приведения O , можно обратить в нуль. Тогда мы получим систему, состоящую из главного вектора и пары сил с моментом , лежащих в плоскости, перпендикулярной главному вектору. Такая система называется динамой или силовым винтом. Система приводится к динаме, если второй статический инвариант не равен нулю.

Динама – это простейшая система сил, состоящая из силы , приложенной к некоторой точке C , и паре сил, перпендикулярных . При этом момент пары параллелен линии действия силы. Динаму также называют силовым винтом, динамическим винтом, или статическим винтом.
Ось винта – это линия действия силы динамического винта.

Из (П1) мы находим, что минимальное значение модуля момента равно модулю его проекции на направление главного вектора:
.

Центральная ось системы сил

Пусть и – главный вектор и главный момент относительно некоторого центра O , который выберем за начало координат. И пусть второй инвариант отличен от нуля:
.
Найдем положение такой точки C , относительно которой система сил приводится к динаме. Для этого преобразуем главный момент от центра O к C :

.
Отсюда
(П2) .
Для динамы, векторы и направлены вдоль одной прямой. Поэтому
, где λ – некоторое число. Отсюда получаем два уравнения:
(П3) .
Пусть – компоненты вектора . Тогда подставив (П2) в (П3), имеем:
.
Это уравнение прямой в пространстве, которую называют центральной осью системы сил. Относительно точек этой прямой, система сил приводится к динаме, а главный момент имеет наименьшее по модулю значение.

Центральная ось системы сил – это прямая, обладающая тем свойством, что при приведении системы сил к любой из ее точек, система сил является динамой. При этом главный вектор и главный момент динамы параллельны этой прямой, а главный момент имеет наименьшее по модулю значение.

Приведение системы сил к простейшему виду

Пара сил

Пусть .
Тогда . Второй инвариант также равен нулю: . В этом случае, вектор главного момента не зависит от положения центра O . Система сил приводится к паре с моментом .

Если и , то это уравновешенная система сил. Она эквивалентна отсутствию сил.

Равнодействующая сила

Пусть .
В этом случае существует прямая, относительно точек которой главный момент равен нулю:
.
То есть система приводится к одной силе – равнодействующей, равной главному вектору приложенному к любой из точек упомянутой выше прямой. Эта прямая является линией действия главного вектора. Примеры: система сходящихся сил, система параллельных сил. Это системы, которые имеют равнодействующую.

Динама

При , как показано выше, система сил приводится к динаме.

Использованная литература:
А. А. Яблонский, В.М. Никифорова. Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Автор: Олег Одинцов . Опубликовано: 03-10-2017 Изменено: 07-05-2020