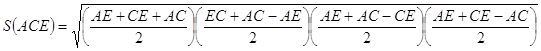2.14. Докажите, что через две скрещивающиеся прямые можно провести параллельные плоскости (рис. 36).
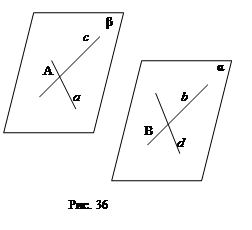
α || β (если две пересекающиеся прямые плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны).
3.06. Постройте сечение пятиугольной пирамиды PABCDE плоскостью α, которая проходит через внутреннюю точку М основания ABCDE параллельно грани РAB (рис. 37).
Решение: Так как прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны, а плоскость α параллельна грани РАВ, то: а) прямая пересечения плоскости α с плоскостью основания пирамиды должна быть параллельна АВ; б) прямая пересечения α с плоскостью грани РВС – 
3.07. Точки А, В и С лежат в плоскости α и не лежат на одной прямой. Равные и параллельные отрезки АА1, ВВ1 и СС1 расположены по одну сторону от плоскости α. Докажите, что (А1В1С1) || 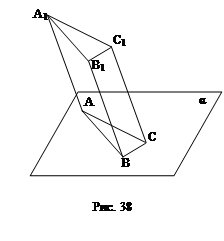
Решение: ВВ1С1С – параллелограмм (из параллельности и равенства ВВ1 и СС1), следовательно ВС || В1С1. АВ || А1В1 (аналогично). По теореме о параллельности плоскостей (по двум пересекающимся прямым): (А1В1С1) || (АВС).
3.08. Точка В не лежит в плоскости ΔAEC, точки М, К и Р – середины отрезков соответственно АВ, ВС и ВЕ (рис.39). а) Докажите, что плоскости МКР и АЕС параллельны. б) Найдите площадь ΔМКР, если площадь ΔAEC равна 48 см 2 .

б) По формуле Герона:
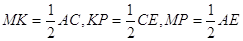
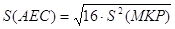
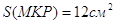
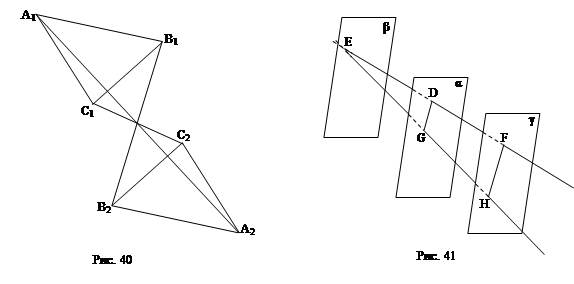
3.09. Три отрезка А1А2, В1В2 и С1С2, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А1В1С1 и А2В2С2 параллельны (рис. 40).
Решение: Каждые две пересекающиеся прямые задают плоскость (через любые две пересекающиеся прямые можно провести плоскость, и притом только одну). Так как точка пересечения делит прямые пополам, то по теореме Фалеса: А1В1 || В2А2. Аналогично доказывается параллельность С1В1 и С2В2, А1В1 и А2В2. По теореме о параллельности плоскостей (через пересекающиеся прямые): (А1В1С1)||(А2В2С2).
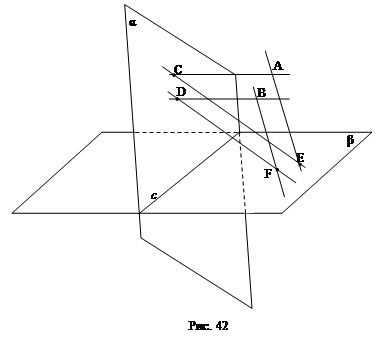
3.10. Прямая DF пересекает параллельные плоскости α, β и γ соответственно в точках D, Е и F, при этом DF = 3, ЕF = 9 (рис. 41). Прямая EG пересекает плоскости α и γ соответственно в точках G и Н, при этом EG = 12. Найдите длину GН.
Решение: Прямые EF и ЕH задают плоскость EFH, которая пересекает плоскости α и γ по прямым GD и FH соответственно. ∆GED
∆HEF (так как GD || FH, 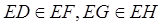
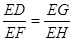
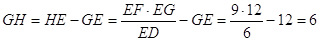
3.11. Плоскости α и β пересекаются по прямой с (рис. 42). Через точки А и В, расположенные вне этих плоскостей, проводятся параллельно плоскости β и параллельные между собой прямые АС и BD (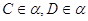
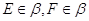
Решение: а) GА || DB, АЕ || FВ по условию. По теореме о параллельности плоскостей (через пересекающиеся прямые): (АСЕ) || (DBF).
б) BF и АЕ задают плоскость, параллельную плоскости α. По свойству параллельных плоскостей: EF || с. Аналогично CD || c. По признаку параллельности прямых: CD || EF.
5.3. Уроки проверки знаний, умений и навыков
Для проверки знаний, умений и навыков разработаны три задачи на выявление типов оперирования пространственными образами: изменение пространственного положения образа (I тип); преобразование структуры образа (II тип); изменение положения и структуры образа одновременно (III тип).
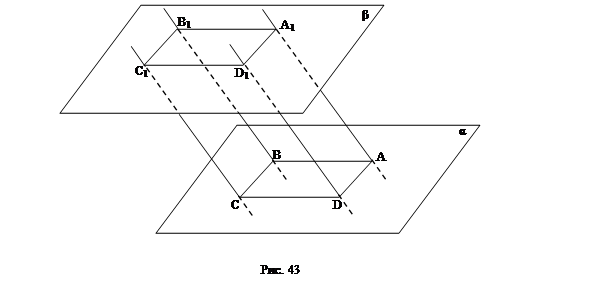
1. Через вершины параллелограмма ABCD, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А1, В1, С1 и D1. Докажите, что четырехугольник А1В1С1D1 тоже параллелограмм (рис. 43).
Решение: АА1 = DD1 = СС1 = ВВ1 (отрезки параллельных прямых, заключенные между параллельными плоскостями, равны). Попарно параллельные прямые задают параллелограммы (задание плоскости через параллельные прямые), следовательно D1А1 || DА || СВ || С1В1. По определению А1В1С1D1 параллелограмм.
- Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых плоскости, параллельной другой прямой
- Материал к уроку геометрии в 10 классе «Скрещивающиеся прямые. Угол между прямыми»
- Взаимное расположение прямых в пространстве
- Но надо жить без самозванства,
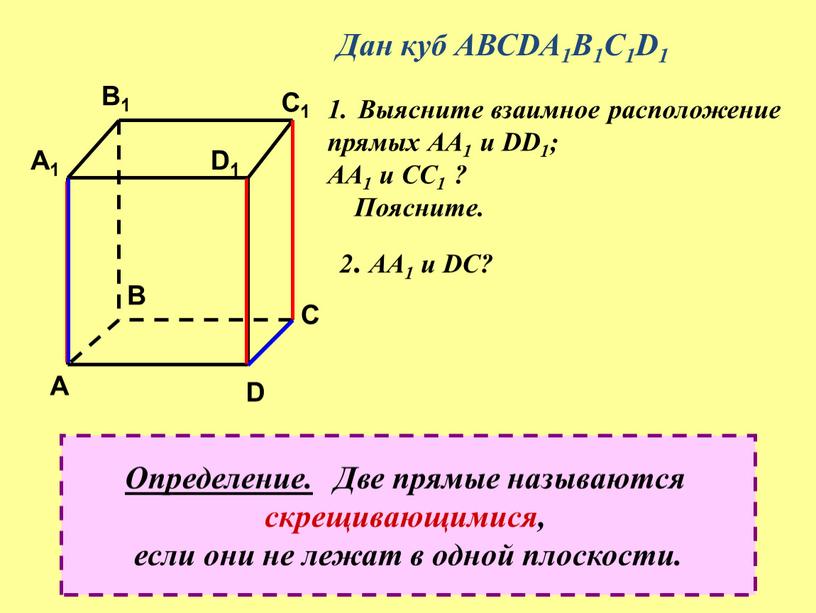
- Дан куб АВСDA1B1C1D1 Выясните взаимное расположение прямых
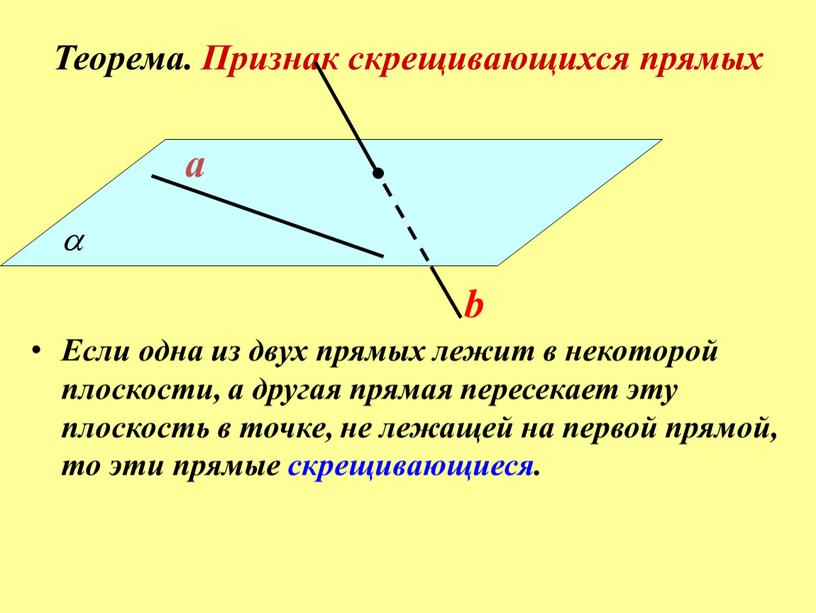
- Теорема. Признак скрещивающихся прямых
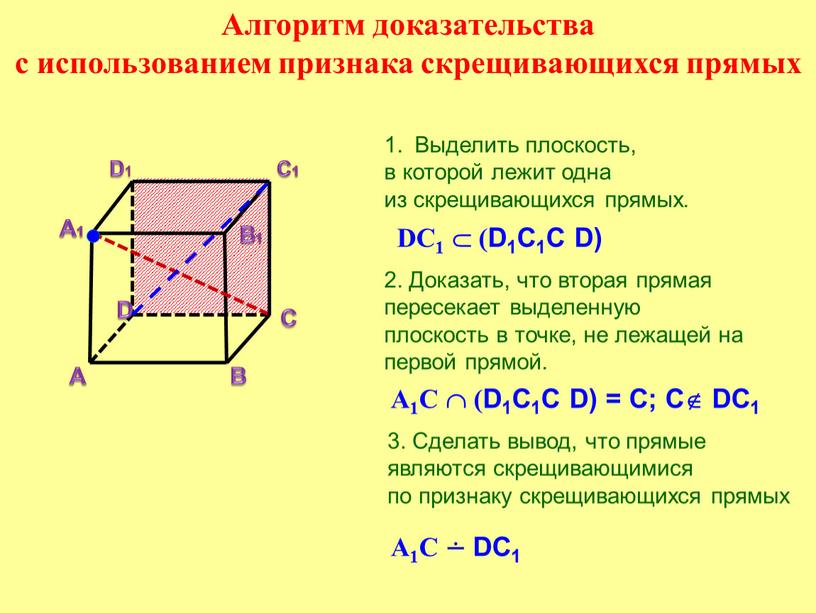
- Алгоритм доказательства с использованием признака скрещивающихся прямых
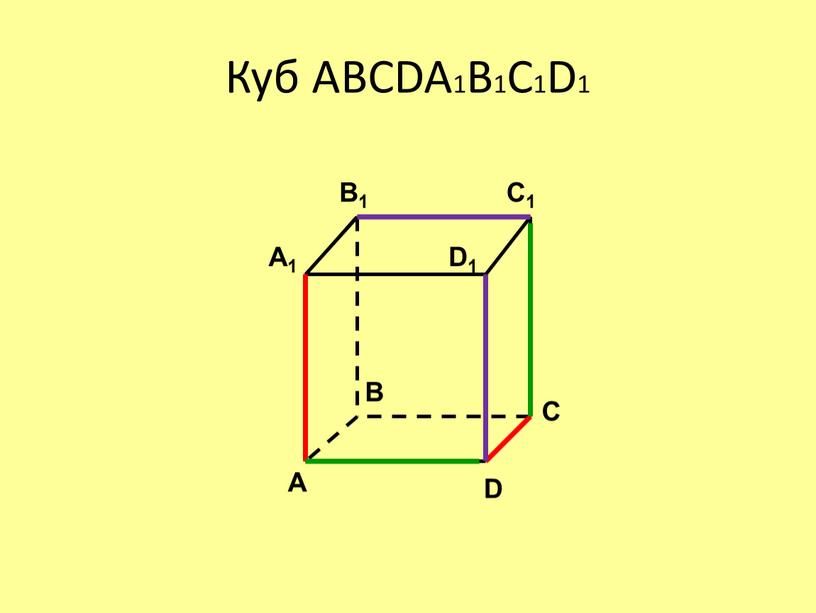
- Куб ABCDA1B1C1D1
- А В С D Тетраэдр DABC Скрещивающиеся ребра
- Задача №34. А В С D M N P Р1 К
- Задача №34 А В С D M N P К Дано:
- Задача №93 α a b М N Дано: a || b
- Определить взаимное расположение прямых
- Можно ли через одну из скрещивающихся прямых провести плоскость?
- О существовании параллельных плоскостей, проходящих через скрещивающиеся прямые
- Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна
- Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна
- 📸 Видео
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых плоскости, параллельной другой прямой
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых. Далее рассмотрим три случая взаимного расположения двух прямых в пространстве. Докажем теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
В конце урока решим несколько задач в тетраэдре на скрещиваемость прямых.
Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Материал к уроку геометрии в 10 классе «Скрещивающиеся прямые. Угол между прямыми»
Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве
Скрещивающиеся прямые
Угол между прямыми
Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Но надо жить без самозванства,
Но надо жить без самозванства,
Так жить, чтобы в конце концов
Привлечь к себе любовь
пространства,
Услышать будущего зов.
Б. Л. Пастернак
Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Дан куб АВСDA1B1C1D1 Выясните взаимное расположение прямых
Дан куб АВСDA1B1C1D1
Выясните взаимное расположение
прямых АА1 и DD1;
АА1 и СС1 ?
Поясните.
Определение. Две прямые называются
скрещивающимися,
если они не лежат в одной плоскости.
Видео:Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

Теорема. Признак скрещивающихся прямых
Теорема. Признак скрещивающихся прямых
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Алгоритм доказательства с использованием признака скрещивающихся прямых
Алгоритм доказательства
с использованием признака скрещивающихся прямых
Выделить плоскость,
в которой лежит одна
из скрещивающихся прямых.
2. Доказать, что вторая прямая
пересекает выделенную
плоскость в точке, не лежащей на
первой прямой.
3. Сделать вывод, что прямые
являются скрещивающимися
по признаку скрещивающихся прямых
А1C (D1C1С D) = С; С DC1
Видео:10 класс - Геометрия - Скрещивающиеся прямыеСкачать

Куб ABCDA1B1C1D1
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

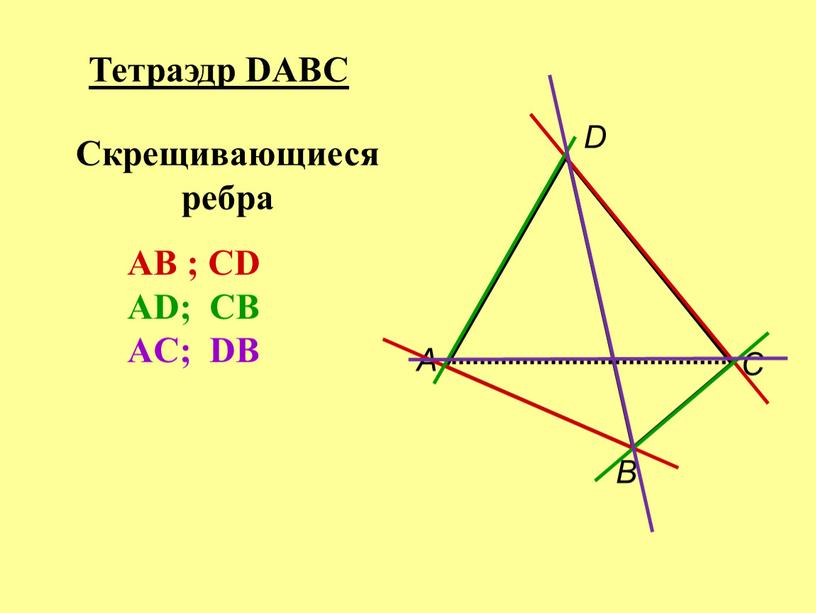
А В С D Тетраэдр DABC Скрещивающиеся ребра
AB ; CD
AD; CB
AC; DB
Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

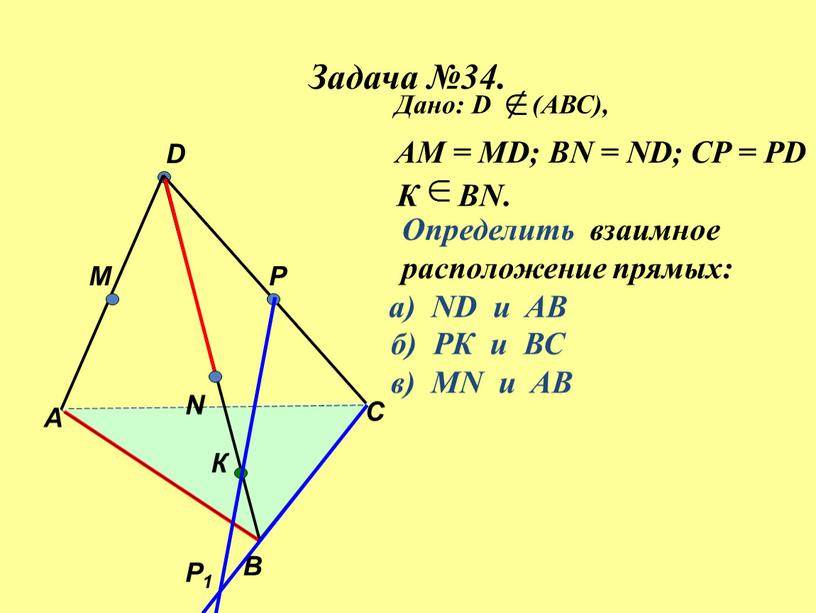
Задача №34. А В С D M N P Р1 К
АМ = МD; ВN = ND; CP = PD
Определить взаимное
расположение прямых:
Видео:Геометрия 10 класс : Параллельные плоскости и их свойстваСкачать

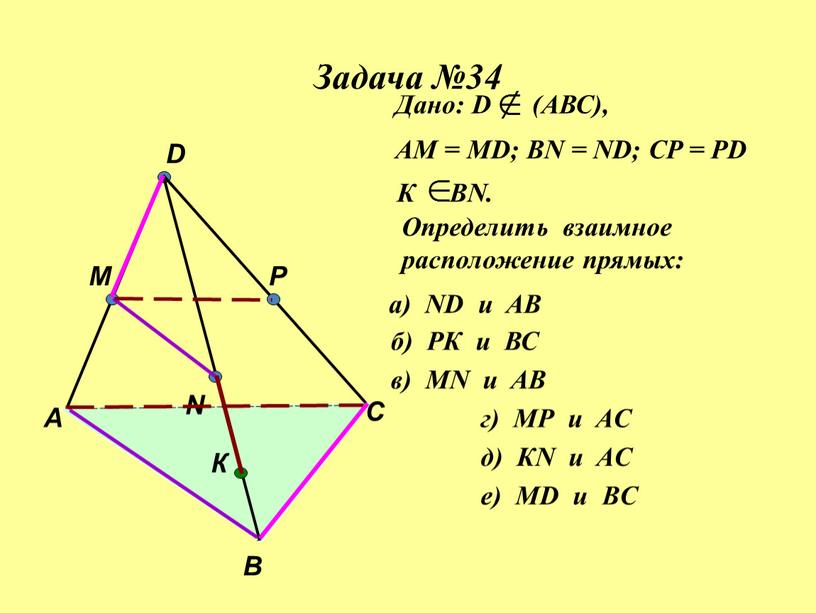
Задача №34 А В С D M N P К Дано:
АМ = МD; ВN = ND; CP = PD
Определить взаимное
расположение прямых:
Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

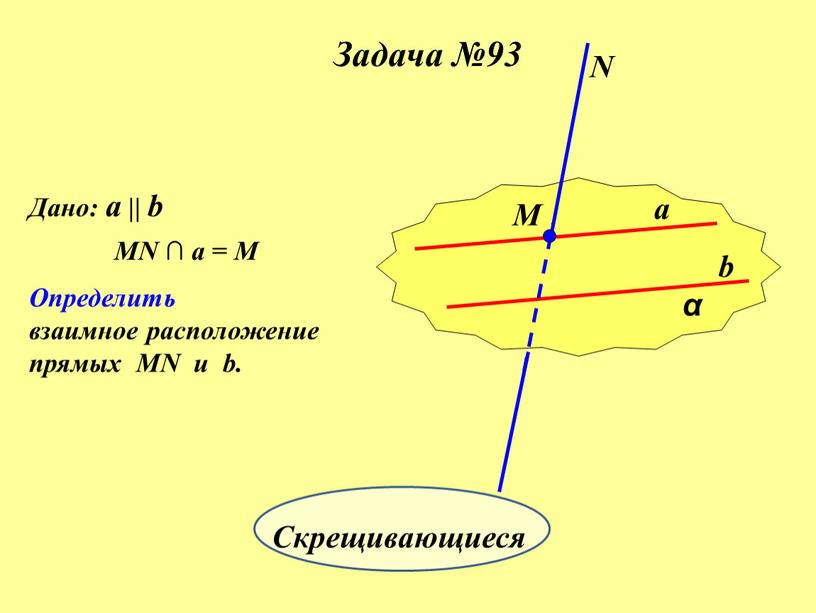
Задача №93 α a b М N Дано: a || b
Определить
взаимное расположение
прямых MN u b.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

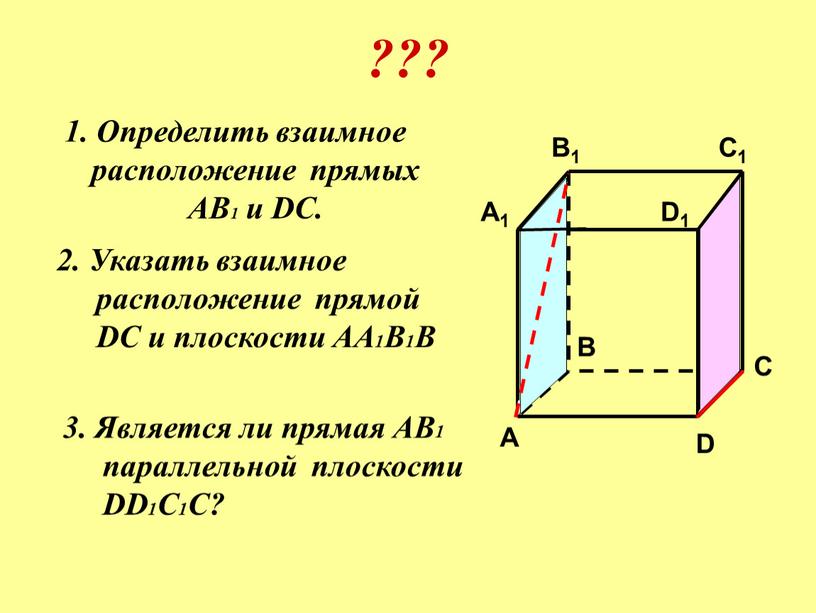
Определить взаимное расположение прямых
1. Определить взаимное
расположение прямых
АВ1 и DC.
2. Указать взаимное
расположение прямой
DC и плоскости АА1В1В
3. Является ли прямая АВ1
параллельной плоскости
DD1С1С?
Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

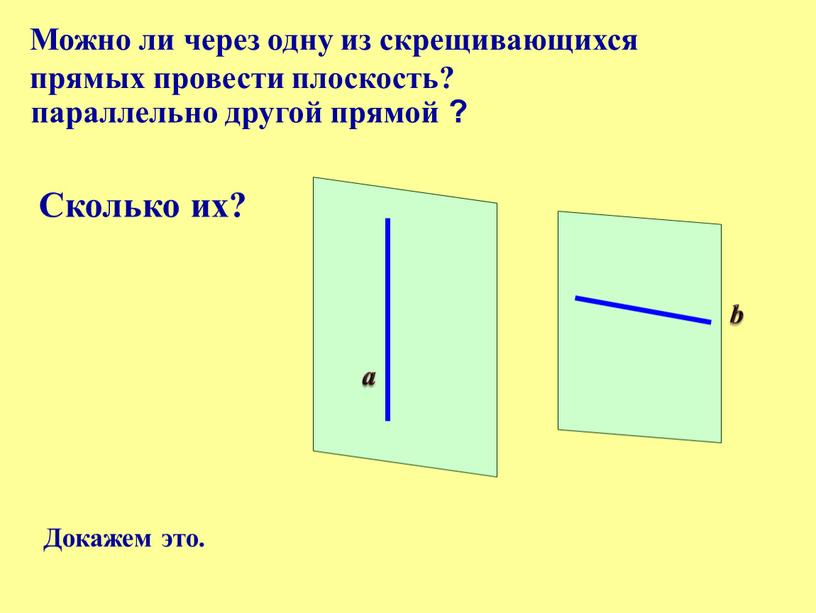
Можно ли через одну из скрещивающихся прямых провести плоскость?
Можно ли через одну из скрещивающихся
прямых провести плоскость?
параллельно другой прямой
Видео:СТЕРЕОМЕТРИЯ. ВСЕ ЗАДАЧИ НА ПАРАЛЛЕЛЬНОСТЬСкачать

О существовании параллельных плоскостей, проходящих через скрещивающиеся прямые
О существовании параллельных плоскостей, проходящих через скрещивающиеся прямые
Видео:Параллельность прямых. 10 класс.Скачать

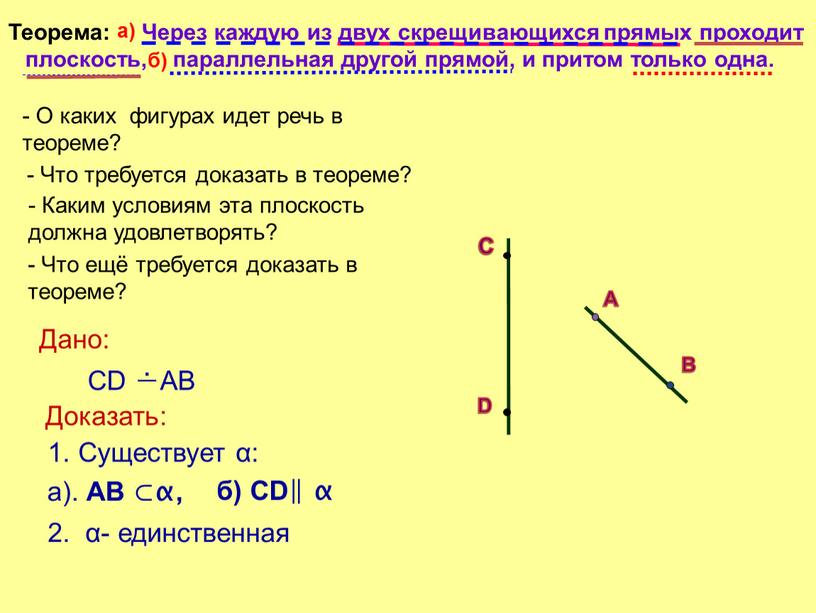
Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна
Теорема: Через каждую из двух скрещивающихся прямых проходит
плоскость, параллельная другой прямой, и притом только одна.
— О каких фигурах идет речь в теореме?
— Что требуется доказать в теореме?
2. α- единственная
— Каким условиям эта плоскость должна удовлетворять?
а). AB ⊂α,
— Что ещё требуется доказать в теореме?
Видео:ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ 10 класс стереометрияСкачать

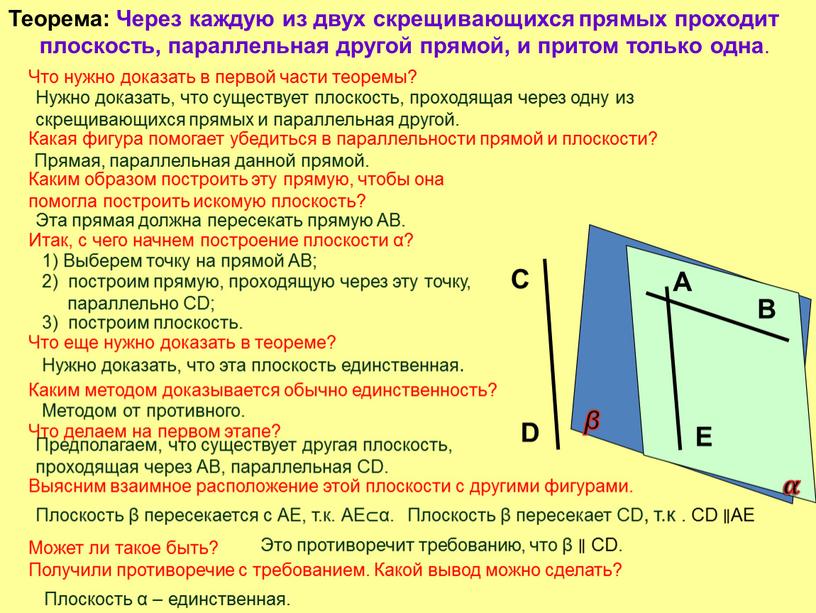
Теорема: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна
Теорема: Через каждую из двух скрещивающихся прямых проходит
плоскость, параллельная другой прямой, и притом только одна.
Что нужно доказать в первой части теоремы?
Нужно доказать, что существует плоскость, проходящая через одну из
скрещивающихся прямых и параллельная другой.
Какая фигура помогает убедиться в параллельности прямой и плоскости?
Прямая, параллельная данной прямой.
Каким образом построить эту прямую, чтобы она
помогла построить искомую плоскость?
Эта прямая должна пересекать прямую АВ.
Итак, с чего начнем построение плоскости α?
Что еще нужно доказать в теореме?
2) построим прямую, проходящую через эту точку,
параллельно CD;
3) построим плоскость.
Нужно доказать, что эта плоскость единственная.
1) Выберем точку на прямой АВ;
Каким методом доказывается обычно единственность?
Методом от противного.
Что делаем на первом этапе?
Предполагаем, что существует другая плоскость,
проходящая через АВ, параллельная CD.
Выясним взаимное расположение этой плоскости с другими фигурами.
Плоскость β пересекается с АЕ, т.к. АЕ⊂α.
Получили противоречие с требованием. Какой вывод можно сделать?
📸 Видео
Стереометрия для ЕГЭ: 2 - параллельные и скрещивающиеся прямыеСкачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

Угол между прямыми в пространстве. 10 класс.Скачать