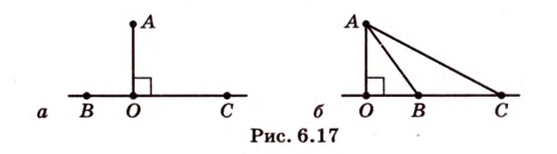
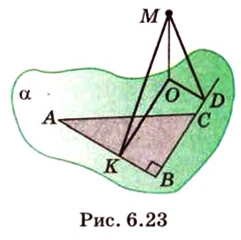
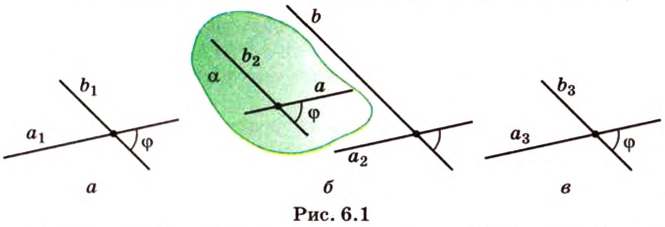
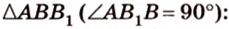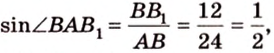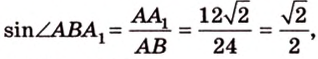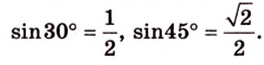Следствие. Углы образованные соответственно параллельными прямыми, равны.
 |
Определение. Пусть a и b – скрещивающиеся прямые. Рассмотрим какую-нибудь точку С в пространстве и проведём через неё прямые a’, b’, параллельные прямым a и b, соответственно. Угол между пересекающимися прямыми a’, b’ называется углом между скрещивающимися прямыми a и b.
Определение. Две скрещивающиеся прямые называются перпендикулярными, если они образуют прямой угол.
Определение. Два отрезка называются перпендикулярными, если они лежат на перпендикулярных прямых. Угол между двумя отрезками – это угол между соответствующими прямыми.
2. Проверьте усвоение теоретического материала. Ответьте на вопросы для самоконтроля
1. Что называется углом в пространстве?
2. Сформулируйте определение угла между двумя пересекающимися прямыми в пространстве.
3. Какие пересекающиеся прямые в пространстве называются перпендикулярными?
4. Какие лучи в пространстве являются соноправленными?
5. Как найти угол между скрещивающимися прямыми?
6. Сформулируйте теорему об углах с соноправленными сторонами.
3. Примите участие в учебной беседе. Материал для беседы
1. Докажите, что через точку прямой в пространстве можно провести перпендикулярную прямую. Сколько таких прямых можно провести через данную точку?(бесконечно много).
2. В кубе АBCDA1B1C1D1 найдите углы между скрещивающимися прямыми: а) АD и A1C1; б) АС1 и DD1; a) 45o; б) tg 4= Ö2.
3. В кубе АBCDA1B1C1D1 докажите перпендикулярность прямых: АD и А1B1; АС и B1D1; АС и DD1.
4. Прямые a и b параллельны. Прямые a и c пересекаются под прямым углом. Изобразите взаимное расположение прямых b и c и укажите угол между ними (рассмотрите различные случаи).
4. Самостоятельно выполните задания, затем проверьте решение
1. Докажите, что пересекающиеся диагонали двух соседних граней куба образуют угол 60о.
2. Найдите угол между диагональю куба и пересекающим ее ребром куба.
 |
3. В правильной четырех угольной пирамиде со стороной основания, равной боковому ребру, найдите угол между стороной основания и скрещивающимися с ней боковым ребром.
6. Проверьте освоение данного модуля, выполните контрольные задания
Основной уровень:1. В пирамиде все грани которого – правильные треугольники, найдите угол между высотами этих треугольников, проведенных к общему ребру. 2. В треугольной призме, боковыми гранями которого являются квадраты, найдите угол между пересекающимися диагоналями боковых граней.
Повышенный уровень: На поверхности куба найдите точки из которых диагональ куба видна под наименьшим углом.
Перельман Я.И. Занимательная геометрия. – М.: ВАП, 1994.
1. Ознакомьтесь со следующими теоретическими положениями
Определение. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Образование в Японии
Курс школьного обучения в Японии занимает 12 лет, и половина его приходится на начальную школу из-за исключительной сложности и трудоемкости изучения родного языка. Ученики должны усвоить 1850 иероглифов — минимум, установленный министерством просвещения (но даже для чтения книг и газет требуется з .
Причины минимальных дизартрических расстройств
Минимальные дизартрические расстройства возникают при двустороннем поражении двигательных корково-ядерных путей, идущих от коры головного мозга к ядрам черепных нервов ствола. Вследствие большой вариативности и комбинантности поражения двигательных проводящих путей черепно-мозговых нервов симптомат .
Способы стимулирования познавательной активности подростков на уроках английского языка
При изучении новой лексики по теме можно применять такие игровые методы как кроссворд, составление истории по картинке. Например, игра «Word-search grid» . Дается сетка 14×14 клеток, в каждой клетке написана буква алфавита. Среди набора букв скрыты слова по теме «деньги». Учащимся необходимо .
- Углы и расстояния в пространстве — определение и вычисление с примерами решения
- Угол между двумя прямыми в пространстве
- Угол между прямой и плоскостью в пространстве
- Угол между двумя плоскостями, пространства
- Пример №1
- Расстояния в пространстве
- Пример №2
- Пример №3
- Пример №4
- Углы, образованные параллельными прямыми
- Просмотр содержимого документа «Углы, образованные параллельными прямыми»
- 🎥 Видео
Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Углы и расстояния в пространстве — определение и вычисление с примерами решения
Содержание:
В планиметрии угол — это геометрическая фигура, образованная двумя лучами, которые выходят из одной точки — вершины угла (лучи — стороны угла). Такое определение понятия угла переносится и в стереометрию. Углы в пространстве рассматриваются между двумя прямыми, прямой и плоскостью, двумя плоскостями. Опишем и определим каждый из этих случаев.
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Угол между двумя прямыми в пространстве
Две прямые, лежащие в одной плоскости, при пересечении образуют смежные и вертикальные углы. В модуле 1 мы повторили все свойства таких углов (вертикальные углы равны, а смежные — дополняют друг друга до 180°). В пространстве (аналогично планиметрии) также сохраняются все названия и понятия об углах и их величинах. Меньший из углов, образованных двумя пересекающимися прямыми, называют углом между прямыми. Угол между перпендикулярными прямыми равен 90°. Считают, что параллельные прямые также образуют угол, равный 0°. В стереометрии рассматривают угол между скрещивающимися прямыми. Пусть даны скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся. 
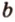
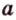
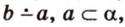
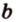
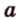
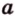
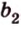
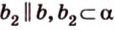
Итак,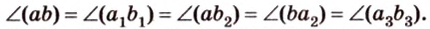
Если 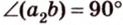
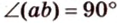
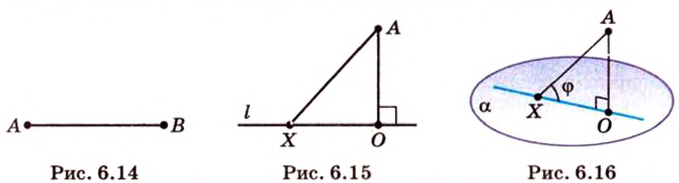
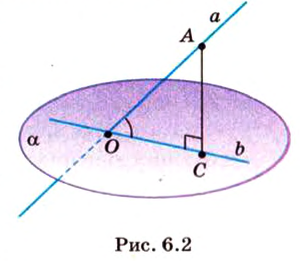
Угол между прямой и плоскостью в пространстве
Об угле наклона прямой к плоскости говорят в том случае, когда прямая пересекает эту плоскость. Чтобы построить, например, угол между прямой 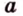
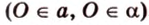
- выбирают точку
прямой
;
- проводят из точки
перпендикуляр к плоскости
;
- проводят через точки плоскости
и
прямую
.
Прямую 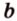
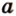
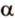
Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая 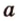
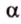
Угол между прямой 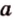
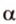
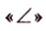
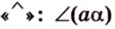
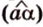
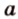
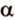
Угол между двумя плоскостями, пространства
Прямая на плоскости разбивает ее на две полуплоскости. Две полуплоскости могут иметь общую прямую и не образовывать одну плоскость. В этом случае они образуют фигуру, которую называют двугранным углом.
Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.
Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные
полуплоскости, образуют линейный угол, например 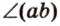
Пересекающиеся плоскости образуют четыре угла. Чтобы определить угол между двумя плоскостями, проводят плоскость, перпендикулярную прямой их пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называется углом между данными плоскостями. Т.е. угол между двумя пересекающимися плоскостями — это угол между двумя прямыми, которые принадлежат этим плоскостям и перпендикулярны прямой их пересечения.
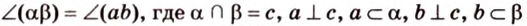
Если линейный угол — 90°, то плоскости перпендикулярны. Если плоскости параллельны, то угол между ними равен 0°.
Теорема 1
Угол между плоскостями не зависит от места построения линейного угла.
Выберем точки 
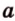
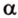
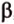
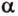
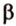
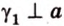
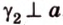
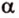
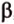
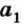
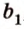
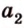
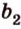
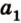
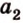
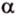
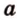
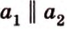
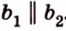
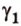
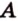
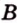
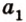
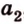
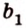
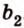
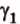
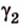
Пример №1
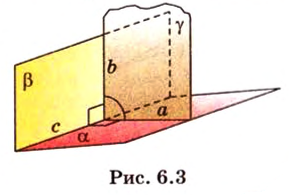
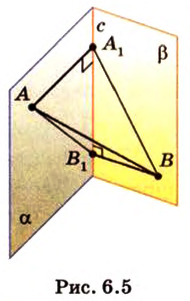
Концы отрезка длиной 24 см принадлежат двум перпендикулярным плоскостям. Расстояния от концов отрезка до линии пересечения данных плоскостей равны 12 см и 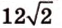
Дано: 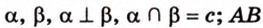
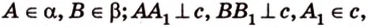
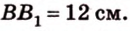
Найти: углы, образованные отрезком 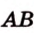
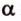
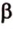
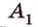
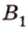
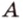
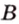
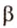
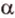
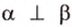
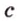
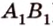
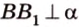
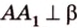
Итак, 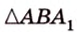
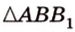
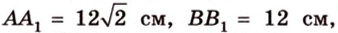
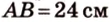
Из 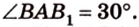
Из 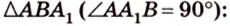
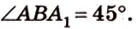
Ответ. 30°; 45°.
Почему именно так?
В этой задаче важно построить проекции концов отрезка на другую, перпендикулярную ей, плоскость. При этом следует помнить, что они должны лежать на прямой пересечения данных перпендикулярных плоскостей, согласно свойствам перпендикулярных плоскостей. Далее, рассматривая прямоугольные треугольники, нужно правильно использовать определение синуса угла как отношения противолежащего катета к гипотенузе и таблицу значений:
Расстояния в пространстве
Одним из ключевых понятий геометрии является длина отрезка. Через него вводится много других понятий, связанных с понятием расстояния. Как известно, расстоянием между двумя точками 
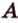
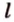
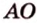
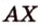
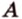
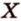
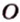
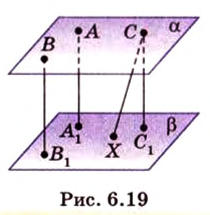
Рассмотрим плоскость 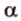
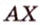
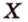
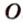
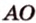
Итак, расстояние от точки до плоскости равно длине перпендикуляра, проведенного из этой точки к плоскости.
Если точка принадлежит плоскости, то в этом случае расстояние от нее до плоскости равно нулю.
Расстояние от точки 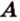
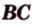
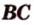
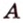
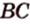
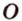
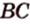
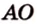

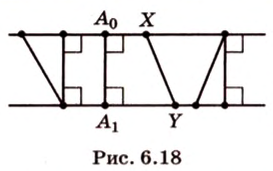
Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (рис. 6.18). Это вытекает из того, что все такие перпендикуляры 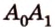
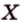
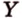
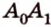
Теорема 2 (о расстоянии между параллельными прямой и плоскостью)
Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из произвольной точки прямой к плоскости.
Данная теорема доказывается рассуждениями, аналогичными приведенным выше, о расстоянии между параллельными прямыми.
Теорема 3 (о расстоянии между параллельными плоскостями)
Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из произвольной точки одной плоскости ко второй.
Пусть имеем две параллельные плоскости 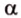
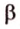
и второй, то перпендикуляр 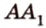
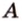
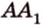
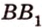
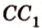
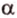
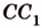
А это вытекает из того, что перпендикуляр 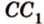
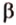
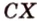
Понятие расстояния между точками широко применяется в разнообразных сферах жизни человека — от науки до быта и досуга. Используется оно в тех случаях, когда размерами реальных объектов, расстояние между которыми вычисляется, в данных условиях можно пренебречь. Так мы говорим о расстоянии между звездами, планетами, передатчиками и принима-телями информации, населенными пунктами, ядрами атома и электронами на его орбите и т.п.
Расстояние между скрещивающимися прямыми
Сначала рассмотрим определение перпендикуляра, проведенного к двум скрещивающимся прямым, и докажем его существование и единственность.
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
Теорема 4
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром к параллельным плоскостям, проходящим через эти прямые.
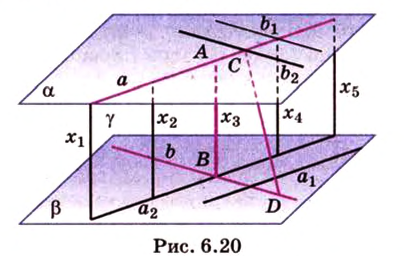
Действительно, пусть 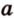
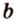
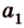
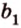
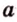
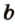
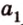
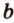
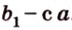
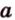
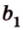
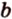
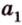
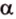
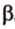
Плоскости 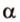
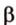
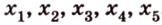
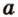
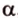
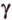
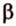
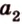
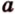
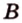
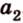
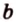
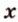
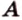
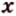
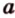
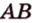
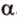
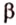
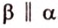
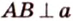
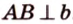
Отрезок 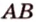
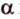
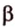
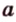
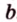
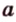
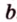
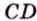
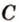
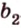
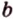

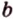
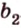
Поскольку она перпендикулярна прямым 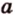
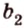

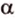




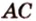
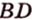
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
Пример №2
Отрезок 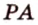
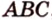
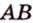
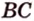
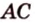
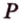
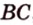
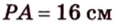
Пусть 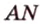
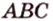
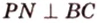
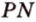
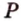
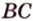
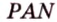
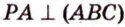
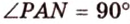
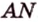
Из формулы для площади треугольника 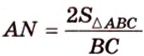
Необходимую площадь определим по формуле Герона: 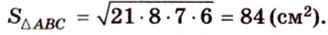
Тогда 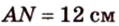
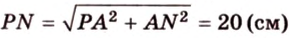
Пример №3
Прямая 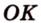
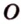
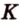
Пусть 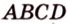
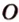
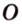
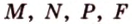
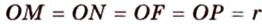
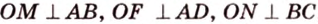
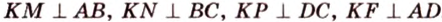
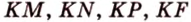
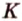
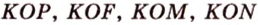
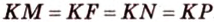
Пример №4
Точка 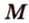
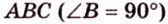
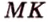
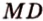
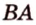
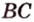
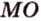
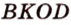
Поскольку отрезки 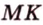
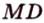
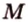
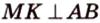
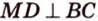
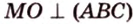
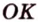
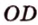
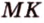
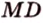
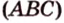
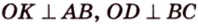
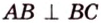
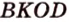
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
- Теорема синусов и теорема косинусов
- Квадрат и его свойства
- Трапеция и ее свойства
- Площадь трапеции
- Центральные и вписанные углы
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Углы, образованные параллельными прямыми
Презентация — подробное и наглядное изложение темы » Углы, образованные параллельными прямыми». В ней рассматриваются понятие обратной теоремы, метода от противного, теорем о свойствах углов, образованных параллельными прямыми и секущей, приведены задачи для закрепления рассматриваемой темы.
Просмотр содержимого документа
«Углы, образованные параллельными прямыми»
Теоремы об углах, образованных двумя параллельными прямыми и секущей
Геометрия, Глава III, 7 класс
К учебнику Л.С.Атанасяна
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
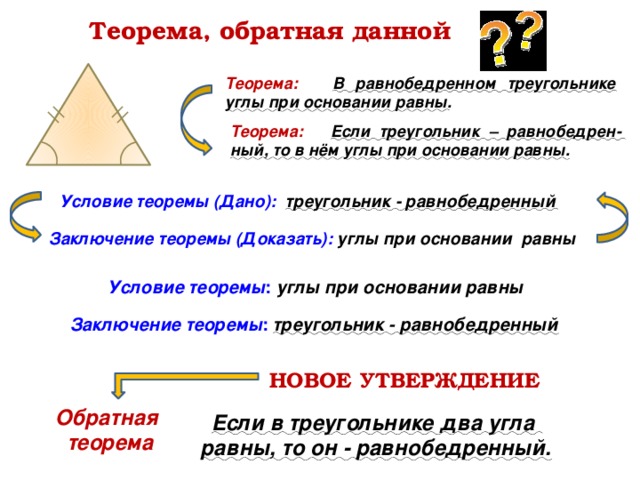
Теорема, обратная данной
Теорема: В равнобедренном треугольнике углы при основании равны .
Теорема: Если треугольник – равнобедрен-ный, то в нём углы при основании равны .
Условие теоремы (Дано): треугольник — равнобедренный
Заключение теоремы (Доказать): углы при основании равны
Условие теоремы : углы при основании равны
Заключение теоремы : треугольник — равнобедренный
Если в треугольнике два угла
Теорема, обратная данной
Всегда ли обратное утверждение верно?
Если сумма двух углов равна 180 0 , то углы — смежные
Сумма смежных углов
то они — вертикальные
Вертикальные углы равны
Если в треугольнике биссектриса, проведенная к одной из его сторон, является и медианой, проведенной к этой стороне, то этот треугольник -равнобедренный
В равнобедренном треугольнике, биссектриса, проведенная к основанию, является медианой и высотой
Если в треугольнике биссектриса, проведенная к одной из его сторон, является и высотой, проведенной к этой стороне, то этот треугольник -равнобедренный
Е сли треугольник — равнобедренный, то биссектриса, проведенная к основанию , является и медианой и высотой
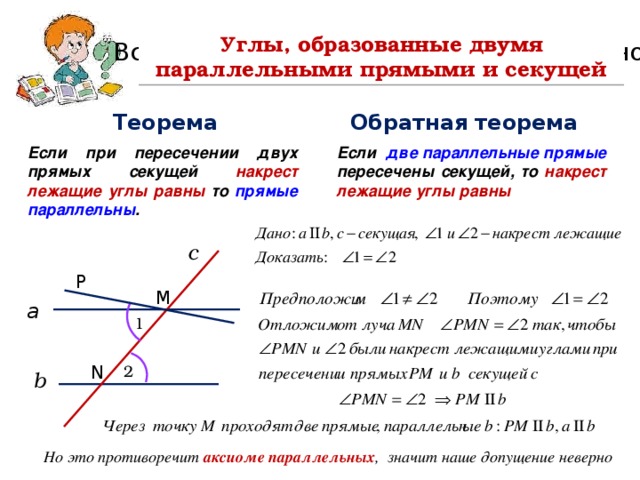
Углы, образованные двумя параллельными прямыми и секущей
Всегда ли обратное утверждение верно?
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
Если при пересечении двух прямых секущей накрест лежащие углы равны то прямые параллельны .
Но это противоречит аксиоме параллельных , значит наше допущение неверно
🎥 Видео
29. Теорема об углах, образованных двумя параллельными прямыми и секущейСкачать

Геометрия 7 класс. Теоремы об углах, образованных двумя параллельными прямымСкачать

14. Угол между прямыми в пространствеСкачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

Пары углов в геометрииСкачать

19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать

Как проверяют учеников перед ЕНТСкачать

Угол между прямыми, плоскостями, прямой и плоскостью | Математика ЕГЭ для 10 класса | УмскулСкачать

Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Расстояние между параллельными прямымиСкачать

Теоремы об углах, образованных двумя параллельными прямыми и секущей.Скачать

Углы, образованные параллельными прямыми и секущейСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Теоремы об углах, образованных двумя параллельными прямыми и секущей. Решение задач.Скачать

Свойства углов, образованных двумя параллельными прямыми и секущей Задачи на признаки параллельностСкачать

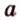
 прямой
прямой 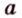
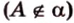 ;
;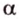
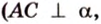
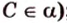 ;
;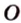 и
и 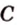 прямую
прямую 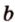 .
.