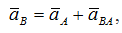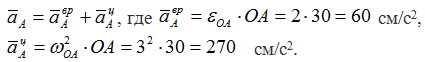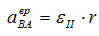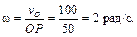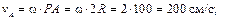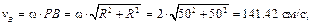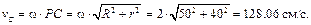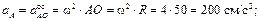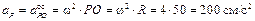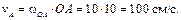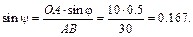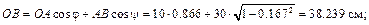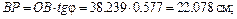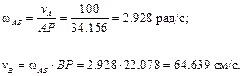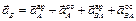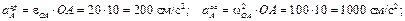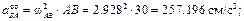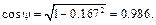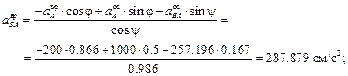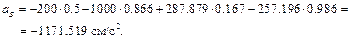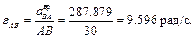Векторы скорости точек колеса

Видео:ВЕЛОСИПЕДНЫЕ ЦЕПИ на КОЛЕСА = УПРАВЛЕНИЕ +107Скачать

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

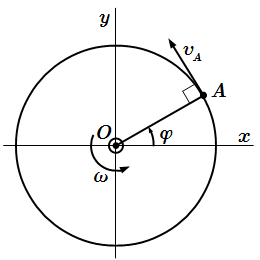
Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

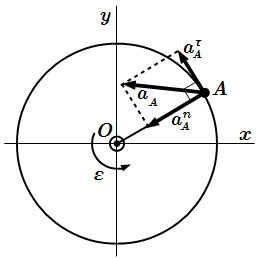
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Видео:Задача. Скорость точек дискаСкачать

Пример решения задачи

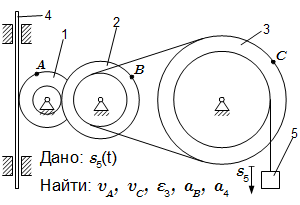
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

Видео:Движение колеса без проскальзывания, качение | Олимпиадная физика, кинематика | 9 – 11 классСкачать

iSopromat.ru

Пример решения задачи по определению величины и направления полной скорости и полного ускорения при сложном движении точки колеса кривошипа.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Задача

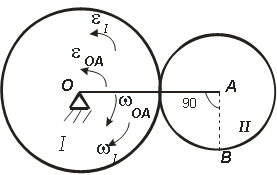
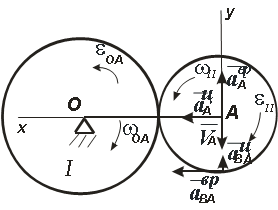
Колесо I с радиусом R вращается вокруг оси,
проходящей через центр колеса перпендикулярно плоскости чертежа с угловой скоростью ω_I и угловым ускорением ε_I.

Независимо от него на той же оси вращается кривошип ОА с угловой скоростью ω_OA и угловым ускорением ε_OA. Кривошип приводит в движение колесо II с радиусом r, которое катится по колесу I (рис. 2.7).

Видео:Скорости и ускорения точек вращающегося телаСкачать

Решение

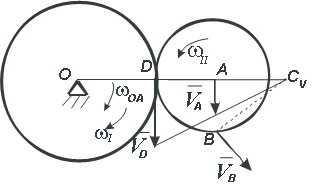
Найдем скорость точки В, для этого определим положение мгновенного центра скоростей колеса II. Чтобы найти МЦС нужно, знать направление скоростей хотя бы двух точек тела.

Найдем скорость точки А, которая принадлежит колесу II и кривошипу ОА.

Вектор V_A направлен перпендикулярно отрезку ОА в сторону вращения кривошипа (рис. 2.8).

В точке соприкосновения колес скорость точки колеса II должна равняться скорости точки колеса I. Обозначим эту точку буквой D. Эта точка не принадлежит кривошипу ОА. Так как движение колеса I известно, можно найти скорость точки D.

Вектор скорости точки D направлен перпендикулярно радиусу OD в сторону вращения колеса I. Таким образом, нам известны скорости двух точек колеса II. Проведем перпендикуляр к скоростям в точках А и D и прямую, проходящую через концы векторов скоростей V_D и V_A.

В точке пересечения этих линий и будет МЦС для колеса II. Обозначим его буквой C_V. Найдем расстояние AC_V:

Зная угловую скорость колеса II и его МЦС, найдем скорость точки В.

Вектор V_B направлен перпендикулярно отрезку ВС_V в сторону вращения колеса II.

Определим ускорение точки В.

Согласно теореме, ускорение точки В определятся по формуле

где a_A — ускорение точки А, принятой за полюс;

a_BA — ускорение точки В во вращательном движении, вокруг
полюса А.

Точка А принадлежит кривошипу ОА – движение которого известно, тогда

Вектор a τ _A — направлен перпендикулярно ОА, в сторону, обратную V_A, т.к. вращение кривошипа по условию задачи замедленное.

Вектор a n _A — направлен от А к О.

и направлен от точки В к полюсу А.

Для его вычисления найдем угловое ускорение ε_II:

r – в задачах такого типа величина постоянная, выносится за знак производной:

Знак «-» говорит о том, что колесо II вращается замедленно.

и направлена перпендикулярно a n _BA. Полное ускорение найдем, сложив все слагаемые:

Направив ось АX вдоль АО, ось АY перпендикулярно АО, получим:

Вектор a_B составляет с осью АХ угол α, косинус
которого

а с осью AY угол β, косинус которого:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Урок относительность 04 колесоСкачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:Мгновенный центр вращенияСкачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Вращательное движение. 10 класс.Скачать

Мгновенный центр скоростей

Простой и наглядный способ определения скоростей плоской фигуры основан на понятии о мгновенном центре скоростей (МЦС). Им называют точку подвижной плоскости, в которой расположена плоская фигура S и скорость которой в данный момент времени равна нулю.

Доказана теорема о том, что если тело движется не поступательно, то такая точка существует, и притом единственная. Из определения следует, что в общем случае в каждый момент времени МЦС находится в различных точках плоскости. При вращательном движении тела вокруг неподвижной оси, являющимся частным случаем плоскопараллельного движения, МЦС в любой момент времени расположен на оси вращения. Если же тело движется поступательно или мгновенно поступательно (скорости всех точек тела в данный момент времени равны по величине и совпадают по направлению), то МЦС находится на бесконечно большом расстоянии от любой точки тела. 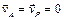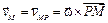Выбрав в качестве полюса точку Р, которая является в данный момент времени МЦС, а значит , из формулы (3.4) для определения скорости любой точки плоской фигуры найдем скорость точки М

. (3.8)

Следовательно, скорость любой точки тела в данный момент времени находим так же, как при вращении вокруг неподвижной оси, проходящей через МЦС и перпендикулярной плоскости движения. Таким образом, при плоскопараллельном движении скорость любой точки тела перпендикулярна отрезку, соединяющему эту точку с МЦС, а модуль скорости пропорционален расстоянию до МЦС

(3.9)

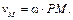
Угловая скорость плоской фигуры равна отношению скорости какой-либо ее точки к расстоянию от этой точки до МЦС

(3.10)

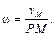
Способы определения положения мгновенного центра скоростей:

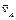
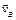
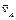
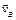
1) если известны направления скоростей и точек А и В плоской фигуры, то МЦС (точку Р) определяют как точку пересечения перпендикуляров к скоростям и , проведенных из этих точек (рис. 3.3,а);

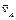
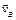
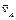
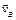
2) если скорости двух точек тела A и B известны по модулю, параллельны друг другу ( || ), и перпендикулярны прямой AB, то МЦС находят в точке пересечения прямой АВ с прямой, соединяющей концы векторов скоростей и (рис. 3.3,б,в);

3) при качении без скольжения одного тела по неподвижной поверхности МЦС находят в точке соприкосновения тел (рис. 3.3,г), так как при отсутствии скольжения скорость этой точки подвижного тела равна нулю;

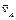
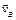
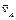
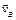
4) если скорости точек A и B тела и параллельны друг другу ( || ) и не перпендикулярны прямой АВ, то перпендикуляры к ним также параллельны друг другу. В этом случае МЦС находится в бесконечном удалении от точек A и B, движение тела является мгновенно поступательным, следовательно, скорости всех точек тела равны, а его угловая скорость в данный момент времени равна нулю.

С помощью МЦС плоскопараллельное движение можно представить не только как сложное, состоящее из поступательного и вращательного движений, но и как простое движение, состоящее из серии элементарных последовательных поворотов вокруг МЦС. Необходимо отметить, что положение МЦС в пространстве во все время движения меняется. Геометрическое место точек МЦС подвижного тела называют подвижной центроидой, а неподвижного тела – неподвижной центроидой. Таким образом, плоскопараллельное движение представляет собой качение без скольжения подвижной центроиды по неподвижной центроиде.

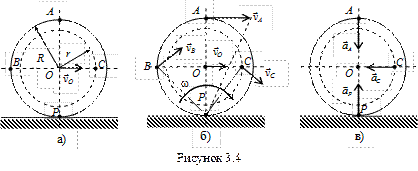
Пример 1. Колесо катится без скольжения по неподвижной прямой поверхности. Скорость точки O постоянна и равна 100 см/с (рис. 3.4,а).

Определить угловую скорость колеса, скорости точек A, B, C и ускорения точек A, C, P, если R = 50 см, r = 40 см.

Колесо совершает плоскопараллельное движение. Качение происходит без скольжения, следовательно, в данном случае точка касания колеса с неподвижной поверхностью – точка P – является МЦС. Определим угловую скорость колеса согласно формуле (3.10)

Зная расстояния от точек A, B и C до МЦС, можно найти их скорости по формуле (3.9)

Векторы скоростей точек колеса направлены перпендикулярно отрезкам, соединяющим их с МЦС (см. рис. 3.4,б). В соответствии с теоремой о проекциях скоростей двух точек тела на прямую, соединяющую эти точки, убеждаемся в правильности полученных результатов.

Перейдем к определению ускорений, для чего воспользуемся формулами (3.6) и (3.7). В качестве полюса выбираем точку O. Ускорение полюса равно нулю, так как эта точка движется равномерно и прямолинейно. Поэтому ускорения точек будут равны их ускорениям во вращательном движении вокруг полюса. Например, для точки А

.

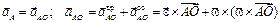
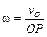
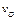
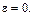
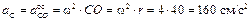
Дифференцируя по времени выражение и учитывая, что OP = const и = const, получим Таким образом, ускорения всех точек, включая МЦС, состоят из осестремительных ускорений во вращении вокруг полюса О

;

и направлены от соответствующих точек к полюсу (см. рис 3.4,в).

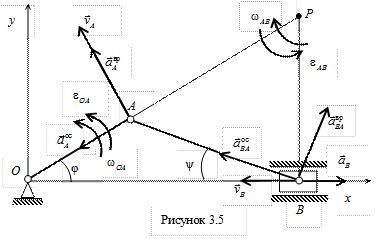
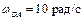
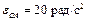
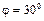
Пример 2. Кривошип ОА кривошипно-ползунного механизма, приведенного на рис. 3.5, вращается вокруг неподвижной оси с угловой скоростью и угловым ускорением . Положение механизма определяется углом .

Найти угловую скорость и угловое ускорение шатуна АВ, а также скорость и ускорение ползуна B, если длина кривошипа ОА = 10 см, а длина шатуна АВ = 30 см.

Вначале определим скорость точки А кривошипа

Затем, зная направления скоростей точек А и В, найдем положение МЦС на пересечении перпендикуляров к скоростям этих точек – точку P. Для определения угловой скорости шатуна 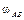и скорости точки В находим длины отрезков, соединяющих точки А и В с МЦС. Из теоремы синусов следует, что

Вычислим длины отрезков:

.

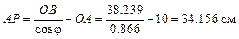
Теперь найдем искомые величины:

Определим ускорение точки В и угловое ускорение шатуна АВ. Здесь надо иметь в виду, что расстояние от точки А до МЦС не является постоянным и зависит от положения механизма, т.е. от времени. Поэтому продифференцировать по времени угловую скорость шатуна не представляется возможным. Поступим следующим образом. Для нахождения ускорения точки В воспользуемся векторным равенством (3.6)

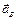
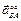
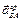
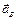
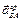
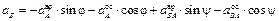
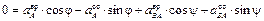
и спроецируем его на оси координат xOy (см. рис. 3.5). При этом учтем, что вектор лежит на прямой ОВ, так как точка В движется прямолинейно, вектор направлен к полюсу А, а вектор перпендикулярен ему. Получим два алгебраических уравнения для определения величин и направлений ускорений и (вначале направляем искомые векторы произвольно):

;

.

Предварительно вычислим составляющие ускорения согласно формулам (3.7):

– из 2-го уравнения

– из 1-го уравнения

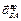
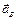
Знаки показывают, что направление ускорения совпадает с принятым, а направление – противоположно направлению, указанному на рис. 3.5. Зная ускорение , можно найти угловое ускорение шатуна

Вопросы для самоконтроля

1. Какое движение твердого тела называют плоскопараллельным?

2. На какие простейшие движения можно разложить плоскопараллельное движение?

3. Какие уравнения описывают плоскопараллельное движение?

4. Как определяют скорость произвольной точки плоской фигуры, если известна скорость полюса?

5. Какую точку плоской фигуры называют мгновенным центром скоростей (МЦС)?

6. Как распределены скорости точек тела по отношению к МЦС?

7. Какие существуют способы определения положения МЦС?

8. Как определяют ускорения произвольных точек тела, совершающего плоскопараллельное движение?

🎬 Видео

Урок 88 (осн). Линейная скорость точки на вращающемся телеСкачать

Центростремительное ускорение. 9 класс.Скачать

Определение скоростей при движении точек колесаСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Мгновенный центр скоростейСкачать

Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать

Мгновенная скорость (видео 6)| Векторы. Прямолинейное движение | ФизикаСкачать

Урок 8. Векторные величины. Действия над векторами.Скачать

Качение колеса без проскальзывания. Лекция 2-3Скачать

Физика: Понятие Вектор, Вектор СкоростиСкачать

Скорости точек плоской фигурыСкачать