Векторы начало и конец которого не совпадают (7 видео)

Вектор: определение и основные понятия

Содержание

Определение вектора
Обозначение вектора
Длина вектора
Нулевой вектор
Коллинеарные вектора
Сонаправленные вектора
Противоположно направленные вектора
Компланарные вектора
Равные вектора
Единичный вектор
Вектор. Виды векторов.
Векторы начало и конец которого не совпадают
🌟 Видео

Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Определение вектора

Векторы начало и конец которого не совпадают

рис. 1

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Обозначение вектора

Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Длина вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Нулевой вектор

Нулевой вектор обычно обозначается как 0 .

Длина нулевого вектора равна нулю.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Коллинеарные вектора

рис. 2

Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Сонаправленные вектора

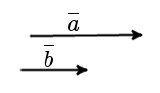рис. 3

Видео:№775. Начертите два неколлинеарных вектора р и q , начала которых не совпадаютСкачать

Противоположно направленные вектора

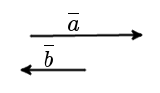рис. 4

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Компланарные вектора

рис. 5

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Равные вектора

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

Видео:№738. Отметь точки A, B и С не лежащие на одной прямой начертите все нулевые векторы началоСкачать

Единичный вектор

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Скалярное произведение векторов. 9 класс.Скачать

Вектор. Виды векторов.

Вектор — в самом элементарном случае это математический объект, который характеризуется

величиной и направлением.

В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая

из его граничных точек является началом, а какая — концом.

У вектора есть длина и определенное направление. Графически вектора изображаются как

направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.

Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Как видно на рисунке, начало отрезка – это точка А, концом отрезка является

точка В, а непосредственно вектор обозначен через . У направления

вектора существенное значение, если переместить стрелку на другую

сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора

удобно сравнивать с движением физического тела: подумайте, ехать на

рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть

разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.

Виды векторов.

Единичным называется вектор, длина которого равна 1.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.

У такого вектора конец и начало совпадают.

Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой

или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются

сонаправленными векторами только тогда, когда их направления

соответствуют друг другу: a↑↑b

Противоположно направленные вектора – два коллинеарных вектора

a и b называются противоположно направленными векторами, только

когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной

плоскости или те, которые лежат на общей плоскости.

В любое мгновение существует плоскость одновременно параллельную

двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на

одной либо параллельных прямых и их направления и длины одинаковые.

То есть, такой вектор можно перенести параллельно ему в каждое место

Таким образом, два вектора равны, если они коллинеарные, сонаправленые

и имеют одинаковые длины:

Для координатного представления векторов огромное значение

оказывает понятие проекции вектора на ось (направленную

прямую).

Проекция вектора — это длина отрезка, который образуется

проекциями точек начала и конца вектора на заданную прямую,

при этом проекции добавляется знак “+”, но когда направление

проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция

вектора на ось, которая перпендикулярна ему = 0.

Когда работают с векторами, зачастую вводят так называемую

декартову систему координат и уже в этой системе находят

координаты вектора по базисным векторам.

Разложение по базису геометрически можно показать проекцией

вектора на координатные оси. Когда известны координаты начала и

конца вектора, то координаты данного вектора получают вычитая

из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как , соответственно

осям x, y, z. Исходя из этого, вектор можно записать в таком виде:

Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование

из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,

кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только

те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).

Видео:№777. Начертите два неколлинеарных вектора р и q , начала которых не совпадают.Скачать

Векторы начало и конец которого не совпадают

1. Основные определения

Удивительно, но с векторными величинами разной природы (перемещением, скоростью, силой, импульсом и др.) можно работать в значительной мере единообразно — как с геометрическими объектами — геометрическими векторами, или просто векторами, хотя есть и нюансы (см. ниже).

Вектор представляет собой направленный отрезок прямой, для которого определены правила (законы) сложения с другими векторами, правило вычитания векторов, правило умножения вектора на число, скалярное произведение двух векторов и некоторые другие операции.

Стрелка компаса — не вектор, т. к. для неё нет таких операций.

Мы будем рассматривать векторы на плоскости и в соответствии со сложившейся традицией обозначать их латинскими буквами со стрелками наверху, например: `vec v`, `vec F`, `vec a`, `vec b` и т. п. Часто в целях экономии используют упрощённое обозначение — букву с чертой, например, `bar v` или `bar F`.

Одну из граничных точек вектора называют его началом, а другую — концом. Направление вектора задаётся от начала к концу, причём на чертеже конец вектора отмечают стрелкой. Начало вектора называют также точкой его приложения. Если точка `A` является началом вектора `vec a`, то мы будем говорить, что вектор `vec a` приложен в точке `A` (рис. 2).

Число, выражающее длину направленного отрезка, называют модулем вектора и обозначают той же буквой, что и сам вектор, но без стрелки наверху, например: модулем вектора `vec v` является число `v`. Часто для обозначения модуля вектора прибегают к помощи знака абсолютной величины и пишут, например, `|vec v|` или `|vec F|`.

Вектор называется нулевым, если его начало и конец совпадают. Нулевой вектор не имеет определённого направления и его длина (модуль) равна нулю.

Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Так, например, на рис. 3 векторы `vec a`, `vec b` и `vec c` коллинеарны.

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.

На рис. 4 слева изображены неравные векторы `vec a` и `vec f`, `vec g` и `vec h`, а справа — равные векторы `vec p` и `vec q`. Точка приложения геометрического вектора `vec a` может быть выбрана произвольно. Мы не различаем двух равных векторов, имеющих разные точки приложения и получающихся один из другого параллельным переносом. В соответствии с этим векторы, изучаемые в геометрии, называют свободными (они определены с точностью до точки приложения).

В физике точка приложения вектора иногда имеет принципиальное значение. Достаточно вспомнить рычаг: две равные по модулю силы, направленные в одну и ту же сторону, производят на рычаг разное действие, если плечи сил не равны друг другу. И всё же сами силы равны друг другу! Бывают и случаи, когда вектору трудно приписать конкретную точку приложения. Например, если одна система отсчёта движется относительно другой со скоростью `vec v`, то какой точке приписать эту скорость? Всем точкам движущейся системы!

2. Сложение двух векторов.

Пусть даны два произвольных вектора `vec a` и `vec b` (рис. 5а).

Для нахождения их суммы нужно перенести вектор `vec b` параллельно самому себе так, чтобы его начало совпало с концом вектора `vec a`. Тогда вектор, проведённый из начала вектора `vec a` в конец перенесённого вектора `vec b`, и будет являться суммой `vec a` и `vec b`. На рис. 5б — это вектор `vec c`.

Описанное правило есть просто определение суммы векторов. Как и в случае с числами, сумма векторов не зависит от порядка слагаемых, и поэтому можно записать

Приведённое выше правило геометрического сложения векторов называется правилом треугольника .

Сумма векторов может быть найдена и по правилу параллелограмма. В этом случае параллельным переносом нужно совместить начала векторов `vec a` и `vec b` и построить на них, как на сторонах, параллелограмм. Тогда сумма `vec a` и `vec b` будет представлять собой диагональ этого параллелограмма, конкретно — суммой `vec a` и `vec b` будет вектор, начало которого совпадает с общим началом векторов `vec a` и `vec b` конец расположен в противоположной вершине параллелограмма, а длина равна длине указанной диагонали (рис. 5в).

Оба способа сложения дают идентичный результат и одинаково часто применяются на практике. Когда речь идёт о нахождении суммы трёх и более векторов, часто последовательно используют правило треугольника. Поясним сказанное.

3. Сложение трёх и более векторов.

Пусть нужно сложить три вектора `vec a`, `vec b` и `vec d` (рис. 6).

Для этого по правилу треугольника сначала находится сумма любых двух векторов, например `vec a` и `vec b`, потом полученный вектор `vec c = vec a + vec b` по тому же правилу складывается с третьим вектором `vec d`. Тогда полученный вектор `vec f = vec c + vec d` и будет представлять собой сумму трёх векторов `vec a`, `vec b` и `vec d`: `vec f = vec a + vec b + vec d`. Как и в случае с двумя векторами, порядок слагаемых не влияет на конечный результат.

Чтобы упростить процесс сложения трёх и более векторов, обычно не находят промежуточные суммы типа `vec c = vec a + vec b`, а применяют правило многоугольника: параллельными переносами из конца первого вектора откладывают второй, из конца второго — откладывают третий, из конца третьего — четвёртый и т. д.

Так, на рис. 7 вектор `vec g` представляет собой сумму векторов `vec a`, `vec b`, `vec d`, `vec e`, найденную по правилу многоугольника: `vec g = vec a + vec b + vec d + vec e`.

Не всякая векторная сумма может иметь физический смысл. Не всякие величины вообще имеет смысл складывать. Так, например, бессмысленно говорить, что, если у меня температура `36,6^@` и у вас тоже `36,6^@`, то вместе у нас температура `73,2^@`, хотя складывать температуры (числа) никто не запрещает. Всё же чаще всего сумма температур представляет собой никому не нужную величину; она редко входит в какие-либо уравнения (входит почти случайно).

Иное дело – с массой. Если система состоит из тел с массами `m_1`, `m_2`, `m_3` и т. д., то масса всей системы равна `m = m_1 + m_2 + m_3 + ` и т. д. (Если на лифте написано, что максимальный груз, перевозимый лифтом, равен `500` кг, то перед входом в лифт нужно убедиться, что сумма масс вносимых в лифт грузов не превышает `500` кг.) Говорят, что масса – есть аддитивная величина (от английского слова add – добавлять, прибавлять, складывать). А вот температура – не аддитивная величина.

Сила есть аддитивная векторная величина. Если к телу в точке (или к системе тел в разных точках!) приложены силы `vec(F_1)`, `vec(F_2)`, `vec(F_3)` и т. д., то сумма векторов сил `vec(F_1) + vec(F_2) + vec(F_3) + . ` есть осмысленная и даже очень нужная величина. Например, в условиях равновесия тела сумма всех приложенных к нему сил `vec(F_1) + vec(F_2) + vec(F_3) + . = 0`, даже если силы приложены в разных точках тела. Причём это относится не только к твёрдым телам. Если нитка подвешена за два конца к двум гвоздям, а в промежутке перекинута еще через какие-нибудь гвозди, то сначала нужно найти силы со стороны каждого из гвоздей и силу со стороны Земли (силу тяжести) `vec F_1`, `vec(F_2)`, `vec(F_3)`, `…`; при этом говорят, что к нитке приложена сумма сил `vec(F_1) + vec(F_2) + vec(F_3) + . `; в условиях равновесия эта сумма будет равна нулю.

Не так со скоростями. Если система состоит из двух частиц, имеющих в некоторый момент времени скорости `vec(v_1)` и `vec(v_2)`, то это не означает, что в этот момент вся система обладает скоростью равной векторной сумме `vec(v_1) + vec(v_2)`. Никто не запрещает складывать векторы скорости разных частиц; но с точки зрения физики вектор `vec(v_1) + vec(v_2)` ничему приписать нельзя. В этом смысле скорость — не аддитивная величина. Суммой скоростей (векторной суммой) интересуются, когда одно движение накладывается на другое (например, Земля вращается вокруг Солнца, но вместе с Солнцем движется вокруг центра Галактики). А вот сумма скоростей отдельных частиц системы (например, сумма скоростей звезд в Галактике) физического интереса не представляет.

Родственная скорости величина, с которой вы еще не раз встретитесь в курсе физики, импульс материальной точки, равный произведению массы на скорость, `vec p = m vec v` снова — величина аддитивная.

В последнем равенстве мы встречаемся с умножением вектора на скаляр. Поясним эту процедуру.

4. Умножение вектора на скаляр.

Произведением вектора `vec a` на число `k` называют новый вектор `vec b = k vec a`, коллинеарный вектору `vec a`, направленный в ту же сторону, что и вектор `vec a`, если `k > 0`, и в противоположную сторону, если `k