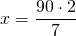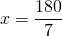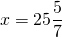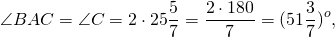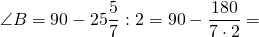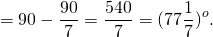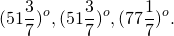Биссектриса угла при основании треугольника (5 видео)

Биссектриса угла при основании треугольника

Биссектриса угла при основании равнобедренного треугольника равна его стороне. Найти углы данного треугольника.

Дано : ∆ ABC,

2) Рассмотрим треугольник AFC.

Так как AF=AC, треугольник AFC — равнобедренный с основанием FC.

Следовательно, у него углы при основании равны:

По теореме о сумме углов треугольника

Таким образом, ∠BAC=∠C=2∙36=72º.

В условии задаче не указано, которой из сторон равна биссектриса треугольника — боковой или основанию. Мы рассмотрели вариант, когда биссектриса равна основанию. А может ли биссектриса угла при основании равняться боковой стороне?

Предположим, AF=AB, тогда ∠B=∠AFB.

Найдем углы при основании равнобедренного треугольника ABF

Эта же задача может быть сформулирована несколько иначе.

Биссектриса угла при основании равнобедренного треугольника пересекает боковую сторону под углом, равным углу при основании. Найти углы данного треугольника.

Содержание

Определение и свойства биссектрисы угла треугольника
Определение биссектрисы угла треугольника
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Пример задачи
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
💥 Видео

Видео:#194 БИССЕКТРИСА УГЛА // ПРИ ОСНОВАНИИСкачать

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Видео:21 Биссектриса угла при основании равнобедренного треугольника (повторение)Скачать

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Видео:Построение биссектрисы угла. 7 класс.Скачать

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

CD – внутренняя биссектриса ∠ACB;
CE – биссектриса угла, смежного с ∠ACB;
∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Видео:№684. Биссектрисы углов при основании АВ равнобедренного треугольника ABC пересекаются в точке М.Скачать

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Видео:Построение биссектрисы углаСкачать

Please wait.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

We are checking your browser. mathvox.ru

Видео:Биссектриса углаСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6dc014075d9f1654 • Your IP : 85.95.188.35 • Performance & security by Cloudflare