На комплексной плоскости (рис. 3.2) вектор представляют комплексным числом соответственно в алгебраической, тригонометрической и показательной формах:
где А = у>а 2 +b 2 , tga = -.
Рис. 3.2. Изображение комплексных величин на комплексной плоскости
Принимая а = со? + (р, получим
Таким образом, косинусоидально изменяющийся ток можно представить как вещественную часть комплексного числа:
При изменении времени t вектор Ime^ ot+ ^ будет вращаться на комплексной плоскости против часовой стрелки. При этом гармонический ток будет равен проекции этого вращающегося вектора на ось +1. Если возникает необходимость суммировать два гармонических тока
то их целесообразно изобразить двумя вращающимися векторами, представив их также и в комплексной форме (рис. 3.3), затем определить их сумму в комплексной форме
и взять вещественную часть от полученного комплексного числа ц + i2 = = Rе[1те^ + ^]. На графике это соответствует геометрической сумме двух векторов.
Рис. 33. Суммирование комплексных величин
Отметим, что при изменении времени t все векторы будут поворачиваться, не изменяя взаимного положения друг относительно друга. Это дает основание для того, чтобы в большинстве случаев не учитывать это вращение, а строить векторные диаграммы, учитывающие взаимное положение векторов при t = 0 = const. При этом каждый ток будет представлен комплексной амплитудой
Формально такие же значения будут присутствовать в уравнении напряжений, если левую и правую части разделить на Если еще разделить обе части этого уравнения на л/2, то вместо амплитуд будут действующие значения токов в комплексной форме записи. Их называют комплексами токов и обозначают с точкой вверху:
Аналогично можно записать комплексы напряжения и ЭДС:
Известен комплекс тока /= 3 + jA. Записать мгновенное значение тока. Решение. Записываем сначала комплекс тока в показательной форме
/ = vЗ 2 + А 1 е 83 = 5e j53 , затем умножаем его на 42е )Ы и берем вещественную часть:
Известны мгновенные значения напряжений ил = 311cos(314? + л/6), и2 = = 220cos(314? + я/4). Определить сумму напряжений.
Решение. Записываем комплексные амплитуды напряжений Um = 311с /30 , Um = 220с ;Ъ . Тогда комплексная амплитуда суммарного напряжения равна
Умножаем комплексную амплитуду на е ш * и берем вещественную часть: 
- Комплексные числа и операции с ними
- Комплексные числа
- Алгебраическая форма записи комплексных чисел
- Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
- Комплексно сопряженные числа
- Модуль комплексного числа
- Деление комплексных чисел, записанных в алгебраической форме
- Изображение комплексных чисел радиус-векторами координатной плоскости
- Аргумент комплексного числа
- Формула Эйлера. Экспоненциальная форма записи комплексного числа
- Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
- Извлечение корня натуральной степени из комплексного числа
- 💡 Видео
Видео:1.2 Комплексные числа и их представление векторами на комплексной плоскостиСкачать
Комплексные числа и операции с ними
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
Известно, что область определения некоторых функций на множестве вещественных чисел ограничена. Например функция определена для , аналогично можно вспомнить, что функция определена для 0″/>, а функция определена для .
Однако, ограниченная область определения функций на множестве вещественных чисел не означает, что , или не имеют смысла. Ограниченная область определения функций на множестве вещественных чисел говорит лишь о том, что не может быть представлено вещественным числом. Действительно, среди вещественных чисел не найти такого числа , квадрат которого был бы равен .
При решении квадратных уравнений часто возникает ситуация, когда дискриминант отрицательный. В этом случае это означает что парабола не пересекает прямую абсцисс ни в одной точке. Другими словами, корни квадратного уравнения не существуют среди вещественных значений и их также надо искать за пределами вещественных чисел.
Все бесконечное множество вещественных чисел можно представить в виде одной числовой прямой (смотри рисунок 1), на которой мы можем откладывать рациональные и иррациональные вещественные числа. Но на этой прямой нет числа , значит его надо искать вне числовой прямой. Таким образом мы должны расширить множество вещественных чисел до множества в котором значения , или уже не бессмысленны, а являются такими же обычными числами в этом расширенном множестве, как на множестве вещественных чисел.
Естественным расширением числовой прямой является плоскость, которую называют комплексной плоскостью. Числовая прямая вещественных чисел и ее расширение до комплексной плоскости показано на рисунке 1. Любая точка на комплексной плоскости определяет одно комплексное число. Например на рисунке 1 показано число .
Значение вещественного числа однозначно определяет его позицию на числовой прямой, однако для определения позиции на плоскости одного числа недостаточно.
Для «навигации» по комплексной плоскости вводятся две прямые и , которые пересекаются в начале координат. Прямая это числовая прямая, называемая реальной осью, на которой лежат все вещественные числа. Прямая называется мнимой осью и она перпендикулярна реальной оси . Оси и делят комплексную плоскость на четверти, как это показано на рисунке 1.
Любая точка комплексной плоскости задается двумя координатами и по осям и соответственно. При этом само комплексное число можно записать как , где называется реальной частью и задает координату точки комплексной плоскости на вещественной прямой , а называется мнимой частью и задает координату точки комплексной плоскости на мнимой оси .
Для того чтобы отделить одну координату от другой (реальную и мнимую части) вводят число , называемое мнимой единицей. Это так раз то число, которого не существует на множестве действительных чисел. Оно обладает особым свойством: . Тогда комплексное число может не только перемещаться по вещественной прямой вправо и влево, но и двигаться по комплексной плоскости потому что мы добавили ему слагаемое с мнимой единицей .
Мнимую единицу в математической литературе принято обозначать как , но в технике буква уже закреплена за обозначением электрического тока, поэтому чтобы избежать путаницы мы будем обозначать мнимую единицу буквой .
Если и , тогда число является действительным и располагается на реальной оси .
Если и , тогда число является чисто мнимым и располагается на мнимой оси .
Если и , тогда число располагается в одной из четвертей комплексной плоскости.
Представление комплексного числа как называют алгебраической формой записи. Если из начала координат комплексной плоскости к точке восстановить вектор (смотри рисунок 1), то можно вычислить длину этого вектора как
Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:
Видео:Изобразить область на комплексной плоскостиСкачать
Комплексные числа
 Алгебраическая форма записи комплексных чисел |
| Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
| Комплексно сопряженные числа |
| Модуль комплексного числа |
| Деление комплексных чисел, записанных в алгебраической форме |
| Изображение комплексных чисел радиус-векторами на координатной плоскости |
| Аргумент комплексного числа |
| Тригонометрическая форма записи комплексного числа |
| Формула Эйлера. Экспоненциальная форма записи комплексного числа |
| Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
| Извлечение корня натуральной степени из комплексного числа |
Видео:Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать
Алгебраическая форма записи комплексных чисел
Пусть x и y — произвольные вещественные числа.
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0) .
Комплексные числа, заданные парами (0, y) , называют чисто мнимыми числами .
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи .
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y) , записывается в виде
| z = x + i y . | (1) |
где использован символ i , называемый мнимой единицей .
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z .
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z .
Комплексные числа, у которых Im z = 0 , являются вещественными числами .
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами .
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Видео:Комплексные числа и их представление векторами на комплексной плоскостиСкачать
Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
| i 2 = – 1 . | (2) |
По этой причине
Видео:Векторная диаграмма токов на комплексной плоскости вручнуюСкачать
Комплексно сопряженные числа
Два комплексных числа z = x + iy и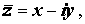 
у которых вещественные части одинаковые, а мнимые части отличаются знаком, называются комплексно сопряжёнными числами .
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения , обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
|  |
|  |
|  |
|  |
|  |
Видео:ТОЭ 26. Изображение синусоидально изменяющихся величин векторами на комплексной плоскости.Скачать
Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
|  |
|  |
|  |
|  |
Замечание . Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Видео:Линии и области на комплексной плоскостиСкачать
Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать
Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью , и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью , а ось ординат Oy – мнимой осью .
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Видео:Мнимые числа реальны: #6 Комплексная плоскость [Welch Labs]Скачать
![Мнимые числа реальны: #6 Комплексная плоскость [Welch Labs]](https://i.ytimg.com/vi/6Fh0C5ctMbA/0.jpg)
Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z .
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z .
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента , обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ , то мы можем найти вещественную и мнимую части по формулам
 | (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y , то модуль этого числа, конечно же, определяется по формуле
 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось | 0 | φ = 2kπ |  | |
| Первый квадрант |  |  |  | |
| Положительная мнимая полуось |  |  |  | |
| Второй квадрант |  |  |  | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры | |
| Расположение числа z | Первый квадрант |
| Знаки x и y | |
| Главное значение аргумента | |
| Аргумент | |
| Примеры | |
| Расположение числа z | Положительная мнимая полуось |
| Знаки x и y | |
| Главное значение аргумента | |
| Аргумент | |
| Примеры | |
| Расположение числа z | Второй квадрант |
| Знаки x и y | |
| Главное значение аргумента | |
| Аргумент | |
| Примеры | |
| Расположение числа z | Отрицательная вещественная полуось | ||||||||||
| Знаки x и y | Третий квадрант | ||||||||||
| Знаки x и y | Отрицательная мнимая полуось | ||||||||||
| Знаки x и y | Четвёртый квадрант | ||||||||||
| Знаки x и y | |||||||||||
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа .
Видео:Область на комплексной плоскости arg z = pi/2Скачать
Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
| cos φ + i sin φ = e iφ . | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r e iφ , | (7) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа .
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
или, что то же самое, числа e iφ , при любом значении φ равен 1.
Видео:10 класс, 33 урок, Комплексные числа и координатная плоскостьСкачать
Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 
и 
записанных в экспоненциальной форме, осуществляется по формулам
Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Видео:Построение областей по заданным условиямСкачать
Извлечение корня натуральной степени из комплексного числа
Пусть 
— произвольное комплексное число, отличное от нуля.
Корнем n — ой степени из числа z0 , где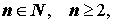 
называют такое комплексное число z = r e iφ , которое является решением уравнения
| z n = z0 . | (8) |
Для того, чтобы решить уравнение (8), перепишем его в виде
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна 2kπ , где k — произвольное целое число. По этой причине справедливы равенства
следствием которых являются равенства
 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
 | (10) |
причем на комплексной плоскости концы радиус-векторов zk при k = 0 , . , n – 1 располагаются в вершинах правильного n — угольника, вписанного в окружность радиуса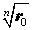 
с центром в начале координат.
Замечание . В случае n = 2 уравнение (8) имеет два различных корня z1 и z2 , отличающихся знаком:
Пример 1 . Найти все корни уравнения
то по формуле (10) получаем:
Пример 2 . Решить уравнение
Решение . Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:
💡 Видео
✓ Комплексные числа. Введение | Ботай со мной #039 | Борис ТрушинСкачать
Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Тригонометрическая форма комплексного числаСкачать
2. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числаСкачать
Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать
10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать
Аргумент комплексного числа. Часть 1Скачать
Комплексные числа в электротехникеСкачать
