2018-05-14 
Имеется очень длинный прямой соленоид с током $I$. Площадь поперечного сечения соленоида равна $S$, число витков на единицу длины — $n$. Найти поток вектора $vec$ через торец соленоида.
Используя задачу 7536, магнитное поле задается,
$B = frac mu_ nI left ( 1 — frac < sqrt<x^+ R^ > > right )$
В торце, $B = frac mu_ nI = frac B_$, где $B_ = mu_nI$,
это поле глубоко внутри соленоида. Таким образом,
$Phi = frac mu_ nIS = Phi_/2$, где $Phi = mu_nIS $
поток вектора $B$ через сечение глубоко внутри соленоида.
Видео:Теорема о циркуляции вектора магнитной индукции. Магнитный поток.Скачать

Вектора магнитной индукции через торец соленоида
| Магнитное поле соленоида |   |
Применим теорему о циркуляции вектора Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно (рис. 2.12), симметричные относительно такой плоскости витки создают поле, в котором вектор Из параллельности вектора Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13. Второй и четвёртый интегралы равны нулю, т.к. вектор Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда где Если отрезок 1–2 внутри соленоида, контур охватывает ток: где n – число витков на единицу длины, I – ток в соленоиде (в проводнике). Тогда магнитная индукция внутри соленоида:
Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри. Произведение nI – называется число ампер витков на метр. У конца полубесконечного соленоида, на его оси магнитная индукция равна:
Практически, если длина соленоида много больше, чем его диаметр, формула (2.7.1) справедлива для точек вблизи середины, формула (2.7.2) для точек около конца. Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке А, лежащей на оси соленоида, направлена вдоль оси (по правилу буравчика) и численно равна алгебраической сумме индукций магнитных полей создаваемых в точке А всеми витками. В этом случае имеем: · В точке, лежащей на середине оси соленоида магнитное поле будет максимальным:
где L – длина соленоида, R – радиус витков. · В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле
На рисунке 2.15 изображены силовые линии магнитного поля Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать  Вектора магнитной индукции через торец соленоидаПо длинному тонкому соленоиду течёт ток I. Как изменятся следующие физические величины, если увеличить радиус соленоида, оставляя без изменений число его витков и длину: модуль вектора индукции магнитного поля на оси соленоида, поток вектора магнитной индукции через торец соленоида, индуктивность соленоида. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А) Магнитная индукция внутри соленоида рассчитывается по формуле Б) Поток вектора магнитной индукции через торец соленоида В) Индуктивность соленоида Это задание выходит за рамки школьной программы. 🔥 ВидеоМагнитное поле соленоидаСкачать  Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать  магн поле внутри соленоидаСкачать  Поток вектора магнитной индукцииСкачать  2.3. Теорема о циркуляции вектора магнитной индукцииСкачать  Урок 271. Модуль вектора магнитной индукции. Закон АмпераСкачать  Опыты по физике. Магнитное поле соленоидаСкачать  Вектор магнитной индукции, принцип суперпозиции магнитных полейСкачать  Теорема Ампера о циркуляции магнитной индукции. Магнитное поле соленоида и тороида в вакууме.Скачать  Как магнитное поле назвали магнитной индукциейСкачать  Физика - Магнитное полеСкачать  Галилео. Эксперимент. Электромагнитная индукцияСкачать  Электродинамика | теорема о циркуляции магнитной индукции | 1Скачать 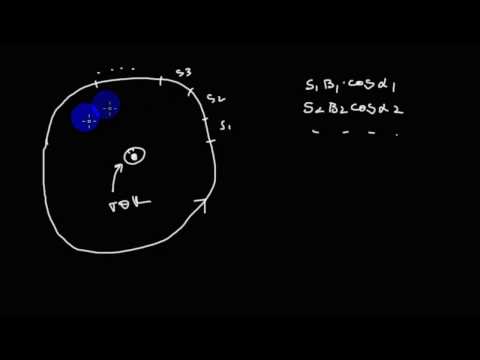 53. Теорема о циркуляции вектора индукцииСкачать  Магнитное поле. Вектор магнитной индукцииСкачать  Магнитное поле. Магнитная индукция | Физика 11 класс #1 | ИнфоурокСкачать  Доказательство теоремы о циркуляции вектора В - Дополнение-1 к лекции 7Скачать  Урок 171 (осн). Магнитное поле витка и катушки с токомСкачать  |



 для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).
для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).



 .
.
 – магнитная индукция на участке 1–2 – внутри соленоида,
– магнитная индукция на участке 1–2 – внутри соленоида,  – магнитная проницаемость вещества.
– магнитная проницаемость вещества.
 ,
, и
и  , т.е.
, т.е.  .
. ,
, ,
, ,
,