| Понятие матрицы |    |
Матрица представляет собой прямоугольную таблицу элементов, в качестве которых могут выступать числа, функции, символы, слова и так далее — при условии, что заданы определенные правила математических действий с этими элементами. Примеры матриц: | ||
| Матрицами называются массивы элементов, представленные в виде прямоугольных таблиц, для которых определены правила математических действий. Элементами матрицы могут являться числа, алгебраические символы или математические функции. Матричная алгебра имеет обширные применения в различных отраслях знания – в математике, физике, информатике, экономике. Например, матрицы используется для решения систем алгебраических и дифференциальных уравнений, нахождения значений физических величин в квантовой теории, шифрования сообщений в Интернете. Матрица обозначается одной из заглавных букв латинского алфавита, а набор ее элементов помещается в круглые скобки:
Представленная формулой (1) матрица A имеет m строк и n столбцов и называется m×n матрицей (“эм на эн матрицей”) или матрицей размера m×n. Строки матрицы нумеруются сверху вниз, а столбцы – слева направо. Рис. 1. Порядок нумерации строк и столбцов матрицы. Матричный элемент, расположенный на пересечении i-ой строки и j-го столбца, называется i,j-м элементом и записывается в виде ai j , а выражение A = || ai j || означает, что матрица A составлена из элементов ai j . Матрица Матрица Особую роль играют матрицы, у которых число строк совпадает с числом столбцов, то есть матрицы размера n×n. Такие матрицы называются квадратными При ссылке на квадратную матрицу достаточно указать ее порядок. Например, матрица третьего порядка имеет размер 3×3. Квадратная матрица порядка 1 отождествляется с единственным ее элементом. Содержание
Видео:Работа с массивами. Вектор столбцы и вектор строки 2. Урок 8Скачать  Знакомство с матрицамиПонятие и базовые операции. Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:
Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы. Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать  Что такое матрицаЕсли вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции. Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее. Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице. В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной. В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности. Видео:Матрицы и векторыСкачать  Простые операции с матрицамиВынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы. И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу. Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число. Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок. ⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица. Видео:4. Умножение матриц, примеры с решениемСкачать  Сложение и вычитание матрицЕсли в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу. Видео:Линал 2.6. Умножение матрицы на векторСкачать  Умножение матрицМатрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:
Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль. Видео:Основы МАТЛАБ.РАБОТА С МАССИВАМИ. ВЕКТОРЫ-СТОЛБЦЫ И ВЕКТОРЫ-СТРОКИСкачать  Что дальшеВ следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽 Видео:Собственные векторы и собственные значения матрицыСкачать  Умножение матрицИтак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу. Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений. Видео:Вектор-строка / Вектор-столбец / Ориентация вектора: Линейная алгебра для Data Science #datascienceСкачать  Согласованные матрицыОдна из важнейших характеристик матрицы — это её размер. Мы уже сто раз говорили об этом: запись $A=left[ mtimes n right]$ означает, что в матрице ровно $m$ строк и $n$ столбцов. Как не путать строки со столбцами, мы тоже уже обсуждали. Сейчас важно другое.
Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:
Кроме того, капитан очевидность как бы намекает, что квадратные матрицы одинакового размера $left[ ntimes n right]$ согласованы всегда.
Так вот: координаты — это тоже упорядоченные пары, которые составляются из чисел. Но ничто не мешает составить такую пару из матриц. Тогда можно будет сказать: «Упорядоченная пара матриц $left( A;B right)$ является согласованной, если количество столбцов в первой матрице совпадает с количеством строк во второй». Ну и что с того? Видео:Линейная алгебра, 2 урок, Умножение матрицСкачать  Определение умноженияРассмотрим две согласованные матрицы: $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$. И определим для них операцию умножения.
Обозначается такое произведение стандартно: $C=Acdot B$. По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет] У тех, кто впервые видит это определение, сразу возникает два вопроса:
Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами? Прежде всего заметим, что длинная строчка для расчёта $<_>$ (специально поставил точку с запятой между индексами, чтобы не запутаться, но вообще их ставить не надо — я сам задолбался набирать формулу в определении) на самом деле сводится к простому правилу:
Данный процесс легко понять по картинке: Ещё раз: фиксируем строку $i$ в первой матрице, столбец $j$ во второй матрице, перемножаем элементы с одинаковыми номерами, а затем полученные произведения складываем — получаем $<_>$. И так для всех $1le ile m$ и $1le jle k$. Т.е. всего будет $mtimes k$ таких «извращений».
Тогда их скалярным произведением будет именно сумма попарных произведений: По сути, в те далёкие годы, когда деревья были зеленее, а небо ярче, мы просто умножали вектор-строку $overrightarrow$ на вектор-столбец $overrightarrow$. Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше. Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц. Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать  Умножение квадратных матриц[left[ begin<*> 1 & 2 \ -3 & 4 \end right]cdot left[ begin<*> -2 & 4 \ 3 & 1 \end right]] Решение. Итак, у нас две матрицы: $A=left[ 2times 2 right]$ и $B=left[ 2times 2 right]$. Понятно, что они согласованы (квадратные матрицы одинакового размера всегда согласованы). Поэтому выполняем умножение: [begin & left[ begin<*> 1 & 2 \ -3 & 4 \end right]cdot left[ begin<*> -2 & 4 \ 3 & 1 \end right]=left[ begin<*> 1cdot left( -2 right)+2cdot 3 & 1cdot 4+2cdot 1 \ -3cdot left( -2 right)+4cdot 3 & -3cdot 4+4cdot 1 \end right]= \ & =left[ begin<*> 4 & 6 \ 18 & -8 \end right]. end] Задача 2. Выполните умножение: [left[ begin 1 & 3 \ 2 & 6 \end right]cdot left[ begin<*>9 & 6 \ -3 & -2 \end right]] Решение. Опять согласованные матрицы, поэтому выполняем действия:[] [begin & left[ begin 1 & 3 \ 2 & 6 \end right]cdot left[ begin<*> 9 & 6 \ -3 & -2 \end right]=left[ begin<*> 1cdot 9+3cdot left( -3 right) & 1cdot 6+3cdot left( -2 right) \ 2cdot 9+6cdot left( -3 right) & 2cdot 6+6cdot left( -2 right) \end right]= \ & =left[ begin 0 & 0 \ 0 & 0 \end right]. end] Как видим, получилась матрица, заполненная нулями Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2. В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач. Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать  Основные свойства матричного произведенияВ двух словах. Умножение матриц:
А теперь — всё то же самое, но более подробно. Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно. Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем: [left[ begin<*> 1 & 2 \ -3 & 4 \end right]cdot left[ begin<*> -2 & 4 \ 3 & 1 \end right]=left[ begin<*>4 & 6 \ 18 & -8 \end right]] Но если поменять матрицы местами, то получим совсем другой результат: [left[ begin<*> -2 & 4 \ 3 & 1 \end right]cdot left[ begin<*> 1 & 2 \ -3 & 4 \end right]=left[ begin -14 & 4 \ 0 & 10 \end right]] Получается, что $Acdot Bne Bcdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $left[ 2times 3 right]$ и $left[ 3times 5 right]$ вполне себе согласованы в указанном порядке, но те же матрицы $left[ 3times 5 right]$ и $left[ 2times 3 right]$, записанные в обратном порядке, уже не согласованы. Печаль.:(
Тем не менее, умножение матриц ассоциативно: [left( Acdot B right)cdot C=Acdot left( Bcdot C right)] Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше. В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $left[ ntimes n right]$. Множество всех таких матриц обозначается $<^>$ (т.е. записи $A=left[ ntimes n right]$ и [Ain <^>] означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.
[Acdot E=Ecdot A=A] Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули. Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно: Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:) Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться. Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных? Видео:Линейная зависимость и линейная независимость. ТемаСкачать  Случай прямоугольных матрицА ничего — всё то же самое, что и с квадратными. [left[ begin begin 5 \ 2 \ 3 \end & begin 4 \ 5 \ 1 \end \end right]cdot left[ begin<*> -2 & 5 \ 3 & 4 \end right]] Решение. Имеем две матрицы: $A=left[ 3times 2 right]$ и $B=left[ 2times 2 right]$. Выпишем числа, обозначающие размеры, в ряд: Как видим, центральные два числа совпадают. Значит, матрицы согласованы, и их можно перемножить. Причём на выходе мы получим матрицу $C=left[ 3times 2 right]$: [begin & left[ begin begin 5 \ 2 \ 3 \end & begin 4 \ 5 \ 1 \end \end right]cdot left[ begin<*> -2 & 5 \ 3 & 4 \end right]=left[ begin<*> 5cdot left( -2 right)+4cdot 3 & 5cdot 5+4cdot 4 \ 2cdot left( -2 right)+5cdot 3 & 2cdot 5+5cdot 4 \ 3cdot left( -2 right)+1cdot 3 & 3cdot 5+1cdot 4 \end right]= \ & =left[ begin<*> 2 & 41 \ 11 & 30 \ -3 & 19 \end right]. end] Всё чётко: в итоговой матрице 3 строки и 2 столбца. Вполне себе $=left[ 3times 2 right]$. Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение? Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.
Решение. Для начала запишем размеры матриц: [A=left[ 2times 4 right]; B=left[ 4times 2 right]; C=left[ 2times 2 right]] Получаем, что матрицу $A$ можно согласовать лишь с матрицей $B$, поскольку количество столбцов у $A$ равно 4, а такое количество строк только у $B$. Следовательно, можем найти произведение: [Acdot B=left[ begin<*> 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end right]cdot left[ begin<*> 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end right]=left[ begin<*>-10 & 7 \ 10 & 7 \end right]] Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений: [A cdot B=left[ 2times 4 right]cdot left[ 4times 2 right]=left[ 2times 2 right]] Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц. Какие ещё возможны варианты? Безусловно, можно найти $Bcdot A$, поскольку $B=left[ 4times 2 right]$, $A=left[ 2times 4 right]$, поэтому упорядоченная пара $left( B;A right)$ является согласованной, а размерность произведения будет: [B cdot A=left[ 4times 2 right]cdot left[ 2times 4 right]=left[ 4times 4 right]] Короче говоря, на выходе будет матрица $left[ 4times 4 right]$, коэффициенты которой легко считаются: [Bcdot A=left[ begin<*> 0 & 1 \ 2 & 0 \ 0 & 3 \ 4 & 0 \end right]cdot left[ begin<*> 1 & -1 & 2 & -2 \ 1 & 1 & 2 & 2 \end right]=left[ begin<*>1 & 1 & 2 & 2 \ 2 & -2 & 4 & -4 \ 3 & 3 & 6 & 6 \ 4 & -4 & 8 & -8 \end right]] Очевидно, можно согласовать ещё $Ccdot A$ и $Bcdot C$ — и всё. Поэтому просто запишем полученные произведения: [Ccdot A=left[ begin<*> 1 & 1 & 2 & 2 \ 1 & -1 & 2 & -2 \end right]] [Bcdot C=left[ begin<*>1 & 0 \ 0 & 2 \ 3 & 0 \ 0 & 4 \end right]] Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц. Но на этом история не заканчивается. Переходим к частным случаям умножения.:) Вектор-строки и вектор-столбцыОдной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.
— это матрица размера $left[ 1times n right]$, т.е. состоящая из одной строки и нескольких столбцов. [left[ begin<*> 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end right]cdot left[ begin<*> 1 \ 2 \ -1 \end right]] Решение. Перед нами произведение согласованных матриц: $left[ 3times 3 right]cdot left[ 3times 1 right]=left[ 3times 1 right]$. Найдём это произведение: [left[ begin<*> 2 & -1 & 3 \ 4 & 2 & 0 \ -1 & 1 & 1 \end right]cdot left[ begin<*> 1 \ 2 \ -1 \end right]=left[ begin<*> 2cdot 1+left( -1 right)cdot 2+3cdot left( -1 right) \ 4cdot 1+2cdot 2+0cdot 2 \ -1cdot 1+1cdot 2+1cdot left( -1 right) \end right]=left[ begin<*> -3 \ 8 \ 0 \end right]] Задача 6. Выполните умножение: [left[ begin<*> 1 & 2 & -3 \end right]cdot left[ begin<*> 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end right]] Решение. Опять всё согласовано: $left[ 1times 3 right]cdot left[ 3times 3 right]=left[ 1times 3 right]$. Считаем произведение: [left[ begin<*> 1 & 2 & -3 \end right]cdot left[ begin<*> 3 & 1 & -1 \ 4 & -1 & 3 \ 2 & 6 & 0 \end right]=left[ begin<*>5 & -19 & 5 \end right]] На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:) Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном). Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока. Видео:Умножение матрицСкачать  Возведение матрицы в степеньСреди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени. Такие произведения всегда согласованы: [Acdot A=left[ ntimes n right]cdot left[ ntimes n right]=left[ ntimes n right]] И обозначаются точно так же, как и обычные степени: На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:
Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат: [begin & <<left[ begin1 & 1 \ 0 & 1 \end right]>^>=left[ begin 1 & 1 \ 0 & 1 \end right]cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left[ begin<*> 1cdot 1+1cdot 0 & 1cdot 1+1cdot 1 \ 0cdot 1+1cdot 0 & 0cdot 1+1cdot 1 \end right]= \ & =left[ begin<*> 1 & 2 \ 0 & 1 \end right] end] [begin & <<left[ begin1 & 1 \ 0 & 1 \end right]>^>= <<left[ begin1 & 1 \ 0 & 1 \end right]>^>cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left[ begin<*> 1 & 2 \ 0 & 1 \end right]cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left[ begin<*> 1 & 3 \ 0 & 1 \end right] end] Ответ: $left[ begin1 & 3 \ 0 & 1 \end right]$. Задача 8. Возведите матрицу в указанную степень: Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко: [begin & <<left[ begin1 & 1 \ 0 & 1 \end right]>^>= <<left[ begin1 & 1 \ 0 & 1 \end right]>^>cdot <<left[ begin1 & 1 \ 0 & 1 \end right]>^>cdot <<left[ begin1 & 1 \ 0 & 1 \end right]>^>cdot left[ begin 1 & 1 \ 0 & 1 \end right]= \ & =left( left[ begin 1 & 3 \ 0 & 1 \end right]cdot left[ begin 1 & 3 \ 0 & 1 \end right] right)cdot left( left[ begin 1 & 3 \ 0 & 1 \end right]cdot left[ begin 1 & 1 \ 0 & 1 \end right] right)= \ & =left[ begin 1 & 6 \ 0 & 1 \end right]cdot left[ begin 1 & 4 \ 0 & 1 \end right]= \ & =left[ begin 1 & 10 \ 0 & 1 \end right] end] Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно. Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить: Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности. В общем, не ищите высший смысл там, где его нет. В заключение рассмотрим возведение в степень матрицы большего размера — аж $left[ 3times 3 right]$.
Решение. Не будем искать закономерности. Работаем «напролом»: [ <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^>= <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^>cdot left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]] Для начала возведём эту матрицу в квадрат: [begin & <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^>=left[ begin 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]cdot left[ begin 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]= \ & =left[ begin<*> 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end right] end] Теперь возведём в куб: [begin & <<left[ begin0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]>^>=left[ begin<*> 2 & 1 & 1 \ 1 & 2 & 1 \ 1 & 1 & 2 \end right]cdot left[ begin 0 & 1 & 1 \ 1 & 0 & 1 \ 1 & 1 & 0 \end right]= \ & =left[ begin<*> 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end right] end] Вот и всё. Задача решена. Ответ: $left[ begin 2 & 3 & 3 \ 3 & 2 & 3 \ 3 & 3 & 2 \end right]$. Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:) На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители. Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения. 💥 Видео#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать  Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать  numpy01 - Вектор строки и вектор столбцы#shortsСкачать  Линейная алгебра, 6 урок, Ранг матрицыСкачать  Собственные значения и собственные векторы матрицы (4)Скачать  Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать  Собственные значения и собственные векторыСкачать  |



 размера 1×n называется строчной или вектор-строкой.
размера 1×n называется строчной или вектор-строкой. размера n×1 называется столбцевой или вектор-столбцом. Для краткости вектор-строку и вектор-столбец обычно называют просто векторами.
размера n×1 называется столбцевой или вектор-столбцом. Для краткости вектор-строку и вектор-столбец обычно называют просто векторами. Общая схема матрицы
Общая схема матрицы  Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три
Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре
Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре  Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений
Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений Пример умножения матрицы на число
Пример умножения матрицы на число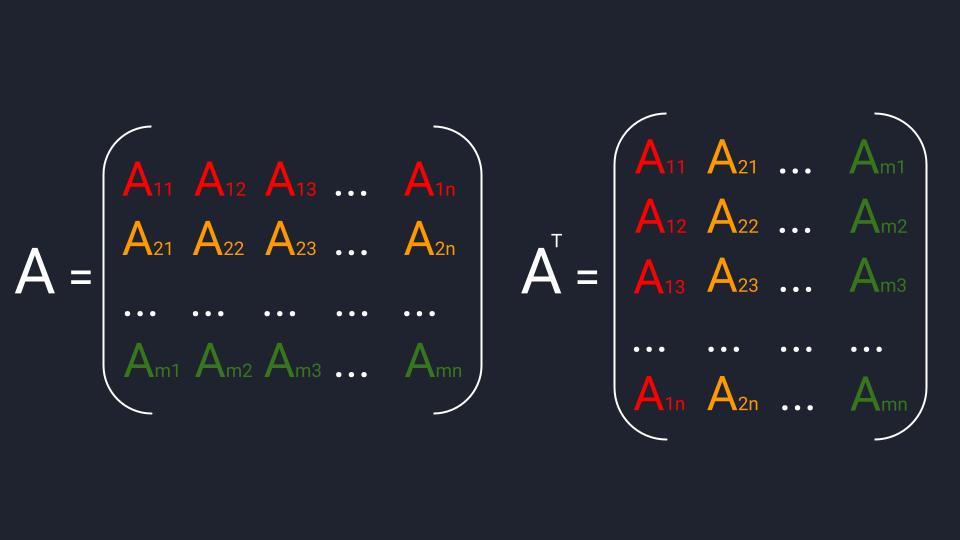 Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы
Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы  Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т»
Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» 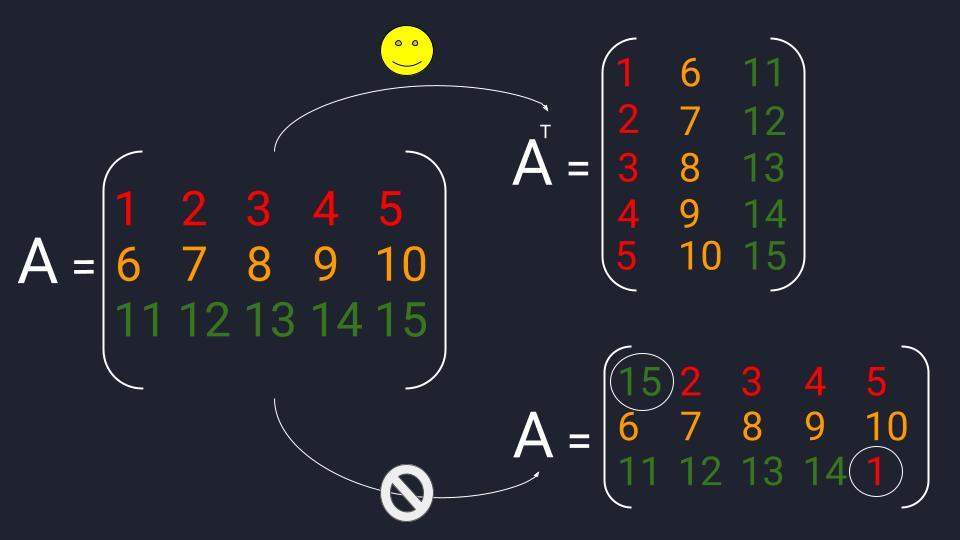 Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил
Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами
Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами  Пример вычитания двух матриц
Пример вычитания двух матриц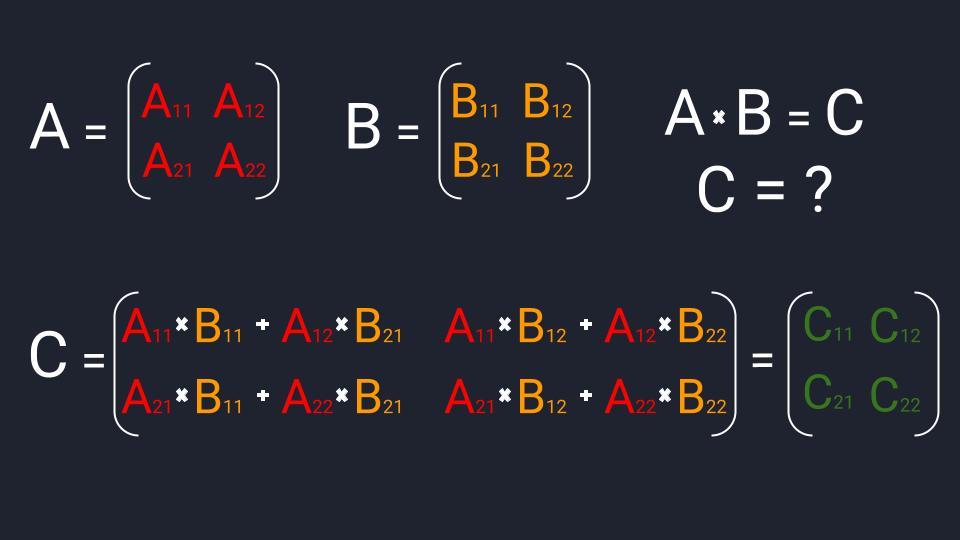 Формула умножения матриц
Формула умножения матриц  Пример умножения квадратных матриц размерностью 2×2
Пример умножения квадратных матриц размерностью 2×2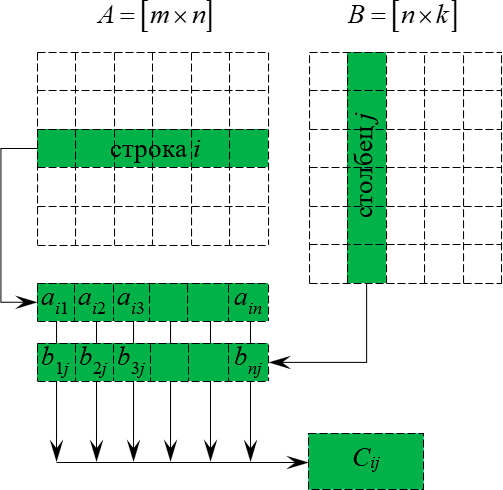 Схема перемножения двух матриц
Схема перемножения двух матриц