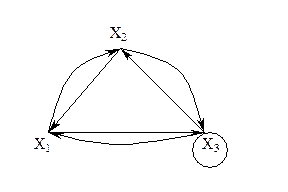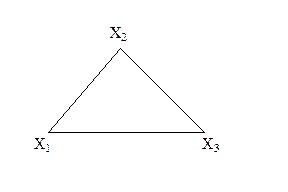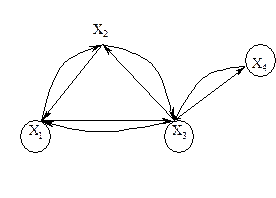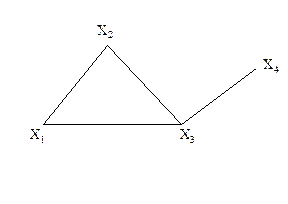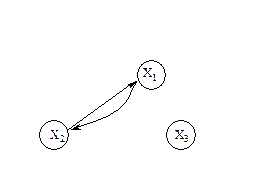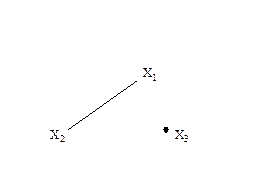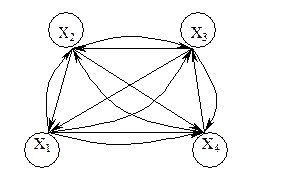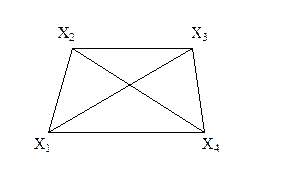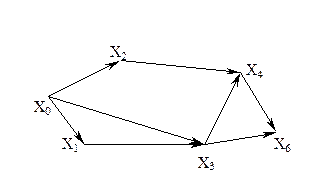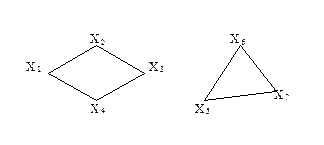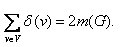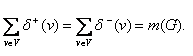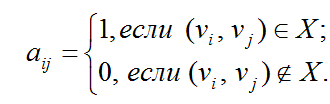Степень вершины графа. Число ребер графа.

Теория графов

Графы

Бинарное отношение на конечном множестве X есть ориентированный конечный граф (орграф) RÍX 2 . Таким образом, всякий орграф определяется множествами:

X=<X₁,X₂,…,X_n> – множеством вершин графа и множеством упорядоченных пар (кортежей)

Общепринято обозначать орграфы в виде

X – множество вершин орграфа;

U – множество дуг орграфа, или в виде

ГX = <Гx₁,Гx₂,…,Гx_n> – множество образов элементов множества X, т.е. отображение X в X, понимая термин отображения как точечно-множественное отображение.

Наряду с орграфами в приложениях рассматриваются неориентированные графы. Неориентированный граф является частным случаем орграфа, в котором для каждой дуги , т.е. бинарное отношение R обладает свойством симметрии. Если, кроме того, бинарное отношение R обладает свойством рефлексивности, то соответствующий ему ориентированный граф есть орграф-толерантность, содержащий дуги типа петля для всех вершин графа.

При геометрической реализации неориентированного графа вместо двух дуг и , соединяющих вершины X_i и X_j, употребляется одно ребро (X_i,X_j), не имеющее ориентации. На рис. 3.1.1 приведены геометрические реализации орграфов (слева) и их неориентированных аналогов – неориентированных графов (справа). G(X,U), если X’ÍX; U’ÍU, т.е. подграф G’ получим из графа G, если уберем какое-либо число вершин или ребер (дуг).

Две вершины графа называются смежными, если они соединены с началом другой.

Дуги называются смежными, если конец одной из них совпадает с началом другой.

Некоторая последовательности смежных дуг называется путем, а последовательность смежных ребер называется цепью.

Замкнутый путь называется контуром, а замкнутая цепь – циклом.

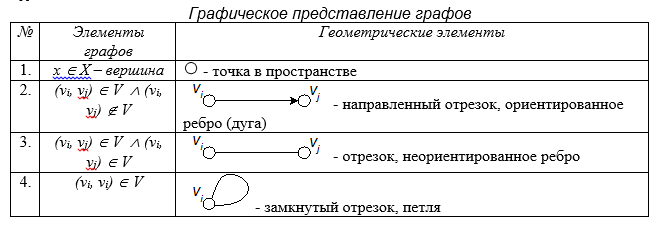
Сформулированные определения удобно представить в виде следующей таблицы:

Ориентированный граф	Неориентированный граф
Дуга	Ребро
Путь	Цепь
Контур	Цикл

Рассмотрим еще некоторые определения, которые нам понадобятся в дальнейшем. Пусть (цепь) называется элементарным, если он проходит через вершины графа по одному разу.

Путь (цепь) называется простым, если он проходит через дуги графа по одному разу. В противном случае путь (цепь) называется составным. Аналогично определяются и простые контуры и циклы.

Цепь (цикл) называется гамильтоновой, если она проходит через все вершины графа по одному разу, т.е. элементарная цепь, проходящая через все вершины графа, есть гамильтонова цепь.

Цепь (цикл) называется эйлеровой, если она проходит через все ребра по одному разу, т.е. простая цепь (цикл), содержащая все ребра графа есть эйлерова цепь (цикл).

Аналогично определяются гамильтоновы и эйлеровы путь и контуры.

Симметричный граф Неориентированный граф

Граф-толерантность Неориентированный граф

Граф-декартово произведение Неориентированный полный граф

(с полным насыщением)

Степень вершины графа. Число ребер графа.

Вершина X_i называется инцидентной дуге (ребру) графа, если она является началом или концом этой дуги (ребра).

Степенью вершины графа называют число дуг (ребер), инцидентных данной вершине. Степень обозначается P(X_i).

Для ориентированного графа различают полустепень захода P + — число дуг, входящих в данную вершину, и полустепень исхода P — — число дуг, выходящих из данной вершины. Степень вершины ориентированного графа составит сумма полустепеней исхода и захода.

Если для некоторой вершины ориентированного графа полустепень захода некоторой вершины P + =0 и при этом полустепень исхода P — ¹0, то вершина называется входом графа.

Если для некоторой вершины ориентированного графа P — =0, а P + ¹0, то вершина называется выходом графа.

Граф, изображенный на рис. 3.1.2, имеет один вход – вершину X₀

Число ребер графа N связано со степенями его вершин следующим соотношением:

N= ,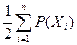

где n – число вершин графа. Отсюда следует справедливость следующих утверждений:

1) Сумма степеней вершин любого графа четна;

2) Для любого графа число вершин, имеющих нечетные степени, четно;

3) Для однородного графа, т.е. графа, все степени вершин которого одинаковы и равны r, N= ;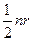

4) Для полного графа, т.е. графа, в котором каждая пара вершин соединена ребром или дугой, P(X_i)=n-1, а N= .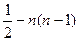

Некоторой противоположностью полному графу является нуль-граф, не имеющий ребер или дуг и состоящий из изолированных вершин. Очевидно, степени верши нуль-графа равны 0.

Связность

Граф называется связным, если множество его вершин нельзя разбить на два или более подмножеств так, чтобы ни одна вершины одного подмножества не отображалась в вершину другого. В противном случае граф называется несвязным. Число подмножеств всех вершин графа, называется числом компонент связности для несвязного графа.

Существует другое определение связности графа. Граф называется связным, если две любые его вершины можно соединить цепью. Граф (рис. 3.1.3) является несвязным с двумя компонентами.

Ребро графа называется перешейком, или связующей линией, если его удаление приводит к тому, что граф становится несвязным. На рис. 3.1.4 изображены три связных неориентированных графа, причем граф 1 не имеет ни одного перешейка, 2 содержит один перешеек (отмечен жирной линией), граф 3 целиком состоит из одних перешейков. Такой граф (3) называется деревом.

Содержание

Ориентированные графы в GeoGebra? Степени вершин ориентированного графа
1. Графы. Основные понятия и определения. Матрицы смежностей вершин графов. Матрицы инциденций графов и орграфов. Степени вершин и полустепени исхода и захода. Основные типы графов.
Основные понятия и определения.
Степени вершин и полустепени исхода и захода.
Матрицы смежностей и инциденций вершин графов и орграфов.
Основные типы графов.
🔥 Видео

Ориентированные графы в GeoGebra? Степени вершин ориентированного графа

Описание: Наводим мышку на стрелочку внизу, она становится красной, нажимаем на нее правой кнопкой мыши, открывается скрытая вкладка, выбираем в ней Вектор по двум точкам

Дата добавления: 2014-08-04

Размер файла: 206.91 KB

Работу скачали: 18 чел.

Поделитесь работой в социальных сетях

Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск

Ориентированные графы в GeoGebra ? Степени вершин ориентированного графа.

Пусть теперь множество E = представляет собой некоторое бинарное отношение на множестве V ( E  V  V ). Тогда пара множеств V и E называется ориентированным графом ( орграфом ) Γ ( V , E ) с множеством вершин V и множеством ребер E . Другими словами, на графе Γ задана ориентация, у каждого ребра есть направление.

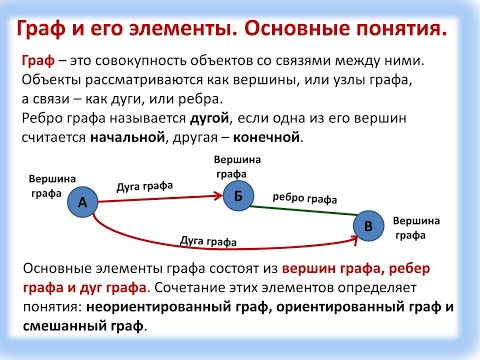
Ребро ориентированного графа называется дугой . Для дуги e k =( v i , v j ) вершина v i называется начальной , а v j  конечной . Иными словами, ребро e k выходит из вершины v i и заходит в вершину v j . Как и в случае неориентированного ребра, дуга e k инцидентна вершинам v i и v j , а вершины v i и v j инцидентны дуге e k . Вершины v i и v j также называют смежными . На диаграмме дуги изображаются стрелочками.

Для вершин ориентированного графа определяются две локальные степени:  1 ( v ) — число рёбер с началом в вершине v (количество выходящих из v рёбер) и  2 ( v ) — количество заходящих в v рёбер (тех, для которых эта вершина является концом).

1. Изображаем ребра . Нарисуем ориентированный граф состоящий из пяти вершин , любые две из которых соединены ориентированным ребром (дугой). Изобразите пять вершин, переименуйте их, изобразите недостающие ребра. Для этого на панели инструментов выбираем рисовать Прямая по двум точкам . Наводим мышку на стрелочку внизу, она становится красной, нажимаем на нее правой кнопкой мыши, открывается скрытая вкладка, выбираем в ней Вектор по двум точкам . В области геометрии выбираем точку v 1 (начало ребра), для этого наводим на нее курсор и нажимаем правую кнопку мыши, таким же образом выбираем точку v 2 (конец ребра). Таким же образом, изображаем все необходимые дуги.

Подпишем ребра графа.

Задание 1 . Полученный орграф преобразуйте в орграфы с шестью вершинами и четырьмя вершинами. Сохранить граф с шестью вершинами.

Задание 2. 1. Составить множество Е i и нарисовать диаграмму орграфа i ( V , E i ), где V = , а E i  бинарное отношение, заданное на множестве V :

Подсказка . Изобразите все пять вершин, и подпишите их. В результате получим:

а) Выбираем две вершины, например 5 и 10, они будут соединены ребром, так 5+10=15, вершины 5 и 0, не соединены ребром, так как 5+0≠15.

Рассуждая, таким образом, построим граф 1 ( V , E 1 ):

Двойные стрелочки указывают на то, что изображено два ребра в одну и другую сторону. Самостоятельно постройте остальные графы. Перенесите задание и диаграммы графов в тетрадь.

2. Изобразите полные ориентированные графы с шестью, пятью и четырьмя вершинами. Сколько ребер у полного орграфа с 4 (5 и 6) вершинами? Сколько ребер у полного орграфа с n вершинами?

Подсказка . Это можно сделать, например, так.

Кратные ребра изображаются при помощи дополнительной точки, отрезка и вектора (дополнительную точку нужно скрыть). В полном ориентированном графе каждая вершина соединена со всеми остальными, не забудьте, что ребра считаются разными, если у них различная ориентация. Изображенный граф является регулярным орграфом степени 3.

3. Изобразите регулярный орграф степени 2 и 3 с шестью вершинами. Сколько ребер у регулярного орграфа степени 2 (степени 3) в случае n вершин? Сколько ребер у регулярного орграфа степени k в случае n вершин?

Подсказка . Для вершин ориентированного графа определяются две локальные степени:  1 ( v ) — число рёбер с началом в вершине v (количество выходящих из v рёбер) и  2 ( v ) — количество заходящих в v рёбер (тех, для которых эта вершина является концом).

Ориентированный граф называется однородным степени k , если для каждой его вершины  1 ( v )=  2 ( v )= k .

Задание 3. 1. Постройте диаграммы орграфа с семью вершинами и 13 ребрами.

Подсказка . Вершины орграфа лучше изображать окружностями одинакового диаметра (для этого необходимо изобразить 7 точек, и на панели инструментов в вкладке Окружность по центру и точке , выберите Окружность по центру и радиусу радиус можно выбрать равным 0.3(десятичная дробь задается через точку)), а ребра векторами. Например, можно изобразить этот граф так.

Подпишите вершины графа.

Сохраните файл с этим графом. В меню выбрать Файл-сохранить как… имя файла Орграф .

2. Орграф с семью вершинами и 13 ребрами преобразуйте в мультиорграф, для этого изобразите несколько кратных ребер. Подпишите ребра.

Сохраните файл с этим графом. В меню выбрать Файл-сохранить как… имя файла Мультиорграф .

3. Орграф с семью вершинами и 13 ребрами преобразуйте в ориентированный псевдограф, для этого изобразите несколько петель (ребер у которых совпадает начало и конец).

Сохраните файл с этим графом. В меню выбрать Файл-сохранить как… имя файла Псевдоорграф1 .

4. Мультиорграф с семью вершинами и 16 ребрами преобразуйте в ориентированный псевдограф, для этого изобразите несколько петель.

Сохраните файл с этим графом. В меню выбрать Файл-сохранить как… имя файла Псевдоорграф2 .

5. Для орграфа, мультиорграфа и 2-х ориентированных псевдографов из задание 3 определите две степени всех вершин и сумму для каждой степени (выпишите в тетрадь диаграммы орграфа, мультиорграфа и 2-х ориентированных псевдографов, две степени каждой вершины и сумму для каждой степени для каждого графа).

Подсказка . Петля даёт вклад 1 в обе эти степени. Очевидно, что общее количество всех выходящих рёбер равно общему количеству всех входящих рёбер и равно количеству рёбер этого графа: m ==.

9. Существуют ли орграф со следующими степенями  1 вершин:

Видео:Графы.Вступление. Виды графов,степень вершин, ориентированный графСкачать

1. Графы. Основные понятия и определения. Матрицы смежностей вершин графов. Матрицы инциденций графов и орграфов. Степени вершин и полустепени исхода и захода. Основные типы графов.

Видео:Графы | Степень вершины | Лемма о рукопожатиях | Компоненты связностиСкачать

Основные понятия и определения.

Пара (V(G), E(G)) называется простым графом, если V(G) – непустое конечное множество элементов, называемых вершинами (или узлами, или точками), а E(G) – конечное множество неупорядоченных пар различных элементов из V(G), называемых ребрами (или линиями). В простом графе данную пару вершин может соединять не более чем одно ребро.

Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v1, v2, если оно соединяет эти вершины и наоборот, каждая из вершин v1, v2 инцидентна ребру е.

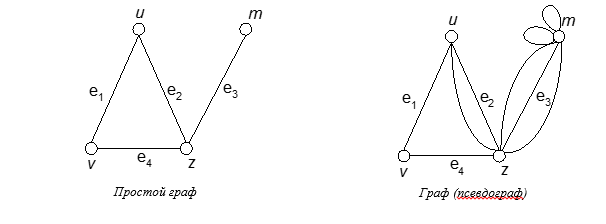
Часто бывает удобно снять ограничение, состоящее в том, что ребро должно соединять две различные вершины, и допустить существование петель.
Получающийся при этом объект, в котором могут быть и кратные ребра и петли называется графом (псевдографом).

Псевдограф без петель называется мультиграфом.

Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа.

Кратностью ребер называют количество одинаковых пар.

пример

Мультиграф в котором ни одна пара не встречается более одного раза называется графом.

Две вершины называются смежными, если существует ребро, концами которого они являются. Два ребра называются смежными, если они имеют общую вершину.

Смежные вершины – вершины, инцидентные одной дуге.
Смежные дуги – это дуги инцидентные одной вершине.

Видео:Графы, вершины, ребра, инцидентность, смежностьСкачать

Степени вершин и полустепени исхода и захода.

Степенью вершины v графа G называется число ребер графа, которым инцидентна эта вершина.

Вершина, локальная степень которой равна 0, называется изолированной; степень которой равна 1 – висячей.

Полустепенью исхода (захода) вершины v орграфа D называется число дуг орграфа D, исходящих из вершины v (заходящих в вершину v).

Количество вершин и ребер в графе G обозначим соответственно через n(G) и m(G), а количество вершин и дуг в орграфе D – через n(D) и m(D).

Для любого псевдографа G выполняется равенство

(Cумма степеней всех вершин = удвоенное количество ребер в графе)

Для любого ориентированного псевдографа D выполняется равенство

(Cумма полустепеней исхода и захода всех вершин = количество ребер в графе)

Два графа G1 и G2 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в G1, равно число ребер, соединяющих соответствующие вершины в G2.

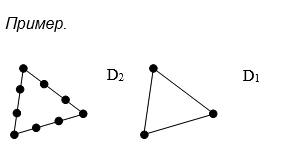
Операция подразбиения (измельчения) дуги (u, v) в орграфе D = (V, E) состоит в удалении из Е дуги (u, v), добавлении к V новой вершины w и добавлении к Е | двух дуг (u, w), (w, v). Аналогично определяется операция подразбиения ребра в графах.

Орграф D1 называется подразбиением орграфа D2, если орграф D1 можно получить из D2 путем последовательного применения операции подразбиения дуг. Аналогично определяется подразбиение графа.

Орграфы D1, D2 называются гомеоморфными, если существуют их подразбиения, являющиеся изоморфными.

Видео:Степени вершина графаСкачать

Матрицы смежностей и инциденций вершин графов и орграфов.

Матрицей смежности орграфа D называется квадратная матрица A(D)=[aij] порядка n, у которой

Матрицей инцидентности орграфа D называется (nxm) –матрица B(D)=[bij], у которой

Матрицей смежности графа G называется квадратная матрица A(G)=[aij] порядка n, у которой

Матрицей инцидентности графа G называется (nxm) –матрица B(G)=[bij], у которой

Основные свойства матриц смежности:

Матрица смежностей вершин неориентированного графа A (G) является квадратной и симметричной относительно главной диагонали.
Элементами матрицы A (G) являются целые положительные числа и число ноль.
Сумма элементов матрицы A (G) по i-й строке (или по i-му столбцу) равна степени соответствующей вершины δ ( xi ).

Из определения следует, что сумма элементов i-й строки матрицы A (G)орграфа равна полустепени исхода δ+ ( xi ), а по i-му столбцу – полустепени захода δ¯ ( xi ).

Свойства матрицы инцидентности неориентированного графа:

Сумма элементов матрицы на i-й строке равна δ ( xi ).
Сумма элементов матрицы по i-му столбцу равна 2.

Матрица инцидентности орграфа G обладает следующими свойствами:

Сумма строк матрицы B(G) является нулевой строкой.
Любая строка матрицы B(G) является линейной комбинацией остальных строк.
Ранг матрицы B(G) равен p-1.

Видео:Графы. Степень вершины графа. Подготовка к олимпиаде по математикеСкачать

Основные типы графов.

Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Вполне несвязный граф обозначают Nn.

Простой граф, в котором любые две вершины смежны, называется полным. Полный граф обозначают Кn.

Граф, у которого все вершины имеют одну и ту же локальную степень n, называется регулярным (или однородным) степени n. Регулярные графы степени 3 называются кубическими (или трехвалентными). Среди регулярных графов особенно интересны так называемые платоновы графы – графы, образованные вершинами и ребрами пяти правильных многогранников — Платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.

Допустим, что множество вершин графа G можно разбить на два непересекающихся подмножества V1 и V2 так, что каждое ребро в G соединяет какую-нибудь вершину из V1 с какой-нибудь вершиной из V2, тогда данный граф называется двудольным.

Если в двудольном графе каждая вершина из V1 соединена с каждой вершиной из V2, то граф называется полным двудольным.

Граф называется связным, если его нельзя представить в виде объединения двух графов, и несвязным в противном случае.

Очевидно, что всякий несвязный граф можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой связности графа.

Определение. Связный регулярный граф степени 2 называется циклическим графом.

Смешанный граф — Граф, содержащий как ориентированные, так и неориентированные рёбра