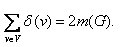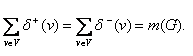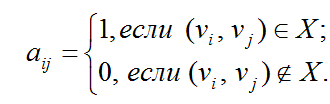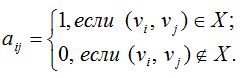Вектор степеней вершин графа (2 видео) | Курс школьной геометрии

1. Графы. Основные понятия и определения. Матрицы смежностей вершин графов. Матрицы инциденций графов и орграфов. Степени вершин и полустепени исхода и захода. Основные типы графов.

Содержание

Основные понятия и определения.
Степени вершин и полустепени исхода и захода.
Матрицы смежностей и инциденций вершин графов и орграфов.
Основные типы графов.
3.02.1. Основные числовые характеристики и матрицы графа. Степени вершин графа
Степени вершин графа
🔍 Видео

Видео:Графы, вершины, ребра, инцидентность, смежностьСкачать

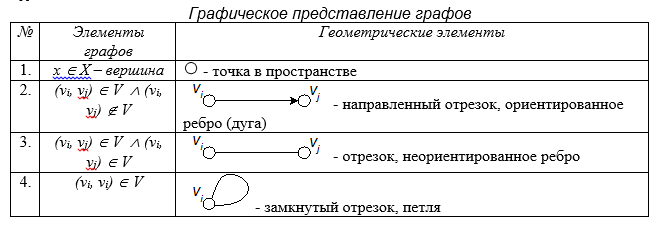
Основные понятия и определения.

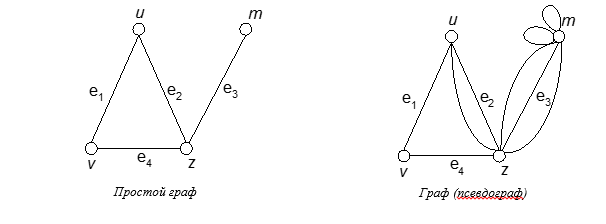
Пара (V(G), E(G)) называется простым графом, если V(G) – непустое конечное множество элементов, называемых вершинами (или узлами, или точками), а E(G) – конечное множество неупорядоченных пар различных элементов из V(G), называемых ребрами (или линиями). В простом графе данную пару вершин может соединять не более чем одно ребро.

Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v1, v2, если оно соединяет эти вершины и наоборот, каждая из вершин v1, v2 инцидентна ребру е.

Часто бывает удобно снять ограничение, состоящее в том, что ребро должно соединять две различные вершины, и допустить существование петель.
Получающийся при этом объект, в котором могут быть и кратные ребра и петли называется графом (псевдографом).

Псевдограф без петель называется мультиграфом.

Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа.

Кратностью ребер называют количество одинаковых пар.

пример

Мультиграф в котором ни одна пара не встречается более одного раза называется графом.

Две вершины называются смежными, если существует ребро, концами которого они являются. Два ребра называются смежными, если они имеют общую вершину.

Смежные вершины – вершины, инцидентные одной дуге.
Смежные дуги – это дуги инцидентные одной вершине.

Видео:Графы | Степень вершины | Лемма о рукопожатиях | Компоненты связностиСкачать

Степени вершин и полустепени исхода и захода.

Степенью вершины v графа G называется число ребер графа, которым инцидентна эта вершина.

Вершина, локальная степень которой равна 0, называется изолированной; степень которой равна 1 – висячей.

Полустепенью исхода (захода) вершины v орграфа D называется число дуг орграфа D, исходящих из вершины v (заходящих в вершину v).

Количество вершин и ребер в графе G обозначим соответственно через n(G) и m(G), а количество вершин и дуг в орграфе D – через n(D) и m(D).

Для любого псевдографа G выполняется равенство

(Cумма степеней всех вершин = удвоенное количество ребер в графе)

Для любого ориентированного псевдографа D выполняется равенство

(Cумма полустепеней исхода и захода всех вершин = количество ребер в графе)

Два графа G1 и G2 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в G1, равно число ребер, соединяющих соответствующие вершины в G2.

Операция подразбиения (измельчения) дуги (u, v) в орграфе D = (V, E) состоит в удалении из Е дуги (u, v), добавлении к V новой вершины w и добавлении к Е | двух дуг (u, w), (w, v). Аналогично определяется операция подразбиения ребра в графах.

Орграф D1 называется подразбиением орграфа D2, если орграф D1 можно получить из D2 путем последовательного применения операции подразбиения дуг. Аналогично определяется подразбиение графа.

Орграфы D1, D2 называются гомеоморфными, если существуют их подразбиения, являющиеся изоморфными.

Видео:Степени вершина графаСкачать

Матрицы смежностей и инциденций вершин графов и орграфов.

Матрицей смежности орграфа D называется квадратная матрица A(D)=[aij] порядка n, у которой

Матрицей инцидентности орграфа D называется (nxm) –матрица B(D)=[bij], у которой

Матрицей смежности графа G называется квадратная матрица A(G)=[aij] порядка n, у которой

Матрицей инцидентности графа G называется (nxm) –матрица B(G)=[bij], у которой

Основные свойства матриц смежности:

Матрица смежностей вершин неориентированного графа A (G) является квадратной и симметричной относительно главной диагонали.
Элементами матрицы A (G) являются целые положительные числа и число ноль.
Сумма элементов матрицы A (G) по i-й строке (или по i-му столбцу) равна степени соответствующей вершины δ ( xi ).

Из определения следует, что сумма элементов i-й строки матрицы A (G)орграфа равна полустепени исхода δ+ ( xi ), а по i-му столбцу – полустепени захода δ¯ ( xi ).

Свойства матрицы инцидентности неориентированного графа:

Сумма элементов матрицы на i-й строке равна δ ( xi ).
Сумма элементов матрицы по i-му столбцу равна 2.

Матрица инцидентности орграфа G обладает следующими свойствами:

Сумма строк матрицы B(G) является нулевой строкой.
Любая строка матрицы B(G) является линейной комбинацией остальных строк.
Ранг матрицы B(G) равен p-1.

Видео:24 Сумма степеней вершин графа вдвое больше количества его рёберСкачать

Основные типы графов.

Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Вполне несвязный граф обозначают Nn.

Простой граф, в котором любые две вершины смежны, называется полным. Полный граф обозначают Кn.

Граф, у которого все вершины имеют одну и ту же локальную степень n, называется регулярным (или однородным) степени n. Регулярные графы степени 3 называются кубическими (или трехвалентными). Среди регулярных графов особенно интересны так называемые платоновы графы – графы, образованные вершинами и ребрами пяти правильных многогранников — Платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.

Допустим, что множество вершин графа G можно разбить на два непересекающихся подмножества V1 и V2 так, что каждое ребро в G соединяет какую-нибудь вершину из V1 с какой-нибудь вершиной из V2, тогда данный граф называется двудольным.

Если в двудольном графе каждая вершина из V1 соединена с каждой вершиной из V2, то граф называется полным двудольным.

Граф называется связным, если его нельзя представить в виде объединения двух графов, и несвязным в противном случае.

Очевидно, что всякий несвязный граф можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой связности графа.

Определение. Связный регулярный граф степени 2 называется циклическим графом.

Смешанный граф — Граф, содержащий как ориентированные, так и неориентированные рёбра

Видео:Графы.Вступление. Виды графов,степень вершин, ориентированный графСкачать

3.02.1. Основные числовые характеристики и матрицы графа. Степени вершин графа

Степенью вершины V графа G называется число инцидентных ей рёбер, т. е. число рёбер, выходящих из данной вершины. (В случае псевдографов каждая петля добавляет 2 в степень вершины). Обозначается степень вершины V графа G: degGv или просто deg V, если ясно, о каком графе G идет речь.

Вершина степени 0 называется Изолированной. Вершина степени 1 называется Концевой (или Висячей). Ребро, инцидентное концевой вершине также

Называется Концевым.

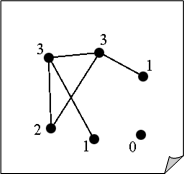
Вершина V Графа G, смежная со всеми другими вершинами G, называется Доминирующей. Её степень degGv очевидно равна |G| —1.

Граф G называется Регулярным (или, по-другому, Однородным), если степени всех его вершин равны. Эта общая степень всех вершин регулярного графа G называется степенью регулярного графа G и обозначается deg G.

Последовательность степеней вершин графа G, записанная в каком либо порядке называется степенной последовательностью графа G. Например, граф на рисунке справа имеет степенную последовательность (3, 3, 1, 0, 1, 2).

Понятно, что изоморфные графы имеют одинаковые (с точностью до порядка следования элементов) степенные последовательности. Однако, из этого совпадения степенных последовательностей двух графов ещё не следует их изоморфность. На следующих двух рисунках изображены два неизоморфных регулярных графа степени 2.

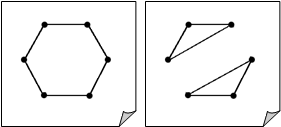
Таким образом, степенная последовательность не определяет граф полностью и не может

служить способом его задания.

Степенная последовательность не может быть произвольным набором чисел, а обладает определёнными свойствами.

Лемма 1 («о рукопожатиях»). Сумма степеней всех вершин графа G есть число чётное, ровно в два раза большее числа рёбер графа G, т. е.

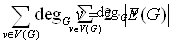Доказательство: Действительно, подсчитаем количество рёбер графа G, просматривая поочередно все вершины графа G и считая рёбра выходящие из этих вершин. Так как из каждой вершины V выходит degGV рёбер, то мы получим сумму:

Но при этом каждое ребро будет учтено 2 раза: один раз, когда рассматривался один его конец, другой раз, когда — второй. Таким образом, лемма верна.

Из леммы 1 вытекает

Следствие. В любом графе число вершин нечётной степени является чётным.

Доказательство. В самом деле, иначе, если бы сумма целых чисел содержала нечётное число нечетных слагаемых, то она, очевидно, была бы нечётной, что противоречит лемме о рукопожатиях.

В ориентированных графах для каждой вершины V дополнительно рассматривается также полустепень исхода и полустепень захода. Полустепенью исхода вершины V называется число дуг графа G, для которых V Является началом, а Полустепенью захода – число дуг, для которых V является концом. Обозначаются полустепени захода и исхода графа G соответственно deg-V и deg+V. При этом полная степень degV = deg-V+ deg+V. Поскольку каждая дуга имеет ровно одно начало и один конец, то справедлива

Видео:4.8 Степени вершин графовСкачать

Степени вершин графа

Степенью вершины графа называется количество инцидентных ей ребер (для петли степень подсчитывается дважды). Через а(х) будем обозначать степень вершины х. Для графа на рис. 4 вершины имеют следующие степени:

Ясно, что степень любой вершины конечного графа есть целое неотрицательное число. Вообще, определенное нами понятие степени имеет смысл лишь для вершин, инцидентных конечному числу ребер, при этом множество вершин и множество ребер графа могут быть бесконечными. Так, на рис. 6 представлен бесконечный граф, все вершины которого имеют степень 4 (кроме первой вершины, имеющей степень 2). Этот граф моделирует так называемые размножения».

Вершина графа степени 0 называется изолированной. Если степень вершины равна 1, то она называется концевой или висячей вершиной. Вершина, степень которой больше или равна 2, называется промежуточной или проходной. Так, на рис. 4 вершина D — изолированная, вершина С — висячая, а остальные вершины — проходные.

Вершины графа называются четными или нечетными в зависимости от четности их степеней. Так, в графе на рис. 6 все вершины — четные. Граф на рис. 4 имеет две нечетные вершины (С и Н),а остальные вершины этого графа — четные.

Теорема 1. В любом конечном графе G(V, Е) количество нечетных вершин — четно.

Действительно, каждое ребро добавляет по единице к степеням своих граничных вершин, а каждая петля добавляет двойку к степени своей вершины. Поэтому сумма степеней всех вершин равна удвоенному числу ребер графа:

Здесь через Е обозначено число элементов во множестве

Е, т.е. количество ребер графа G. Формула (1.4.1) показывает, что сумма степеней всех вершин графа есть четное число. Поэтому в эту сумму может входить лишь четное количество нечетных слагаемых, т.е. количество нечетных вершин графа G есть четное число.

Следствие. Сумма степеней всех вершин конечного графа равна удвоенному числу его ребер.

Задачи и упражнения

1. Докажите, что число перекрестков любого города, в которых встречается нечетное число улиц — четно.
2. У марсиан бывает произвольное число рук. Однажды все марсиане взялись за руки так, что свободных рук не осталось. Докажите, что количество марсиан с нечетным числом рук четно.
3. Докажите, что число зрителей, пришедших на стадион смотреть футбольный матч и имеющих нечетное число знакомых (среди того же множества зрителей) четно.
4. Докажите, что число людей, когда-либо живших на Земле и сделавших нечетное число рукопожатий, четно.
5. В классе 30 человек. Может ли быть так, что 9 из них имеют по 5 друзей каждый, 11 — по 4 друга и 10 — по 3 друга?
6. В офисе 15 телефонов. Можно ли их соединить между собой проводами так, чтобы каждый был соединен с 3 другими?
7. Можно ли нарисовать на плоскости 11 отрезков так, чтобы каждый пересекался ровно с тремя другими?
8. В государстве 100 городов, и из каждого из них выходит по 4 дороги. Сколько всего дорог в государстве?
9. Может ли в государстве, в котором из каждого города выходит ровно по три дороги, быть 100 дорог?
10. На радиостанции каждый радиоузел соединен ровно с 15 другими. Может ли быть число проводов на радиостанции равно 200?

Во всех задачах нужно смоделировать условия при помощи графов. Задачи 1-7 решаются при помощи теоремы 1, а при решении задач 8-10 нужно использовать следствие из этой теоремы.

Доказательство утверждений в задачах 1—4 дословно повторяет доказательство теоремы 1.

В задачах 5-7 ответ отрицательный, так как ситуации, соответствующие условиям каждой из этих задач, противоречат теореме 1.

7. Нужно рассмотреть граф, вершины которого соответствуют отрезкам, а ребра соединяют вершины, которым соответствуют пересекающиеся отрезки.
8. Рассмотрим граф G(V, Е), у которого множество вершин V состоит из 100 городов, а множество ребер Е состоит из всех дорог государства. По условию задачи каждая вершина этого графа имеет степень 4. Применяя формулу (1.4.1), получим, что 4100 = 2-|?|.

Следовательно, количество дорог |?| равно 200.

9. Моделируя условие задачи так же, как в задаче 8, и применяя следствие из теоремы 1, получим: 3-|f| = 2• 100. Так как количество вершин |f| должно

быть натуральным числом, то ответ на вопрос задачи — отрицательный.

10. Ответ к задаче — отрицательный. Ее решение аналогично решению задачи 9.