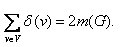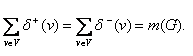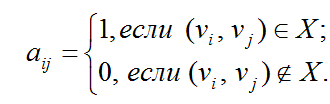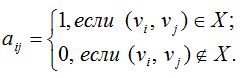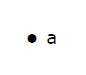- Основные понятия и определения.
- Степени вершин и полустепени исхода и захода.
- Матрицы смежностей и инциденций вершин графов и орграфов.
- Основные типы графов.
- 3.02.1. Основные числовые характеристики и матрицы графа. Степени вершин графа
- Теория графов — основы
- точка
- пример
- Линия
- пример
- пример
- пример
- график
- Пример 1
- Пример 2
- петля
- Пример 1
- Пример 2
- Степень вершины
- Степень вершины в неориентированном графе
- Пример 1
- Пример 2
- Степень вершины в ориентированном графе
- Степень графа
- Степень графа
- Пример 1
- Пример 2
- Кулон Вертекс
- пример
- Изолированная вершина
- пример
- смежность
- Пример 1
- Пример 2
- Параллельные края
- Мульти График
- Пример 1
- Пример 2
- Степень последовательности графика
- Пример 1
- Пример 2
- 🌟 Видео
Видео:Графы, вершины, ребра, инцидентность, смежностьСкачать

Основные понятия и определения.
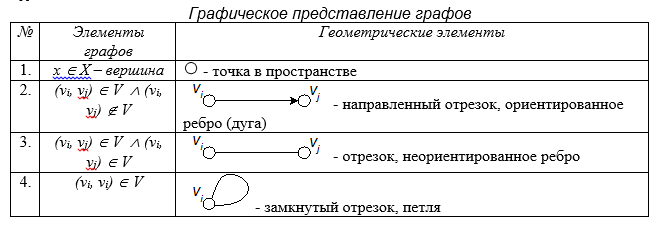
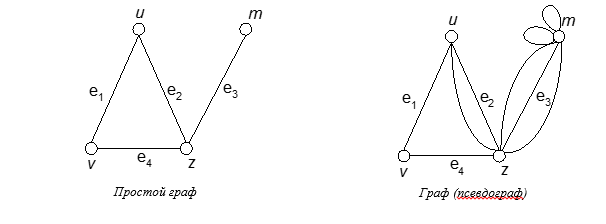
Пара (V(G), E(G)) называется простым графом, если V(G) – непустое конечное множество элементов, называемых вершинами (или узлами, или точками), а E(G) – конечное множество неупорядоченных пар различных элементов из V(G), называемых ребрами (или линиями). В простом графе данную пару вершин может соединять не более чем одно ребро.
Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v1, v2, если оно соединяет эти вершины и наоборот, каждая из вершин v1, v2 инцидентна ребру е.
Часто бывает удобно снять ограничение, состоящее в том, что ребро должно соединять две различные вершины, и допустить существование петель.
Получающийся при этом объект, в котором могут быть и кратные ребра и петли называется графом (псевдографом).
Псевдограф без петель называется мультиграфом.
Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа.
Кратностью ребер называют количество одинаковых пар.
пример
Мультиграф в котором ни одна пара не встречается более одного раза называется графом.
Две вершины называются смежными, если существует ребро, концами которого они являются. Два ребра называются смежными, если они имеют общую вершину.
Смежные вершины – вершины, инцидентные одной дуге.
Смежные дуги – это дуги инцидентные одной вершине.
Видео:4.8 Степени вершин графовСкачать

Степени вершин и полустепени исхода и захода.
Степенью вершины v графа G называется число ребер графа, которым инцидентна эта вершина.
Вершина, локальная степень которой равна 0, называется изолированной; степень которой равна 1 – висячей.
Полустепенью исхода (захода) вершины v орграфа D называется число дуг орграфа D, исходящих из вершины v (заходящих в вершину v).
Количество вершин и ребер в графе G обозначим соответственно через n(G) и m(G), а количество вершин и дуг в орграфе D – через n(D) и m(D).
Для любого псевдографа G выполняется равенство
(Cумма степеней всех вершин = удвоенное количество ребер в графе)
Для любого ориентированного псевдографа D выполняется равенство
(Cумма полустепеней исхода и захода всех вершин = количество ребер в графе)
Два графа G1 и G2 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в G1, равно число ребер, соединяющих соответствующие вершины в G2.
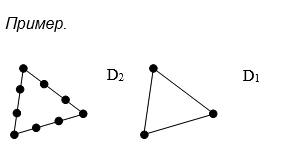
Операция подразбиения (измельчения) дуги (u, v) в орграфе D = (V, E) состоит в удалении из Е дуги (u, v), добавлении к V новой вершины w и добавлении к Е | двух дуг (u, w), (w, v). Аналогично определяется операция подразбиения ребра в графах.
Орграф D1 называется подразбиением орграфа D2, если орграф D1 можно получить из D2 путем последовательного применения операции подразбиения дуг. Аналогично определяется подразбиение графа.
Орграфы D1, D2 называются гомеоморфными, если существуют их подразбиения, являющиеся изоморфными.
Видео:Графы | Степень вершины | Лемма о рукопожатиях | Компоненты связностиСкачать

Матрицы смежностей и инциденций вершин графов и орграфов.
Матрицей смежности орграфа D называется квадратная матрица A(D)=[aij] порядка n, у которой
Матрицей инцидентности орграфа D называется (nxm) –матрица B(D)=[bij], у которой
Матрицей смежности графа G называется квадратная матрица A(G)=[aij] порядка n, у которой
Матрицей инцидентности графа G называется (nxm) –матрица B(G)=[bij], у которой
Основные свойства матриц смежности:
- Матрица смежностей вершин неориентированного графа A (G) является квадратной и симметричной относительно главной диагонали.
- Элементами матрицы A (G) являются целые положительные числа и число ноль.
- Сумма элементов матрицы A (G) по i-й строке (или по i-му столбцу) равна степени соответствующей вершины δ ( xi ).
Из определения следует, что сумма элементов i-й строки матрицы A (G)орграфа равна полустепени исхода δ+ ( xi ), а по i-му столбцу – полустепени захода δ¯ ( xi ).
Свойства матрицы инцидентности неориентированного графа:
- Сумма элементов матрицы на i-й строке равна δ ( xi ).
- Сумма элементов матрицы по i-му столбцу равна 2.
Матрица инцидентности орграфа G обладает следующими свойствами:
- Сумма строк матрицы B(G) является нулевой строкой.
- Любая строка матрицы B(G) является линейной комбинацией остальных строк.
- Ранг матрицы B(G) равен p-1.
Видео:Степени вершина графаСкачать

Основные типы графов.
Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Вполне несвязный граф обозначают Nn.
Простой граф, в котором любые две вершины смежны, называется полным. Полный граф обозначают Кn.
Граф, у которого все вершины имеют одну и ту же локальную степень n, называется регулярным (или однородным) степени n. Регулярные графы степени 3 называются кубическими (или трехвалентными). Среди регулярных графов особенно интересны так называемые платоновы графы – графы, образованные вершинами и ребрами пяти правильных многогранников — Платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.
Допустим, что множество вершин графа G можно разбить на два непересекающихся подмножества V1 и V2 так, что каждое ребро в G соединяет какую-нибудь вершину из V1 с какой-нибудь вершиной из V2, тогда данный граф называется двудольным.
Если в двудольном графе каждая вершина из V1 соединена с каждой вершиной из V2, то граф называется полным двудольным.
Граф называется связным, если его нельзя представить в виде объединения двух графов, и несвязным в противном случае.
Очевидно, что всякий несвязный граф можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой связности графа.
Определение. Связный регулярный граф степени 2 называется циклическим графом.
Смешанный граф — Граф, содержащий как ориентированные, так и неориентированные рёбра
Видео:Графы.Вступление. Виды графов,степень вершин, ориентированный графСкачать

3.02.1. Основные числовые характеристики и матрицы графа. Степени вершин графа
Степенью вершины V графа G называется число инцидентных ей рёбер, т. е. число рёбер, выходящих из данной вершины. (В случае псевдографов каждая петля добавляет 2 в степень вершины). Обозначается степень вершины V графа G: degGv или просто deg V, если ясно, о каком графе G идет речь.
Вершина степени 0 называется Изолированной. Вершина степени 1 называется Концевой (или Висячей). Ребро, инцидентное концевой вершине также
Вершина V Графа G, смежная со всеми другими вершинами G, называется Доминирующей. Её степень degGv очевидно равна |G| —1.
Граф G называется Регулярным (или, по-другому, Однородным), если степени всех его вершин равны. Эта общая степень всех вершин регулярного графа G называется степенью регулярного графа G и обозначается deg G.
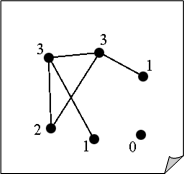
Последовательность степеней вершин графа G, записанная в каком либо порядке называется степенной последовательностью графа G. Например, граф на рисунке справа имеет степенную последовательность (3, 3, 1, 0, 1, 2).
Таким образом, степенная последовательность не определяет граф полностью и не может
служить способом его задания.
Степенная последовательность не может быть произвольным набором чисел, а обладает определёнными свойствами.
Лемма 1 («о рукопожатиях»). Сумма степеней всех вершин графа G есть число чётное, ровно в два раза большее числа рёбер графа G, т. е.
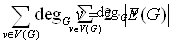 |
Доказательство: Действительно, подсчитаем количество рёбер графа G, просматривая поочередно все вершины графа G и считая рёбра выходящие из этих вершин. Так как из каждой вершины V выходит degGV рёбер, то мы получим сумму:
Но при этом каждое ребро будет учтено 2 раза: один раз, когда рассматривался один его конец, другой раз, когда — второй. Таким образом, лемма верна.
Из леммы 1 вытекает
Следствие. В любом графе число вершин нечётной степени является чётным.
Доказательство. В самом деле, иначе, если бы сумма целых чисел содержала нечётное число нечетных слагаемых, то она, очевидно, была бы нечётной, что противоречит лемме о рукопожатиях.
В ориентированных графах для каждой вершины V дополнительно рассматривается также полустепень исхода и полустепень захода. Полустепенью исхода вершины V называется число дуг графа G, для которых V Является началом, а Полустепенью захода – число дуг, для которых V является концом. Обозначаются полустепени захода и исхода графа G соответственно deg-V и deg+V. При этом полная степень degV = deg-V+ deg+V. Поскольку каждая дуга имеет ровно одно начало и один конец, то справедлива
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Теория графов — основы
График — это диаграмма точек и линий, соединенных с точками. У него есть по крайней мере одна линия, соединяющая набор из двух вершин без вершин, соединяющих себя. Понятие графов в теории графов опирается на некоторые основные термины, такие как точка, линия, вершина, ребро, степень вершин, свойства графов и т. Д. Здесь, в этой главе, мы рассмотрим эти основы теории графов.
Видео:Диаметр графа. Радиус. Эксцентриситет. ЦентрСкачать

точка
Точка — это конкретная позиция в одномерном, двухмерном или трехмерном пространстве. Для лучшего понимания точку можно обозначить алфавитом. Его можно обозначить точкой.
пример
Здесь точка — это точка с именем «а».
Видео:5-часовой веб по ГРАФАМСкачать

Линия
Линия — это связь между двумя точками. Это может быть представлено сплошной линией.
пример
Здесь «а» и «б» являются точками. Связь между этими двумя точками называется линией.
Вершина — это точка, где встречаются несколько линий. Это также называется узлом . Подобно точкам, вершина также обозначается алфавитом.
пример
Здесь вершина названа с алфавитом «а».
Ребро — это математический термин для линии, соединяющей две вершины. Многие ребра могут быть сформированы из одной вершины. Без вершины ребро не может быть сформировано. Для ребра должна быть начальная и конечная вершина.
пример
Здесь «a» и «b» — две вершины, и связь между ними называется ребром.
Видео:Математика| СтепениСкачать

график
Граф ‘G’ определяется как G = (V, E), где V — множество всех вершин, а E — множество всех ребер графа.
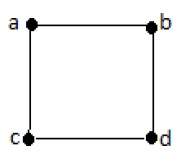
Пример 1
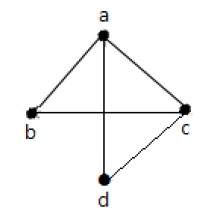
В приведенном выше примере ab, ac, cd и bd являются ребрами графа. Аналогично, a, b, c и d являются вершинами графа.
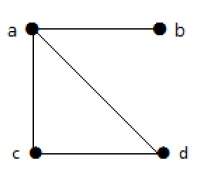
Пример 2
В этом графе есть четыре вершины a, b, c и d и четыре ребра ab, ac, ad и cd.
Видео:Графы. Степень вершины графа. Подготовка к олимпиаде по математикеСкачать

петля
В графе, если ребро нарисовано от вершины к себе, это называется циклом.
Пример 1
На приведенном выше графике V — вершина, для которой у нее есть ребро (V, V), образующее петлю.
Пример 2
В этом графе есть две петли, которые сформированы в вершине a, и вершине b.
Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Степень вершины
Это число вершин, смежных с вершиной V.
Обозначение — град (V).
В простом графе с n числом вершин степень любых вершин равна —
Вершина может образовывать ребро со всеми остальными вершинами, кроме самой себя. Таким образом, степень вершины будет равна числу вершин в графе минус 1 . Это 1 для собственной вершины, поскольку она не может образовывать петлю сама по себе. Если в любой из вершин есть петля, то это не простой граф.
Степень вершины можно рассматривать по двум случаям графов —
- Ненаправленный граф
- Направленный граф
Видео:Способы задать граф. Матрица векторов смежностиСкачать

Степень вершины в неориентированном графе
Ненаправленный граф не имеет направленных ребер. Рассмотрим следующие примеры.
Пример 1
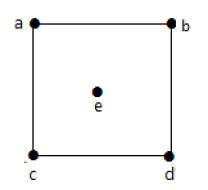
Посмотрите на следующий график —
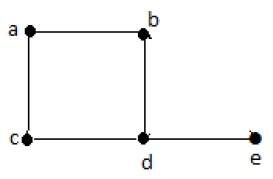
На приведенном выше неориентированном графике
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
Итак, «c» — это вершина с кулоном .
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
Так что «е» — изолированная вершина .
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
Итак, «c» — это вершина с кулоном .
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
Так что «е» — изолированная вершина .
Пример 2
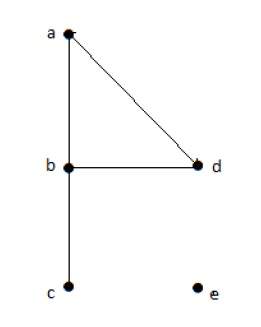
Посмотрите на следующий график —
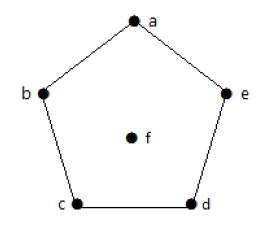
На приведенном выше графике
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 и deg (e) = 0.
Вершина «е» является изолированной вершиной. Граф не имеет никакой вершины.
Видео:Характеристики вершин. Основная теорема теории графовСкачать

Степень вершины в ориентированном графе
В ориентированном графе каждая вершина имеет степень и степень.
Степень графа
Степень вершины V — это количество ребер, входящих в вершину V.
Обозначение — град — (V).
Степень вершины V — это количество ребер, входящих в вершину V.
Обозначение — град — (V).
Степень графа
Отступ вершины V — это число ребер, выходящих из вершины V.
Обозначение — град + (V).
Отступ вершины V — это число ребер, выходящих из вершины V.
Обозначение — град + (V).
Рассмотрим следующие примеры.
Пример 1
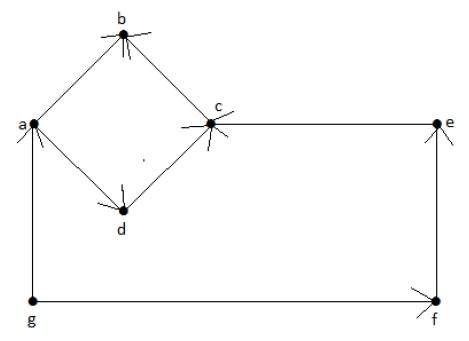
Посмотрите на следующий ориентированный граф. Вершина «а» имеет два ребра, «ad» и «ab», которые идут наружу. Следовательно, его степень равна 2. Аналогично, существует ребро «ga», идущее к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 2 | |
| б | 2 | 0 |
| с | 2 | 1 |
| d | 1 | 1 |
| е | 1 | 1 |
| е | 1 | 1 |
| г | 0 | 2 |
Пример 2
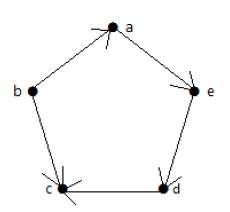
Посмотрите на следующий ориентированный граф. Вершина ‘a’ имеет ребро ‘ae’, идущее наружу от вершины ‘a’. Следовательно, его степень равна 1. Аналогично, у графа есть ребро «ba», приближающееся к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 1 | |
| б | 0 | 2 |
| с | 2 | 0 |
| d | 1 | 1 |
| е | 1 | 1 |
Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Кулон Вертекс
Используя степень вершины, мы получаем два специальных типа вершин. Вершина с первой степенью называется нерешенной вершиной.
пример
Здесь, в этом примере, вершина ‘a’ и вершина ‘b’ имеют соединенное ребро ‘ab’. Таким образом, что касается вершины «a», то к вершине «b» имеется только одно ребро, и аналогично по отношению к вершине «b» есть только одно ребро к вершине «a». Наконец, вершина ‘a’ и вершина ‘b’ имеют степень как единицу, которая также называется висячей вершиной.
Видео:Графы. Полный граф из 6 вершин, уникурсальностьСкачать

Изолированная вершина
Вершина с нулевой степенью называется изолированной вершиной.
пример
Здесь вершина «a» и вершина «b» не имеют связи между собой, а также с любыми другими вершинами. Таким образом, степень обеих вершин ‘a’ и ‘b’ равна нулю. Они также называются изолированными вершинами.
Видео:Занятие 2. Степени вершин и общие соседиСкачать

смежность
Вот нормы смежности —
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
Пример 1
На приведенном выше графике —
«a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
«a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
Пример 2
На приведенном выше графике —
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
Видео:39 Граф, степени вершин которого равны 6, на тореСкачать

Параллельные края
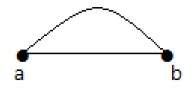
В графе, если пара вершин соединена более чем одним ребром, то эти ребра называются параллельными ребрами.
На приведенном выше графике «a» и «b» — это две вершины, которые соединены между собой двумя ребрами «ab» и «ab». Так это называется параллельным ребром.
Видео:24 Сумма степеней вершин графа вдвое больше количества его рёберСкачать

Мульти График
Граф, имеющий параллельные ребра, называется мультиграфом.
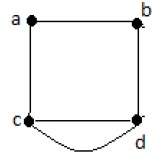
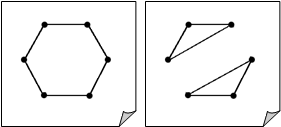
Пример 1
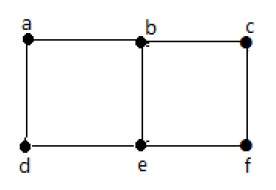
На приведенном выше графике есть пять ребер «ab», «ac», «cd», «cd» и «bd». Поскольку ‘c’ и ‘d’ имеют два параллельных ребра между ними, это мультиграф.
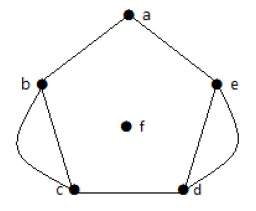
Пример 2
На приведенном выше графике вершины «b» и «c» имеют два ребра. Вершины ‘e’ и ‘d’ также имеют два ребра между ними. Следовательно, это мультиграф.
Видео:Скалярное произведение векторов. 9 класс.Скачать

Степень последовательности графика
Если степени всех вершин в графе расположены в порядке убывания или возрастания, то полученная последовательность называется последовательностью графа графа.
Пример 1
| темя | б | с | d | е | |
|---|---|---|---|---|---|
| Присоединенный к | До нашей эры | объявление | объявление | с, Ь, е | d |
| степень | 2 | 2 | 2 | 3 | 1 |
На приведенном выше графике для вершин последовательность степеней равна .
Пример 2
| темя | б | с | d | е | е | |
|---|---|---|---|---|---|---|
| Присоединенный к | быть | а, с | б, г | с, е | объявление | — |
| степень | 2 | 2 | 2 | 2 | 2 | 0 |
На приведенном выше графике для вершин последовательность степеней равна .
🌟 Видео
РАЗБОР ЗАДАЧИ - ТЕОРЕМА 1.Скачать