Mathcad поставляется с рядом функций для генерирования случайных чисел, имеющих разнообразные распределения вероятностей. Функциональные формы распределений, связанных с приведенными ниже функциями даны в подразделе “Распределения вероятности”.
Mathcad PLUS поставляется со всеми функциями, перечисленными в этом разделе. Если Вы не используете Mathcad PLUS, Вы будете иметь все генераторы случайных чисел, связанные со следующими законами распределения вероятностей: нормальным, хи-квадрат, t-распределением Стьюдента, F, биномиальным, Пуассона и равномерным.
| Е rbeta (m, s1, s2) | Возвращает вектор m случайных чисел, имеющих бэта-распределение. s1, s2 > 0 есть параметры формы. | |
| rbinom (m, n, p) | Возвращает вектор m случайных чисел, имеющих биномиальное распределение. 0  p p  1. n есть натуральное число. 1. n есть натуральное число. | |
| Е rcauchy (m, l, s) | Возвращает вектор m случайных чисел, имеющих распределение Коши. s > 0 есть параметр масштаба. l — параметр расположения. | |
| rchisq (m, d) | Возвращает вектор m случайных чисел, имеющих распределение хи-квадрат. d > 0 есть число степеней свободы. | |
| Е rexp (m, r) | Возвращает вектор m случайных чисел, имеющих экспоненциальное распределение. r > 0 — параметр распределения. | |
| rF (m, d1, d2) | Возвращает вектор m случайных чисел, имеющих F -распределение. d1, d2 > 0 есть числа степеней свободы. | |
| Е rgamma (m, s) | Возвращает вектор m случайных чисел, имеющих гамма- распределение, s > 0 есть параметр формы. | |
| Е rgeom (m, p) | Возвращает вектор m случайных чисел, имеющих геометрическое распределение. 0 Е rlnorm (m, m , s ) | Возвращает вектор m случайных чисел, имеющих логнормальное распределение, в котором m я вляется натуральным логарифмом среднего значения, а s > 0 есть натуральный логарифм среднеквадратичного отклонения. |
| Е rlogis (m, l, s) | Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а s > 0 есть параметр масштаба. | |
| Е rnbinom (m, n, p) | Возвращает вектор m случайных чисел, имеющих отрицательное биномиальное распределение. 0 m , s ) | Возвращает вектор m случайных чисел, имеющих нормальное распределение. s > 0. |
| rpois (m, l ) | Возвращает вектор m случайных чисел, имеющих распределение Пуассона. l > 0. | |
| rt (m, d) | Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента. d > 0. | |
| runif (m, a, b) | Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. a Е rweibull (m, s) | Возвращает вектор m случайных чисел, имеющих распределение Вейбулла, в котором s > 0 является параметром формы. |
Каждый раз, когда повторно вычисляется выражение, содержащее одну из этих функций, Mathcad генерирует новые случайные числа. Чтобы заставить Mathcad генерировать новые случайные числа, щёлкните мышью на выражении, содержащем функцию, и нажмите [F9]. Рисунок 3 показывает пример того, как использовать генератор случайных чисел Mathcad. Рисунок 4 показывает, как создать большой вектор случайных чисел, имеющих заданное распределение.
Каждая из этих функций в действительности создаёт последовательность псевдослучайных чисел, связанную с некоторым задаваемым стартовым значением. Каждое нажатие [F9] заставляет функцию выдать новое значение из этой последовательности. Одно и то же стартовое значение производит одинаковые последовательности чисел. Изменение стартового значения приводит к смене последовательности случайных чисел, выдаваемых функцией.
Чтобы изменить стартовое значение, выберите Генератор случайных чисел. из меню Математика и измените стартовое значение в диалоговом окне. Убедитесь, что введено целое число.
Чтобы перезапустить генератор случайных чисел Mathcad, не изменяя стартового значения, выберите Генератор случайных чисел. из меню Математика и нажмите “OK”, чтобы принять текущее значение. Затем щёлкните мышью на выражении с функцией, генерирующей случайное число, и нажмите [F9].
Рисунок 3: Равномерно распределенные случайные числа. Так как генератор случайных чисел производит каждый раз различные числа, маловероятно, что удастся в точности воспроизвести этот пример.
Рисунок 4: Вектор случайных чисел, распределенных по нормальному закону.
Так как генератор случайных чисел был сброшен, Mathcad будет производить те же самые случайные числа, которые производились бы после перезапуска Mathcad.
Если нужно несколько раз использовать одну и ту же последовательность случайных чисел, сбросьте генератор случайных чисел между вычислениями, как описано выше.
Чтобы получить новый набор случайных чисел, измените стартовое значение, как описано выше. Это заставит Mathcad генерировать набор случайных чисел, отличный от того, который создаётся после перезапуска Mathcad. Каждый раз при необходимости получить новую последовательность случайных чисел следует переустанавливать стартовое значение, как описано выше.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:Создание матриц в MathCAD 14 (18/34)Скачать
Вектор случайных чисел маткад
Глава 7. Математическая статистика
7.3 Генераторы случайных чисел
Для каждого закона распределения в MathCAD имеется функция-генератор случайных чисел, что позволяет выполнять моделирование методами Монте – Карло. Простейшая из них, функция rnd ( N ), возвращает одно случайное число, лежащее в интервале от 0 до N . Все другие функции-генераторы случайных чисел создают вектор чисел, распределенных по выбранному закону. Например, runif ( M , a , b ) создает вектор из М чисел, равномерно распределенных в интервале от a до b . Примеры работы генератора случайных чисел приведены на рис. 7.7 и 7.8.
создать одно случайное число, равномерно распределенное между 0 и х
(сотрите знак равенства и введите его вновь — число поменяется) rnd(x)





Опустите вниз оно из выражений V


среднее арифметическое
дисперсия
среднее квадратическое отклонение
медиана
Рис. 7.7 Работа генератора случайных чисел
Формирование массива случайных чисел
Для всех функций, кроме rnd 

поменяйте генератор
Для функции rnd 

Рис. 7.8 Работа генератора случайных чисел (продолжение)
Видео:Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

Формирование случайных сигналов (помех)
Формирование случайных сигналов (помех)
1. Формирование чисел с равномерным распределением
 |
Обычно в различных математических пакетах (языках программирования высокого уровня) имеются датчики случайных чисел, генерирующие последовательности чисел с равномерным распределением на интервале [a…b] (операторы random, rnd).
Наиболее часто для генерации чисел с равномерным законом распределения используется алгоритм вида
т. е. очередное случайное число α n+1 находится путем вычисления по модулю M произведения предыдущего рассчитанного значения α n на некоторое специально подобранное большое число K.
(Выполнить вычисление по модулю mod(x,m) – разделить x на m и в качестве результата взять остаток от деления).
Начальное число α 0 при первом обращении к генератору случайных чисел задается тем или иным образом программой, реализующей данный алгоритм. При следующих обращениях к генератору в качестве начального значения последовательности используется последний результат вычислений.
Значение M обычно задается наибольшим значением, равным M=231-1, при разрядности вычислений в 32 разряда, старший разряд – знаковый. 32 разряда используются для представления чисел с плавающей запятой с одинарной точностью. В результате упрощается операция вычисления по модулю: старшие разряды произведения, превышающие указанную разрядность, просто отбрасываются.
Генерируемые случайные числа являются целыми и распределены в интервале (0…M). Если генерируемые числа дополнительно разделить на M
то полученные числа будут распределены на интервале (0…1). Отметим, что равномерность распределения обеспечивается выбором числа K. Данное распределение является базовым для формирования случайных чисел с другими законами распределения.
Следует обратить внимание, что, если известно начальное значение α 0 и числа K и M, то вся последовательность генерируемых чисел легко просчитывается, поэтому такую последовательность логичнее называть псевдослучайной. Тем не менее, при неоднократных обращениях к генератору формируемые числа можно рассматривать как случайные.
В Mathcad случайное число генерируется при обращении к функции rnd(b), равномерно распределенное на интервале (0…b).
В окне Math – Options…- Bild In Variables – Seed value for random numbers задается начальное значение α 0, используемое при запуске пакета и первом обращении к функции rnd (по умолчанию Seed value = 1). Если после неоднократных обращений к rnd снова вызвать указанное выше окно и, сохраняя значение Seed value, закрыть окно по OK, то начальное значение α 0 для последующих обращений снова принимает значение, заданное в Seed value, что позволяет неоднократно воспроизводить одну и ту же последовательность случайных чисел.
2. Формирование величин с произвольным распределением
Наиболее общим методом формирования величин с произвольным законом распределения на основе равномерного является метод обратной функции. Метод основан на следующей теореме.
Если случайная величина x имеет плотность распределения вероятности p(x), то случайная величина

 |
будет распределена по равномерному закону на интервале (0…1) независимо от вида распределения p(x).
 |
Рис.1. Метод обратной функции.
Можно рассмотреть и обратную задачу: по известному значению F(x)= βn найти соответствующее ему значение xn. Геометрическая интерпретация процедуры представлена на рис.1.
Отсюда вытекает способ генерирования случайной величины, распределенной по заданному закону p(x):
1. Генерируется случайная величина βn, равномерно распределенная на интервале
 |
2. Решается интегральное уравнение относительно верхнего предела xn
Найденное значение и будет случайной величиной с плотностью распределения вероятностей p(x).
Если случайная величина может быть только положительной, т. е.
называется распределением Релея.
Математическое ожидание для распределения Релея Μρ=1.253σ
(Здесь σ – параметр распределения).

Математическая интерпретация величин с плотностью распределения вероятностей по закону Релея заключается в следующем:.
— геометрическая сумма случайных величин x и y, состоящих в квадратуре (длина вектора), и каждая из них распределена по нормальному закону с характеристиками:
математическое ожидание Mx = My = 0
дает вектор ρ, то длина которого и будет распределена по закону Релея.
Угол наклона вектора — фаза α распределена равномерно в интервале (0…2π).
 |
Рис.3. Геометрическая интерпретация распределения по закону Релея.
Для пояснения, какое отношение распределение Релея имеет к радиотехнике, напомним структуру корреляционного приемника с квадратурными каналами для приема сигналов с неизвестной начальной фазой (рис.4).
Рис.4. Корреляционный приемник с квадратурными каналами.
Операции перемножения и интегрирования являются линейными операциями по отношению к входному воздействию и не изменяют закон распределения случайного сигнала на входе.
Если на входе y(t) = n(t), т. е. действует только помеха типа «белый шум» (плотность распределения вероятностей мгновенных значений такой помехи подчиняется нормальному закону), то и значения корреляционных интегралов на выходах каналов z1 и z2 также распределены по нормальному закону. Перемножение входной помехи на опорные косинусный и синусный сигналы и обеспечивают квадратурность случайных величин z1 и z2, а операция
 |
соответствует вычислению длины вектора, т. е. геометрической (векторной) суммы случайных величин. Следовательно, при действии на входе приемника только помехи типа «белый шум» значения корреляционного интеграла z и будут распределены по закону Релея.
Если же на входе квадратурного приемника действует смесь сигнал + помеха
(сигнал us(t) частоты ω0 с неизвестной начальной фазой),
то распределения величин z1 и z2, по прежнему подчиняясь нормальному закону, будут содержать средние значения – математические ожидания μ1 и μ2, отличные от 0, обусловленные неслучайным характером полезного сигнала.
В этом случае корреляционный интеграл на выходе z подчиняется обобщенному распределению Релея (Релея – Райса):
 |

— значение сигнала на выходе приемника;
— среднеквадратическое отклонение значения помехи на выходе;
— модифицированная функция Бесселя первого рода нулевого порядка.
Примечание: значение функции Бесселя I(0)=1.
Следовательно, при отсутствии полезного сигнала на входе (μ=0) выражение для обобщенного закона Релея (2) аналитически соответствует выражению (1).Т. е. обобщенный закон Релея (2) можно применять в расчетах не только при условии, когда на входе приемника действует смесь сигнал + помеха, но и когда только помеха типа «белый шум».
 |
Рис.5. Плотность вероятности при обобщенном распределении Релея при σZ=1 и при различных значениях сигнала μ.
 |
Плотность распределения для закона Релея p(ρ) (1) интегрируема; функция распределения для закона Релея равна:
Следовательно, для формирования случайной величины, распределенной по закону Релея (например, значения сигнала на выходе квадратурного корреляционного приемника) возможно применение метода обратной функции:
где βn – случайная величина, равномерно распределенная на интервале (0…1).
В Mathcad случайная величина с равномерным распределением на интервале [0…b] формируется с помощью встроенной функции rnd(b).
Тогда выражение для формирования случайной величины, распределенной по закону Релея, принимает вид d Mathcad:
 |
(здесь вместо обозначения случайной величины ρ использовано обозначение помехи как функции времени, т. е. вектора от t).
Рис.6. Имитация помехи, распределенной по закону Релея при σ=1 (помеха на выходе квадратурного корреляционного приемника).
4. Формирование случайных величин, распределенных по нормальному закону
Нормальный закон распределения вероятностей имеет важнейшее значение. Именно нормальному закону подчиняется распределение вероятностей мгновенных значений помехи типа «белый шум».
Плотность вероятностей случайной величины x, распределенной по нормальному закону (закону Гаусса), описывается выражением:
μ
 |
– Mx — математическое ожидание (среднее значение) величины x;
σ – среднеквадратическое отклонение величины x;

Рис.7. Нормальное распределение случайной величины x (при μ=1).
Однако функция p(x) для нормального закона не интегрируема. Поэтому для формирования случайных величин, распределенных по нормальному закону, рассмотренный выше метод обратной функции не может быть применен.
4.1. Способ 1 (суммирование случайных величин).
Формирование случайных величин, распределенных по нормальному закону, можно выполнить на основании центральной предельной теоремы теории вероятностей:
распределение вероятностей величины x,
 |
равной сумме n независимых случайных величин βi
с произвольным законом распределения и мало различающимися дисперсиями (т. е. дающими примерно одинаковый вклад в общую сумму) при n → ∞ асимптотически стремится к нормальному закону.
Если величины βi распределены равномерно на интервале [0…1], то:
— математическое ожидание случайной величины x равно Mx=n/2;
— дисперсия равна Dx=n/12.
 |
На практике уже при n>=8 распределение формируемой таким образом случайной величины x достаточно близко к нормальному.
Если при формировании случайной величины выполнить нормирование:
то, x будет распределено по нормированному нормальному закону с Mx=0 и Dx=σ=1.
4.2. Способ 2 (метод полярных координат).
Случайные величины с нормальным законом распределения могут быть сформированы на основе распределения Релея (иначе данный способ называется методом полярных координат).
Для этого следует сгенерировать два случайных числа β1 и β2, равномерно распределенных на интервале [0…1], и сформировать вектор, длина которого ρ
будет распределена по релеевскому закону с параметром σ,
 |
а фаза
 |
равномерно распределена на интервале [0…2π].
Тогда в соответствии с определением закона Релея любая проекция вектора на координатные оси x или y будет распределена по нормальному закону с математическим ожиданием, равным 0, и среднеквадратическим отклонением, равным σ. (При σ=1 – нормированное нормальное распределение).
Следовательно, в качестве случайной величины может быть использована любая величин, распределенной по нормальному закону, (представлены в виде формул Mathcad):
 |
Здесь случайные величины x y также представлены в виде векторов от параметра t.
В Mathcad имеется ряд встроенных функций для генерации случайных величин, в том числе и распределенных по нормальному закону:
Функция возвращает вектор случайных чисел n размерностью N, распределенных по нормальному закону с параметрами:
— математическое ожидание равно – μ;
— среднеквадратическое отклонение — σ.
Очевидно, в Mathcad функция rnorm реализована по методу полярных координат, который хотя и требует больших вычислительных затрат, но обеспечивает более точное вычисление величин, распределенных по нормальному закону.
 |
Рис.8. Пример генерации случайных величин, распределенных по нормальному закону
(помеха типа «белый шум» — вектор n).
5. Характеристики случайных величин
Для оценки распределения случайных величин используются числовые характеристики, основными из которых являются математическое ожидание и дисперсия.
Теоретически числовые характеристики случайной величины x вычисляются путем усреднения по множеству возможных значений с учетом вероятностей их появления, для чего необходимо знать распределение вероятностей:
— для непрерывных случайных величин:
 |
— для дискретных случайных величин:
где xk – k-ое значение случайной величины; pk – вероятность k-ого значения величины x.
Применимо к рассматриваемому вопросу генерации случайных величин — помех числовые характеристики распределения могут быть рассчитаны по результатам реализации (апостериорные характеристики распределения).
Так, для сформированной последовательности случайных чисел — вектору n размерностью T математическое ожидание и дисперсия рассчитываются следующим образом:
 |  |
В Mathcad имеются встроенные функции для вычисления указанных характеристик по вектору:
— mean(n)=Mn – математическое ожидание (среднее значение);
— stdev(n) – среднеквадратическое отклонение (корень квадратный из var(n)).
расчет которых и выполняется по приведенным выше формулам.
Кроме вычисления основных характеристик Mn и Dn, по результатам реализации может быть построена гистограмма, которая позволяет сравнить распределение апостериорных вероятностей появления значений случайной величины с предполагаемым теоретическим распределением.
Для построения гистограммы по реализации случайной величины n (вектора), следует диапазон возможных значений n (n_min…n_max) разбить на дискреты Δn и вычислить число попаданий значений n в соответствующий дискрет.
В Mathcad имеется встроенная функция, которая и позволяет строить гистограммы:
— n – вектор случайной величины, по которой вычисляется гистограмма;
— W – вектор значений разбиения случайной величины (вектора) n на дискреты.
Функция hist – возвращает число значений вектора n, попавших в соответствующий дискрет Δn диапазона значений n. Если выполнить нормировку:
(T – число элементов вектора n)
то h и будет отображать апостериорные вероятности (частоту появления).
Следовательно, для построения гистограммы по полученному вектору n, например, по сгенерированной последовательности случайных величин, необходимо предварительно описать вектор W:

— индексация элементов вектора W;
max(n) min(n) – встроенные функции пакета для вычисления максимального и минимального значений вектора (матрицы).
— дискрет разбиения значений случайной величины n
— значения вектора W
После описания вектора W можно воспользоваться функцией hist и построить гистограммы:

Рис.9. Гистограмма случайной величины n (помехи типа «белый шум») при μ=0 σ=1.
Гистограмма h – вектор, индексы которого обозначены k, поэтому и гистограмму следует строить как функцию от k. Однако по оси x можно задать и значения вектора Wk для отображения значений случайной величины n.
Для сравнения гистограммы с теоретической плотностью распределения вероятностей на графике можно построить и p(k) (здесь для построения плотности распределения случайной величиной следует считать k). При этом следует вычислить соответствующие k значения математического ожидания и дисперсии (СКО).

— среднеквадратическое отклонение распределения p(k)
(σ – СКО, заданное при формировании вектора случайных величин n).
— нормальный закон для наложения на гистограмму.
Результат наложения распределения p(k) на гистограмму см. рис.9.
🎦 Видео
7. MathCad. Векторы и матрицыСкачать

Векторная диаграмма токов в программе MathcadСкачать

Mathcad Prime. Урок 7 - Статистические функции MathcadСкачать

МАТКАД МатрицыСкачать
1. MathCad. Вычисление значений числовых выраженийСкачать

Программа MathCAD. Урок 10. Работа с матрицами в MathCADСкачать

Комплексные числа в программе MathCadСкачать

rand. srand. rand задать диапазон. srand time null. Генератора случайных чисел. randomize. Урок #29.Скачать

Дискретные переменные в MathCAD 14 (9/34)Скачать

Матрицы в Mathcad(создание и редактирование матриц)(Урок 3.1)Скачать
случайные числа и процессыСкачать
9 Анализ данных MathcadСкачать

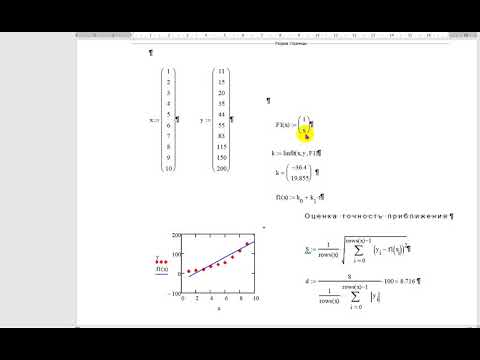
Аппроксимация данніх в MathcadСкачать
MathCAD График функции пользователя с условиемСкачать

Программирование в Mathcad 13. Написание простейших циклов и условий. Урок 24Скачать

Основы работы в Mathcad ГрафикиСкачать

MathCAD Поиск локальных экстремумов функцииСкачать



































