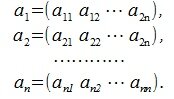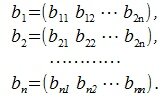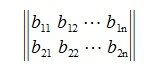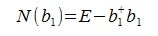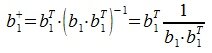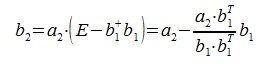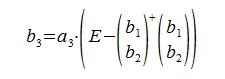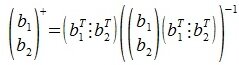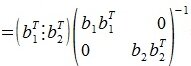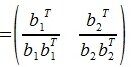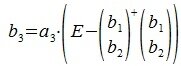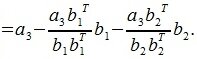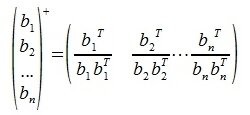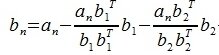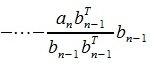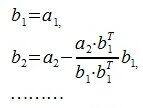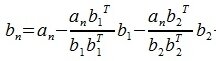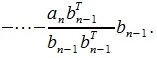Квадратная матрица 
где E — единичная матрица, A T — транспонированная матрица.
Из условия AA T =E следует, что A T является обратной к матрице A:
Для любой невырожденной квадратной матрицы можно построить ортогональную матрицу. Для построения ортогональной матрицы применяют метод ортогонализации Грамма-Шмидта. Затем нормируют полученные векторы строки. Эти две процедуры вместе называют методом ортонормализации Грамма-Шмидта.
- Ортогонализация Грамма-Шмидта
- Ортонормализация Грамма-Шмидта
- Процесс ортогонализации Грама-Шмидта
- Примеры решения задач
- Участник:KibAndrey/Ортогонализация Грама-Шмидта
- Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
Видео:A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

Ортогонализация Грамма-Шмидта
Пусть задана некоторая квадратная матрица, строки которой являются векторы
и пусть эти векторы линейно независимы (т.е. матрица построенная этими векторами строками невырождена). Требуется получить взаимно ортогональные n векторы
Суть метода заключается в следующем:
1. Выбирается некоторая строка (пусть это будет a1). b1 выбирается равным a1.
3. Вектор b3 получается проектированием a3 на нуль-пространство матрицы
Рассмотрим подробнее процесс ортогонализации.
На втором шаге вычисляем нуль-пространство b1:
где E- единичная матрица порядка nxn,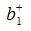
Для пректирования a 2 на нуль-пространство b 1 вычисляем
На третьем шаге вычисляем b 3:
Так как векторы b 1 и b 2 ортогональны, то
Для n -го вектора получим:
Таким образом, процедура ортогонализации Грамма-Шмидта имеет следующий вид:
Видео:Лекция 5.7. Ортогонализация Грама-Шмидта: примерСкачать

Ортонормализация Грамма-Шмидта
Суть метода ортонормализации Грамма-Шмидта заключается в ортогонализации методом Грамма-Шмидта а затем нормализации полученных векторов строк:
Видео:Процесс ортогонализации Грама-Шмидта. ПримерСкачать

Процесс ортогонализации Грама-Шмидта
Определение. Векторы $a$ и $b$ называются ортогональными, если их скалярное произведение равно нулю.$$left(a, bright)=0.$$
Определение. Системы $S_ = langle a_,a_,…,a_rangle,$ и $S_ = langle b_,b_,…,b_rangle,$ называются эквивалентными, когда векторы каждой из систем, линейно выражаются через векторы, другой системы.
Теорема. Допустим, у нас есть линейно независимая система $S = langle a_,a_,ldots,a_rangle.$ Тогда всегда найдется такая система $S_ = langle b_,b_,…,b_rangle,$ которая будет эквивалентной и ортогональной к $S,$ которая получается следующим методом:
Докажем же существование $S_$ эквивалентной $S$ с помощью индукции. При $k = 1$ $$b_ = a_.$$ При $k = 2$ $$left(b_, b_right) = left(a_ + lambda_b_, b_right) = left(a_, b_right) + lambda_left(b_, b_right) =$$$$= left(a_, b_right)-dfrac<left(a_, b_right)><left(b_, b_right)>left(b_, b_right) = 0.$$ Из чего очевидно, что $S = langle a_,a_rangle$ и $S_ = langle b_,b_rangle$ — эквивалентны.
Теперь докажем для $k = m,$ при $2leqslant jleqslant k$ $$left(b_, b_right) = left(a_ + sumlimits_^lambda_b_, b_right) = left(a_, b_right) + sumlimits_^lambda_left(b_, b_right) =$$$$= left(a_, b_right)-sumlimits_^dfrac<left(a_, b_right)><left(b_, b_right)>left(b_, b_right) = 0.$$ Как видим, по индукции мы доказали, что любой ЛНЗ системе, методом Грама-Шмидта, можно найти эквивалентную ей ортогональную систему.
Видео:Лекция 5.8. Ортогонализация Грама-ШмидтаСкачать

Примеры решения задач
Рассмотрим примеры задач, в которых может использоваться процесс ортогонализации Грама-Шмидта. Постарайтесь решить данные примеры самостоятельно, а затем сверить свое решение с приведенным.
- Применяя процесс ортогонализации по Грамму-Шмидту построить ортогональный базис подпространства, натянутого на данную систему векторов $S = langle a_, a_, a_rangle.$
$$a_ = (1, 2, 2, -1), a_ = (1, 1, -5, 3), a_ = (3, 2, 8, -7).$$
Первым делом, найдем $b_$. В первом пункте пишется, что $b_ = a_.$
Дальше найдем $b_.$ Из формулы пункта 2), мы видим, что: $$b_ = a_ + lambda_ cdot b_, lambda_ = dfrac<left(a_, b_right)><left(b_, b_right)>,$$ все необходимое для решения мы нашли, осталось только решить. Итак:$$lambda_ = -dfrac<left(a_, b_right)><left(b_, b_right)> = -dfrac = -left(dfracright) = 1,$$ лямбду мы нашли, $b_$ у нас есть, теперь мы можем найти $b_:$ $$b_ = a_ + lambda_cdot b_ = (1, 1, -5, 3) + (1, 2, 2, -1) = (2, 3, -3, 2).$$
Выпишем же формулу для $b_:$ $$b_ = a_ + lambda_ cdot b_ + lambda_ cdot b_,$$ при $$lambda_ = -dfrac<left(a_, b_right)><left(b_, b_right)>,quad lambda_ = -dfrac<left(a_, b_right)><left(b_, b_right)>,$$ найдем все необходимое: $$lambda_ = -dfrac= -3,$$ $$lambda_ = -dfrac= 1.$$ Теперь вычислим $b_:$ $$b_ = (3, 2, 8, -7)-3(1, 2, 2, -1) + 1(2, 3, -3, 2) = (2, -1, -1, 2).$$
Получили ортогональный базис $S_ = langle b_, b_, b_rangle$ — систему, эквивалентную данной, $S = langle a_, a_, a_rangle.$ $$S_ = langle (1, 2, 2, -1), (2, 3, -3, 2), (2, -1, -1, 2)rangle.$$
Применяя процесс ортогонализации по Грамму-Шмидту построить ортогональный базис подпространства, натянутого на данную систему векторов $S = langle a_, a_, a_rangle.$
$$a_ = (1, 1, -1, -2), a_ = (5, 8, -2, -3), a_ = (3, 9, 3, 8).$$
Первым делом, найдем $b_$, $b_ = a_.$
Дальше найдем $b_.$ Из формулы пункта 2) мы видим, что: $$b_ = a_ + lambda_ cdot b_, lambda_ = dfrac<left(a_, b_right)><left(b_, b_right)>,$$ все необходимое для решения мы нашли, осталось только решить. Итак:$$lambda_ = -dfrac = -left(dfracright) = 3,$$ лямбду мы нашли, $b_$ у нас есть, теперь мы можем найти $b_:$ $$b_ = a_ + lambda_cdot b_ = (5, 8, -2, -3) + (-3, -3, 3, 6) = (2, 5, 1, 3).$$
Видео:Ортогонализация Грама Шмидта 1361Скачать

Участник:KibAndrey/Ортогонализация Грама-Шмидта
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Frolov и ASA. |
| Ортогонализация Грама-Шмидта | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]Oleft(k^2nright)[/math] |
| Объём входных данных | [math]kn[/math] |
| Объём выходных данных | [math]kn[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(kn)[/math] |
| Ширина ярусно-параллельной формы | [math]O(kn)[/math] |
Все пункты данной статьи обсуждались и создавались совместно, доля ответственности равноправна.
Видео:Процесс ортогонализации Грама-Шмидта. ТемаСкачать

Содержание
Видео:§48 Ортонормированный базис евклидова пространстваСкачать

1 Свойства и структура алгоритма
Видео:Ортогонализация Грама-Шмидта, ортонормированный базис | 27 | Константин Правдин | ИТМОСкачать

1.1 Общее описание алгоритма
Процесс ортогонализации Грама–Шмидта [1] — алгоритм построения ортогональной системы ненулевых векторов по (данной) линейно независимой системе векторов из евклидова или эрмитова пространства V, при котором каждый вектор построенной системы линейно выражается через векторы исходной системы пространства V.
Процесс ортогонализации Грама-Шмидта может быть применен к любой, в том числе и линейно-зависимой системе элементов евклидова пространства. Если ортогонализуемая система линейно-зависима, то на некотором шаге (возможно несколько раз) мы получим нулевой элемент, после отбрасывания которого можно продолжить процесс ортогонализации [2] , однако в данной статье этот случай мы не рассматриваем.
Исторически это первый алгоритм, описывающий процесс ортогонализации. Традиционно его связывают с именами Йоргена Педерсена Грама и Эрхарда Шмидта. Йорган Педерсен Грам [3] был датским актуарием (специалистом по страховой математике, на современном языке это профессия финансового аналитика), который в неявном виде представил суть процесса ортогонализации в 1883 году [4] . Нельзя не сказать о том, что метод ортогонализации в несколько ином, модифицированом виде, ранее использовал Пьер-Симон Лаплас при нахождении массы Сатурна и Юпитера из систем нормальных уравнений и расчете распределения ошибок при этих вычислениях [5] . Ясно, что Й. Грам не знал о том, что Лаплас ранее использовал этот метод. Эрхард Шмидт [3] был учеником великих математиков Германа Шварца и Давида Гильберта. Алгоритм ортогонализации был опубликован Э. Шмидтом в 1907 году в его исследовании интегральных уравнений [6] , которое в свою очередь дало основание для развития теории гильбертовых пространств. Шмидт, используя процесс ортогонализации применительно к геометрии гильбертова пространства решений интегральных уравнений, отмечал, что процесс ортогонализации принципиально такой же, какой прежде использовал Й. Грам. В отечественной литературе иногда этот процесс называют ортогонализацией Сонина–Шмидта [7] [8] . Это название связано с тем, что разработанный Сониным [9] метод ортогонализации системы функций для частного случая по существу не отличается от метода ортогонализации системы функций, предложенного ранее Шмидтом [6] .
Процесс ортоганализации Грама-Шмидта лежит в основе многих алгоритмов вычислительной математики. Классический процесс ортогонализации Грама–Шмидта применяется в таких современных областях науки, как анализ изображений [10] , цифровая обработка сигналов [11] , нейронные сети [12] .
Видео:10 5 Процесс ортогонализацииСкачать

1.2 Математическое описание алгоритма
Пусть [math]V[/math] — евклидово пространство размерности [math]n[/math] .
[math]k[/math] линейно независимых векторов [math]mathbf,mathbf,ldots,mathbf[/math] пространства [math]V[/math] .
[math]k[/math] ортогональных векторов [math]mathbf,mathbf. mathbf[/math] пространства [math]V[/math] , причем [math]mathbf=mathbf[/math] , либо
[math]k[/math] ортонормированных векторов [math]mathbf,mathbf
,ldots,mathbf
[/math] пространства [math]V[/math] , причем [math]mathbf
=frac<mathbf><|mathbf|>[/math] , [math]i=1,2, ldots,k[/math] .
Формулы процесса ортогонализации:
Здесь [math]proj_<mathbf>mathbf<a_>[/math] , для [math]j=1. k-1[/math] — это модуль проекции вектора [math]mathbf<a_>[/math] на ось, проходящую через вектор [math]mathbf[/math] .
Формула для ее вычисления, полученная из определения скалярного произведения: [math]proj_<mathbf>mathbf<a_>=dfrac<(mathbf<a_>,mathbf<b_>)><mathbf<left|mathbfright|>>[/math] , для [math]j=1. i-1[/math] .
Произведение длин [math]mathbf,mathbf,ldots ,mathbf[/math] равно объему параллелепипеда, построенного на векторах системы [math]left<mathbfright>[/math] , [math]i=1,2,ldots ,k[/math] , как на ребрах.
Явное выражение векторов [math]mathbf[/math] для [math]i=1. k[/math] через [math]mathbf,mathbf. mathbf[/math] дает формула
[math] mathbf= begin (a_1,a_1) & cdots & (a_1,a_i-1) &a_1 \ (a_,a_1) & cdots & (a_2,a_i-1) &a_2 \ cdots & cdots & cdots& cdots \ (a_,a_1) & cdots & (a_i,a_i-1) &a_i \ end [/math] . (В правой части этого равенства определитель следует формально разложить по последнему столбцу).
Иногда полученные векторы нормируются сразу после их нахождения и находится система ортонормированных векторов [math]mathbf,mathbf
,ldots,mathbf
[/math] . В этом случае в знаменателе при вычеслении проекции по формуле будет [math]|mathbf
|=1[/math] для [math]i=1. k-1[/math] , что существенно упрощает вычисления алгоритма. В настоящей статье применяя процесс ортогонализации к системе линейно независимых векторов, мы так и будем поступать.
Если в описанном алгоритме в формулах для вычисления векторов [math]mathbf,[/math] , для [math]i=1. k[/math] процесса ортогонализации заменить [math]proj_<mathbf>mathbf<a_>[/math] , для [math]j=1. i-1[/math] на [math]proj_<mathbf>mathbf<b_>[/math] , для [math]j=1. i-1[/math] , алгоритм, полученный таким образом называется модифицированным алгоритмом Грама–Шмидта.
Чаще всего, процесс Грама–Шмидта приводит к значительному нарушению ортогональности. Что касается модифицированного процесса Грама–Шмидта, он проявляет себя достаточно неусточиво, хоть и чуть менее, чем классический процесс.
Видео:Евклидовы пространства Метод ортогонализации ШмидтаСкачать

1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма состоит из вычисления:
включая нахождения скалярных произведений одинаковых векторов дальнейшего нахождения их длин;
- [math]dfrac[/math] умножений векторов на число после вычисления нового базисного вектора на итерации.
Видео:Метод ортогонализации Грама-Шмидта. Семинар 24Скачать
1.4 Макроструктура алгоритма
Как уже отмечено в описании вычислительного ядра алгоритма, основную часть метода составляют вычисления скалярных произведений, как для вычисления длины очередного вектора, так и для расчета проекций прочих векторов на новый вектор, а также умножения векторов на числа, используемые при корректировке значений остальных векторов после вычисления очередного вектора, ортогонального предыдущим.
Таким образом, основновные макрооперации алгоритма:
- вычисления скалярных произведений,
- умножения векторов на числа, используемые при корректировке значений остальных векторов после вычисления очередного вектора, ортогонального предыдущим.
Теперь опишем макроструктуру процесса ортогонализации. На верхнем уровне она представляет из себя последовательное вычисление [math]k[/math] ортонормированных векторов [math]mathbf,mathbf
,ldots,mathbf
,ldots,mathbf
[/math] .
2. При [math]i=2. k[/math] :
Видео:Процесс ортогонализации Грама-Шмидта. ОтветыСкачать

1.5 Схема реализации последовательного алгоритма
Входные данные: [math]k[/math] линейно независимых векторов [math]mathbf,mathbf,ldots,mathbf[/math] длины [math]n[/math] [math]left(alpha_right.[/math] , где [math]j=1,2, ldots,n[/math] — координаты вектора [math]mathbf[/math] , для [math]left.i=1,2, ldots,kright)[/math] .
[math]k[/math] ортогональных векторов [math]mathbf,mathbf. mathbf[/math] длины [math]n[/math] [math]left(beta_right.[/math] , где [math]j=1,2, ldots,n[/math] — координаты вектора [math]mathbf[/math] , для [math]left.i=1,2, ldots,kright)[/math] , причем [math]mathbf=mathbf[/math] , либо
[math]k[/math] ортонормированных векторов [math]mathbf,mathbf
,ldots,mathbf
[/math] длины [math]n[/math] ( [math]gamma_[/math] , [math]j=1,2, ldots,n[/math] — координаты вектора [math]mathbf
[/math] , для [math]left.i=1,2, ldots,kright)[/math] , причем [math]mathbf
=frac<mathbf><|mathbf|>[/math] , для [math]i=1,2, ldots,k[/math] .
Последовательность исполнения метода:
2. При [math]i[/math] от [math]1[/math] до [math]n[/math] :
3. При [math]i[/math] от [math]2[/math] до [math]k[/math] :
при [math]j[/math] от [math]1[/math] до [math]n[/math] : [math]beta_=alpha_-sumlimits_^left(sumlimits_^n alpha_gamma_right)gamma_ [/math] [math]|mathbf|=sqrt<beta_^2+beta_^2+ldots+beta_^2>[/math] при [math]j[/math] от [math]1[/math] до [math]n[/math] : [math]gamma_= frac<beta_><|mathbf<b_>|>[/math] .
Видео:Ортогональные системы векторов. Процесс ортогонализации (задача 1357)Скачать

1.6 Последовательная сложность алгоритма
Для ортогонализации [math]k[/math] линейно независимых векторов длины [math]n[/math] в последовательном варианте с помощью классического метода ортогонализации Грама–Шмидта потребуется:
- [math]k[/math] вычислений квадратного корня
- [math]frac[/math] сложений,
- [math]frac[/math] вычитаний,
- [math]k^2 n[/math] умножений,
- [math]k n[/math] делений.
Умножения, сложения и вычитания составляют основную часть алгоритма.
При классификации по последовательной сложности, таким образом, метода ортогонализации Грама–Шмидта с кубической сложностью.
Видео:10. Ортогонализация с помощью процедуры Грама ШмидтаСкачать
1.7 Информационный граф
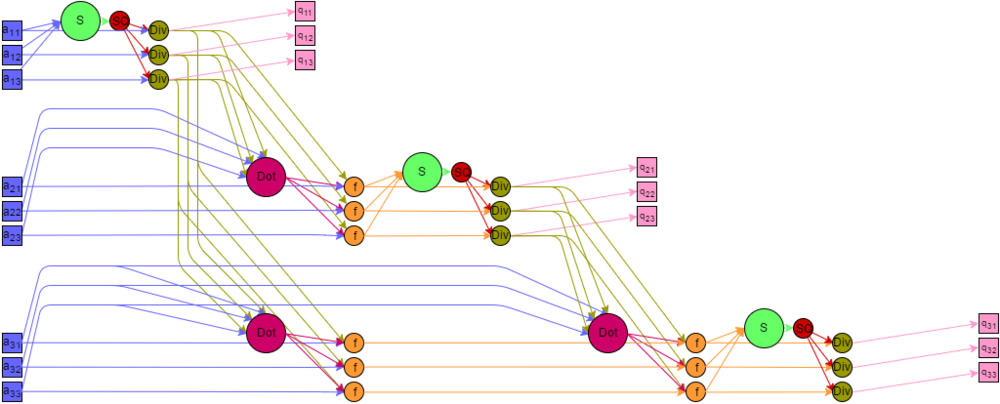
Представим граф алгоритма [13] [14] [15] с помощью текстового описания, а также с помощью изображения.
Все вершины графа можно разбить на пять групп, каждой из которых соответствует вид исполняемой операции. Каждая вершина расположена в точках с целочисленными координатами, в пространствах с числом измерений от [math]1[/math] до [math]3[/math] . Дадим описание каждой из групп.
Первая группа — вершины, которым соответствует операция скалярного умножения вектора на себя. На графе они располагаются в одномерной области. [math]i[/math] изменяется от [math]1[/math] до [math]k[/math] .
Значениями аргументов для этих функций являются:
- при [math]i = 1[/math] — входные данные [math]<a_>, p = 1..n[/math] ;
- при [math]i gt 1[/math] — результат выполнения функции в вершине пятой группы с координатами [math], p = 1..n[/math] .
Результат этих операций является промежуточным данным алгоритма.
Вторая группа — вершины, которым соответствует операция SQRT извлечения квадратного корня. Они расположены в одномерной области, [math]i [/math] изменяется от [math]1[/math] до [math]k[/math] .
Значением аргумента для этих функций является результат выполнения функции в вершине первой группы, с координатой [math]i[/math] .
Результат является промежуточным данным алгоритма.
Третья группа — вершины, которым соответствует операция деления. Располагаются в двумерной области, [math]i[/math] изменяется от [math]1[/math] до [math]k[/math] , [math]p[/math] изменяется от [math]1[/math] до [math]n[/math] .
Значениями аргументов для этих функций являются:
- делимое:
- при [math]i = 1[/math] — входные данные [math]a_[/math] ;
- при [math]i gt 1[/math] — результат выполнения функции в вершине пятой группы с координатами [math]i-1,1,p[/math] ;
- делитель — результат выполнения функции в вершине второй группы с координатой [math]i[/math] .
Результат является выходным данным алгоритма [math]q_[/math] .
Значениями аргументов для этих функций являются:
Результат является промежуточным данным алгоритма.
Пятая группа — вершины которые соответствуют операции [math]a — b c[/math] . Располагаются в трехмерной области, [math]i[/math] изменяется от [math]1[/math] до [math]k-1[/math] , [math]j[/math] изменяется от [math]1[/math] до [math]k-i[/math] , [math]p[/math] изменяется от [math]1[/math] до [math]n[/math] .
Значениями аргументов для этих функций являются:
- [math]a[/math] :
- при [math]i = 1[/math] — входные данные [math]a_[/math] ;
- при [math]i gt 1[/math] — результат выполнения функции в вершине пятой группы с координатами [math]i-1,j+1,p[/math] ;
- [math]b[/math] — результат выполнения функции в вершине четвертой группы, с координатами [math]i,j[/math] ;
- [math]c[/math] — результат выполнения функции в вершине третьей группы с координатой [math]i,p[/math] .
Результат является промежуточным данным алгоритма.
Описанный граф для случая [math]k = 3[/math] , [math]n = 3[/math] изображен на рисунке. Каждая группа вершин отличается цветом и буквенным обозначением. «S» — первая группа, «SQ» — вторая группа, «Div» — третья группа, «Dot» — четвертая группа, «f» — пятая группа. Квадратные метки синего и розового цветов обозначают передачу входных и выходных данных соответственно.
Видео:Как разложить вектор по базису - bezbotvyСкачать

1.8 Ресурс параллелизма алгоритма
Для построения ортонормированного базиса методом Грама–Шмидта необходимо выполнить следующие ярусы операций:
- [math]k[/math] ярусов вычисления скалярных произведений векторов на самих себя (по одной операций на каждом, сложность операции по высоте и по ширине ЯПФ — [math]O(n)[/math] и [math]O(1)[/math] соответственно);
- [math]k[/math] ярусов вычисления квадратного корня (по одной операции на каждом);
- [math]k[/math] ярусов деления (по [math]n[/math] операций на каждом);
- [math]k-1[/math] ярус вычисления скалярных произведений пары векторов (от [math]1[/math] до [math](k-1)[/math] операций на каждом,сложность операции по высоте ЯПФ — O(n), по ширине — O(1));
- [math]k-1[/math] ярус умножения/вычитания чисел (от [math]n[/math] до [math](k-1)n[/math] операций на каждом).
В этом случае сложность алгоритма при классификации по высоте ЯПФ — [math]O(kn)[/math] , при классификации по ширине ЯПФ — [math]O(kn)[/math] .
Видео:Процесс ортогонализации Грама-Шмидта. Еще один примерСкачать

1.9 Входные и выходные данные алгоритма
Входные данные: матрица [math]A[/math] с элементами [math]alpha_[/math] , где [math]i[/math] принимает значения [math]1,ldots,k[/math] , [math]j[/math] принимает значения [math] 1,ldots,n[/math] . Здесь [math]kleqslant n[/math] . По строкам этой матрицы записаны [math]k[/math] линейно-независимых векторов некоторого пространства размерности [math]n[/math] .
Объем входных данных: [math]kn[/math] .
Выходные данные: матрица [math]Q[/math] с элементами [math]gamma_[/math] . Строки этой матрицы также задают [math]k[/math] векторов единичной длины размерности [math]n[/math] , причем всякое скалярное произведение двух различных векторов этой системы равно [math]0[/math] .
Объем выходных данных: [math]kn[/math] .
Замечание: Алгоритм может работать с вырожденной матрицей, он выдаёт нулевую строку на шаге [math]j[/math] , если строка [math]j[/math] матрицы [math]A[/math] является линейной комбинацией предыдущих строк. В этом случае для корректного продолжения работы алгоритма необходима дополнительная проверка на равенство строки нулю и пропуск соответствующих строк. Количество построенных векторов будет равняться размерности пространства, порождаемого строками матрицы.
Видео:Линейная алгебра Практика 16 Процесс ортогонализации Грама Шмидта Ортогональный оператор ПриведеСкачать

1.10 Свойства алгоритма
Отношение последовательной и параллельной сложности алгоритма в случае неограниченных ресурсов равно [math]dfrac=k[/math] . Вычислительная мощность алгоритма линейная.
Алгоритм почти полностью детерминирован — единственность результата выполнения гарантирована, однако возможно накопление ошибок округления.
Алгоритм является численно неустойчивым — ошибки округления могут привести к неортогональности полученных векторов.
Большинство дуг информационного графа являются локальными. Исключение составляют дуги исходящие из операций деления и извлечения корня — для первой группы количество дуг пропорционально квадрату количества векторов, а для второй — пропорционально размерности пространства, в котором заданы эти вектора. Возникающие при это длинные дуги могут быть заменены несколькими короткими пересылками между соседями.
Видео:Тимашев Д.А. - Линейная алгебра и геометрия. Лекции - 15. Ортогонализация Грама–ШмидтаСкачать

2 Программная реализация алгоритма
Видео:Матрица ГрамаСкачать

2.1 Особенности реализации последовательного алгоритма
Видео:Евклидово пространство. Ортонормированный базис | Лекция 11 | ЛинАл | СтримСкачать
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
Анализ последовательной реализации алгоритма Грама-Шмидта с помощью инструмента callgrind показывает, что наибольшую долю [math]big([/math] более 97% для [math]k=n=512big)[/math] процессорного времени использует процесс вычитания проекций нормированного вектора от остальных векторов. Этот процесс состоит из вложенных циклов — в одном из циклов происходит итерация по векторам, а в другом — по подпространствам. Таким образом, задача допускает следующие варианты параллельных реализаций:
- Распараллеливание по векторам.
Векторы распределяются по MPI-процессам. После нормировки очередного вектора процесс рассылает его остальным с помощью процедур групповой коммуникации. В исследуемой реализации используется вызов MPI_Bcast.
- Распараллеливание по векторам (b).
Так как рассылать очередной вектор необходимо не всем процессам, а только тем, которые содержат ещё не обработанные векторы, перед вызовом Bcast можно создавать новый коммуникатор, содержащий только необходимые процессы. Оптимальность данного способа реализации не исследовалась.
- Распараллеливание по подпространствам.
Так как последовательная программа содержит операции скалярного произведения, можно назначить каждому MPI-процессу некоторое подпространство. Скалярное произведение при этом подсчитывается при помощи операции Allreduce. Данная реализация является менее оптимальной, так как содержит [math]frac[/math] операций групповой коммуникации, в отличие от k операций для предыдущих реализаций.
Недостаток параллельной реализации классического алгоритма Грама-Шмидта [16] в том, что для матриц с высоким числом обусловленности на входе, система векторов на выходе алгоритма не всегда ортогональна [17] .
Итеративно-параллельный классический алгоритм Грама-Шмидта cодержит процедуру итеративной реортогонализации, который даёт возможность избежать недостатков предыдущего метода [18] .
Блочно-параллельный алгоритм Грама-Шмидта [19] — версия параллельного алгоритма Грама-Шмидта, использующая оптимизированные по использованию кэша матричные операции [20] [21] .
2.4 Масштабируемость алгоритма и его реализации
Проводились исследования двух параллельных реализаций метода ортогонализации Грама-Шмидта с использованием OpenMP и MPI.
Код был скомпилирован gcc 4.3.2, стандарт c++11, с флагом -O3. со следующими значениями параметров:
- число процессоров [1:16] с шагом 1;
- размер матрицы [192:3072] с шагом 192.
В результате экспериментов получен следующий диапазон значений эффективности реализации алгоритма:
- минимальная эффективность реализации 0.20%;
- максимальная эффективность реализации 11.18%.
На рисунках приведены графики производительности и эффективность исследованной реализации алгоритма в зависимости от числа процессоров и размера матрицы.