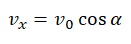Вектор скорости vx vy

Видео:Физика: Понятие Вектор, Вектор СкоростиСкачать

Vнв, Vэк, Maximum Range, Endurance и V-speeds

В данной статье разговор пойдет сразу о 8 скоростях (а точнее, восьми понятиях), использующихся в российской и зарубежной литературе по аэродинамике, и будет сделана попытка установить тождественность некоторых из них. А именно:

Vэк = Speed for Maximum Endurance = Vx (ВАОС) = Speed for Minimum Rate of Descend

Vнв = Speed for Maximum Range = Vy (ROC) = Best Glide Speed (Vbg)

Вероятно, вы уже пытались разобраться в этих скоростях самостоятельно, читая авиационные форумы и разнообразные сайты в интернете. Как говорил известный персонаж Леонида Броневого: «Верить в наше время нельзя никому. Иногда даже самому себе. Мне – можно». 🙂

К сожалению, практически все форумные дискуссии на данную, довольно непростую, тему быстро переходят от аэродинамики на личности оппонентов. Искать крупицы истины в помоях, которыми незнакомые и часто малоквалифицированные люди поливают друг друга, занятие утомительное и малопродуктивное.

На самом деле, речь идет об установлении соответствия между принятыми российскими и западными терминами. Так как российская и западная школы много лет развивались обособленно друг от друга, было бы логично искать информацию по обе стороны океана. Чем я и занимался, упорно выедая мозг всем знакомым летчикам и инструкторам в Канаде на заданную тему. И знаете что? Мозг у людей здесь какой-то невкусный. 🙂 Нелюбопытные они. И хотя некоторая полезная информация была получена, ясной картины все не складывалось.

Я начал думать, что если даже весьма опытные и заслуженные летчики не знают ответа на такой популярный вопрос, то, может быть, это и есть тот самый «magic», объясняющий, почему самолет летает, а крыльями не машет?

Рис. 1: Magic

Однажды я поделился своими сомнениями с Павлом Юрьевичем Калугиным, моим российским инструктором. Он меня сразу разочаровал, сказав, что чудес на свете не бывает, а бывает «Практическая Аэродинамика». Я задал ему тысячу вопросов (большинство из них – глупые) и получил ответы почти на все. Кроме этого, он снабдил меня соответствующей литературой. На основе всего этого была написана статья, которую вы читаете. Она содержит точные ссылки на использованные источники с указанием номеров страниц. При желании вы можете сами убедиться, что я не выдумал ничего нового, а только собрал разрозненные сведения воедино.

ВНИМАНИЕ: все нижесказанное справедливо только для самолетов с поршневыми двигателями. Аэродинамика самолетов с реактивными силовыми установками имеет массу принципиальных отличий. Вы сможете о них прочитать самостоятельно в приведенном мной учебнике А.А. Жаброва или других источниках.

Вообще говоря, выдумывать что-то новое и не требовалось. Все уже придумано выдающимися учеными прошлого, в частности, профессором Николаем Егоровичем Жуковским (1847 -1921), создавшим аэродинамику как науку. И хотя его огромный вклад в развитие авиации старательно замалчивается на Западе, предложенный им графо-аналитический метод анализа летных данных самолета (т.н. «кривые Жуковского») живет и побеждает.

Рис. 2: Н.Е. Жуковский

Существует ДВА вида кривых Жуковского (кривые тяг и мощностей). Вся хитрость в том, что рассматривать эти кривые нужно одновременно, имея возможность сопоставлять их друг с другом. Это будет сделано ниже, но начнем мы с аэродинамического сопротивления самолета.

ПОЛНОЕ АЭРОДИНАМИЧЕСКОЕ СОПРОТИВЛЕНИЕ

Известно, что полное аэродинамическое сопротивление самолета складывается из его лобового и индуктивного сопротивлений.

Лобовое сопротивление (parasite drag) зависит от лобового сопротивления фюзеляжа и других элементов конструкции самолета, их взаимного аэродинамического влияния и свойств обтекаемости материала обшивки. Лобовое сопротивление РАСТЕТ по мере УВЕЛИЧЕНИЯ скорости.

Индуктивное сопротивление (induced drag) является побочным продуктом создания подъемной силы и зависит от угла атаки крыла. Чем больше угол атаки, тем сильнее вектор полной аэродинамической силы крыла отклонен назад и тем больше индуктивное сопротивление. Чем меньше угол атаки, тем меньше индуктивное сопротивление.

Поскольку для полета на бОльших скоростях требуется меньший угол атаки, индуктивное сопротивление снижается по мере увеличения скорости и РАСТЕТ по мере ее УМЕНЬШЕНИЯ.

Если сложить два вида сопротивлений, лобовое и индуктивное, то мы получим полное аэродинамическое сопротивление (total drag). Графически это выглядит следующим образом:

Рис. 3: Полное аэродинамическое сопротивление и его компоненты

Мы помним, что условием постоянства скорости в горизонтальном полете является равенство полного аэродинамического сопротивления (drag) и тяги самолета (thrust required), X = P. Действительно, чтобы скорость полета была постоянной, сила сопротивления должна преодолеваться силой тяги равной ей по величине. Поэтому рассмотренную выше кривую полного аэродинамического сопротивления можно считать также и кривой потребной тяги горизонтального полета (они равны друг другу).

НАИВЫГОДНЕЙШАЯ СКОРОСТЬ (Vнв)

Поскольку в нижней точке рассмотренной кривой полное аэродинамическое сопротивление минимально, самолету требуется минимум тяги для горизонтального полета. В этой же точке достигается максимальное качество самолета, которому соответствует наивыгоднейший угол атаки, α нв.

«Воздушная скорость, соответствующая этому углу атаки и минимальной потребной тяге называется теоретически наивыгоднейшей скоростью горизонтального полета » (Жабров А.А. Теория полета и пилотирования самолета. — М.: ДОСААФ, 1959. — С. 123.).

РЕЖИМ МАКСИМАЛЬНОЙ ДАЛЬНОСТИ (Speed for Maximum Range)

Раз при полете на наивыгоднейшей скорости требуется минимальная сила тяги, то совершаемая самолетом работа на 1 км пути минимальна, и удельный расход топлива (расход на 1 км пути) тоже должен быть минимальным. Таким образом, наивыгоднейшая скорость Vнв теоретически должна обеспечивать максимальную дальность полета. На практике, из-за того что двигатель работает с некоторыми потерями, минимальный удельный расход топлива достигается на несколько большей скорости, называемой «режимом максимальной дальности» (Жабров А.А. Теория полета и пилотирования самолета. — М.: ДОСААФ, 1959. — С. 124.).

Так как отличия рассмотренных скоростей незначительны, можно провести условное равенство между Vнв и «режимом максимальной дальности» (Speed for Maximum Range).

Vнв ≈ Speed for Maximun Range

Пришло время более подробно поговорить о кривых Жуковского. Прежде всего, как вы думаете, чего не хватает на рассмотренном выше графике потребной тяги? Чем вообще самолет отличается от планера? Правильно, наличием силовой установки. Т.е. у него есть не только потребная, но и располагаемая тяга. Именно эта кривая мистическим образом отсутствует на многих графиках в западных учебниках (как, например, на Рис. 3). Но мы исправим это упущение, воспользовавшись иллюстрациями из российской литературы. В данном случае, графиками тяг и мощностей из «Практической аэродинамики самолета Як-18Т», с которых я убрал все лишнее и добавил кое-что нужное (синим). Я также расположил графики друг над другом, приведя к единому масштабу и совместив по шкале скоростей. См. Рис. 4.

Рис. 4: Кривые Жуковского для тяг (вверху) и мощностей (внизу)

Как видно на верхнем графике, кривая располагаемой тяги Pр имеет наклон вправо. Это значит, что по мере увеличения скорости, располагаемая тяга УМЕНЬШАЕТСЯ. Что довольно странно, не правда ли?

На самом деле это объяснимо. Силовая установка неподвижного самолета производит максимальную тягу. По мере роста скорости эффективность пропеллера снижается. Он просто «не успевает цепляться» за несущийся навстречу воздух. Теоретически, при бесконечном увеличении скорости наступит момент, когда пропеллер вообще перестанет создавать тягу. При еще большей скорости уже встречный поток воздуха будет вращать двигатель, как ветряк. Подчеркну, что практически такое невозможно: и самолет, и двигатель разрушились бы значительно раньше. Но из этого примера должно быть понятно, почему тяга силовой установки уменьшается с ростом скорости.

Имейте в виду, что кривая располагаемой тяги это именно КРИВАЯ. Пусть график располагаемой тяги Як-18T, близкий к прямой линии, не вводит вас в заблуждение: это лишь частный случай и хорошая реализация винта изменяемого шага (constant speed propeller). Для силовых установок с винтами постоянного шага (такими как на Cessna 150 и Cessna 172) график располагаемой тяги имеет более затейливую форму, далекую от прямолинейной.

ПОТРЕБНАЯ И РАСПОЛАГАЕМАЯ МОЩНОСТЬ

Обратимся теперь к нижнему графику. На нем изображены кривые мощностей. Что такое мощность? Согласно определению, мощность это произведение силы (в нашем случае силы тяги) на секундную скорость. Например, в Википедии вы найдете такое определение мощности (для Механики): «скалярное произведение вектора силы на вектор скорости, с которой движется тело».

Раз так, то если мы умножим и потребную, и располагаемую тягу (Pп и Pр, верхний график) на скорость, мы получим потребную и располагаемую мощности (Nп и Nр, нижний график). Уточню, что для получения мощности в лошадиных силах результат придется также разделить на 0.75, но это уже детали.

Кривая потребной мощности говорит о том, какой минимальной мощности силовая установка нужна для достижения заданной скорости горизонтального полета. Сопоставляя с ней кривую располагаемой мощности, можно определить, какие скорости могут быть достигнуты, а также оценить избыток мощности силовой установки, имеющийся на каждой из этих скоростей.

При дальнейших рассуждениях важно помнить, что кривые мощностей являются производными от кривых тяг, чем и обусловлена «магическая взаимосвязь» обоих графиков, с которой мы столкнемся ниже.

НАИВЫГОДНЕЙШАЯ СКОРОСТЬ (Vнв.) НА КРИВЫХ ПОТРЕБНОЙ ТЯГИ И МОЩНОСТИ

Сопоставляя графики тяг и мощностей, можно увидеть, что наивыгоднейшая скорость Vнв является нижней точкой кривой потребной тяги и, одновременно, точкой перегиба кривой потребной мощности (обратите внимание на касательную, проведенную к ней из начала координат). В этой же точке, как говорилось выше, достигается минимальный удельный расход топлива (расход на 1 км пути).

ЭКОНОМИЧЕСКАЯ СКОРОСТЬ (Vэк)

На кривой потребной мощности можно найти также скорость, для полета на которой требуется минимальная мощность (нижняя точка кривой потребной мощности). Согласно определению, «скорость, соответствующая экономическому углу атаки и минимальной потребной мощности, называется экономической скоростью горизонтального полета» (Жабров А.А. Теория полета и пилотирования самолета. — М.: ДОСААФ, 1959. — С. 129.).

РЕЖИМ МАКСИМАЛЬНОЙ ПРОДОЛЖИТЕЛЬНОСТИ ПОЛЕТА (Speed for Maximum Endurance)

Поскольку при полете на экономической скорости требуется минимальная мощность, моментальный (а также и часовой) расход топлива минимален. Следовательно, экономическая скорость Vэк теоретически должна обеспечивать максимальную продолжительность полета. На практике, как мы уже знаем, двигатель работает с некоторыми потерями, поэтому минимальный часовой расход достигается на несколько большей скорости, называемой «режимом максимальной продолжительности полета» (Жабров А.А. Теория полета и пилотирования самолета. — М.: ДОСААФ, 1959. — С. 129.).

Опять же, из-за того, что отличия этих скоростей незначительны, мы можем провести условное равенство между Vэк и «режимом максимальной продолжительности полета» (Speed for Maximum Endurance).

Vэк ≈ Speed for Maximun Endurance

ЭКОНОМИЧЕСКАЯ СКОРОСТЬ (Vэк) НА КРИВЫХ ПОТРЕБНОЙ ТЯГИ

Опять вернемся к графику потребной тяги и попробуем определить, какой его точке соответствует найденная нами экономическая скорость Vэк. Мы обнаружим, что если бы мы стали постепенно уменьшать режим двигателя (дросселируя его РУДом), кривая располагаемой тяги Pp начала бы смещаться вниз параллельно самой себе. Обратите внимание на верхнюю синюю линию: эта кривая имеет не одну, а две точки пересечения с кривой потребных тяг Pп. То есть, в определенном диапазоне существуют две разные скорости (и соответствующие им два разных угла атаки), полет на которых возможен на одном и том же режиме двигателя. К этому наблюдению мы вернемся ниже, а пока продолжим уменьшать режим, пока в один прекрасный момент кривые не пересекутся в одной, самой последней точке (нижняя синяя линия). Что это за точка?

В это сложно поверить, но факт: именно эта точка и будет соответствовать экономической скорости Vэк, найденной нами ранее на графике потребных мощностей. Это неудивительно, ведь экономическая скорость — это такая скорость, горизонтальный полет на которой возможен при минимальной мощности, а значит, и РЕЖИМЕ ДВИГАТЕЛЯ. Если бы мы еще немного прибрали режим, то неизбежно начали бы снижаться. Причем изменение угла атаки в любую сторону только ускорило бы это снижение, поскольку горизонтальный полет на минимальной мощности (режиме) возможен только на экономическом угле атаки.

ГРАНИЦА ПЕРВЫХ И ВТОРЫХ РЕЖИМОВ ПОЛЕТА

Диапазон скоростей, лежащих правее Vэк., в российской школе принято называть диапазоном «первых режимов» (а в западной – front side of power curve). В этом диапазоне для увеличения скорости полета необходима бОльшая мощность (режим двигателя), для уменьшения – меньшая. Все просто и логично. Иногда подчеркивается, что в диапазоне первых режимов высота полета выдерживается штурвалом, а скорость – режимом двигателя. Именно этот диапазон скоростей используется на протяжении почти всего полета, за исключением момента выдерживания и посадки, а также для некоторых прикладных задач и тренировочных упражнений.

Как нетрудно догадаться, все, что находится левее экономической скорости Vэк, называется диапазоном «вторых режимов» (или back side of power curve). В этом диапазоне действует обратное правило: при УМЕНЬШЕНИИ скорости полета требуется БОЛЬШАЯ мощность (режим). Также, в отличие от полета на первых режимах, здесь летчик управляет воздушной скоростью изменением угла атаки (т.е. действует штурвалом), а для выдерживания высоты увеличивает (или уменьшает) режим двигателя. Именно так выполняется тренировочное упражнение «полет на малой скорости» (Slow flight).

На приведенных мной графиках (Рис. 4) диапазон вторых режимов выделен серым фоном.

Подведем промежуточные итоги для горизонтального полета:

Vэк = Speed for Maximum Endurance

Vнв = Speed for Maximum Range

Теперь можно перейти к рассмотрению набора высоты и связанных с ним скоростей Vx и Vy.

В западной школе существует устойчивая традиция обозначать рекомендованные воздушные скорости и летные ограничения самолета буквой V с буквенным индексом или цифрой. Существует целое семейство так называемых V-Speeds, среди которых Vx, Vy, Vs, Va, Vne, Vfe, Vbg, Vr, Vmc и многие другие. Полный их список вы найдете здесь.

Нас сейчас интересуют две из них: Vx и Vy. Попытаемся понять, что это за скорости, когда они используются и как соотносятся со скоростями, рассмотренными выше.

Vx – это так называемая Best Angle of Climb Speed (BAOC), «the speed at which the airplane climbs most steeply, gaining the most altitude for distance covered over the ground». From the Ground Up. Ottawa: Aviation Publishers Co. Limited; 2000, стр. 276. ISBN 0-9680390-5-7).

Как следует из английского названия и определения, эта скорость обеспечивает максимальный УГОЛ НАБОРА высоты и позволяет получить максимальную высоту за единицу РАССТОЯНИЯ. Поэтому эта скорость используется при наличии препятствий по курсу взлета, которые нужно перелететь.

В этой статье Википедии вы прочтете, что Vx «is the speed at which the maximum excess thrust is available». То есть это скорость, при которой у самолета имеется максимальный ИЗБЫТОК ТЯГИ. Чему же равна эта скорость?

Обратимся к российскому учебнику и прочитаем: “Наибольший угол подъема будет при максимальном избытке тяги. Последний для винтовых самолетов соответствует скорости, близкой к экономической». ». (Жабров А.А. Теория полета и пилотирования самолета. — М.: ДОСААФ, 1959. — С. 150.).

Бинго. Мы только что выяснили, что Vx ≈ Vэк!

Сможете угадать, чему будет соответствовать Vy? Уверен, что да.

Vу – это так называемая Best Rate of Climb Speed (ROC), «the speed at which the airplane will gain the most altitude in the least time». (From the Ground Up. Ottawa: Aviation Publishers Co. Limited; 2000, стр. 276. ISBN 0-9680390-5-7).

Из названия и определения следует, что эта скорость обеспечивает максимальную СКОРОСТЬ НАБОРА высоты (т.е. вертикальную скорость) и позволяет получить максимальную высоту за единицу ВРЕМЕНИ.

По-русски Vy называется «Наивыгоднейшая скорость набора».

Именно эта скорость используется при обычном взлете, ведь чем быстрее самолет отходит от земли, тем он безопаснее (больше возможностей для маневра в случае отказа двигателя). Кроме того, набирая скорость на Vy, самолет самым оптимальным образом использует полетное время и запас топлива, имея более высокую, по сравнению с набором на Vx, путевую скорость.

Заметим, что при необходимости выполнить взлет на Vx, после преодоления препятствий сразу же переходят к набору на Vy. Помимо прочего, эта скорость обеспечивает лучший обзор и охлаждение двигателя.

Vy (или ROC) соответствует скорости, при которой «the difference between engine power and the power required is the greatest (maximum excess power)» (Википедия). То есть это скорость, на которой самолет обладает максимальным ИЗБЫТКОМ МОЩНОСТИ.

Опять обратимся к российскому учебнику и прочтем, что, действительно, «максимальная вертикальная скорость будет при максимальном избытке мощности». А «максимальной избыток мощности получается приблизительно на наивыгоднейшей скорости». (Жабров А.А. Теория полета и пилотирования самолета. — М.: ДОСААФ, 1959. — С. 152.).

Следовательно, Vy ≈ Vнв.

Здесь, также как и в предыдущих случаях, определение предполагает некоторую неточность («приблизительно»). Это обусловлено тем, что мир несовершенен и создание идеального пропеллера и силовой установки технически невозможно. Тем не менее, скорости эти достаточно близки, чтобы считать их равными для практического применения на практике, что все и делают.

Вот мы и установили тождественность шести скоростей, используемых в горизонтальном полете и наборе высоты:

Vэк = Vx = Speed for Maximum Endurance

Vнв = Vy= Speed for Maximum Range

Займемся теперь снижением самолета. Удивительно, но здесь нам опять предстоит встреча двумя скоростями. Это какое-то колдовство, не иначе. 🙂

СКОРОСТЬ МАКСИМАЛЬНОЙ ДАЛЬНОСТИ ПЛАНИРОВАНИЯ (Best Glide Speed или Vbg)

Максимальная дальность планирования самолета (т.е. снижения с минимальной или отсутствующей тягой двигателя) будет достигнута при минимальном угле наклона траектории полета к горизонту. Взгляните на Рис. 5:

Рис. 5: Снижение самолета

Очевидно, что чем меньше угол Θ, тем дальше спланирует самолет с определенной высоты. От чего зависит этот угол? Только от качества самолета K, которое, как мы знаем, является максимальным при полете на наивыгоднейшем угле атаки. « минимальный угол планирования получим при максимальном качестве (т.е. при наивыгоднейшем угле атаки)». (Жабров А.А. Теория полета и пилотирования самолета. — М.: ДОСААФ, 1959. — С. 166.)

Выше уже говорилось о том, что наивыгоднейшему углу атаки соответствует наивыгоднейшая скорость Vнв. Поскольку это справедливо для всех режимов полета, то:

Best Glide Speed (Vbg) = Vнв

ПЕРВЫЕ И ВТОРЫЕ РЕЖИМЫ ПЛАНИРОВАНИЯ

Интересно, что «границей между первыми и вторыми режимами является планирование на наивыгоднейшем угле атаки (т. е. режим наиболее пологого планирования)». (Жабров А.А. Теория полета и пилотирования самолета. — М.: ДОСААФ, 1959. — С. 171.) Мы помним, что наивыгоднейший угол атаки соответствует Vнв, значит именно Vнв является границей первых и вторых режимов планирования. Заметьте, что если для горизонтального полета и набора высоты границей режимов является Vэк, то для для планирования — Vнв. Лучше это запомнить.

Поведение самолета на вторых режимах при планирования имеет те же особенности: ухудшение устойчивости и управляемости, а также «обратная управляемость», когда при увеличении угла атаки скорость снижения не уменьшается, а увеличивается и самолет начинает «проседать». При достижении критического угла атаки это явление еще более усиливается и называется «парашютированием». По сути, это сваливание (Stall), при котором летчик, сильно выбрав штурвал на себя, искусственно удерживает самолет на закритическом угле атаки. Самолет, летящий на таком режиме крайне неустойчив, т.к. стремиться завалиться на крыло с последующим входом в спираль или штопорное вращение. Поэтому планирование на вторых режимах допускается выполнять только на безопасной высоте.

МИНИМАЛЬНАЯ СКОРОСТЬ СНИЖЕНИЯ

Нам остается разобраться с еще одной скоростью, но зато с такой, вокруг которой образовалась некоторая понятийная чехарда. Начнем с того, что вертикальную скорость самолета в российской аэродинамике принято обозначать как Vy («скорость по вертикальной оси Y»). Это обозначение внешне совпадает, но по смыслу не имеет ничего общего с принятым в западной школе Vy (для Maximum Rate Of Climb Speed), которое мы обсуждали выше. Так что всегда, когда речь идет о Vy, следует обращать внимание на контекст. В данном случае мы говорим о вертикальной скорости при планировании или «скорости снижения» самолета.

ВОЗДУШНАЯ СКОРОСТЬ ПРИ МИНИМАЛЬНОЙ СКОРОСТИ СНИЖЕНИЯ (Minimum Rate of Descend Speed)

Планируя, самолет преодолевает сопротивление воздуха, т. е. совершает работу за счет накопленной потенциальной энергии. Выполняемая работа равна произведению его веса на высоту, которую он теряет в единицу времени. При минимальной скорости снижения эта работа будет минимальна, следовательно, на ее выполнение будет расходоваться минимальная мощность, а это имеет место лишь при полете на экономическом угле атаки и Vэк. «Итак, минимальную вертикальную скорость планирования получим, планируя с экономической скоростью горизонтального полета». (Жабров А.А. Теория полета и пилотирования самолета. — М.: ДОСААФ, 1959. — С. 169.)

Таким образом, мы выяснили, что:

Minimum Rate of Descend Speed = Vэк

Vэк = Vx = Speed for Maximum Endurance = Speed for Minimum Rate of Descend

Vнв = Vy= Speed for Maximum Range = Best Glide Speed (Vbg)

Ну, а кто не верит в это и хочет выловить таинственного «мэджика» самостоятельно – район поисков я обозначил! 🙂

Видео:Мгновенная скорость (видео 6)| Векторы. Прямолинейное движение | ФизикаСкачать

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Видео:Вектор скорости и траекторияСкачать

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Видео:Мгновенная скорость (видео 6) | Векторы. Прямолинейное движение | ФизикаСкачать

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Видео:Как найти проекцию вектора скорости и ускорения. Выполнялка 112Скачать

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Видео:Урок 9. Проекции вектора на координатные осиСкачать

Движение тела, брошенного под углом к горизонту

теория по физике 🧲 кинематика

Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.

Важные факты! График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело

1. Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
2. Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v_0x = v₀cosα. Ее проекция на ось ОУ равна v_0y = v₀sinα.
3. Проекция мгновенной скорости на ось ОХ равна: v_x = v₀ cosα. Ее проекция на ось ОУ равна нулю: v_y = v₀ sinα – gt.
4. Проекция ускорения свободного падения на ось ОХ равна нулю: g_x = 0. Ее проекция на ось ОУ равна –g: g_y = –g.

Видео:Физика 13. Формула расчёта скорости. Определение вектора скорости — Академия занимательных наукСкачать

Кинематические характеристики

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:

Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:

Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: v_y = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v₀ cosα, данная формула принимает вид:

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v₀ sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?

Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:

Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Видео:1.6. Вектор скорости материальной точки. ЕГЭ по физике.Скачать

Тело, брошенное под углом к горизонту с некоторой высоты

Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.

График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: t_пад > t_под.

Полное время полета равно:

Уравнение координаты x:

Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.

Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:

x = v₀ cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.

Алгоритм решения

Решение

Запишем исходные данные:

Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.

Закон сохранения энергии:

Потенциальная энергия шарика в точке А равна:

Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.

В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:

Перед ударом кинетическая энергия шарика равна:

Согласно закону сохранения энергии:

E p A = E p B + E k B

m g H = m g l 1 + m v 2 2 . .

Отсюда высота H равна:

H = m g l 1 m g . . + m v 2 2 m g . . = l 1 + v 2 2 g . .

Относительно точки В шарик поднимется на высоту h – l₁. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:

h − l 1 = v 2 sin 2 . β 2 g . . = v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

l 1 = h − v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:

H = l 1 + v 2 2 g . . = h − ( g t ) 2 sin 2 . ( 90 − 2 α ) o 2 g . . + ( g t ) 2 2 g . .

H = h − g t 2 sin 2 . ( 90 − 2 α ) 2 . . + g t 2 2 . . = h − g t 2 2 . . ( sin 2 . ( 90 − 2 α ) o − 1 )

H = 1 , 4 − 10 · 0 , 4 2 2 . . ( sin 2 . ( 90 − 6 0 ) o − 1 )

H = 1 , 4 − 5 · 0 , 16 ( sin 2 . 3 0 o − 1 )

H = 1 , 4 − 0 , 8 ( ( 1 2 . . ) 2 − 1 ) = 1 , 4 − 0 , 8 ( 1 4 . . − 1 )

H = 1 , 4 + 0 , 6 = 2 ( м )

pазбирался: Алиса Никитина | обсудить разбор | оценить

В момент t=0 мячик бросают с начальной скоростью v₀ под углом α к горизонту с балкона высотой h (см. рисунок).

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).

К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Решение

Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.

Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.

Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.

Формула проекции скорости мячика на ось ОХ:

Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.

Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.

Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.

Теперь записываем установленные соответствия в порядке АБ: 42.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

1. увеличивается
2. уменьшается
3. не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1. Сделать чертеж, иллюстрирующий ситуацию.
2. Записать формулы, определяющие указанные в условии задачи величины.
3. Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.

Решение

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

pазбирался: Алиса Никитина | обсудить разбор | оценить

🌟 Видео

Урок 12. Равномерное прямолинейное движениеСкачать

Перемещение и скорость как векторыСкачать

Урок 15 (осн). Механическое движение. СкоростьСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Урок 17. Средняя скорость. Средняя путевая скорость.Скачать

Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

Лекция 3.4 | Перемещение и скорость материальной точки | Александр Чирцов | ЛекториумСкачать

Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать