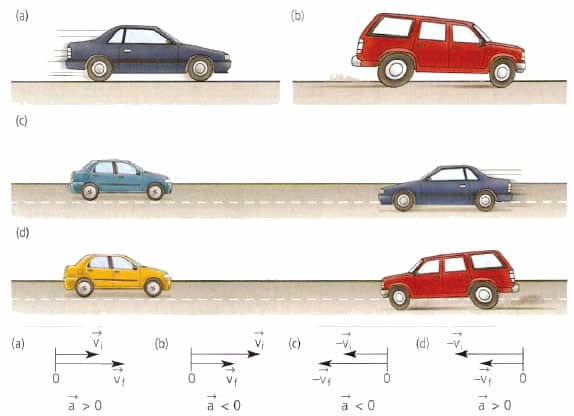
Как известно, любая физическая величина относится к одному из двух типов, она является либо скалярной, либо векторной. В данной статье рассмотрим такие кинематические характеристики как скорость и ускорение, а также покажем, куда направлены векторы ускорения и скорости.
Видео:Физика | Ликбез по векторамСкачать

Что такое скорость и ускорение?
Обе величины, названные в этом пункте, являются важными характеристиками любого вида движения, будь то перемещение тела по прямой линии или по криволинейной траектории.

Скоростью называется быстрота изменения координат во времени. Математически эта величина равна производной по времени пройденного пути, то есть:
Здесь вектор l¯ направлен от начальной точки пути к конечной.
В свою очередь ускорение – это скорость, с которой изменяется во времени сама скорость. В виде формулы оно может быть записано так:
Очевидно, что взяв вторую производную от вектора перемещения l¯ по времени, мы также получим значение ускорения.
Поскольку скорость измеряется в метрах в секунду, то ускорение, согласно записанному выражению, измеряется в метрах в секунду в квадрате.
Видео:На рисунке изображены вектор скорости v движущегося тела и вектор силы F, действующей на - №27906Скачать

Куда направлены векторы ускорения и скорости?
В физике всякое механическое движение тела принято характеризовать определенной траекторией. Последняя представляет собой некоторую воображаемую кривую, вдоль которой тело перемещается в пространстве. Например, прямая линия или окружность — это яркие примеры распространенных траекторий движения.
Вектор скорости тела направлен в сторону движения всегда, независимо от того, замедляется или ускоряется тело, движется оно по прямой или по кривой. Если говорить геометрическими терминами, то вектор скорости направлен по касательной к точке траектории, в которой в данный момент находится тело.
Вектор ускорения точки материальной или тела не имеет ничего общего со скоростью. Этот вектор направлен в сторону изменения скорости. Например, для прямолинейного движения величина a¯ может как совпадать по направлению с v¯, так и быть противоположной v¯.
Видео:Физика: Понятие Вектор, Вектор СкоростиСкачать

Действующая на тело сила и ускорение
Мы выяснили, что вектор ускорения тела направлен в сторону изменения вектора скорости. Тем не менее не всегда можно легко определить, как меняется скорость в данной точке траектории. Более того, для определения изменения скорости необходимо выполнить операцию разности векторов. Чтобы избежать этих трудностей в определении направления вектора a¯, существует еще один способ быстро его узнать.
Ниже записан знаменитый и хорошо известный каждому школьнику закон Ньютона:
Формула показывает, что причиной возникновения ускорения у тел является действующая на них сила. Поскольку масса m является скаляром, то вектор силы F¯ и вектор ускорения a¯ направлены одинаково. Этот факт следует запомнить и применять на практике всегда, когда возникает необходимость в определении направления величины a¯.
Если на тело действуют несколько разных сил, тогда направление вектора ускорения будет равно результирующему вектору всех сил.
Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Движение по окружности и ускорение
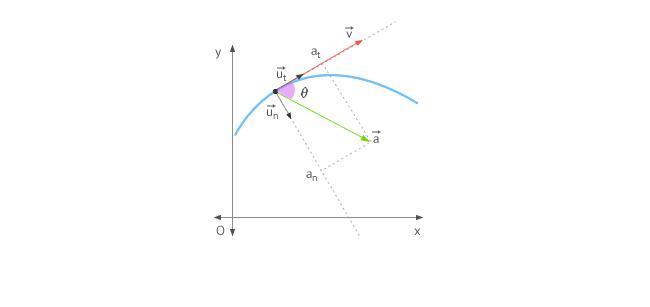
Когда тело перемещается по прямой линии, то ускорение направлено либо вперед, либо назад. В случае же движения по окружности ситуация усложняется тем, что вектор скорости постоянно меняет свое направление. В виду сказанного, полное ускорение определяется двумя его составляющими: тангенциальным и нормальным ускорениями.
Тангенциальное ускорение направлено точно так же, как вектор скорости, или против него. Иными словами, эта компонента ускорения направлена вдоль касательной к траектории. Ускорение тангенциальное описывает изменение модуля самой скорости.
Ускорение нормальное направлено вдоль нормали к данной точке траектории с учетом ее кривизны. В случае движения по окружности вектор этой компоненты указывает на центр, то есть нормальное ускорение направлено вдоль радиуса вращения. Эту компоненту часто называют центростремительной.
Полное ускорение представляет собой сумму названных компонент, поэтому его вектор может быть направлен произвольным образом по отношению к линии окружности.
Если тело совершает вращение без изменения линейной скорости, то существует отличная от нуля только нормальная компонента, поэтому вектор полного ускорения направлен к центру окружности. Заметим, что к этому центру также действует сила, удерживающая тело на его траектории. Например, сила гравитации Солнца удерживает нашу Землю и другие планеты на своих орбитах.
Видео:Урок 9. Проекции вектора на координатные осиСкачать

Импульс в физике
Любое тело, обладающее скоростью, обладает импульсом.
Тело всегда движется туда, куда направлен вектор его скорости.
Импульс тела – это вектор. Он сонаправлен с вектором скорости тела.
Покоящееся тело импульса не имеет — если тело не движется, его импульс равен нулю.
Физики различают два вектора – импульс тела и импульс силы.
Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Импульса тела, формула
Возьмем вектор ( vec ) скорости тела (рис. 1), умножим его на ( m ) массу тела (масса — скаляр), получим новый вектор, обозначим его ( p ). Длина этого вектора отличается от длины скорости, а направление – совпадает.
Подробнее о умножении вектора на число написано тут.
[ large boxed < veccdot m = vec
>]
( vec left( frac< text> right) ) – скорость тела, вектор
( m left( text right) ) – масса тела, скаляр (просто число)
( vec
left( text cdot frac< text> right) ) – импульс тела, вектор, он сонаправлен со скоростью тела
Если тело не движется, оно импульсом не обладает ( vec
= 0 ).
Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Импульс силы, формула
На тело может действовать сила, например, когда тело соударяется с каким-то другим телом. Тела взаимодействуют с помощью сил. Что такое сила, написано тут.
Действие происходит не мгновенно, а в течение какого-то промежутка времени.
Возьмем вектор ( vec ) силы, действующей на тело (рис. 2), умножим его на ( Delta t ) кусочек времени, в течение которого сила действовала (время — скаляр), получим новый вектор. Для этого вектора не придумали специального обозначения.
( vec left( H right) ) – сила, действующая на тело, вектор
( Delta t left( c right) ) – время воздействия силы (просто число). Можно пояснить так:
Пусть сила действовала несколько секунд. Тогда ( Delta t = t — t_ ) – разница между двумя положениями секундной стрелки на часах.
- ( t left( c right) ) – конечное положение стрелки,
- ( t_ left( c right) ) – начальное положение стрелки.
Длины векторов силы и импульса силы отличаются, а направления – совпадают.
Если сила не действует ( vec = 0 ), то вектор импульса силы отсутствует ( vec cdot Delta t = 0 ).
Импульс тела и импульс силы связаны. В этой статье подробно описана связь между этими векторами.
Видео:Вектор скорости и траекторияСкачать

Вектор силы и вектор скорости
Простейшие примеры векторов в физике — скорость и сила.
1. Всякое движение можно представить как результат сложения нескольких движений, его составляющих. Скорость результирующего движения изображается по величине и направлению диагональю параллелограмма, построенного на отрезках, изображающих составляющие скорости, как на сторонах. Рассмотрим конкретный пример.
Рыбак переправляется на лодке `A` через реку, которая течёт в сторону, указанную стрелкой (рис. 18). Пусть скорость течения воды `vec(v_1)` изображается по величине и направлению отрезком `AB`, а скорость `vec(v_2)` движения лодки относительно воды под влиянием усилий гребца изображается отрезком `AC` (в стоячей воде лодка двигалась бы по направлению `AC` со скоростью `vec(v_2)`). Лодка будет двигаться относительно берега по направлению `AM` со скоростью `vec v`, изображаемой диагональю `AD` параллелограмма, построенного на векторах `vec(v_1)` и `vec(v_2)` (в данном случае параллелограмм `ABCD` является прямоугольником).
2. Сила — как векторная величина — всегда имеет определённое направление, модуль, а также точку приложения.
Часто встречаются случаи, когда на тело действуют несколько сил. Тогда бывает удобно заменить их одной силой, которая производит на тело такое же действие, как и несколько одновременно действующих сил. Такую силу (если она существует) называют равнодействующей. Нахождение равнодействующей нескольких сил осуществляется с помощью правил векторного сложения, при этом слагаемые силы называют составляющими.
Так, несколько сил, действующих на одну и ту же точку тела, всегда можно заменить одной равнодействующей, как бы ни были направлены силы и каковы бы ни были их величины. Пусть, например, на тело действуют четыре силы `vec(F_1)`, `vec(F_2)`, `vec(F_3)` и `vec(F_4)`, приложенные к одной точке `O` и лежащие в одной плоскости (рис. 19). Тогда их равнодействующая `vec F` будет равна векторной сумме этих сил, найденной по правилу многоугольника (рис. 20).
Найти равнодействующую `vec R` трёх равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми силами равны между собой.
`F_1 = F_2 = F_3 = F`.
См. рис. 21. Углы между парами векто ров `vec(F_1)` и `vec(F_2)`, `vec(F_2)` и `vec(F_3)`, а также между векторами `vec(F_1)` и `vec(F_3)`, равны друг другу и равны `120^@` . Сложим силы `vec(F_2)` и `vec(F_3)` по правилу параллелограмма. Вследствие равенства модулей сил `vec(F_2)` и `vec(F_3)` этот параллелограмм есть ромб. Сумма сил `vec(F_2) + vec(F_3)` есть диагональ ромба, поэтому углы между парами векторов `vec(F_2)` и `vec(F_2) + vec(F_3)`, а также `vec(F_3)` и `vec(F_2) + vec(F_3)` равны по `60^@` , т. е. векторы `vec(F_1)` и `vec(F_2) + vec(F_3)` направлены вдоль одной прямой, но в противоположные стороны. Силовой параллелограмм, построенный на векторах `vec(F_2)` и `vec(F_3)`, состоит из двух равносторонних треугольников, поэтому модуль силы
`|vec(F_2) + vec(F_3)| = F_2 = F_3 = F = F_1`, т. е `vec F_1 = — (vec(F_2) + vec(F_3))`,
откуда следует `vec(F_1) + vec(F_2) + vec(F_3) = 0`.
К телу приложено `6` сил, лежащих в одной плоскости и составляющих друг с другом углы в `60^@`. Силы последовательно равны `1`, `2`, `3`, `4`, `5` и `6 Н`. Найти равнодействующую `vec R` этих шести сил.
Сложение сил по правилу многоугольника здесь нецелесообразно. Поступим иначе. Сложим сначала попарно силы, направленные вдоль одной прямой (см. рис. 22 а, б, в).
`|vec(F_2) + vec(F_4)| = 4 — 1 = 3`,
аналогично `|vec(F_2) + vec(F_5)| = 5 — 2 = 3` и `|vec(F_3) + vec(F_6)| = 6 — 3 = 3`.
Сумма сил `vec(F_2) + vec(F_5)` направлена вдоль вектора `vec(F_5)`. Туда же направлена и сумма сил `vec(F_1) + vec(F_4) + vec(F_3) + vec(F_6)`, причём модуль этой силы равен `3`. В итоге получаем, что сумма всех шести сил `vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)` направлена вдоль направления силы `vec(F_5)`, а модуль этой силы `|vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)| = 3 + 3 = 6 Н`.
Найти равнодействующую `vec R` пяти равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми соседними силами равны между собой (см. рис. 23). (Эти углы, разумеется, равны `360^@ //5 = 72^@`.)
В отличие от предыдущего примера здесь мы имеем нечётное число сил, поэтому невозможно образовать из них целое число пар. Поступим иначе. Возьмём какую-нибудь силу, например, `vec(F_1)`, а остальные сгруппируем в пары и попарно сложим их (см. рис. 24):
`vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`.
Почему удобна именно такая группировка сил в пары? Дело в том, что обе суммы сил (и `vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`) направлены вдоль линии действия силы `vec(F_1)`. Ясно, что равнодействующая всех сил будет направлена вдоль линии действия силы `vec(F_1)`. Модули сумм сил легко найти из геометрии. Например, в силовом параллелограмме, построенном на векторах `vec(F_2)` и `vec(F_5)`, который является ромбом, длина диагонали ромба (модуль силы `vec(F_2) + vec(F_5)`) равна удвоенной половинке диагонали, а та легко ищется из любого из четырёх прямоугольных треугольников, на которые ромб разбивается диагоналями. В результате
`|vec(F_2) + vec(F_5) | = 2F cos 72^@`,
где `F` — модуль любой из пяти исходных сил. Аналогично
`|vec(F_3) + vec(F_4)| = 2F cos 36^@`.
В итоге для модуля искомой силы получаем формулу
`R = F(1 + 2 cos 72^@ — 2 cos 36^@)` (*).
Для углов `72^@` и `36^@` нет таких простых формул, как для углов `30^@`, `45^@` или `60^@`. Пользуясь калькулятором, можно, однако, показать, что согласно формуле (*) `R = 0`.
Имеется и более красивое доказательство того, что результирующий вектор есть нулевой вектор. В самом деле, мы довольно произвольно взяли в качестве силы, которой не хватило пары, силу `vec(F_1)`. Если бы в качестве такой взять силу `vec(F_2)`, а в пары объединить `vec(F_1)` и `vec(F_3)` (одна пара) и `vec(F_4)` и `vec(F_5)`, то, повторив рассуждения, получим, что равнодействующая всех пяти сил `vec R` должна быть направлена вдоль линии действия силы `vec(F_2)`. Возможно ли, чтобы вектор был одновременно направлен вдоль двух несовпадающих друг с другом направлений (и `vec(F_1)`, и `vec(F_2)`; а на самом деле, как догадался читатель, ещё и вдоль направления действия сил `vec(F_3)`, `vec(F_4)` и `vec(F_5)`!)? Ненулевым вектор не может быть! Остаётся одна возможность: суммарный вектор – нулевой!
В примерах 10 и 11 мы искали по правилу параллелограмма суммы сил.
В примере 12 нас интересовала лишь проекция равнодействующей силы на направление (например, силы `vec(F_1)`).
В следующих примерах наш интерес будет также скорее не к равнодействующей силе, а только к каким-то её проекциям.
Электрический фонарь весом `Q = 16 Н` укреплён, как показано на рис. 25.
Определите отношение натяжений `T_1` и `T_2` в проволоках `BA` и `BC`, углы наклона которых даны на рисунке.
В условиях равновесия сумма всех сил, приложенных к точке `B`, равна нулю. Поэтому проекция равнодействующей всех сил на горизонтальное направление тоже равна нулю. Проекция силы со стороны проволоки, идущей к фонарю, на это направление равна нулю (эта сила вертикальна). Остаются вклады от двух натяжений со стороны проволок `BA` и `BC`. Горизонтальную ось направим слева направо. Тогда имеем: T 1 , гор + T 2 , гор = 0 T_<1,;mathrm>+T_<2,;mathrm>=0 (см. рис. 26), т. е.
`T_1 * cos 60^@ — T_2 cos 45^@ = 0`
(или `T_1 * sin 30^@ — T_2 sin 45^@ = 0`), откуда получаем `T_1//T_2 = sqrt2`.
Однородная массивная верёвка подвешена за два конца на разных высотах (см. рис. 27). Масса верёвки `m`. Углы, которые составляет верёвка с вертикалью в точках закрепления, равны `30^@` и `60^@`.
Определите силы натяжения верёвки вблизи её точек крепления.
Задача кажется очень трудной, т. к. не ясно, какую роль играет неизвестная нам форма верёвки, которую она примет под действием сил тяжести всех частей верёвки. (В предыдущем примере мы не интересовались провисанием проволок под действием силы тяжести, молчаливо считая провисание малым.) И всё же задача в той постановке, в какой дана, имеет простое решение. Мысленно проведём горизонтальную ось слева направо. Поскольку верёвка находится в равновесии, то сумма проекций всех сил на горизонтальное направление равна нулю. Сила тяжести верёвки имеет нулевую проекцию на это направление (эта сила направлена вертикально). Снова остаются вклады от двух натяжений (см. рис. 28):
Полагая `sin 30^@ = 1//2` и `sin 60^@ = sqrt3 //2`, находим `T_1 // T_2 = sqrt3`. Мысленно проведём ещё и вертикальную ось, направив её вниз. Сумма проекций всех сил на эту ось также равна нулю:
`mg — T_1 cos 30^@ — T_2 cos 60^@ = 0`.
Учитывая найденное ранее соотношение между `T_1` и `T_2` и значения `cos 60^@ = 1//2` и `cos 30^@ = sqrt3 //2`, получаем:
`mg — sqrt3 * T_2 * sqrt3 //2 — T_2 //2 = 0`,
`T_2 = mg//2` и `T_1 = sqrt3 mg//2`.
На гладкой наклонной плоскости с углом наклона `alpha` лежит брусок массой `m`. Какую горизонтальную силу нужно приложить к бруску, чтобы он находился в покое (рис. 29)?
Определите также модуль нормальной силы реакции на брусок со стороны наклонной плоскости.
Брусок по условию задачи покоится. Значит, сумма всех сил, приложенных к бруску, равна нулю. Равны нулю и суммы проекций сил на любые направления, в частности, на направление вдоль наклонной плоскости и перпендикулярное ему. Нормальная сила реакции `vec N` со стороны наклонной плоскости имеет равную нулю составляющую вдоль наклонной плоскости.
Проекция сила тяжести `m vec g` на ось `Ox` вдоль наклонной плоскости (рис. 30) равна `- mg sin alpha`, а проекция горизонтальной силы `F` на эту ось равна `F cos alpha`. Других сил вдоль наклонной плоскости не действует (плоскость, по условию задачи, гладкая, т. е. сила трения пренебрежимо мала). Приравнивая нулю сумму проекций на ось `Ox` всех сил, действующих на тело, получаем: `- mg sin alpha + F cos alpha = 0`, откуда находим
`F = mg (sin alpha)/(cos alpha) = mg * bbb»tg» alpha`.
Для отыскания `N` обратимся к проекциям сил на направление `Oy`. Приравняем нулю и сумму проекций на ось `Oy`:
`N — mg cos alpha — F sin alpha = 0`,
откуда `N = mg cos alpha + F sin alpha`, или с учётом найденного значения `F`:
`N = mg cos alpha + mg (sin^2 alpha)/(cos alpha) = mg (cos^2 alpha + sin^2 alpha)/(cos alpha)`,
тогда с учётом основного тригонометрического тождества, `sin^2 alpha + cos^2 alpha = 1`, получаем окончательно
На шероховатой поверхности доски лежит брусок массой `m`. К нему приложена сила, направленная под углом `alpha` к горизонту (см. рис. 31).
Определите модуль нормальной силы реакции со стороны поверхности.
Поскольку брусок не проваливается и не подскакивает вверх, то сумма проекций сил на вертикальную ось равна нулю:
`N + F * sin alpha — mg = 0`,
(см. рис. 32), откуда находим
`N = mg — F * sin alpha`.
Часто совершенно безосновательно приравнивают силу реакции `N` силе тяжести `mg`. Мы видим, что даже в случае горизонтальной поверхности это в общем случае не так. Для наклонной плоскости это тоже не так. В предыдущем примере нормальная сила реакции равнялась `mg//cos alpha`. Кстати, если бы удерживающая сила `F` действовала там не вдоль горизонтали, а вдоль наклонной плоскости, то для удержания бруска на наклонной плоскости потребовалась бы сила величиной `F = mg sin alpha`, а нормальная сила реакции была бы равна `N = mg cos alpha` (и снова не равнялась бы `mg`!)
Докажите это самостоятельно.
(См. рис. 33). В данном примере мы имеем дело с весьма простым случаем разложения скорости на два взаимно перпендикулярных направления:
`vec v = vec(v _sf»гор») + vec(v_sf»верт»)`,
(См. рис. 34). В данном случае мы имеем дело со сложением движений: `vec(v_sf»с») = vec(v_sf»св») + vec(v_sf»в»)`, где `vec(v_sf»св»)` — скорость самолёта относительно воздуха (модуль которой равен скорости самолёта относительно земли в безветренную погоду), а `vec(v_sf»в»)` — скорость воздуха. Далее по теореме Пифагора получаем:
Как и в примере 9, мы также имеем дело со случаем сложения движений. Но там было проще: не требовалось выбирать никакой стратегии, рыбак лишь наблюдал, как снесёт его лодку течением воды в реке. Если бы вода в реке покоилась, то, направив корпус лодки под углом `alpha` к нормали, мы заставили бы её двигаться в направлении вектора `vec V` (см. рис. 35). В действительности, вода в реке не стоячая, а имеет скорость `vec u` Поэтому сносимая течением лодка будет двигаться в направлении вектора `vec v` таком, что `vec v = vec V + vec u`. Учитывая, что оба треугольника в параллелограмме на рис. 35 прямоугольные (по условию, лодка должна двигаться перпендикулярно берегам), находим
`sin alpha = u//V = 3//5`, `alpha
а по теореме Пифагора v = V 2 — u 2 = 4 м / с v=sqrt=4;mathrm м/mathrm с .
В данном примере скорость лодки относительно воды меньше, чем скорость воды в реке, `V *
Лодку вытягивают из воды, стоя на крутом берегу и выбирая верёвку, которая привязана к носу лодки, со скоростью `v` (см. рис. 37).
Какой будет скорость лодки `u` в момент, когда верёвка будет составлять угол `alpha` с горизонтом? Верёвка нерастяжима.
Традиционная ошибка решающих эту задачу состоит в том, что пытаются разложить движение лодки на два направления – горизонтальное и вертикальное, делая (неправильное!) построение, как показано на рис. 38а и получая неверный ответ `u = v * cos alpha`. Что здесь неправильно? В отличие от самолёта из примера 17, который двигался под отличным от нуля углом к горизонту (см. рис. 33), здесь лодка движется горизонтально ! Сделаем другое разложение скорости лодки `vec u` по двум направлениям – вдоль верёвки (в данный момент времени!) и перпендикулярно ей (см. рис. 38б).
Проекция вектора `vec u` на направление верёвки будет равна скорости `v`, с которой выбирают верёвку: `v = u cos alpha`, поэтому `u = v/(cos alpha)`.
Поясним ещё, почему проекция вектора `vec u` на направление верёвки будет равна скорости `v` с которой выбирают верёвку. Если мы имеем абсолютно твердое тело (АТТ), деформациями в котором можно пренебречь, или нерастяжимую нить (но уже максимально натянутую), то как бы ни двигались АТТ или нерастяжимая нить, они будут обладать следующим свойством. Возьмём две произвольные точки `A` и `B` нити или АТТ и мысленно соединим их прямой. Тогда составляющие скоростей выбранных точек вдоль этой прямой в любой момент времени будут равны друг другу: v A ∥ → = v B ∥ → overrightarrow<v_>=overrightarrow<v_> (см. рис. 39). В противном случае изменялось бы расстояние между точками `A` и `B`. Составляющие скорости, перпендикулярные отрезку прямой `AB`, могут быть при этом любыми.
Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 40). В некоторый момент времени силы натяжения тросов, идущих от лодок 1 и 2, равны друг другу по модулю и равны `F`. Угол между тросами равен `2 alpha`. Какая равнодействующая сила приложена к буксируемой лодке со стороны тянущих её лодок? Чему будет равна эта сила в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?
Две силы нужно сложить по правилу параллелограмма, который в данном случае будет ещё и ромбом с перпендикулярными друг другу диагоналями, разбивающими его на четыре равных прямоугольных треугольника. Из геометрии рис. 41 видно, что модуль равнодействующей силы `R` равен удвоенной длине прилежащего катета: `R = 2F cos alpha`. При стремлении угла между направлениями тросов к нулю `R -> 2F` (`cos alpha -> 1` при `alpha -> 0`).
Хитрее оказывается похожая задача, когда заданы не силы, а скорости.
Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 42). В некоторый момент времени модули скоростей лодок 1 и 2 равны друг другу и равны `v_1 = v_2 = v`. Найти модуль и направление скорости буксируемой лодки `u`. Тросы нерастяжимы. Чему будет равна эта скорость в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?
Ясно, что «решение» `u = 2v cos alpha` (как в предыдущем примере) не подходит, т. к. при `alpha -> 0` мы получили бы, что `u -> 2v`, чего не может быть. Если, например, две собаки в упряжке бегут с одинаковыми скоростями `v` в одном направлении, то и скорость упряжки будет равна этой же скорости `v` (если, конечно, упряжка не отцепилась или к ней не подключили дополнительно мотор).
Решение задачи такое же, как в примере 21. В данном примере важнейшими словами являются «Тросы нерастяжимы». Ясно, что правильное построение, учитывающее это условие, должно быть таким, как на рис. 43, откуда немедленно получаем `v = u cos alpha`, поэтому `u = v/(cos alpha)`. Тогда в предельном случае, когда `alpha -> 0`, имеем `u -> v`, как и должно быть.
Заметим, что четырёхугольник на рис. 43 весьма мало похож на параллелограмм из предыдущего примера. Еще меньше будет похож на параллелограмм этот четырёхугольник, когда модули скоростей `v_1 != v_2` (см. рис. 44).
Две лодки буксируют третью с помощью двух тросов (рис. 45). В некоторый момент времени скорость 2-ой лодки в 2 раза больше, чем скорость 1-ой, `v_2 = 2v_1 = 2v`, а угол между тросами равен `90^@`. В каком направлении и с какой скоростью движется в этот момент буксируемая лодка? Тросы нерастяжимы.
В данном случае четырёхугольник на рис. 44 будет прямоугольником — см. рис. 46 (т. е. всё же параллелограммом).
По определению тангенса угла `»tg»varphi _1 = v_2 //v_1 = 2`, откуда, пользуясь калькулятором, находим `varphi _1
63^@`; `varphi _2 = 90^@ — varphi _1
Модуль скорости буксируемой лодки найдём по теореме Пифагора (раз уж у нас «случайно» появились прямоугольные треугольники):
`u = sqrt(v_1^2 + v_2^2) = sqrt(v^2 + (2v)^2) = sqrt5 * v
🌟 Видео
Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Урок 32 (осн). Сила. Единицы силы. Изображение силСкачать

Построение проекции вектора на осьСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Как проецировать вектор сил на оси | ЕГЭ Физика | Николай Ньютон. ТехноскулСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

Скалярные и векторные величины, основные определения.Скачать
Относительность 5 - Пространство Минковского. 4-векторы.Скачать

Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

Физика 7 класс (Урок№8 - Скорость.)Скачать