Найти минимальную площадь треугольника

треугольник считается описаным вокруг эллипса если что выполнено
эллипс касается трех сторон так?

гм наверно надо пинать тот вариант что не очень хорошо получается

Может с некоторым опозданием, но меня посетила следующая мысль.

Начало, как и говорилось выше, это замена, связанная с растяжением/сжатием по осям. при этом касательные перейдут в касательные, а площадь измениться пропорционально коэффициентам растяжения/сжатия.

И вот дальше возникшая мысль о используемых переменных задачи.
Мы имеем треугольник, в который вписана единичная окружность. Рассмотрим в качестве переменных — углы при основании.

рисунок.

Поскольку центр вписанной окружности лежит на биссектрисах, то мы легко выражаем части сторон треугольника от вершины до основания радиуса через углы. с учётом того, что радиус равен 1.
`AF = AD = ctg(phi), CF = CE = ctg(psi), BD = BE = ctg(pi/2 — phi — psi) = tg(phi + psi)`

Следовательно, `S_ = p*r = ctg(phi) + ctg(psi) + tg(phi + psi)` . и условия на углы `phi >= 0, psi >= 0, phi + psi

Ну, вот . вроде обозримая задача получилась.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Минимальная площадь многоугольника с учетом трех точек

Учитывая три точки правильного многоугольника (n> 3), найдите минимальную площадь правильного многоугольника (все стороны одинаковы), возможную с заданными точками.

Примеры:

Прежде чем мы продолжим, стоит отметить, что количество сторон должно быть не менее 4 (обратите внимание, условие n> 3).

Здесь мы должны найти минимально возможную площадь для правильного многоугольника, поэтому для вычисления минимально возможной площади нам нужно вычислить требуемое значение n. Поскольку длина стороны не указана, мы сначала вычислим окружность треугольника, образованного точками. Дается по формуле
R = abc / 4A
где a, b, c — стороны сформированного треугольника, а A — площадь поперечного сечения. Здесь площадь треугольника может быть рассчитана по формуле Герона .

После расчета окружности треугольника рассчитываем площадь многоугольника по формуле

А = пХ (син (360 / л) хт 2/2)

Здесь r представляет окружность n-гона (правильный многоугольник n сторон).
Но сначала мы должны вычислить значение n. Чтобы вычислить n, мы сначала должны вычислить все углы треугольника по формуле косинуса
cosA = (b 2 + c 2 -a 2 ) / 2bc
cosB = (a 2 + c 2 -b 2 ) / 2ac
cosC = (a 2 + b 2 -c 2 ) / 2ab

Тогда n определяется как
n = pi / GCD (A, B, C)
где A, B и C — углы треугольника. После вычисления n подставляем это значение в формулу для расчета площади многоугольника.

Ниже приведена реализация данного подхода:

// Программа CPP для поиска минимальной площади полигона
// количество сторон больше трех с заданными тремя точками.
#include

using namespace std;

// присваиваем значение pi переменной

const double pi = 3.14159265359;

// вычисление значения gcd двух двойных значений.

double gcd( double x, double y)

return fabs (y) fmod (x, y));

// Расчет минимальной площади полигона с помощью этой функции.

double min_area_of_polygon( double Ax, double Ay, double Bx,

double By, double Cx, double Cy)

double a, b, c, Radius, Angle_A, Angle_B, Angle_C,

semiperimeter, n, area;

// вычисляем длину сторон треугольника

// сформирован из заданных точек a, b, c представляет

// длина разных сторон треугольника.

a = sqrt ((Bx — Cx) * (Bx — Cx) + (By — Cy) * (By — Cy));

b = sqrt ((Ax — Cx) * (Ax — Cx) + (Ay — Cy) * (Ay — Cy));

c = sqrt ((Ax — Bx) * (Ax — Bx) + (Ay — By) * (Ay — By));

// здесь мы вычислили полупериметр треугольника.

semiperimeter = (a + b + c) / 2;

// Теперь из полупериметра получена площадь треугольника

// через формулу цапли.

double area_triangle = sqrt (semiperimeter * (semiperimeter — a)

// таким образом, окружность треугольника получается из

// стороны и площадь треугольника рассчитаны.

Radius = (a * b * c) / (4 * area_triangle);

// Теперь каждый угол треугольника получен из сторон

Angle_A = acos ((b * b + c * c — a * a) / (2 * b * c));

Angle_B = acos ((a * a + c * c — b * b) / (2 * a * c));

Angle_C = acos ((b * b + a * a — c * c) / (2 * b * a));

// Теперь n вычисляется так, чтобы площадь была минимальной для

n = pi / gcd(gcd(Angle_A, Angle_B), Angle_C);

// вычисление площади правильного н-гона через окружность

area = (n * Radius * Radius * sin ((2 * pi) / n)) / 2;

// три точки даны как входные данные.

double Ax, Ay, Bx, By, Cx, Cy;

printf ( «%.2f» , min_area_of_polygon(Ax, Ay, Bx, By, Cx, Cy));

# Python3 программа для поиска минимальной площади
# многоугольник числа сторон больше трех
# с учетом трех баллов.

# из математической библиотеки импортировать каждую функцию

from math import *

# присвоение значения pi переменной

# вычисление значения gcd двух двойных значений.

return gcd(y, fmod(x, y))

# Расчет минимальной площади полигона
# через эту функцию.

def min_area_of_polygon(Ax, Ay, Bx,

# расчет длины сторон

# треугольник, образованный из заданных точек

# a, b, c представляет длину разных

a = sqrt((Bx — Cx) * (Bx — Cx) +

b = sqrt((Ax — Cx) * (Ax — Cx) +

c = sqrt((Ax — Bx) * (Ax — Bx) +

# здесь мы рассчитали полупериметр

semiperimeter = (a + b + c) / 2

# Теперь из области полупериметра треугольника

# выводится по формуле цапли

# Таким образом, окружность треугольника выводится

# от сторон и площади треугольника рассчитывается

Radius = (a * b * c) / ( 4 * area_triangle)

# Теперь каждый угол треугольника получен

# со стороны треугольника

Angle_A = acos((b * b + c * c — a * a) / ( 2 * b * c))

Angle_B = acos((a * a + c * c — b * b) / ( 2 * a * c))

Angle_C = acos((b * b + a * a — c * c) / ( 2 * b * a))

# Теперь n рассчитывается так, что площадь

# минимум для обычного н-гона

n = pi / gcd(gcd(Angle_A, Angle_B), Angle_C)

# Расчет площади регулярного н-гона через

area = (n * Radius * Radius *

sin(( 2 * pi) / n)) / 2

if __name__ = = «__main__» :

# три очка даны в качестве входных данных.

print ( round (min_area_of_polygon(Ax, Ay, Bx,

Видео:Как найти площадь треугольника без формулы?Скачать

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Видео:Как найти площадь треугольника? #треугольник #математика #егэ #shorts #подготовкакегэ #огэ #площадьСкачать

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Видео:8 класс, 14 урок, Площадь треугольникаСкачать

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Видео:Площади треугольникаСкачать

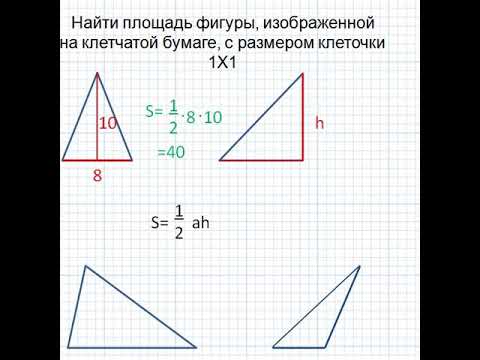
Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Видео:Найти площадь треугольника АВС. Задачи по рисункамСкачать

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Видео:✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

📸 Видео

Площадь треугольника. Формула площади. Геометрия 8 класс.Скачать

Как найти площадь треугольникаСкачать

Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Как найти площадь треугольникаСкачать

КАК НАЙТИ ПЛОЩАДЬ ТРЕУГОЛЬНИКА НА ЕГЭ? #shorts #егэ #огэ #профильныйегэ #треугольник #площадьСкачать

Задача найти площади треугольников при пересечении медианСкачать

Площадь по теореме Герона #математика #площадь #треугольник #герона #егэ #огэ #найтиплощадь #теоремаСкачать

18 ЗАДАНИЕ ОГЭ НАЙТИ ПЛОЩАДЬ ТРЕУГОЛЬНИКАСкачать

Как найти площадь этого треугольника, не зная формулы?Скачать

Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать