Abcda1b1c1d1 прямоугольный параллелепипед какая из прямых параллельна плоскости a1ad

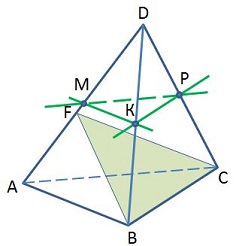
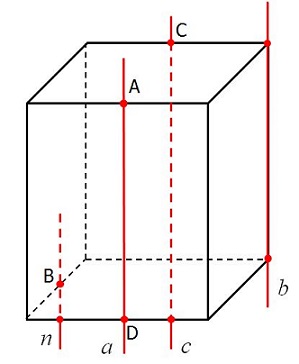
Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FАB.

Комментарий:
1) МК – средняя линия треугольника ADB, следовательно МК || АВ.
2) АВ лежит в плоскости FАB, следовательно по признаку параллельности прямой и плоскости МК || FАВ

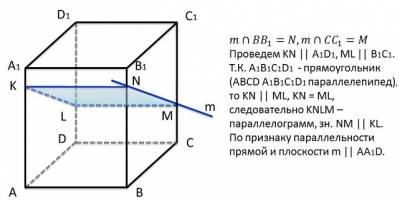
АВСDA ₁ B₁ C₁ D₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A₁ AD?

Комментарий:

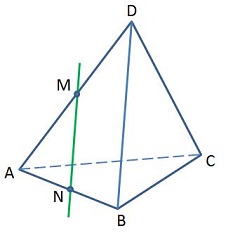
В тетраэдре DАВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN?

Комментарий:
MN – средняяя линия треугольника ADB, значит MN || DB. По признаку параллельности прямой и плоскости MN || DBC.

Выберите ВЕРНЫЕ высказывания:

1Параллельные прямые не имеют общих точек.2Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.3Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.4Существует параллелепипед, у которого все углы граней острые

Комментарий
«Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.»
Высказывание № 1 – верно. «не пересекаются», значит не имеют общих точек
Высказывание № 2 – неверно. не каждая прямая, лежащая в параллельной для данной прямой плоскости, так же будет лежать в одной плоскости с этой прямой.
Высказывание № 3 – верно. Линия пересечения плоскостей – это прямая, принадлежащая каждой из этих плоскостей, следовательно данная прямая параллельна данным плоскостям по признаку параллельности прямой и плоскости.
Высказывание № 4 – не верно. грани параллелепипеда – параллелограммы, противоположные стороны каждого из которых параллельны, следовательно углы при них и секущей (смежная сторона) в сумме равны 180 0
Если все углы граней будут острыми, то сумма одностосронних углов будет меньше 180 0 . Получили противоречие.

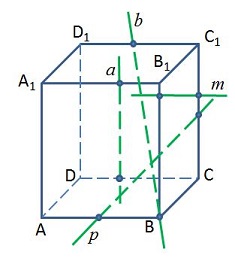
Точки А, В, С и D – середины ребер прямоугольного параллелепипеда. Назовите параллельные прямые.

1a || n2a || b3b || c4a || c

Комментарий
a || b, т.к. каждая из этих прямых параллельна одному и тому же ребру параллелепипеда – линии пересечения плоскостей, в которых лежат данные прямые.

Самостоятельная работа «Параллельность прямых и плоскостей»

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Точки М, Р, К – середины ребер DA , DB , DC тетраэдра DABC . Назовите прямую, параллельную плоскости FBC

1) МР 2) РК 3) МК 4) МК и РК

АВС DA ₁ B ₁ C ₁ D ₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A ₁ B ₁ C ₁ ?

В тетраэдре D АВС ВК = КС, DP = PC . Плоскости какой грани параллельна прямая РК?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Две прямые в пространстве называются параллельными, если они не пересекаются.

2) Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо так же ей параллельна, либо лежит в этой плоскости.

3) Существует такая прямая, которая лежит в плоскости и параллельна прямой, пересекающей данную плоскость.

4) Скрещивающиеся прямые не имеют общих точек.

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

6 6. Могут ли прямая и плоскость иметь одну общую точку?

7. Верно ли, что если прямая не имеет с плоскостью общих точек, то эта прямая параллельна плоскости?

8. Верно ли, что любые четыре точки не лежат в одной плоскости?

9. Верно ли, что две прямые a и b перпендикулярны друг другу, если a II c и b II c ?

10. Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей

11. Верно ли, что если две стороны треугольника параллельны плоскости α, то и третья сторона параллельна плоскости α?

12. Верно ли, что если прямая с пересекает прямую a и не пересекает прямую b , параллельную прямой a , то b и c – скрещивающиеся прямые?

13. Две стороны параллелограмма параллельны плоскости α. Параллельны ли плоскость α и плоскость параллелограмма

14. Могут ли быть равны два непараллельных отрезка, заключенные между параллельными плоскостями?

15. Могут ли пересекаться плоскости, параллельные одной и той же прямой?

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Точки М, Р, К – середины ребер DA , DB , DC тетраэдра DABC . Назовите прямую, параллельную плоскости F А B .

1) МР 2) РК 3) МК 4) МК и РК

АВС DA ₁ B ₁ C ₁ D ₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A ₁ AD ?

В тетраэдре D АВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN ?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Параллельные прямые не имеют общих точек.

2) Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.

3) Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.

4) Существует параллелепипед, у которого все углы граней острые.

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

6. Могут ли прямая и плоскость иметь множество общих точек?

7. Верно ли, что через две параллельные прямые всегда можно провести плоскость?

8. Верно ли, что любые четыре точки лежат в одной плоскости?

9. Верно ли, что если прямые не пересекаются, то они скрещиваются?

10. Верно ли, что плоскости α и β параллельны, если две пересекающиеся прямые m и n плоскости α параллельны плоскости β?

11. Может ли каждая из двух скрещивающихся прямых быть параллельна третьей прямой?

12. Верно ли, что если плоскость содержит данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой?

13. Верно ли, что если две прямые параллельны некоторой плоскости, то они параллельны друг другу?

14. Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?

15. Прямые a и c параллельны, а прямые b и a пересекаются. Могут ли прямые b и c быть параллельными?

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 964 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 340 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Морозова Юлия ВасильевнаНаписать 41428 05.11.2017

Номер материала: ДБ-828856

05.11.2017 348

05.11.2017 243

05.11.2017 482

05.11.2017 413

05.11.2017 279

05.11.2017 249

05.11.2017 315

05.11.2017 3285

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Прямоугольный параллелепипед. Что это такое?

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

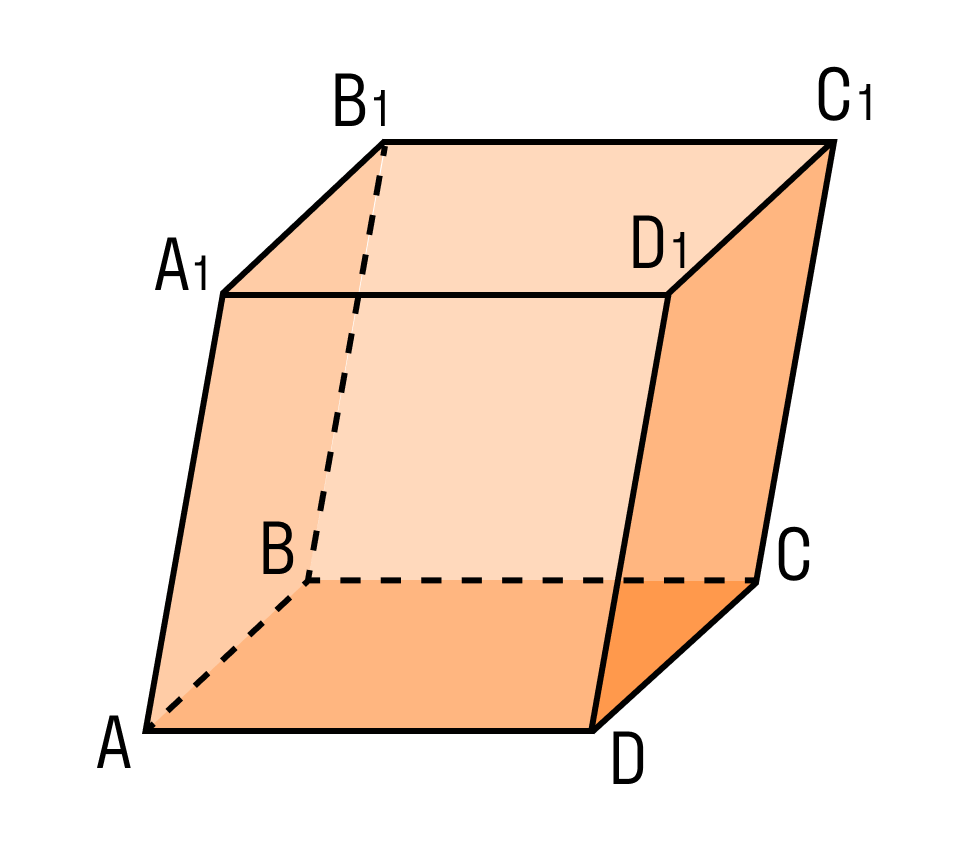
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

1. Противолежащие грани параллелепипеда равны и параллельны друг другу.
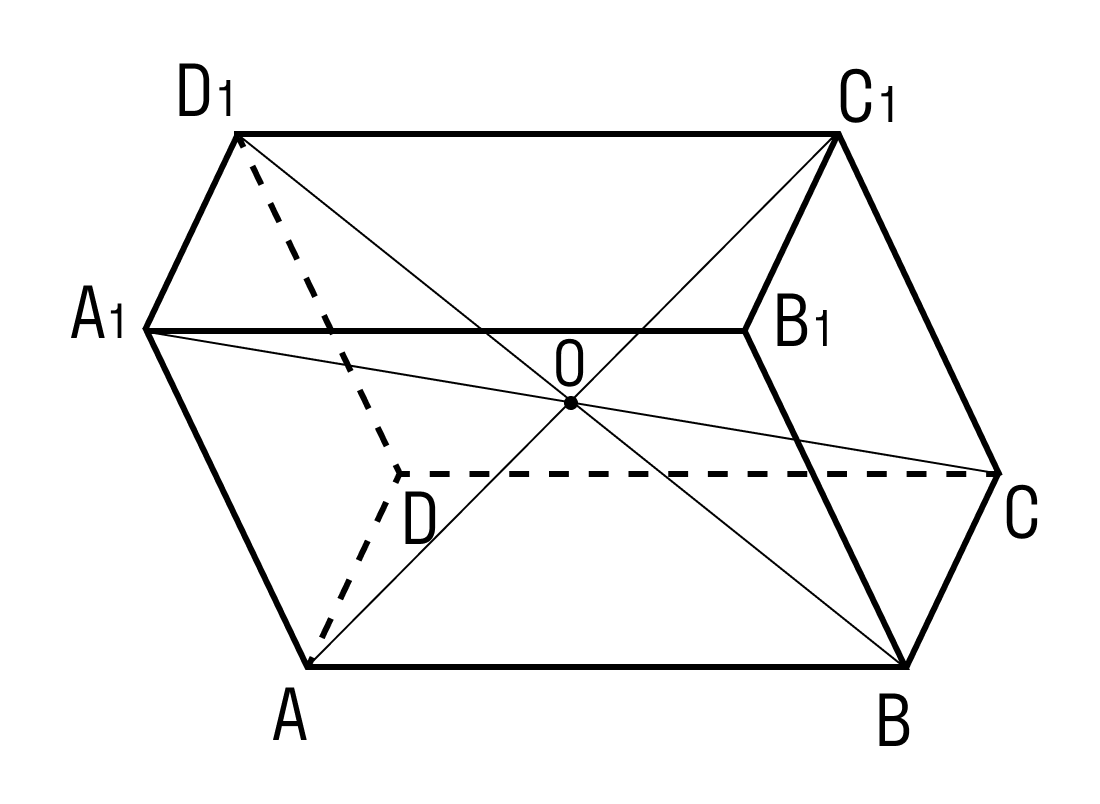
2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Параллелепипед симметричен относительно середины его диагонали.
4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
3. Высота прямого параллелепипеда равна длине бокового ребра.
4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

• Площадь боковой поверхности прямого параллелепипеда
  Sб = Ро*h
  Ро — периметр основания
  h — высота
• Площадь полной поверхности прямого параллелепипеда
  Sп = Sб+2Sо
  Sо — площадь основания
• Объем прямого параллелепипеда
  V = Sо*h

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

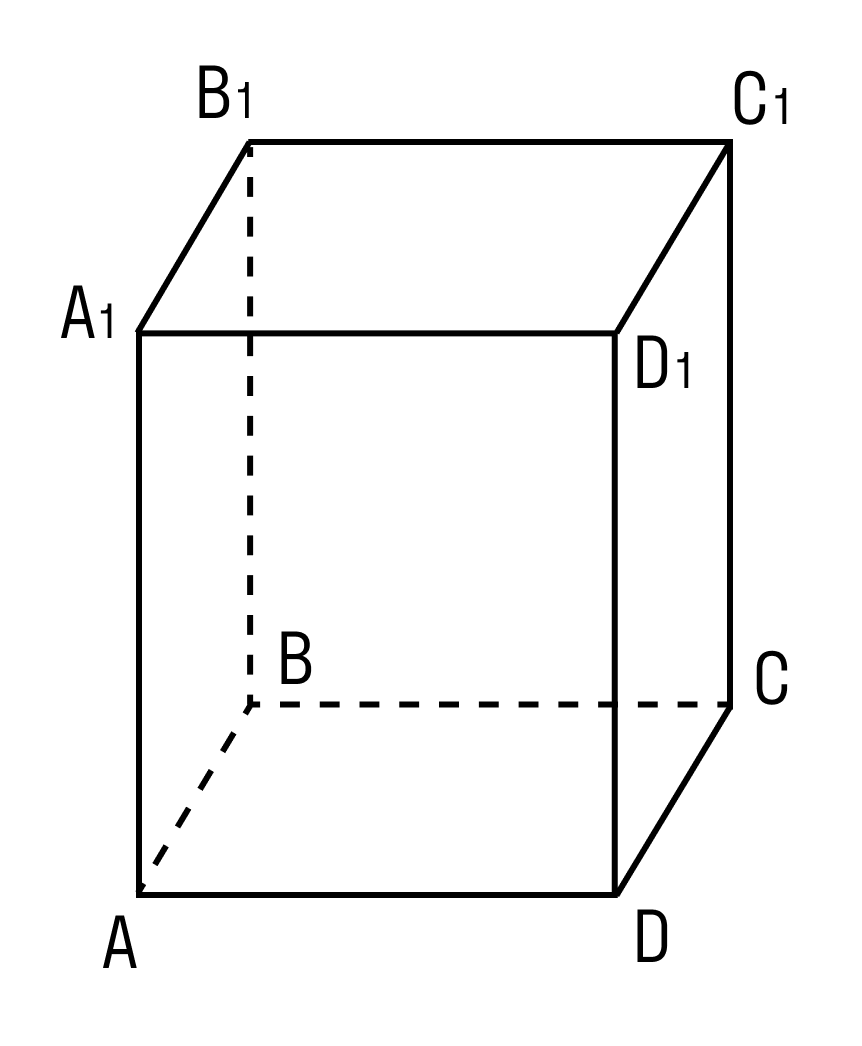
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
2. Противолежащие грани параллелепипеда попарно параллельны и равны.
3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
4. Диагонали прямоугольного параллелепипеда равны.
5. В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

• Объем прямоугольного параллелепипеда
  V = a · b · h
  a — длина, b — ширина, h — высота
• Площадь боковой поверхности
  Sбок = Pосн·c=2(a+b)·c
  Pосн — периметр основания, с — боковое ребро
• Площадь поверхности
  Sп.п = 2(ab+bc+ac)

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

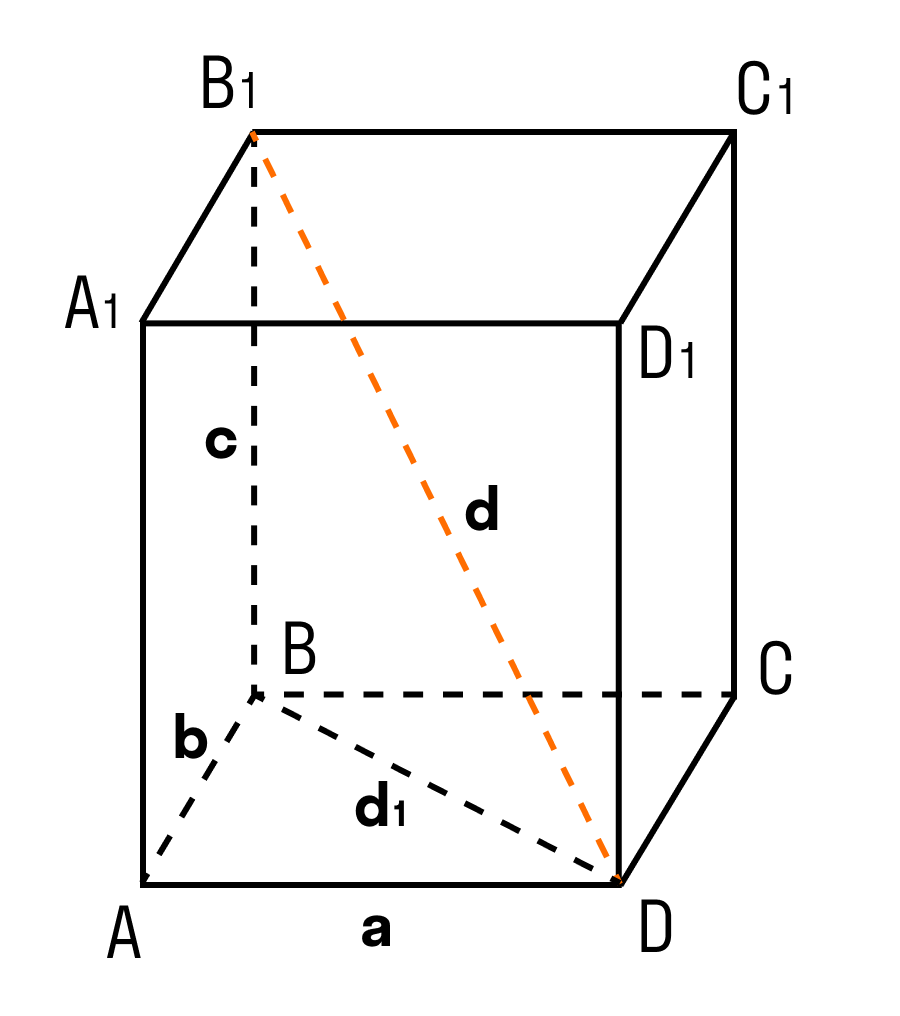
Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

1. В кубе 6 граней, каждая грань куба — квадрат.
2. Противолежащие грани параллельны друг другу.
3. Все углы куба, образованные двумя гранями, равны 90°.
4. У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
5. Диагонали куба равны.
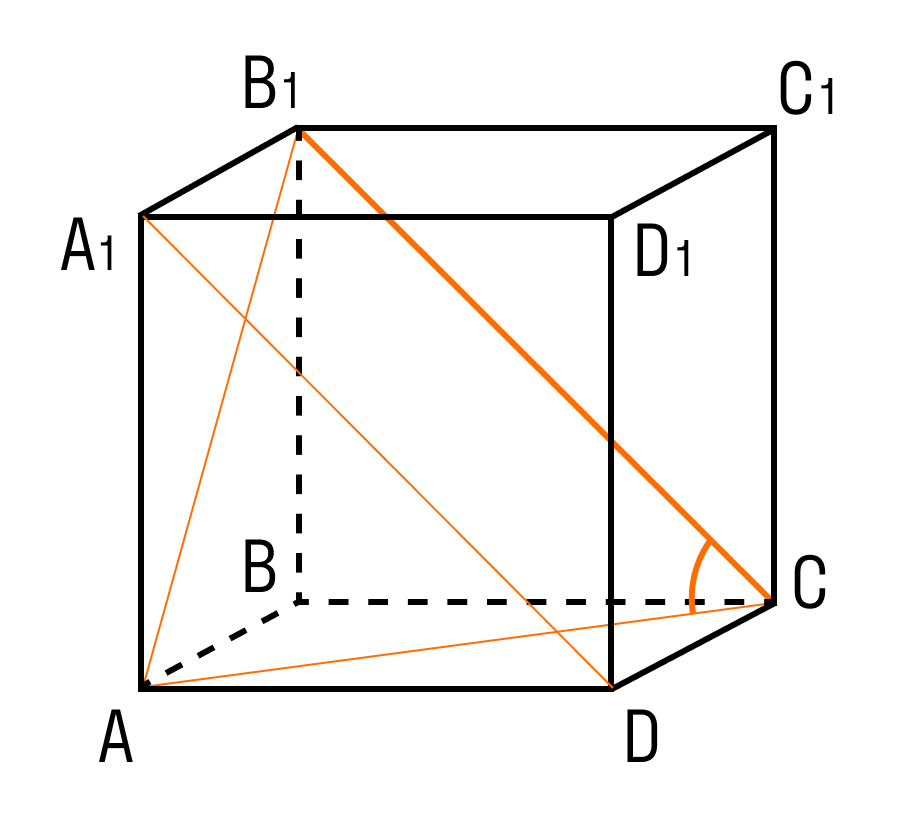
6. Диагональ куба в √3 раз больше его ребра.
7. Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

• Объем куба через длину ребра a
  V = a3
• Площадь поверхности куба
  S = 6a2
• Периметр куба
  P = 12a

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

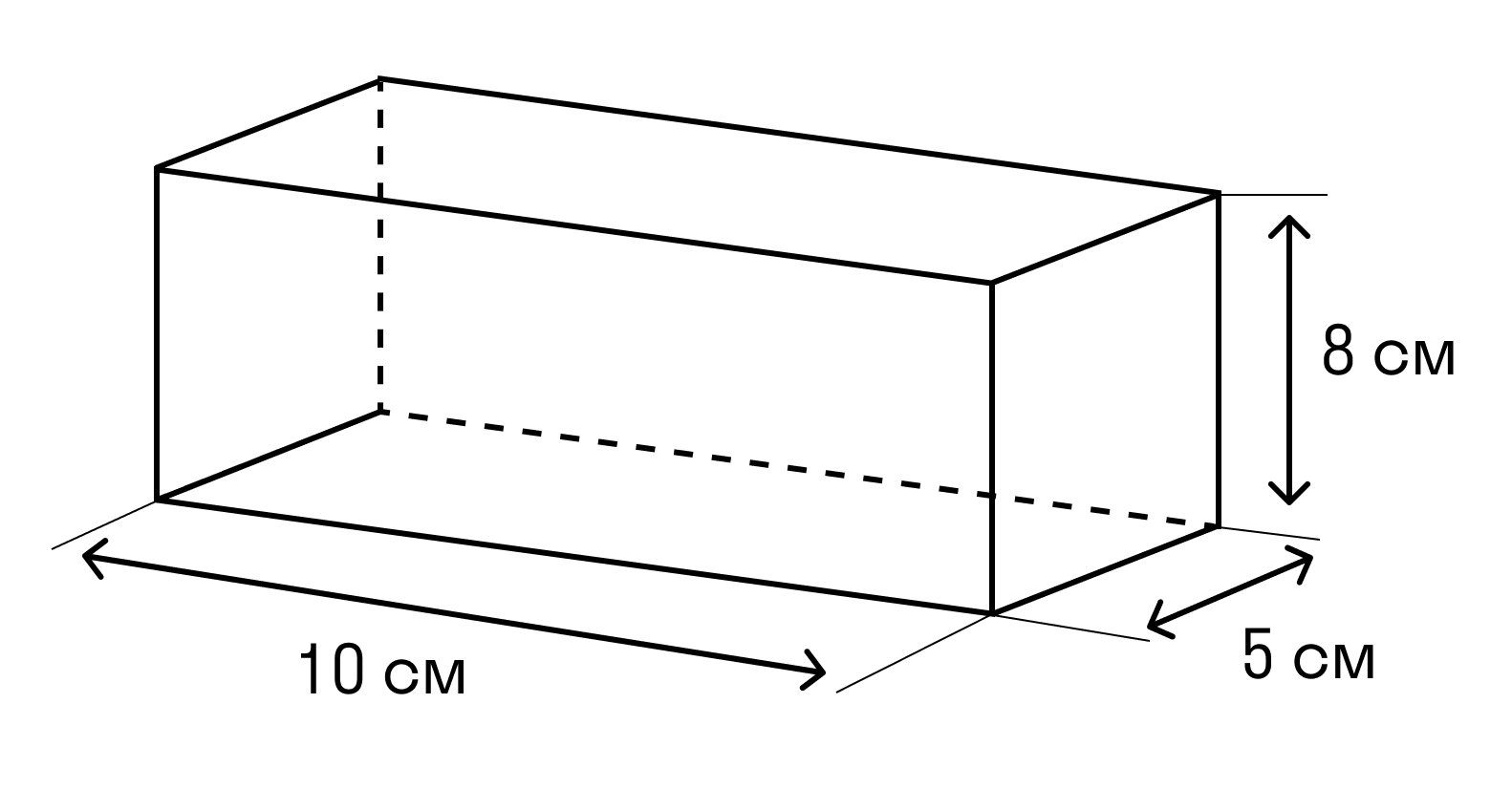
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

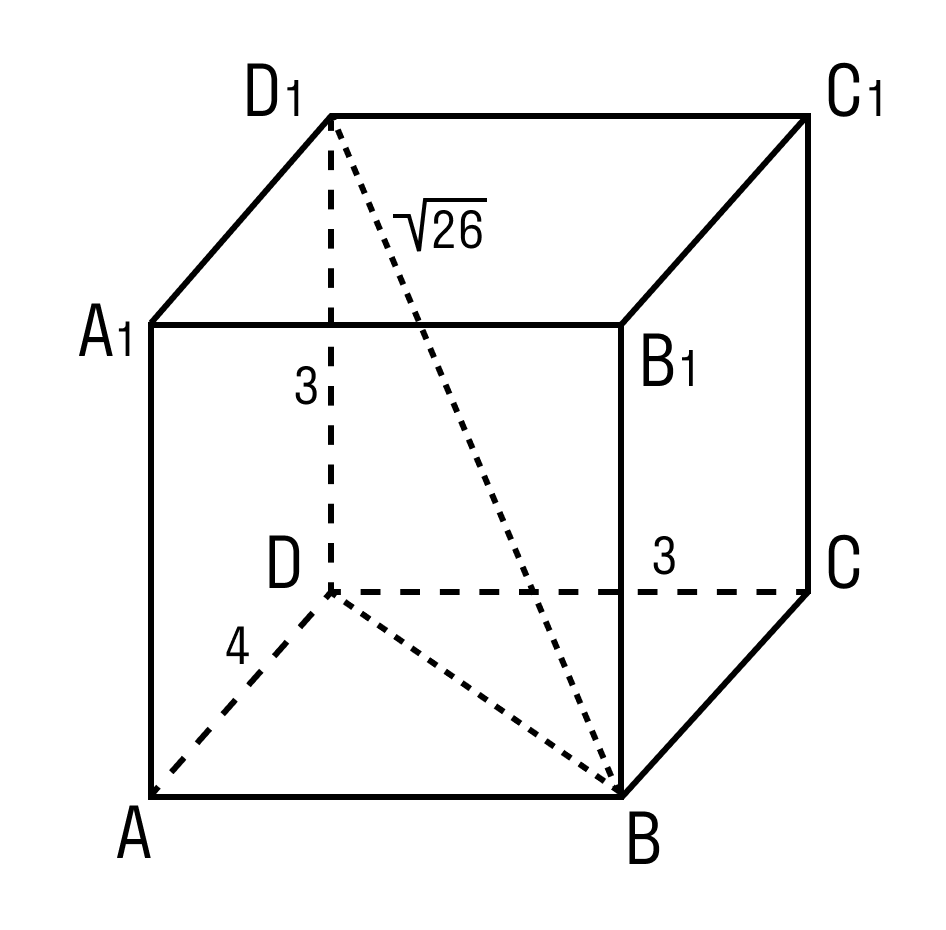
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁ 2 = DD₁ 2 + BD 2
BD 2 = BD₁ 2 – DD₁ 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 — AD 2 = (√17)2 — 4 2 = 1
A₁B₁ = AB = 1.

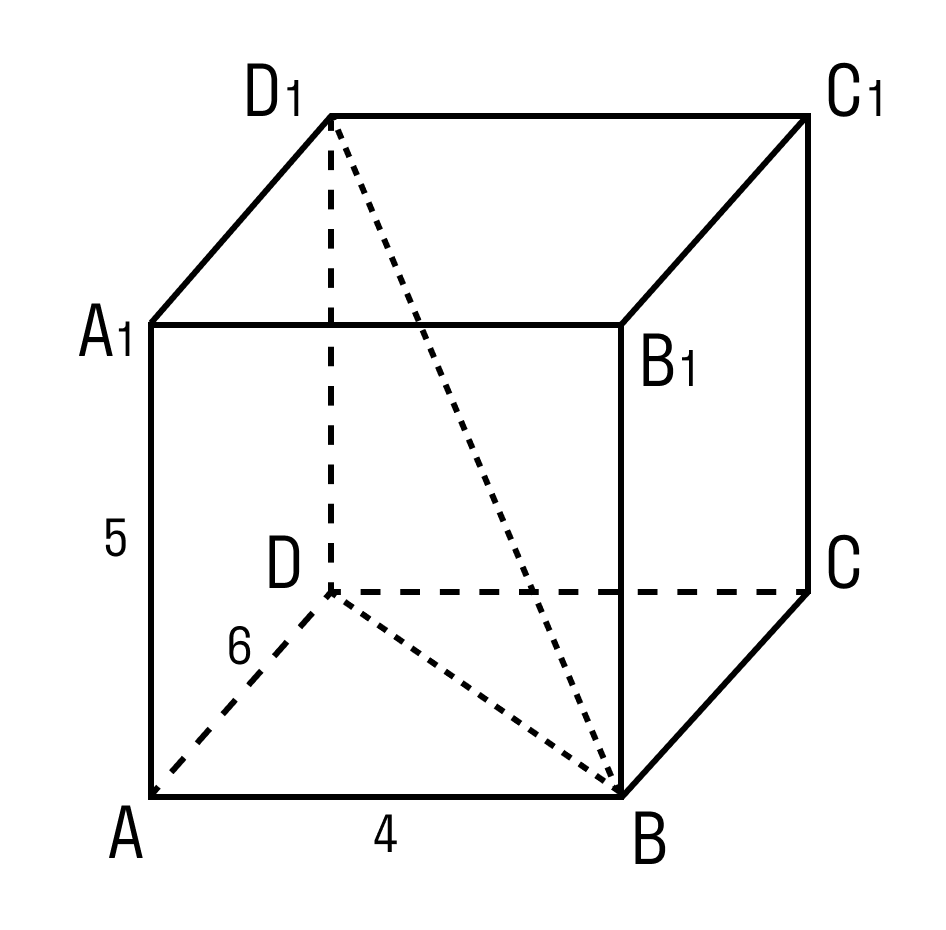
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77
BD₁ = √77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

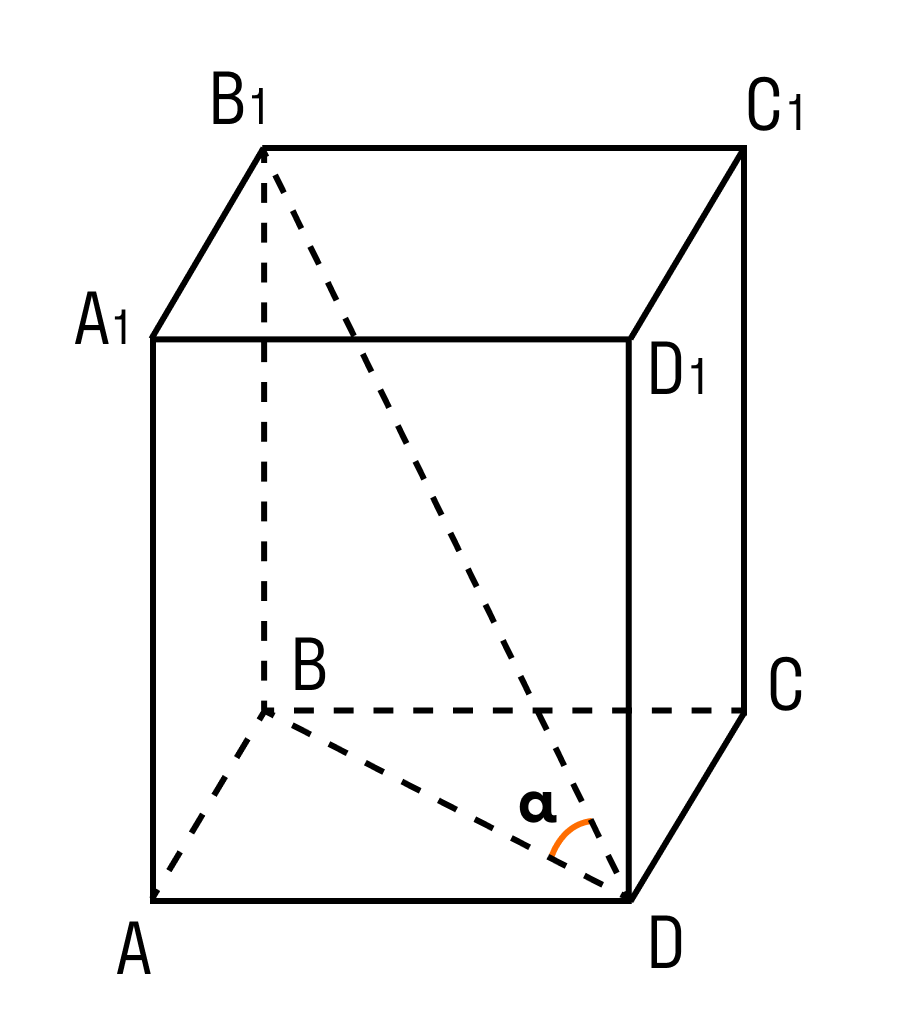
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

• прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
• параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
• основание прямоугольного параллелепипеда — прямоугольник;
• три измерения прямоугольного параллелепипеда: длина, ширина, высота;
• диагональ параллелепипеда равна сумме квадратов его измерений.

📺 Видео