Как построить призму в окружности (7 видео)

Комплексный чертеж призмы

Разделы: Технология

Цели и задачи уроки.

Закрепление навыков и умений по построению плоских и аксонометрических проекций 6-угольной призмы, построение сечения призмы и определение его натуральной величины, построение развертки.
Воспитание культуры труда, формирование познавательного интереса к предмету, инженерному делу.
Развитие пространственных представлений, пространственного мышления.

Оборудование:

модели геометрических тел,
шаблоны для построения 6-и угольника в изометрии,
развертка 6-и угольной призмы,
чертежные инструменты и принадлежности.

План занятия.

Повторение: положение прямых и плоскостей в пространстве, способы преобразования чертежа.
Новый материал.

2.1. Многогранники
2.2. Сечение многогранников

2.3. Построение 6-угольной призмы с сечением фронтально-проецирующей плоскостью.
2.4. Построение развертки усеченной призмы.

Ход занятия

1. Вопросы для повторения:

Какие бывают прямые и плоскости?

— Общего и частного положения.

Как располагаются в пространстве проецирующие прямые и проецирующие плоскости?

— Они перпендикулярны плоскостям проекций.

Назовите способы преобразования чертежа.

— Способ вращения, способ перемены плоскостей проекций.

Когда применяется способ перемены плоскостей проекций?

— Когда требуется определить натуральную величину наклонного сечения для построения развертки геометрического тела.

2. Записываем новую тему “Многогранники”.

Форма многих технических деталей представляет собой сочетание простых геометрических тел. Поэтому для выполнения чертежей изделий необходимо знать, как правильно изображаются различные геометрические тела. Рассмотрим построение на комплексном чертеже основных геометрических тел: призмы, пирамиды, цилиндра, конуса, сферы, тора.

Призма.

Призмой называется многогранник, у которого 2 грани (основания) — равные многоугольники с соответственно параллельными сторонами, а боковые грани – прямоугольники (у прямой призмы) или параллелограммы (у наклонной). Мы рассмотрим прямую призму. Элементы призмы: вершины, ребра (боковые и основания), грани (2 основания и боковые).

Рассмотрим 3 проекции 6-угольной призмы. На главном виде – это прямоугольники, боковые ребра – это горизонтально проецирующие прямые, 6-угольник на виде сверху представляет собой проекцию обоих оснований.

Сечение призмы выполнено фронтально-проецирующей плоскостью.

Сечение поверхности геометрических тел плоскостью называется плоская фигура, точки которой принадлежат и поверхности тела, и секущей плоскости. Сечение широко применяется в техническом черчении для выявления формы и внутреннего устройства предметов. В сечении многогранника плоскостью образуется многоугольник. Вершины многоугольника – это точки пересечения ребер многогранника с секущей плоскостью, стороны – это линии пересечения секущей плоскости с гранями многогранника.

Задача на построение комплексного чертежа усеченного многогранника состоит из решения следующих вопросов:

Построение проекций фигуры сечения.
Определение натуральной величины сечения.
Построение развертки отсеченной части.
Построение аксонометрического изображения отсеченной части.

Рассмотрим все поставленные задачи.

Задача 1. (см. Рис. 1).

Для построения трех проекций усеченной призмы выполняем следующие операции:

Строим 3 проекции правильной 6-угольной призмы, сторона основания а = 30, высота — произвольная.
Проводим фронтально-проецирующую секущую плоскость А-А.
На горизонтальной проекции плоскость сечения совпадает с проекцией основания ABCDEF, на профильной проекции сечение строится путем определения профильных проекций точек 1,2,3,4,5,6 и их последовательного соединения.

Задача 2. (см. Рис. 1).

Решение задачи 2 проводится с использованием чертежа, полученного при решении задачи 1. Для определения натуральной величины сечения используем метод вспомогательных секущих плоскостей. Для решения задачи выполняем следующие операции:

На произвольном расстоянии и параллельно секущей плоскости А-А проводим прямую. От фронтальных проекций точек 1, 2, 3, 4, 5, 6 проводим прямые, которые будут перпендикулярны плоскости сечения. Прямые проводим до пересечения с новой плоскостью проекций.
Новые проекции точек 1, 2, 3, 4, 5, 6 получаем перенося горизонтальные проекции данных точек в новую систему координат.
Полученный 6-и угольник в новой системе плоскостей проекций и будет являться натуральной величиной сечения 6-угольной призмы.

Задача 3. (см. Рис. 2).

Разверткой (выкройкой) поверхности тела называется плоская фигура, полученная путем совмещения всех точек данной поверхности с плоскостью без разрывов и складок.

Построение разверток выполняется обычно графическими приемами, с применением способов, предлагаемых начертательной геометрией. Построение развертки поверхности многогранника сводится к определению истинной величины каждой его грани по чертежу многогранника (см. Рис. 1). После этого грани многогранника стыкуются (соединяются) по ребрам и вершинам.

Для решения задачи 3 выполняем следующие операции:

Проводим горизонтальную прямую, на которой от произвольно выбранной точки А, откладываем отрезки AB, BC, CD, DE, EF, FA, равные длине стороны основания а = 30.

Из точек A, B, C, D, E, F, A восстанавливаем перпендикуляры и на них откладываем величины ребер усеченной призмы. Величины данных отрезков A1, B2, C3, D4, E5, F6, A1 берем с фронтальной проекции усеченной призмы. Полученные точки соединяем и получаем развертку боковой поверхности призмы.

К одному из отрезков основания, например к BC, пристраиваем 6-угольник ABCDEF.

К одному из звеньев ломаной, например, к отрезку 2-3, пристраиваем 6-угольник 123456 (сечение призмы), который переносим, используя метод засечек, с рисунка 1.

Рис 1

Рис 2

Задача 4. (см. рис. 3)

Строим усеченную 6-и угольную призму в изометрии. Сторона основания призмы, а = 30. Для выполнения задачи учащимся раздаются трафареты 6-и угольника в изометрии. Высоты A1, B2, C3, D4, E5, F6 – берем с фронтальной проекции усеченной призмы.

Содержание

Как научиться правильно изображать призму
Рисуем четырехгранную призму
Шестигранная призма
Зачем уметь строить эту геометрическую фигуру?
Линейно-конструктивный рисунок шестигранной призмы
Горизонтальный шестиугольник
Вертикальный шестиугольник
Вертикальный шестиугольник
📹 Видео

Видео:Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Как научиться правильно изображать призму

Главная страница » Основы Академического рисунка » Как построить призму. Правильное изображение фигуры на рисунке

Овладеть базовыми знаниями в области рисунка необходимо каждому начинающему художнику, независимо от выбранного стиля живописи. Обучение рисунку происходит поэтапно, и одной из важнейших тем является построение геометрических фигур. Сначала ученики осваивают плоские объекты, а потом переходят к объемным – в частности, призмам.

В зависимости от фигуры, лежащей в основании, призма бывает треугольной, четырехугольной, пятиугольной и так далее. Рассмотрим процесс рисования на примере четырехгранной и шестигранной призмы.

Видео:Построение пятиугольника циркулемСкачать

Рисуем четырехгранную призму

Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они – это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.

Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).

Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.

Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.

Видео:Как начертить ПРИЗМУ ПЯТИГРАННУЮ в изометрииСкачать

Шестигранная призма

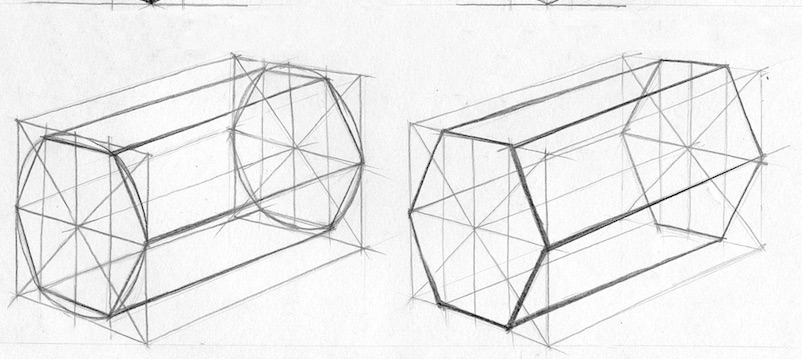
Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.

Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.

Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.

Видео:Как начертить УСЕЧЕННУЮ ПРИЗМУ В ОБЪЕМЕ и ее РАЗВЕРТКУСкачать

Зачем уметь строить эту геометрическую фигуру?

Научиться изображать геометрические тела, в том числе и призмы, необходимо всем будущим художникам.

С построения этих объектов начинается учебный процесс во всех заведениях. А уже после этого студенты постепенно переходят к изображению розеток, капителей, портрета и фигуры человека.

Если вы освоите этот объект, то в дальнейшем вам будет проще изображать различные предметы, строящиеся на его основе. В частности, у вас не возникнет трудностей с различными коробками и упаковками, бытовой техникой, зданиями и так далее.

Рисование геометрических тел также входит и в экзаменационную программу для поступления в художественный вуз. Однако с первого раза построить правильную фигуру с соблюдением пропорции и перспективы получается далеко не у каждого. Поэтому будет лучше, если в процессе подготовки к экзаменам вы потратите на изображение призмы достаточно времени, тогда на самом вступительном испытании будете чувствовать себя уверенно. С каждым разом изображение призмы будет даваться все легче.

В школе-студии К.Э. Арутюновой «Мастер рисунка» учат работать с геометрическими телами. К каждому ученику применяется индивидуальный подход с учетом его уровня и времени до сдачи вступительного экзамена. Преподаватель подробно разбирает со студентами все работы, обращает внимание на ошибки и помогает их исправить.

Готовитесь ли вы к поступлению в художественный вуз или просто хотите научиться для себя, без основ вам не обойтись. Независимо от того, в каком стиле вы собираетесь работать позднее, начать изучение все равно необходимо с базовых знаний. Запишитесь на занятия по телефону в Москве или через специальную форму на сайте.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Линейно-конструктивный рисунок шестигранной призмы

ЦЕЛЬ ЗАДАНИЯ. Научиться изображать шестигранную призму в различных положениях.

ПОСТАНОВКА ЗАДАНИЯ. Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести.

Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5— 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6— 1 и 4— 3 параллельны прямой 5— 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения.
Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.

Горизонтальный шестиугольник

Изобразите горизонтальный эллипс произвольного раскрытия, т.е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57).
Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5— 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5— 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5— 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).

Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.

Вертикальный шестиугольник

В таком шестиугольнике прямые, соединяющие точки 1 и 3, 6 и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5— 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и В, а на их пересечении с эллипсом найдите точки 7, 3, 6 и 4. Затем последовательно соедините точки 1— 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.

Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем
квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ постро
ения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5— 2 равен стороне квадрата, а по вертикали — меньше ее длины.

Вертикальный шестиугольник

Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5— 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68).
Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1/14 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).

Гэризонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).

Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.

Кроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.

Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему
на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78).

Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник
основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).