методическая разработка по геометрии по теме
Два варианта практической работы на построение вписанной и описанной окружностей треугольника. К сожалению, на просмотре в этом окне не высвечиваются готовые чертежи — просмотрите загруженные документы.
Дети с удовольствием «мучаются».
- Скачать:
- Предварительный просмотр:
- Решение задач. Окружность, описанная около треугольника 7 класс
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Геометрия в 9-м классе. Самостоятельные и практические работы
- Нахождение площади, периметра правильного многоугольника, его сторон и радиусов вписанной и описанной окружностей»
- Практическая работа на координатной плоскости по теме: «Движение»
- Самостоятельная работа по теме: «Правильные многоугольники».
- Практическая работа по теме: «Правильные многоугольники».
- 📽️ Видео
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| laboratornaya_rabota_po_geometrii_i.docx | 20.27 КБ |
| laboratornaya_rabota_po_geometriivar_ii.docx | 20.37 КБ |
Видео:Построить описанную окружность (Задача 1)Скачать

Предварительный просмотр:
[Введите текст][Введите текст]Вариант 1
Лабораторная работа по геометрии « ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ »
- Вписать окружности в треугольники:
Выводы: центр вписанной окружности треугольника лежит на ______________________________________________________________________________________________________________________________________________________________________________________________________________________________
- Описать окружности около треугольников:
Выводы: центр описанной окружности треугольника лежит на _______________________________________________________________________________________________________________Центр описанной окружности прямоугольного треугольника лежит _______________________________________________________________________________________________________________
Центр описанной окружности тупоугольного треугольника лежит _______________________________________________________________________________________________________________
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Решение задач. Окружность, описанная около треугольника 7 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Урок № 61 Тема: Решение задач Дата _______
научить применять полученные знания на практике, закрепить умения и навыки в процессе решения задач;
способствовать совершенствованию умения работы с чертежными инструментами, учебником;
формировать культуру решения задач, совершенствовать навыки общения.
Цель: создать условия для применения полученных знаний на практике, более глубокого усвоения знаний.
Оборудование, наглядные пособия: циркуль, линейка, доска, учебник, карточки с дидактическим материалом.
Тип урока: урок закрепления знаний, умений и навыков с элементами письменного контроля.
Методы: репродуктивные, практические
Проверка домашней работы
Актуализация учебного процесса (фронтальный опрос)
Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.
Теорема. Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.
Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон.
Теорема. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Практические задания (работа в группах).
С помощью шаблонов начертите окружность и «на глаз» постройте ее центр. Попробуйте пояснить методы нахождения места центра окружности (в случае, если центр не указан).
Начертите окружность с центром в точке О. На окружности отметьте три точки А, В, С. Проведите хорды АВ, ВС, СА. Как расположена окружность относительно Δ АВС?
Начертите окружность с центром в точке О. Проведите любые три прямые – касательные к окружности так, чтобы три касательные пересекались. Точки пересечения обозначьте буквами D,E,F. Как расположена окружность относительно Δ DEF?
Окружность, описанная около треугольника и вписанная в треугольник
Подведение итогов урока. Задание на дом
Глава III, § 1.2, 1.3, № (стр. 66-68) (А.Н. Шыныбеков Геометрия – 7)
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 988 человек из 78 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 310 человек из 68 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 673 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Построение равностронего треугольника.Скачать

Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 536 653 материала в базе
Материал подходит для УМК
«Геометрия», Погорелов А.В.
39. Окружность, описанная около треугольника
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 30.10.2018
- 1346
- 9
- 30.10.2018
- 939
- 27
- 29.10.2018
- 1545
- 33
- 29.10.2018
- 668
- 2
- 29.10.2018
- 1686
- 32
- 28.10.2018
- 270
- 0
- 28.10.2018
- 419
- 6
- 28.10.2018
- 693
- 2
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 30.10.2018 3688
- DOCX 204 кбайт
- 79 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Малюков Андрей Николаевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 7 месяцев
- Подписчики: 1
- Всего просмотров: 25342
- Всего материалов: 17
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Путин поручил обучать педагогов работе с девиантным поведением
Время чтения: 1 минута
В России планируют создадут сеть центров для подростков «группы риска»
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Минпросвещения определило порядок получения заключений на международные договоры
Время чтения: 1 минута
Новые курсы: школьные службы примирения, детская журналистика и другие
Время чтения: 15 минут
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия в 9-м классе. Самостоятельные и практические работы
Разделы: Математика
Нахождение площади, периметра правильного многоугольника, его сторон и радиусов вписанной и описанной окружностей»
Фамилия _______________________ класс_________
Заполните пустые клетки таблицы для правильного треугольника.
(a3 — сторона правильного треугольника, Р- периметр треугольника, S – площадь треугольника, R – радиус описанной окружности, r – радиус вписанной окружности)
Фамилия _______________________ класс_________
Заполните пустые клетки таблицы для правильного четырехугольника.
(a4 — сторона правильного четырехугольника, Р- периметр четырехугольника, S – площадь четырехугольника, R – радиус описанной окружности, r – радиус вписанной окружности)
Фамилия _______________________ класс_________
Заполните пустые клетки таблицы для правильного шестиугольника.
(a6 — сторона правильного шестиугольника, Р — периметр шестиугольника, S – площадь шестиугольника, R – радиус описанной окружности, r – радиус вписанной окружности)
Ответы:
Ответы:
Ответы:
Практическая работа на координатной плоскости по теме: «Движение»
Вариант №1
Даны точки в координатной плоскости: А(-1;2); В(4;0); С(-1;-2)
Все задания выполнить на разных координатных плоскостях.
1) Постройте ∆ А1В1С1 относительно начала координат и запишите координаты получившихся точек.
2) Постройте ∆ А22В2С2 относительно оси оу и запишите координаты получившихся точек.
3) Постройте ∆ А3В3С3 выполните поворот на 90° против часовой стрелки и запишите координаты получившихся точек.
4) Постройте ∆ А4В4С4 с помощью параллельного переноса на вектор СК, если К(3;-2) и запишите координаты получившихся точек.
Вариант №2
Даны точки в координатной плоскости: А(3;-2); В(-1;0); С(3;2)
Все задания выполнить на разных координатных плоскостях.
1) Постройте ∆ А1В1С1 относительно начала координат и запишите координаты получившихся точек.
2) Постройте ∆ А2В2С2 относительно оси оу и запишите координаты получившихся точек.
3) Постройте ∆ А3В3С3 выполните поворот на 90° против часовой стрелки и запишите координаты получившихся точек.
4) Постройте ∆ А4В4С4 с помощью параллельного переноса на вектор АК, если К(-1;-2) и запишите координаты получившихся точек.
Вариант № 3
Даны точки в координатной плоскости: А(3;-2); В(-1;0); С(3;2)
Все задания выполнить на разных координатных плоскостях.
1) Постройте ∆ А1В1С1 относительно точки Д(1;-1) и запишите координаты получившихся точек.
2) Постройте ∆ А2В2С2 относительно биссектрисы угла 1 и 3 координатной четверти, запишите координаты получившихся точек.
3)Постройте ∆ А3В3С3 выполните поворот на 90° по часовой стрелки и запишите координаты получившихся точек.
4) Постройте ∆ А4В4С4 с помощью параллельного переноса на вектор АК, если К(-1;-2) и запишите координаты получившихся точек.
Вариант №4
Даны точки в координатной плоскости: А(-1;2); В(4;0); С(-1;-2)
Все задания выполнить на разных координатных плоскостях.
1) Постройте ∆ А1В1С1 относительно точки Д(1;-1) и запишите координаты получившихся точек.
2) Постройте ∆ А2В2С2 относительно биссектрисы угла 1 и 3 координатной четверти, запишите координаты получившихся точек.
3)Постройте ∆ А3В3С3 выполните поворот на 90° по часовой стрелки и запишите координаты получившихся точек.
4) Постройте ∆ А4В4С4 с помощью параллельного переноса на вектор АК, если К(3;2) и запишите координаты получившихся точек.
Вариант №5
Даны точки в координатной плоскости: А(-2;-1); В(1;2); С( 2; 0); Д(0;-3)
Все задания выполнить на разных координатных плоскостях.
1) Постройте А1В1С1Д1 относительно начала координат и запишите координаты получившихся точек.
2) Постройте А2В2С2Д2 относительно осиox , запишите координаты получившихся точек.
3) Постройте А3В3С3Д3 выполните поворот на 45° по часовой стрелки и запишите координаты получившихся точек.
4) Постройте А4В4С4Д4 с помощью параллельного переноса на вектор ВК, если К(5;2) и запишите координаты получившихся точек.
Самостоятельная работа по теме: «Правильные многоугольники».
Вариант №1
- Какой многоугольник называется правильным? Приведите примеры.
- Найдите углы правильного десятиугольника.
- Найдите величину центрального угла правильного двенадцатиугольника.
Вариант №2
- Какой многоугольник называется правильным? Приведите примеры.
- Найдите углы правильного восьмиугольника.
- Сколько сторон имеет правильный многоугольник, если каждый вписанный угол равен 120°?
Вариант №3
- Какой многоугольник называется правильным? Приведите примеры.
- Найдите углы правильного десятиугольника.
- Найдите величину центрального угла правильного двенадцатиугольника.
Вариант №4
- Какой многоугольник называется правильным? Приведите примеры.
- Найдите углы правильного двенадцатиугольника.
- Сколько сторон имеет правильный многоугольник, если каждый вписанный угол равен 150°?
Вариант №5
- Какой многоугольник называется правильным? Приведите примеры.
- Найдите углы правильного десятиугольника.
- Найдите величину центрального угла правильного двенадцатиугольника.
Вариант №6
- Какой многоугольник называется правильным? Приведите примеры.
- Найдите углы правильного двенадцатиугольника.
- Сколько сторон имеет правильный многоугольник, если каждый вписанный угол равен 150°?
Практическая работа по теме: «Правильные многоугольники».
Вариант №1
- Начертите правильный треугольники постройте 2 окружности: а) вписанную в него, б) описанную около него.
- Докажите, что вершины правильного шестиугольника, взятые через одну, являются вершинами правильного треугольника.
- Сторона правильного восьмиугольника равна 8 см. Найдите большую диагональ.
- Назовите многоугольник, который получится, если последовательно соединить отрезками взятые через одну вершины правильного: шестиугольника, восьмиугольника (выполните построение).
Вариант №2
- Начертите правильный четырехугольник постройте 2 окружности: а) вписанную в него, б) описанную около него.
- Докажите, что вершины правильного восьмиугольника, взятые через одну, являются вершинами правильного четырехугольника.
- Сторона правильного шестиугольника равна 5см. Найдите большую диагональ.
- Назовите многоугольник, который получится, если последовательно отрезками соединить середины сторон правильного треугольника, шестиугольника (выполните построение).
Вариант №3
- Начертите правильный треугольники постройте 2 окружности: а) вписанную в него, б) описанную около него.
- Докажите, что вершины правильного шестиугольника, взятые через одну, являются вершинами правильного треугольника.
- Сторона правильного восьмиугольника равна 10 см. Найдите большую диагональ.
- Назовите многоугольник, который получится, если последовательно соединить отрезками взятые через одну вершины правильного: восьмиугольника, двенадцати угольника (выполните построение).
Вариант №4
- Начертите правильный четырехугольник постройте 2 окружности: а) вписанную в него, б) описанную около него.
- Докажите, что вершины правильного восьмиугольника, взятые через одну, являются вершинами правильного четырехугольника.
- Сторона правильного шестиугольника равна 7 см. Найдите большую диагональ.
- Назовите многоугольник, который получится, если последовательно отрезками соединить середины сторон правильного треугольника, четырехугольника (выполните построение).
Вариант №5
- Начертите правильный треугольники постройте 2 окружности: а) вписанную в него, б) описанную около него.
- Докажите, что вершины правильного шестиугольника, взятые через одну, являются вершинами правильного треугольника.
- Сторона правильного четырехугольника равна 8 см. Найдите большую диагональ.
- Назовите многоугольник, который получится, если последовательно соединить отрезками взятые через одну вершины правильного: шестиугольника, восьмиугольника, двенадцати угольника (выполните построение).
📽️ Видео
Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

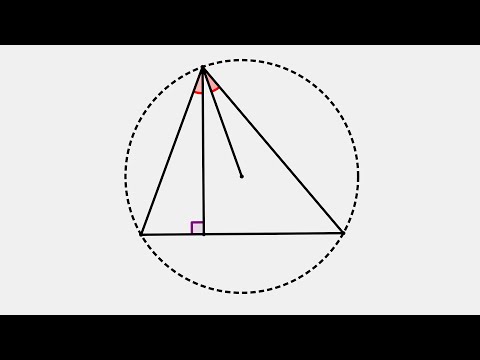
Изогонали угла. Радиус описанной окружности и высота, проведенные из одной вершины треугольника.Скачать
Задание 24 Площадь описанного треугольникаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Равносторонний треугольник. Описанная окружностьСкачать

№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Свойство окружности, описанной около равнобедренного треугольникаСкачать

Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Радиус описанной окружностиСкачать










