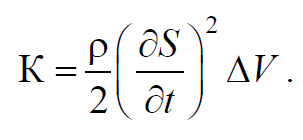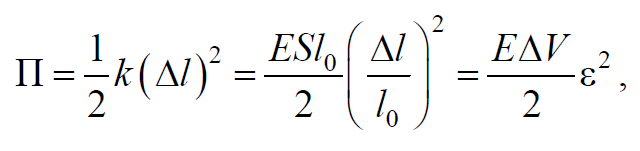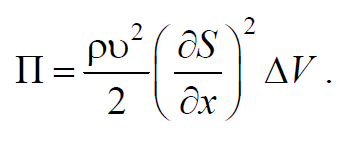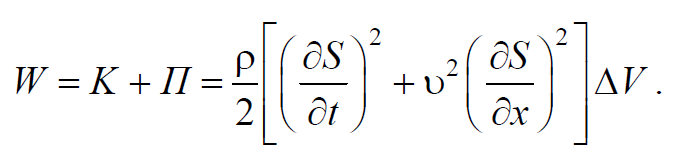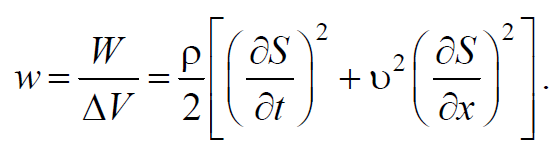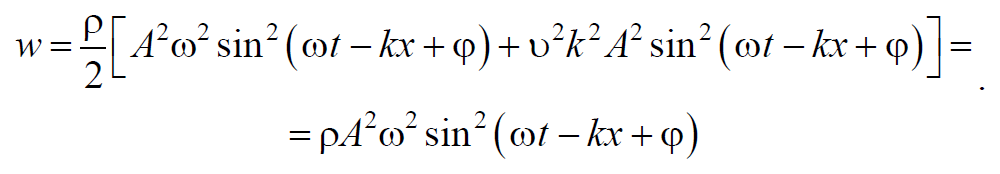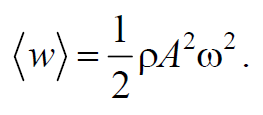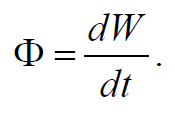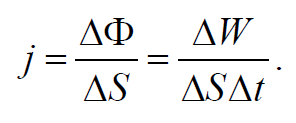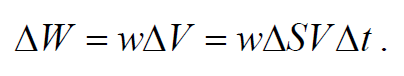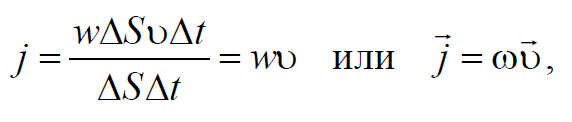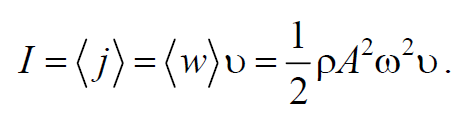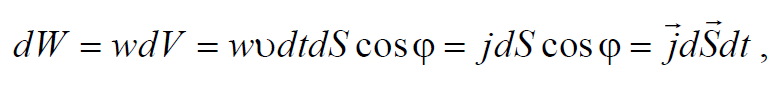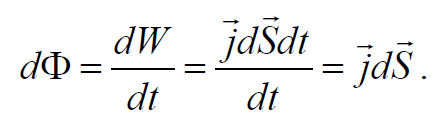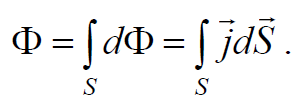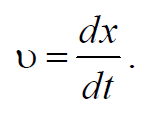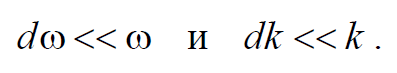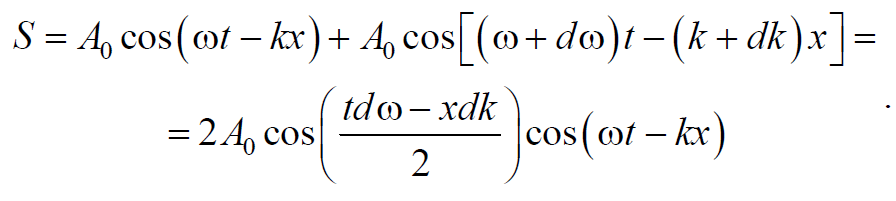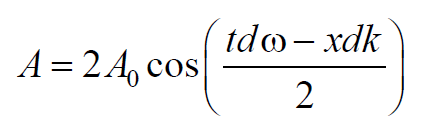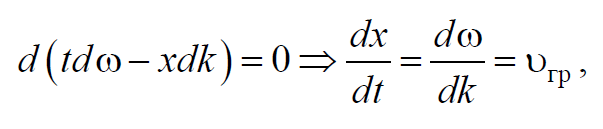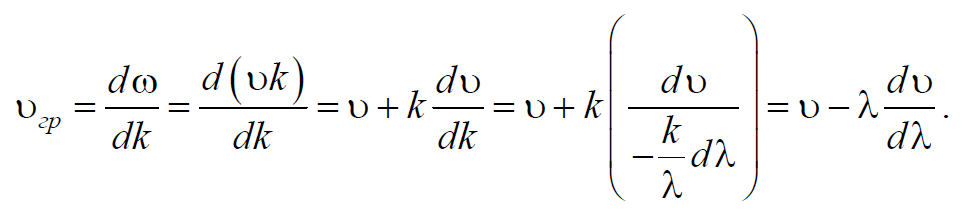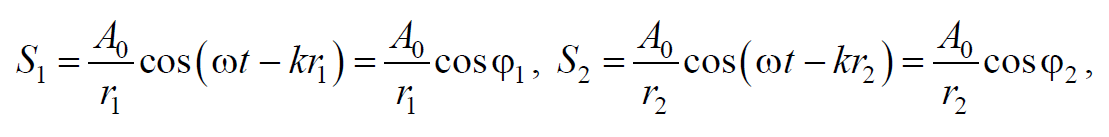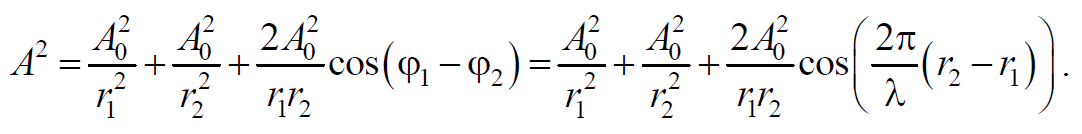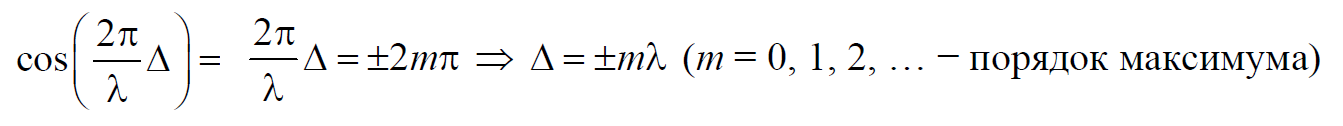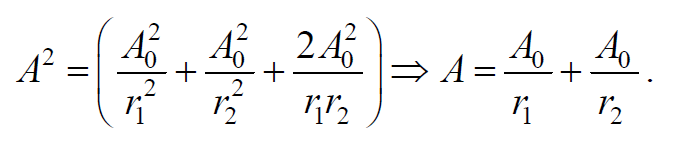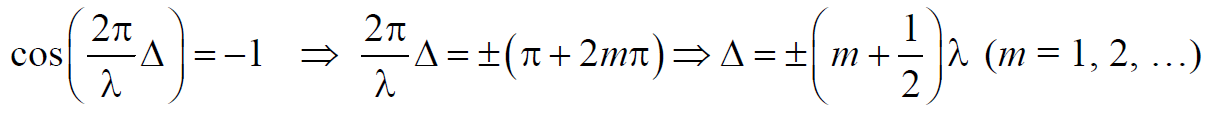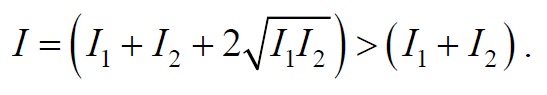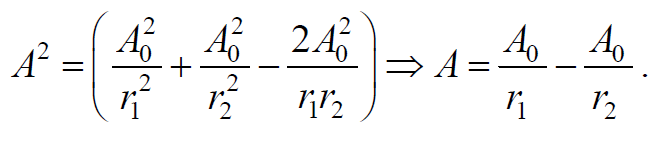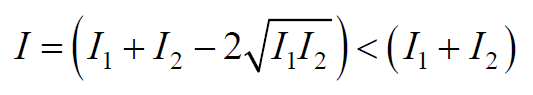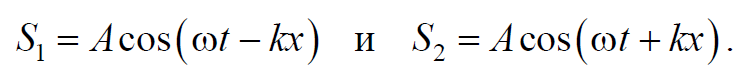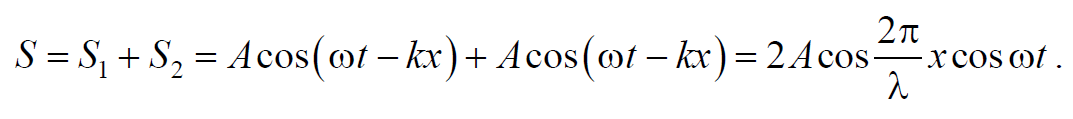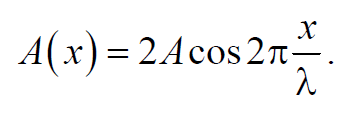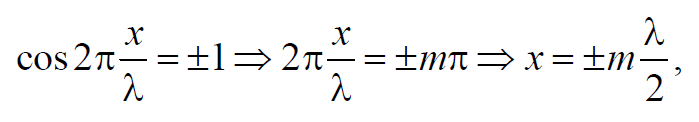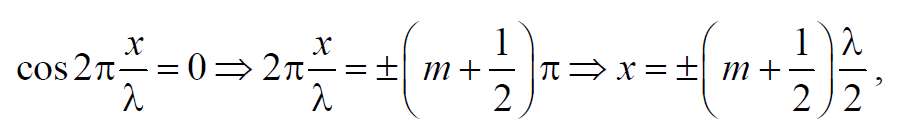Вектор плотности потока энергии волны поток энергии (3 видео)

Плотность потока энергии волны. Интенсивность волны

Распространение волн всегда связан с переносом энергии, который количественно характеризуется потоком энергии Ф, плотностью потока энергии J и интенсивностью волны I.

Рассмотрим волну, распространяющуюся вдоль оси о х со скоростью v (рис.210). Волна за время A t распространяется на расстояние, равное v • A t. Построим параллелепипед с основаниями A S, перпендикулярными оси ох, и длиной v — At.

Вся энергия волны, заключённая в параллелепипеде, за интервал времени A t пройдёт через правое основание A S. Обозначим энергию, переносимую волной сквозь площадку A S, через A W. Она равна произведению объёмной плотности полной энергии со _пол волны на объём параллелепипеда А V.,

Если объём V,, параллелепипеда мал, то объёмную плотность энергии со _пол волны можно считать одинаковой во всех точках рассматриваемого объёма.

Количество энергии, переносимое волной за единицу времени через поверхность AS, расположенную перпендикулярно направлению распространения волны, называется потоком Ф энергии волны

Поток энергии Ф в системе СИ измеряется в ваттах

(7 Вт =1 Л ж ). Поток энергии Ф волны может изменяться от одной

точки среды к другой. В этом случае используется векторная величина, называемая вектором плотности потока энергии J. Он был введён в 1874 г. профессором Московского университета Н. А. Умовым, поэтому назван вектором Умова.

Вектор Умова (вектор плотности потока энергии J) численно равен энергии, переносимой волной через единичную площадку, расположенную перпендикулярно направлению потока энергии в данной точке среды, за единицу времени

Запишем уравнение (20.56) в векторной форме

Вектор Умова, как и объёмная плотность полной энергии со ,_Ю1 волны, может иметь разные значения в разных точках пространства. В рассматриваемой точке среды вектор Умова изменяется со временем по такому же закону, как и объёмная плотность полной энергии со ,_Ю1 волны. Поэтому величина плотности потока энергии У через любую площадку (х = с о п s t), расположенную перпендикулярно направлению распространения волны, со временем периодически возрастает от нуля (У = 0) до максимального значения (У = У _тах).

В теории волн используется понятие среднего значения

плотности потока энергии за период времени Т (Т = xIL) в

где _пош) — среднее за период Т значение объёмной плотности

определённой точке пространства (х = с о п s t), которое назвали интенсивностью волны I

энергии волны в данной точке среды.

Подставим в (20.59) формулу (20.53)

Здесь учли, что среднее значение квадрата синуса за период Т равно 1.

Запишем формулу для интенсивности I волны, принимая во внимание выражение (20.60)

Отсюда следует, что интенсивность I волны прямо пропорциональна квадрату амплитуды А

Когда волна распространяется в трёхмерном пространстве, то поток энергии Ф через произвольную поверхность S определяется по формуле

где d S = п ? d S, п нормаль к поверхности S.

Плотность потока энергии J и интенсивность I в системе СИ

имеют размерность — ватт на квадратный метр | ^ т ].

Проведём две волновые поверхности в виде сфер, с радиусами г; и г₂. Считаем, что энергия волны не поглощается средой, тогда средние значения энергии, проходящей через волновые поверхности, равны

где S/, S₂ — площади сфер радиусами Г/ и г₂. Подставим в (20.62) интенсивности //, 1₂

сократив на р, у, со , получим

Итак интенсивность I сферической волны убывает по мере удаления от точечного источника по закону

где I 00), I (г) — интенсивность волны на расстояниях г = 1 м и произвольном расстоянии г от источника волны. Уравнение (20.65) следует из (20.63) и (20.64), записанных для двух расстояний г = 1 м и г > 1 м.

Зависимость амплитуды А и интенсивности I сферической волны от расстояния г от источника волны объясняются тем, что по мере удаления фронта волны от источника волн в колебательное движение за равные промежутки времени вовлекаются всё возрастающие объёмы среды.

Уравнение сферической волны записывается в виде

где г — расстояние от источника волн до рассматриваемой точки среды.

Интенсивность I и амплитуда А плоской волны, распространяющейся в среде, не поглощающей энергию волны, не изменяются при удалении от источника волн. Это связано с тем, что в колебательное движение за равные промежутки времени вовлекаются равные объёмы среды.

Интенсивность I плоской волны, распространяющейся в поглощающей среде вдоль положительного направления оси о х, изменяется, как и амплитуда волны по экспоненциальному закону

где I (0) — интенсивность волны в точке х = О, а — линейный коэффициент поглощения упругих волн.

Содержание

Энергия упругой волны. Поток и плотность потока энергии. Вектор Умова
Лекция №10. Механические волны
6.5. Волновой перенос энергии и его характеристики: поток, плотность потока, интенсивность
6.6. Фазовая и групповая скорости волн
6.7. Интерференция упругих волн
6.8. Стоячие волны
🔍 Видео

Видео:Средняя плотность потока энергии. вектор Пойнтинга.Скачать

Энергия упругой волны. Поток и плотность потока энергии. Вектор Умова

Упругая среда, в которой распространяются механические волны, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией.

Рассмотрим продольную плоскую волну (8.2), которая распространяется в единице объема среды массой, равной р, с колебательной скоростью и = d^/dt , где | — смещение частиц среды. Выделенный объем обладает кинетической энергией. Объемная плотность кинетической энергии среды выражается как

где dV_k — кинетическая энергия всех частиц в малом объеме dV среды, выбранном таким образом, что в его пределах скорость и всюду одинакова; р — плотность среды; и — скорость колебания частиц среды.

Можно доказать, что объемная плотность потенциальной энергии упругодеформированной среды

где dV_p — потенциальная энергия однородно деформированного малого участка среды объемом dV v — фазовая скорость волны в среде; с — относительная деформация среды.

Поскольку волна движется, то она осуществляет перенос механической энергии. Под объемной плотностью энергии упругих волн понимают объемную плотность механической энергии среды, обусловленную распространением этих волн:

Продифференцировав уравнение плоской волны (8.4) один раз по /, другой раз по х и определив таким образом и и с, с учетом того, что k 2 v 2 = о) 2 , получим плотность энергии, возникающей в упругой среде при распространении в ней плоской продольной волны:

Рис. 8.3. Через площадку среды dS за время dt волной переносится энергия dW

В физике используют понятие потока энергии. Если площадка среды имеет площадь dS, а ее нормаль п составляет с направлением распространения волны (осью X) угол а (рис. 8.3), то поток энергии d 2, с)).

Когда волна распространяется в трехмерном пространстве, тогда поток энергии через произвольную поверхность S выражается в виде интеграла:

Эффект Доплера для звуковых волн. При движении источника колебаний и приемника (устройства, которое воспринимает звуковые колебания среды) друг относительно друга происходит изменение частоты колебаний, воспринимаемой приемником. Это явление называется эффектом Доплера.

В акустике эффект Доплера проявляется как повышение тона звука при приближении источника звука к приемнику и понижение тона при удалении источника от приемника.

Пусть источник и приемник (наблюдатель) движутся вдоль соединяющей их прямой: и_и и v_u — соответственно скорости источника и приемника (положительны при сближении и отрицательны при удалении источника и приемника); v₀ — частота колебаний источника; и — скорость распространения звука в данной среде. Если направления у_и и v_u не совпадают с проходящей через источник и приемник прямой, то берут их проекцию на направление этой прямой.

В общем случае частота воспринимаемых приемником колебаний

Видео:Урок 374. Энергия, переносимая волной. Интенсивность сферической волныСкачать

Лекция №10. Механические волны

6.5. Волновой перенос энергии и его характеристики: поток, плотность потока, интенсивность

Пусть в некоторой среде распространяется в направлении оси 0х плоская продольная волна $$S=Acos(ωt-kx+φ)$$ . Выделим в среде элементарный объем ΔV , настолько малый, чтобы скорость движения и деформацию во всех точках этого объема можно было считать одинаковыми и равными. Выделенный объем обладает кинетической энергией $$K=mv^2$$ . Если масса $$m=ρΔV$$ , а $$v=$$ , то

Потенциальная энергия упругой деформации рассматриваемого объема

где $$k=$$ ; $$l_0$$ − первоначальная длина рассматриваемого объема; $$ε=$$ − относительная деформация объема; $$ΔV=$$ − первоначальный объем. Используя формулу (6.4.8) и, учитывая, что $$ε=$$ , получим

Тогда полная энергия упругой волны

Определим плотность энергии, разделив (6.5.4) на объем ΔV

Продифференцируем уравнение плоской продольной волны (6.2.8) по времени t и по координате х и подставим выражения в формулу (6.5.5) учтя, что $$k^2υ^2=ω^2$$

Среднее значение квадрата синуса равно 1/2. Соответственно среднее по времени значение плотности энергии в каждой точке среды равно

Таким образом, плотность энергии и среднее значение плотности энергии пропорциональны плотности среды ρ , квадрату частоты ω и квадрату амплитуды волны А .

Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Поток энергии Ф через данную поверхность равен энергии dW переносимой за время dt

Ф измеряется в ваттах.

Для характеристики распространения энергии в разных точках пространства вводится векторная величина, называема плотностью потока энергии. Плотность потока энергии численно равна потоку энергии через единичную площадку ΔS , помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

Если через площадку ΔS , перпендикулярную к направлению распространения волны, переносится энергия ΔW за время Δt , то плотность потока энергии равна

Рассмотрим объем цилиндра с основанием ΔS и высотой υΔt ( υ − фазовая скорость волны). В случае малого объема цилиндра, плотность энергии во всех точках цилиндра можно было считать одинаковой и поэтому энергию можно найти как произведение плотности энергии ω на объем ΔV=ΔSυΔt

Подставив выражение (6.5.10) в последнее выражение, получим

где j − вектор плотности потока энергии, называемый вектором Умова.

Интенсивность волны равна

Данное выражение справедливо для волны любого вида.

Определим поток энергии через поверхность S . Для этого разобьем поверхность на элементарные участки dS . За время dt через площадку dS пройдет энергия dW . Объем цилиндра, где вычисляется энергия, равен $$dV = υdtdScosϕ$$ . Тогда в этом объеме содержится энергия

где d S = n dS ; n − единичный вектор нормали к поверхности dS .

Поток энергии через элементарную поверхность dS

Поток энергии через поверхность S равен

6.6. Фазовая и групповая скорости волн

Скорость распространения волны есть скорость перемещения фазы и называется фазовой скоростью. Фазовая скорость равна

Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности, и к ним применим принцип суперпозиции волн: при распространении в линейной среде (т. е. среде снеизменяющимися свойствами) нескольких волн, каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.

Используя принципа суперпозиции, любая волна может быть представлена в виде волнового пакета. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства. Простейший волновой пакет двух распространяющихся вдоль положительного направления оси Х гармонических волн с одинаковыми амплитудами, близкими частотами и волновыми числами, причем

Эта волна отличается от гармонической тем, что ее амплитуда

медленно изменяющаяся функция координаты х и времени t .

За скорость распространения волнового пакета принимают скорость перемещения максимума амплитуды волны. При условии, что $$tdω-xdk=const$$ , получим

где υ_гр – групповая скорость. Рассмотрим связь между групповой и фазовой скоростями. Учитывая, что волновое число $$k=$$ и $$dk=-dλ=-dλ$$ , получим

В теории относительности доказывается, что групповая скорость υ_гр ≤ c , в то время как для фазовой скорости ограничений не существует.

6.7. Интерференция упругих волн

Для того чтобы рассмотреть интерференцию волн, введем понятие когерентности . Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связано с понятием когерентности. Волны называются когерентными , если разность их фаз остается постоянной во времени. При наложении в пространстве двух или нескольких когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн, и заключается в том, что колебания в одних точках усиливают, а в других ослабляют друг друга.

Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками $$S_1$$ и $$S_2$$ , колеблющимися с одинаковыми амплитудой, частотой, нулевой начальной фазой и постоянной разностью фаз. Запишем уравнения колебаний:

где $$r_1$$ и $$r_2$$ − расстояния от источников волн до рассматриваемой точки.

Амплитуда результирующей волны равна (сложение одинаково направленных колебаний)

Так как разность начальных фаз $$(ϕ_1-ϕ_2)=(r_2-r_1)=Δ=const$$ , то результат наложения двух волн в различных точках зависит от величины $$Δ=r_2-r_1$$ , называемой разностью хода волн.

В точках, где выполняется условие

Так как квадрат амплитуды колебаний пропорционален интенсивности волны, то получаем

То есть наблюдается усиление интенсивности (увеличение амплитуду) результирующей волны или интерференционный максимум.

2) В точках, где выполняется условие

То есть наблюдается ослабление интенсивности (уменьшение амплитуды) результирующей волны или интерференционный минимум.

Таким образом, в результате наложения двух когерентных волн в среде возникают колебания, амплитуда которых различна в разных точках среды, при этом в каждой точке среды получается или максимум амплитуды, или минимум амплитуды, или ее промежуточное значение − в зависимости от значения разности расстояний точки до когерентных источников. Интерференция света приводит к перераспределению энергии волны между соседними областями, хотя в среднем для больших областей энергия остается неизменной.

6.8. Стоячие волны

Рассмотрим интерференцию стоячих волн. Стоячие волны − это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Запишем уравнение двух плоских волн, распространяющихся вдоль оси Х в противоположных направлениях

Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны

Из данного уравнения видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда зависит от координаты х