На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
- Площадь круга
- 2 Пи р квадрат это формула
- Содержание
- История [ править | править код ]
- Использование многоугольников [ править | править код ]
- Доказательство Архимеда [ править | править код ]
- Не больше [ править | править код ]
- Не меньше [ править | править код ]
- Доказательство перегруппировкой [ править | править код ]
- Интегрирование [ править | править код ]
- Быстрая аппроксимация [ править | править код ]
- Метод удвоения Архимеда [ править | править код ]
- Улучшение Снелла-Гюйгенса [ править | править код ]
- Развитие формулы удваивания Архимеда [ править | править код ]
- Аппроксимация случайными бросаниями [ править | править код ]
- Конечная перегруппировка [ править | править код ]
- Обобщения [ править | править код ]
- 📹 Видео
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Площадь круга
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
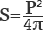
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Определение: Круг- это часть плоскости , ограниченная окружностью, круг является выпуклой фигурой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Видео:Площадь круга. Математика 6 класс.Скачать

2 Пи р квадрат это формула
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
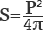
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Определение: Круг- это часть плоскости , ограниченная окружностью, круг является выпуклой фигурой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Перевод радиан в градусы.
Ad = Ar * 180 / пи
Где Ad — угол в градусах, Ar — угол в радианах.
Перевод градусов в радианы.
Ar = Ad * пи / 180
Где Ad — угол в градусах, Ar — угол в радианах.
Длина окружности.
L = 2 * пи * R
Где L — длина окружности, R — радиус окружности.
Длина дуги окружности.
L = A * R
Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах
Для окружности A = 2*пи (360 градусов), получим L = 2*пи*R.
Площадь треугольника.
S = (p * (p-a) * (p-b) * (p-c) ) 1/2
Где S — площадь треугольника, a, b, c — длины сторон,
p=(a+b+c)/2 — полупериметр.
Площадь круга.
S = пи * R 2
Где S — площадь круга, R — радиус круга.
Площадь сектора.
S = Ld * R/2 = (A * R 2 )/2
Где S — площадь сектора, R — радиус круга, Ld — длина дуги.
Площадь поверхности шара.
S = 4 * пи * R 2
Где S — площадь поверхности шара, R — радиус шара.
Площадь боковой поверхности цилиндра.
S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь полной поверхности цилиндра.
S = 2 * пи * R * H + 2 * пи * R 2
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Площадь боковой поверхности конуса.
S = пи * R * L
Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
Площадь полной поверхности конуса.
S = пи * R * L + пи * R 2
Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.
Объем шара.
V = 4 / 3 * пи * R 3
Где V — объем шара, R — радиус шара.
Объем цилиндра.
V = пи * R 2 * H
Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.
Объем конуса.
V = пи * R * L = пи * R * H/cos (A/2) = пи * R * R/sin (A/2)
Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.
Площадь круга с радиусом r равна πr 2 . Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1 ⁄2 × 2πr × r).
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Содержание
Видео:Лучший способ найти площадь кругаСкачать

История [ править | править код ]
Современные математики могут получить площадь круга с помощью методов интегрирования или вещественного анализа. Однако площадь круга изучалась ещё в Древней Греции. Евдокс Книдский в пятом столетии до нашей эры обнаружил, что площади кругов пропорциональны квадратам их радиусов. [1] Великий математик Архимед использовал методы евклидовой геометрии, чтобы показать, что площадь внутри окружности равна площади прямоугольного треугольника, основание которого имеет длину окружности, а высота равна радиусу окружности, в своей книге Измерение круга [en] . Длина окружности равна 2 π r, а площадь треугольника равна половине основания на высоту, что даёт π r 2 . До Архимеда Гиппократ Хиосский первый показал, что площадь круга пропорциональна квадрату его диаметра в его попытках квадрирования гиппократовых луночек [2] Однако он не установил константу пропорциональности.
Видео:Длина окружности и площадь кругаСкачать

Использование многоугольников [ править | править код ]
Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус. [3]
Видео:Почему площадь круга равна pi•R²Скачать

Доказательство Архимеда [ править | править код ]
Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.
Не больше [ править | править код ]
Предположим, что площадь круга C больше площади треугольника T = 1 ⁄2cr. Пусть E означает превышение площади. Впишем [en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G4 больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G8. Продолжаем деление, пока общий зазор Gn не станет меньше E. Теперь площадь вписанного многоугольника Pn = C − Gn должна быть больше площади треугольника.
G_ P_ &=C-G_ &>C-EP_ &>Tend>>»> E = C − T > G n P n = C − G n > C − E P n > T E&=C-T&>G_ P_ &=C-G_ &>C-EP_ &>Tend>> 
Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1 ⁄2nhs. Но h 1 ⁄2cr, получили противоречие.
Не меньше [ править | править код ]
Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G4 больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника Pn должна быть меньше T.
G_ P_ &=C+G_ & D = T − C > G n P n = C + G n C + D P n T =T-C&>G_ P_ &=C+G_ & 
Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.
Таким образом, площадь круга в точности равна площади треугольника.
Видео:Длина окружности. Площадь круга, 6 классСкачать

Доказательство перегруппировкой [ править | править код ]
Следуя Сато Мошуну [4] и Леонардо да Винчи [5] , мы можем использовать вписанные правильные многоугольники другим способом. Положим, мы вписали шестиугольник. Разрежем шестиугольник на шесть треугольников, делая сечения через центр. Два противоположных треугольника содержат общие диаметры. Сдвинем теперь треугольники, чтобы радиальные стороны стали смежными. Теперь пара треугольников образует параллелограмм, в котором стороны шестиугольника образуют две противоположные стороны длиной s. Две радиальные стороны становятся боковыми сторонами, а высота параллелограмма равна h (как в доказательстве Архимеда). Фактически, мы можем собрать все треугольники в один большой параллелограмм, располагая в ряд полученные параллелограммы (из двух треугольников). То же самое будет верно, если мы будем увеличивать число сторон. Для многоугольника с 2n сторонами параллелограмм будет иметь основание ns и высоту h. С ростом числа сторон длина основания параллелограмма увеличивается, стремясь к половине окружности, а высота стремится к радиусу. В пределе параллелограмм становится прямоугольником с шириной π r и высотой r.
| многоугольник | параллелограмм | |||||||
|---|---|---|---|---|---|---|---|---|
| n | сторона | основание | высота | площадь | ||||
| 4 | 1,4142136 | 2,8284271 | 0,7071068 | 2,0000000 | ||||
| 6 | 1,0000000 | 3,0000000 | 0,8660254 | 2,5980762 | ||||
| 8 | 0,7653669 | 3,0614675 | 0,9238795 | 2,8284271 | ||||
| 10 | 0,6180340 | 3,0901699 | 0,9510565 | 2,9389263 | ||||
| 12 | 0,5176381 | 3,1058285 | 0,9659258 | 3,0000000 | ||||
| 14 | 0,4450419 | 3,1152931 | 0,9749279 | 3,0371862 | ||||
| 16 | 0,3901806 | 3,1214452 | 0,9807853 | 3,0614675 | ||||
| 96 | 0,0654382 | 3,1410320 | 0,9994646 | 3,1393502 | ||||
| ∞ | 1/∞ | π | 1 | π | ||||
Видео:ПЛОЩАДЬ КРУГА. ЛАЙФХАК #math #логика #загадка #математика #геометрияСкачать

Интегрирование [ править | править код ]
Используя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице. Площадь бесконечно тонкого «слоя» радиуса t будет равна 2 π t dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.
A r e a ( r ) = ∫ 0 r 2 π t d t = [ ( 2 π ) t 2 2 ] t = 0 r = π r 2 . =int _ ^ 2pi t,dt&=left[(2pi ) > >
ight]_ ^ &=pi r^ .end
Можно разбивать круг не на кольца, а на треугольники с бесконечно малым основанием. Площадь каждого такого треугольника равна 1/2 * r * dt. Суммируя (интегрируя) все площади этих треугольников, получим формулу круга:
A r e a ( r ) = ∫ 0 2 π r 1 2 r d t = [ 1 2 r t ] t = 0 2 π r = π r 2 . =int _ ^ >r,dt&=left[ >rt
ight]_ ^ &=pi r^ .end
Видео:ЕГЭ Динамика вращения 5 модельных задачСкачать

Быстрая аппроксимация [ править | править код ]
Вычисления, проведённые Архимедом, были трудоёмкими и он остановился на многоугольнике с 96 сторонами. Более быстрый метод использует идеи Снелла (1621), позднее развитые Гюйгенсом (1654) [6] .
Метод удвоения Архимеда [ править | править код ]
Если задан круг, пусть un будет периметром вписанного правильного n-угольника, а Un — периметром описанного правильного n-угольника. Тогда un и Un являются нижней и верхней границей длины окружности, которые становятся точнее с ростом n, а их среднее значение (un + Un)/2 становится особенно хорошей аппроксимацией длины окружности. Чтобы вычислить un и Un для больших n, Архимед вывел следующие формулы:
u 2 n = U 2 n u n = u_ >>> 

Начав с шестиугольника, Архимед удваивал n четыре раза, дойдя до 96-угольника, который дал ему хорошую аппроксимацию длины окружности круга.
В современных обозначениях можно воспроизвести эти вычисления (и пойти дальше). Для единичной окружности вписанный шестиугольник имеет периметр u6 = 6, а описанный шестиугольник имеет периметр U6 = 4√3. Удваиваем семь раз, получаем
| k | n | un | Un | (un + Un)/4 |
|---|---|---|---|---|
| 6 | 6,0000000 | 6,9282032 | 3,2320508 | |
| 1 | 12 | 6,2116571 | 6,4307806 | 3,1606094 |
| 2 | 24 | 6,2652572 | 6,3193199 | 3,1461443 |
| 3 | 48 | 6,2787004 | 6,2921724 | 3,1427182 |
| 4 | 96 | 6,2820639 | 6,2854292 | 3,1418733 |
| 5 | 192 | 6,2829049 | 6,2837461 | 3,1416628 |
| 6 | 384 | 6,2831152 | 6,2833255 | 3,1416102 |
| 7 | 768 | 6,2831678 | 6,2832204 | 3,1415970 |
(здесь (un + Un)/2 аппроксимирует длину единичной окружности, которая равна 2 π , так что (un + Un)/4 аппроксимирует π )
Последняя строка таблицы содержит 355 ⁄113 — лучшее рациональное приближение, то есть не существует приближения лучшего этого со знаменателем до 113.
Число 355 ⁄113 является прекрасным приближением для π , нет рационального числа более близкого к π со знаменателем до 16604. [7]
Улучшение Снелла-Гюйгенса [ править | править код ]
Снелл предложил (а Гюйгенс доказал) более тесные границы, чем у Архимеда:
n 3 sin π n 2 + cos π n π n [ 2 sin π 3 n + tan π 3 n ] . >> >>>
Для n = 48 формула даёт приближение лучше (около 3,14159292), чем метод Архимеда для n = 768.
Развитие формулы удваивания Архимеда [ править | править код ]
Пусть одна сторона вписанного правильного n-угольника имеет длину sn и пусть точки A и B — её концы. Пусть A′ — противоположная A точка на окружности, так что A′A является диаметром, а A′AB является вписанным треугольником, опирающимся на этот диаметр. По теореме Фалеса этот треугольник является прямоугольным (угол B прямой). Пусть длина A′B равна cn и эту длину будем называть дополнением sn. Тогда cn 2 +sn 2 = (2r) 2 . Пусть точка C делит дугу AB пополам, и пусть C′ является противоположной C точкой окружности. Тогда длина CA равна s2n, длина C′A равна c2n, а C′CA снова является прямоугольным треугольником, опирающимся на диаметр C′C. Поскольку C делит дугу AB пополам, диаметр C′C перпендикулярен хорде AB, которую он пересекает, скажем, в точке P. Треугольник C′AP тогда прямоуголен и подобен C′CA, поскольку у них общий угол C′. Получаем, что все три соответствующие стороны находятся в одной и той же пропорции. В частности, мы имеем C′A : C′C = C′P : C′A и AP : C′A = CA : C′C. Центр окружности O делит A′A пополам, так что треугольник OAP подобен A′AB и длина OP равна половине длины A′B. В результате получаем
c 2 n 2 = ( r + 1 2 c n ) 2 r c 2 n = s n s 2 n . ^ &=left(r+ >c_
ight)2rc_ &= > >>.end >>
В первом равенстве отрезок C′P равен сумме C′O+OP, что равно r+ 1 ⁄2cn, а отрезок C′C является диаметром и его длина равна 2r. Для единичного круга получаем знаменитую формулу удвоения Людольфа Ван Цейлена
c 2 n = 2 + c n . = >>.>
Если мы теперь построим правильный описанный n-угольник со стороной ″B″, параллельной AB, то OAB и OA″B″ являются подобными с отношением подобия A″B″ : AB = OC : OP. Обозначим описанную сторону Sn, тогда отношение превращается в Sn : sn = 1 : 1 ⁄2cn. (Мы снова используем факт, что OP равен половине A′B.) Получаем
c n = 2 s n S n . =2 > >>.>
Обозначим периметр вписанного многоугольника через un = nsn, а описанного через Un = nSn. Комбинируя равенства, получим
c 2 n = s n s 2 n = 2 s 2 n S 2 n , = > >>=2 > >>,>
u 2 n 2 = u n U 2 n . ^ =u_ U_ .>
Можно также вывести
2 s 2 n S 2 n s n s 2 n = 2 + 2 s n S n , > >> > >>=2+2 > >>,>
2 U 2 n = 1 u n + 1 U n . >>= >>+ >>.>
Видео:Площадь кругаСкачать

Аппроксимация случайными бросаниями [ править | править код ]
Если более эффективные методы недоступны, можно прибегнуть к «бросанию дротиков». Этот метод Монте-Карло использует факт, что при случайных бросаниях точки равномерно распространяются по площади квадрата, в котором расположен круг, число попаданий в круг приближается к отношению площади круга на площадь квадрата. Следует принимать этот метод как последнюю возможность вычисления площади круга (или фигуры любой формы), поскольку для получения приемлемой точности требует огромного числа испытаний. Для получения точности 10 −n необходимо около 100 n случайных испытаний [8] .
Видео:Вот как получили пи эр в квадратеСкачать

Конечная перегруппировка [ править | править код ]
Как мы видели, разбив диск на бесконечное число кусков мы можем из них затем собрать прямоугольник. Интересный факт был открыт относительно недавно Лацковичем [9] , что мы можем разбить круг на большое, однако конечное число кусков, а затем перегруппировать их в квадрат той же площади. Сам вопрос о таком конечном разбиении носит название «Квадратура круга Тарского».
Видео:9 класс, 27 урок, Площадь кругаСкачать

Обобщения [ править | править код ]
Мы можем растянуть круг до формы эллипса. Поскольку это растяжение является линейным преобразованием плокости, оно изменяет площадь, но сохраняет отношения площадей. Этот факт можно использовать для вычисления площади произвольного эллипса, отталкиваясь от площади круга.
Пусть единичный эллипс описан квадратом со стороной 2. Преобразование переводит круг в эллипс путём сжатия или растяжения горизонтального и вертикального диаметров до малой и большой оси эллипса. Квадрат становится прямоугольником, описанным вокруг эллипса. Отношение площади круга к площади квадрата равно π /4, и отношение площади эллипса к площади прямоугольника будет тоже π /4. Если a и b — длины малой и большой осей эллипса. Площадь прямоугольника будет равна ab, а тогда площадь эллипса — π ab/4.
Мы можем распространить аналогичные техники и на большие размерности. Например, если мы хотим вычислить объём внутри сферы, и мы знаем формулу для площади сферы, мы можем использовать приём, аналогичный «луковичному» подходу для круга.
📹 Видео
Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Длина окружности. Математика 6 класс.Скачать

КАК НАЙТИ ПЛОЩАДЬ КРУГА, ОПИСАННОГО ОКОЛО КВАДРАТА? Примеры | ГЕОМЕТРИЯ 9 классСкачать

Площадь круга. Практическая часть - решение задачи. 6 класс.Скачать
Длина окружности. Площадь круга.Скачать

Крутая задача про площадь круга в квадратах. #математика #геометрия #круг #площадь #квадратСкачать

Площадь круга через интегралСкачать

КАК НАЙТИ ПЛОЩАДЬ КРУГА, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР? Примеры | МАТЕМАТИКА 6 классСкачать








