Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.
- Нормальный вектор плоскости – определение, примеры, иллюстрации
- Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
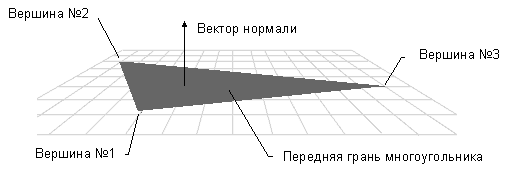
- Вектор нормали к грани
- Вывод четырехугольников
- Лицевые и нелицевые стороны грани
- Интерполяция цветов вершин грани
- Заливка грани по образцу
- Наложение текстуры
- Программная генерация образа
- Загрузка образа из BMP-файла
- Вывод 3d-объекта
- Модель параболоида вращения
- Отсечение невидимых граней
- Использование материалов
- Отображение нормалей
- Заключение
- Приложение 1. Файл GLUtilsMod.f90 с функцией CreateOpenGLWindow
- Приложение 2. Файл GLWinMain.f90 с функцией WinMain
- Приложение 3. Функции WindowProc файла GLMod.f90
- Приложение 4. Вкладка Solution окна проекта Visual Studio
- Вектор нормали к грани
- 🎥 Видео
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Нормальный вектор плоскости – определение, примеры, иллюстрации
Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.
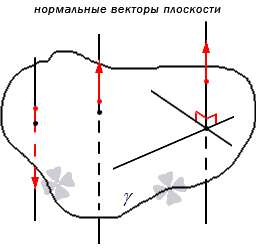
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.
Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.
Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.
Рассмотрим на примере нормального вектора на плоскости.
Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .
Видео:Направляющий и нормальный вектор прямой на плоскости | Векторная алгебраСкачать

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.
Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .
По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.
Ответ: n → = ( 2 , — 3 , 7 ) .
Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .
По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .
Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .
При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .
Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.
Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Вектор нормали к грани
3d-фигуры могут быть созданы в OpenGL как полигональные объекты (рис. 1).
Рис. 1. Полигональное представление сферы, тора и усеченного конуса
В качестве полигона, или грани, наиболее часто берется четырехугольник или треугольник.
В работе рассматриваются примеры, иллюстрирующие некоторые средства OpenGL, позволяющие создавать полигональные объекты и управлять их свойствами.
Все примеры реализованы на Intel-Фортране. При запуске примера реализующий его код помещается в 3 следующие файла:
Файл GLUtilsMod.f90 содержит функцию CreateOpenGLWindow создания окна вывода графических данных и одинаков во всех примерах. Код, записанный в этом файле, приведен в прил. 1.
Файл GLWinMain.f90 содержит функцию WinMain, код которой также одинаков во всех примерах. Он приведен в прил. 2.
Файл GLMod.f90 содержит функцию WindowProc, отвечающую за обработку сообщений. Код этой функции одинаков во всех примерах. Он приведен в прил. 3.
Также файл GLMod.f90 содержит подпрограмму Display и иные процедуры, необходимые для демонстрации примера. Код этих процедур приводится по ходу изложения материала.
Рисунок, показывающий эти файлы в Visual Studio, приведен в прил. 4.
Каждый раз задается белый цвет фона окна вывода:
call fglClearColor(1.0, 1.0, 1.0, 1.0) ! Белый цвет фона
call fglClear(GL_COLOR_BUFFER_BIT) ! Очистка буфера цвета
Во всех случаях применяется прямоугольное проецирование:
call fglOrtho(-w8, w8, -h8, h8, -w8, w8)
Перед вызовом fglOrtho текущей устанавливается единичная матрица проецирования:
call fglMatrixMode(GL_PROJECTION)
call fglLoadIdentity
В функции WinMain задана двойная буферизация (PFD_DOUBLEBUFFER), поэтому после выполнения
call fglFlush ! Вывод в буфер-накопитель
данные попадают во внеэкранный буфер и отображаются в окне вывода только после выполнения
bret = SwapBuffers(hDC) ! Переброска данных в буфер кадра
Имена наиболее значимых для текущего примера процедур выделяются в приводимом коде полужирным шрифтом.
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Вывод четырехугольников
Четырехугольники (GL_QUADS) выводятся в результате указания координат их вершин (используется одна из fglVertex-команд). Координаты вершин перечисляются между командами fglBegin и fglEnd. Вершины одного четырехугольника в нижеследующем примере обходятся против часовой стрелки, а второго — по часовой стрелке. В этом случае по умолчанию наблюдаемая сторона первого полигона является лицевой, а второго — нелицевой.
Пример. Выводятся два прямоугольника (рис. 2). Вершины левого прямоугольника обходятся против часовой стрелки, а правого — по часовой стрелке. Первый прямоугольник заливается красным цветом, а второй — черным.
Рис. 2. Красный и черный прямоугольники
Результат обеспечивает следующий код:
! GLMod.f90
module glMod
use IFWINA
use IFOPNGL
use GLUtilsMod ! См. прил. 1
implicit none
private
public :: hdc, Display, WindowProc
integer(HANDLE) :: hDC ! Контекст устройства
logical(4) rtt
contains
integer(LONG) function WindowProc(hWnd, uMsg, wParam, lParam)
! Приведена в прил. 3
end function WindowProc
!
subroutine display ! Выводит красный и черный прямоугольники
integer(BOOL) :: bret
real(8) :: w8 = 210, h8 = 60
real(4), parameter :: x = 200, y = 50, x2 = 10, z = 0
! Массивы координат вершин прямоугольников
real(4), dimension(3) :: v11(3) = (/-x, -y, z/), v12 = (/-x2, -y, z/), &
v13 = (/-x2, y, z/), v14 = (/-x, y, z/)
real(4), dimension(3) :: v21 = (/x2, -y, z/), v22 = (/x, -y, z/), &
v23 = (/x, y, z/), v24 = (/x2, y, z/)
call fglClearColor(1.0, 1.0, 1.0, 1.0) ! Белый цвет фона
callfglClear(GL_COLOR_BUFFER_BIT) ! Очистка буфера цвета
call fglShadeModel(gl_flat) ! Отказ от интерполяции цветов (GL_FLAT)
call fglMatrixMode(GL_PROJECTION) ! Текущей стала матрица проецирования (GL_PROJECTION)
call fglLoadIdentity ! Инициализация матрицы проецирования
call fglOrtho(-w8, w8, -h8, h8, -w8, w8) ! Область вывода
call fglPolygonMode(GL_FRONT_AND_BACK, GL_FILL) ! Заливка (GL_FILL) полигонов
call fglBegin(GL_QUADS) ! Вывод независимых (GL_QUADS) четырехугольников
! Красный прямоугольник
call fglColor3f(1.0, 0.0, 0.0) ! Текущий цвет красный
call fglVertex3fv (loc(v11)) ! Вершины красного прямоугольника
call fglVertex3fv (loc(v12))
call fglVertex3fv (loc(v13))
call fglVertex3fv (loc(v14))
! Черный прямоугольник
call fglColor3f(0.0, 0.0, 0.0) ! Текущий цвет черный
call fglVertex3fv(loc(v21)) ! Вершины черного прямоугольника
call fglVertex3fv(loc(v22))
call fglVertex3fv(loc(v23))
call fglVertex3fv(loc(v24))
call fglEnd
call fglFlush ! Вывод в буфер-накопитель
bret = SwapBuffers(hDC) ! Переброска данных в буфер кадра
end subroutine display
end module glMod
call fglPolygonMode(GL_FRONT_AND_BACK, GL_FILL)
обеспечивает заливку (GL_FILL ) текущим цветом как лицевой (GL_FRONT), так и нелицевой (GL_BACK) сторон выводимых граней.
Будут выведены только границы (GL_LINE) грани, если употребить
call fglPolygonMode(gl_front_and_back, GL_LINE)
Толщина линии изменяется командой
call fglLineWidth(3.0) ! Толщина линии 3 пикселя (по умолчанию 1 пиксель)
Будут показаны только вершины (GL_POINT) полигона, если задать
call fglPolygonMode(gl_front_and_back, GL_POINT)
Размер точки, отображающей вершину, задается командой
call fglPointSize(8.0) ! Точка в 8 пикселей (по умолчанию берется 1 пиксель)
Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

Лицевые и нелицевые стороны грани
В примере вершины левого прямоугольник обходятся против часовой стрелки, а правого — по часовой стрелке. Поэтому первый прямоугольник является нам лицевой стороной, а правый — нелицевой (рис. 3, а). Способ вывода лицевой стороны GL_POINT, а нелицевой GL_LINE. После нажатия на клавишу «r» прямоугольники поворачиваются на 180° вокруг оси Х, являя нам свои другие стороны(рис. 3, б).
Рис. 3. Лицевые и нелицевые стороны: а — лицевая слева, нелицевая справа; б — нелицевая слева, лицевая справа
Поворот прямоугольников выполняется командой fglRotatef в мировой системе координат, поскольку предварительно текущей устанавливается видовая матрица (GL_MODELVIEW).
Результат обеспечивает следующий код:
! GLMod.f90
module glMod
use IFWINA
use IFOPNGL
use GLUtilsMod ! См. прил. 1
implicit none
private
public :: rtt, hdc, Display, WindowProc
logical :: rtt = .false.
integer(HANDLE) :: hDC ! Контекст устройства
logical(4) rtt
contains
integer(LONG) function WindowProc(hWnd, uMsg, wParam, lParam)
! Приведена в прил. 3
end function WindowProc
!
subroutine display ! Показывает лицевую и нелицевую стороны граней
integer(BOOL) :: bret
real(8) :: w8 = 210, h8 = 60
real(4), parameter :: x = 200, y = 50, x2 = 10, z = 0
! Массивы координат вершин прямоугольников
real(4), dimension(3) :: v11(3) = (/-x, -y, z/), v12 = (/-x2, -y, z/), &
v13 = (/-x2, y, z/), v14 = (/-x, y, z/)
real(4), dimension(3) :: v21 = (/x2, -y, z/), v22 = (/x, -y, z/), &
v23 = (/x, y, z/), v24 = (/x2, y, z/)
call fglClearColor(1.0, 1.0, 1.0, 1.0) ! Белый цвет фона
call fglClear(gl_color_buffer_bit) ! Очистка буфера цвета
call fglShadeModel(gl_flat) ! Отказ от интерполяции цветов (GL_FLAT)
call fglMatrixMode(gl_projection) ! Текущей стала матрица проецирования
call fglLoadIdentity ! Инициализация матрицы проецирования
call fglOrtho(-w8, w8, -h8, h8, -w8, w8) ! Область вывода
call fglPointSize(8.0) ! Размер точки равен 8-и пикселям
call fglLineWidth(2.0) ! Ширина линии равна 2-м пикселям
call fglPolygonMode(GL_FRONT, GL_POINT) ! Выводим лицевую сторону в виде точек на месте вершин
call fglPolygonMode(GL_BACK, GL_LINE) ! Выводим нелицевую сторону в виде линий
call fglMatrixMode(GL_MODELVIEW) ! Текущей стала видовая матрица (GL_MODELVIEW)
! Поворот прямоугольников вокруг оси Х на 180 градусов при каждом нажатии на клавишу «r»
if (rtt) call fglRotatef(180.0, 1.0, 0.0, 0.0) ! См. функцию WindowProc
call fglColor3f(1.0, 0.0, 0.0) ! Текущий цвет красный
call fglBegin(gl_quads) ! Вывод независимых четырехугольников
! Вывод лицевой стороны первого прямоугольника. Вершины обходятся против часовой стрелки
call fglVertex3fv(loc(v11))
call fglVertex3fv(loc(v12))
call fglVertex3fv(loc(v13))
call fglVertex3fv(loc(v14))
! Вывод нелицевой стороны второго прямоугольника. Вершины обходятся по часовой стрелке
call fglVertex3fv(loc(v21))
call fglVertex3fv(loc(v24))
call fglVertex3fv(loc(v23))
call fglVertex3fv(loc(v22))
call fglEnd
call fglFlush ! Вывод в буфер-накопитель
rtt = .false. ! Запрещаем вращение
bret = SwapBuffers(hDC) ! Переброска данных в буфер кадра
end subroutine display
end module glMod
Видео:Вектор нормали к поверхности поля в точкеСкачать

Интерполяция цветов вершин грани
Цвет грани, если не используются материалы, определяется цветом ее вершин, задаваемым fglColor-командой. Каждой вершине может быть назначен свой цвет. В этом случае возможны два следующих варианта:
- интерполяция цветов вершин: fglShadeModel(GL_SMOOTH); выполняется линейная интерполяция цветов;
- отказ от интерполяции цветов вершин: fglShadeModel(GL_FLAT); цвет полигона определяется цветом его последней выведенной вершины.
В примере выводятся два прямоугольника, причем каждой вершине назначается свой цвет. При этом левый прямоугольник (рис. 4) выводится с интерполяцией цветов вершин, а правый — без интерполяции цветов вершин.
Рис. 4. Вывод с GL_SMOOTH (слева) и с GL_FLAT (справа)
Результат обеспечивает следующий код:
Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

Заливка грани по образцу
Грань может быть залита с по образцу. В качестве такового используется битовый образ размера 32*32 бита. При употреблении образца текущим или рассчитанным цветом заливаются те пиксели грани, которым отвечают единичным битам образа. Пиксели, отвечающие нулевым битам образа, закрашиваются цветом фона.
В программе битовый образец хранится массивом, имеющим размер 128 и тип INTEGER(1). Число бит, хранимых массивом, равно 128*8 = 32*32.
Рассмотрим модуль PTTRN, содержащий определение используемого для задания образца массива mask.
module PTTRN integer(1), dimension(128) :: mask = (/ &
#00, #00, #00, #00, #00, #00, #00, #00, #03, #80, #01, #c0, #06, #c0, #03, #60, &
#04, #60, #06, #20, #04, #30, #0c, #20, #04, #18, #18, #20, #04, #0c, #30, #20, &
#04, #06, #60, #20, #44, #03, #c0, #22, #44, #01, #80, #22, #44, #01, #80, #22, &
#44, #01, #80, #22, #44, #01, #80, #22, #44, #01, #80, #22, #44, #01, #80, #22, &
#66, #01, #80, #66, #33, #01, #80, #cc, #19, #81, #81, #98, #0c, #c1, #83, #30, &
#07, #e1, #87, #e0, #03, #3f, #fc, #c0, #03, #31, #8c, #c0, #03, #33, #cc, #c0, &
#06, #64, #26, #60, #0c, #cc, #33, #30, #18, #cc, #33, #18, #10, #c4, #23, #08, &
#10, #63, #c6, #08, #10, #30, #0c, #08, #10, #18, #18, #08, #10, #00, #00, #08 /)
end module PTTRN
Такое заполнение массива отвечает приведенному на рис. 5 образцу.
Рис. 5. Образец, хранимый массивом mask
Образец можно наглядно воспроизвести, если каждые четыре элемента массива mask расположить на одной строке листа, записав эти элементы в двоичном коде и заменив нули пробелами. На рис. 6 показаны таким образом 10 нижних строк образа. Справа в каждой строке записаны отвечающие этой строке элементы массива mask.
Рис. 6. Двоичное представление нижней части образца
В примере с использованием образца mask выводятся два прямоугольника (рис. 7). Первый рисуется с интерполяцией цветов, а второй — без нее.
Рис. 7. Заливка по образцу с интерполяцией цветов и без нее
Для получения результата в код файла GLMod.f90 добавлены определение модуля PTTRN, подключение этого модуля в glMod:
и команды, обеспечивающие заливку по образцу:
call fglPolygonStipple(loc(mask)) ! Задаем образец
call fglEnable(GL_POLYGON_STIPPLE) ! Разрешаем использование образца
Таким образом, имеем следующий файл GLMod.f90:
! GLMod.f90
module PTTRN
integer(1), dimension(128) :: mask = (/ &
#00, #00, #00, #00, #00, #00, #00, #00, #03, #80, #01, #c0, #06, #c0, #03, #60, &
#04, #60, #06, #20, #04, #30, #0c, #20, #04, #18, #18, #20, #04, #0c, #30, #20, &
#04, #06, #60, #20, #44, #03, #c0, #22, #44, #01, #80, #22, #44, #01, #80, #22, &
#44, #01, #80, #22, #44, #01, #80, #22, #44, #01, #80, #22, #44, #01, #80, #22, &
#66, #01, #80, #66, #33, #01, #80, #cc, #19, #81, #81, #98, #0c, #c1, #83, #30, &
#07, #e1, #87, #e0, #03, #3f, #fc, #c0, #03, #31, #8c, #c0, #03, #33, #cc, #c0, &
#06, #64, #26, #60, #0c, #cc, #33, #30, #18, #cc, #33, #18, #10, #c4, #23, #08, &
#10, #63, #c6, #08, #10, #30, #0c, #08, #10, #18, #18, #08, #10, #00, #00, #08 /)
end module PTTRN
!
module glMod
use IFWINA
use IFOPNGL
use GLUtilsMod ! См. прил. 1
use PTTRN
implicit none
private
public :: hdc, Display, WindowProc
integer(HANDLE) :: hDC ! Контекст устройства
logical(4) rtt
contains
integer(LONG) function WindowProc(hWnd, uMsg, wParam, lParam)
! Приведена в прил. 3
end function WindowProc
!
subroutine display ! Заливка прямоугольников по образцу размера 32*32 бита
integer(BOOL) :: bret
real(8) :: w8 = 210, h8 = 60
real(4), parameter :: x = 200, y = 50, x2 = 10, z = 0
! Массивы координат вершин прямоугольников
real(4), dimension(3) :: v11(3) = (/-x, -y, z/), v12 = (/-x2, -y, z/), &
v13 = (/-x2, y, z/), v14 = (/-x, y, z/)
real(4), dimension(3) :: v21 = (/x2, -y, z/), v22 = (/x, -y, z/), &
v23 = (/x, y, z/), v24 = (/x2, y, z/)
call fglClearColor(1.0, 1.0, 1.0, 1.0) ! Белый цвет фона
call fglClear(gl_color_buffer_bit) ! Очистка буфера цвета
call fglMatrixMode(gl_projection) ! Текущей стала матрица проецирования
call fglLoadIdentity ! Инициализация матрицы проецирования
call fglOrtho(-w8, w8, -h8, h8, -w8, w8) ! Область вывода
call fglPolygonMode(gl_front_and_back, gl_fill) ! Заливка полигонов
call fglPolygonStipple(loc(mask)) ! Задаем образец
call fglEnable(GL_POLYGON_STIPPLE) ! Разрешаем использование образца
call fglShadeModel(gl_smooth) ! Употребляем интерполяцию цветов
call fglBegin(gl_quads)
call fglColor3f(0.0, 1.0, 0.0) ! Текущий цвет зеленый
call fglVertex3fv(loc(v11))
call fglColor3f(0.0, 0.0, 1.0) ! Текущий цвет синий
call fglVertex3fv(loc(v12))
call fglColor3f(1.0, 1.0, 0.0) ! Текущий цвет желтый
call fglVertex3fv(loc(v13))
call fglColor3f(1.0, 0.0, 0.0) ! Текущий цвет красный
call fglVertex3fv(loc(v14))
call fglEnd
call fglShadeModel(gl_flat) ! Вывод без интерполяции цветов (текущий цвет красный)
call fglBegin(gl_quads)
call fglVertex3fv(loc(v21))
call fglVertex3fv(loc(v22))
call fglVertex3fv(loc(v23))
call fglVertex3fv(loc(v24))
call fglEnd
call fglFlush ! Вывод в буфер-накопитель
bret = SwapBuffers(hDC) ! Переброска данных в буфер кадра
end subroutine display
end module glMod
Видео:Уравнение плоскости через точку и нормальСкачать

Наложение текстуры
Образ, хранимый текстурой, накладывается на выводимую грань с учетом координат текстуры и ее параметров. Координаты текстуры отвечают за повторяемость образа на выводимом изображении, что иллюстрирует рис. 8, при выводе которого употреблена 2d-текстура с координатами (2.0, 2.0) для левого прямоугольника и с координатами (1.0, 1.0) для правого прямоугольника.
Рис. 8. Текстурированные прямоугольники. Слева координаты текстуры (2.0, 2.0), а справа — (1.0, 1.0)
RGB-компоненты образа для текстуры в приводимых ниже программах хранит массив image(3, iWidth, iHeight). При работе с текстурой использованы следующие ограничения:
- берется 2d-текстура;
- используется текстура с данными типа GL_UNSIGNED_BYTE (вмещает диапазон 0 — 255);
- каждый элемент текстуры содержит три компонента (формат текстуры GL_RGB);
- размеры массивы image есть число 2n;
- размеры текстуры есть число 2n;
- в случае загрузки образ может быть взят только из 24-разрядного BMP-файла.
Программная генерация образа
Программно создается показанный на рис. 9 образ.
Рис. 9. Генерируемый образ
Для его генерации использована следующая подпрограмма:
subroutine makeImg
allocate(image(3, iWidth, iHeight))
image = 255 ! Инициализация образа белым цветом (255, 255, 255)
! Корректировка цвета образа
image(1:2, 1:16, 17:32) = 0 ! (0, 0, 255)
image(2:3, 1:16, 49:64) = 0 ! (255, 0, 0)
image(1, 17:32, 1:16) = 0 ! (0, 255, 255)
image(2, 17:32, 32:48) = 0 ! (255, 0, 255)
image(3, 32:48, 17:32) = 0 ! (255, 255, 0)
image(1, 32:48, 49:64) = 0 ! (0, 255, 255)
image(3, 32:48, 49:64) = 0 ! (0, 255, 0)
image(1:2, 49:64, 1:16) = 100 ! (100, 100, 255)
image(2:3, 49:64, 32:48) = 100 ! (255, 100, 100)
end subroutine makeImg
Первоначально массив image заполняется данными, отвечающими белому цвету. Затем в массиве берутся элементы, соответствующие квадратной части образа, и меняются значения, отвечающие или R, или G, или B-компоненте цвета. В двух последних строках подпрограммы makeImg изменяются значения двух компонент цвета. Получаемый цвет взятой квадратной части показан в коде в строке комментария.
В случае черно-белой текстуры такой же образ можно создать (рис. 10), употребив следующий код:
subroutine makeImg
integer(4) i, j
allocate(image(3, iWidth, iHeight))
do i = 1, iHeight ! Генерация черно-белого образа, на основе которого создается текстура
do j = 1, iWidth
image(:, i, j) = ieor(iand(i — 1, 16), iand(j — 1, 16)) * 255
end do
end do
end subroutine makeImg
Рис. 10. Черно-белый образ
После генерации образ употребляется в команде
call fglTexImage2D(GL_TEXTURE_2D, 0, 3, iWidth, iHeight, 0, GL_RGB, GL_UNSIGNED_BYTE, loc(image)),
создающей 2d-текстуру размера iWidth*iHeight.
Порядок ее наложения на грань регулируется параметрами текстуры и способом ее взаимодействия с текущим фрагментом изображения (команды fglTexParameterf и fglTexEnvf).
Текстура будет использована, если задана команда
Получение приведенного на рис. 8 изображения обеспечивает следующий код, в котором генерацию и инициализацию текстуры обеспечивает подпрограмма texInit:
! GLMod.f90
module glMod
use IFWINA
use IFOPNGL
use GLUtilsMod ! См. прил. 1
implicit none
private
public :: hdc, Display, WindowProc, image
integer(HANDLE) :: hDC ! Контекст устройства
logical(4) rtt
integer(1), allocatable :: image(:, :, 🙂 ! Образ текстуры
contains
integer(LONG) function WindowProc(hWnd, uMsg, wParam, lParam)
! Приведена в прил. 3
end function WindowProc
!
subroutine display ! Выводит 2 текстурированных прямоугольника
integer(BOOL) :: bret
real(8) :: w8 = 210, h8 = 60
real(4), parameter :: x = 200, y = 50, x2 = 10, z = 0
! Массивы координат вершин прямоугольников
real(4), dimension(3) :: v11(3) = (/-x, -y, z/), v12 = (/-x2, -y, z/), &
v13 = (/-x2, y, z/), v14 = (/-x, y, z/)
real(4), dimension(3) :: v21 = (/x2, -y, z/), v22 = (/x, -y, z/), &
v23 = (/x, y, z/), v24 = (/x2, y, z/)
real(4) :: tci = 0.0, tca ! Координаты текстуры
call fglClearColor(1.0, 1.0, 1.0, 1.0) ! Белый цвет фона
call fglClear(gl_color_buffer_bit) ! Очистка буфера цвета
call fglMatrixMode(gl_projection) ! Текущей стала матрица проецирования
call fglLoadIdentity ! Инициализация матрицы проецирования
call fglOrtho(-w8, w8, -h8, h8, -w8, w8) ! Область вывода
call fglPolygonMode(gl_front_and_back, gl_fill) ! Заливка полигонов
call texInit ! Генерация образа и создание текстуры
call fglBegin(gl_quads)
! Координаты текстуры и вершин левого прямоугольника
tca = 2.0
call fglTexCoord2f(tci, tci)
call fglVertex3fv(loc(v11))
call fglTexCoord2f(tci, tca)
call fglVertex3fv(loc(v12))
call fglTexCoord2f(tca, tca)
call fglVertex3fv(loc(v13))
call fglTexCoord2f(tca, tci)
call fglVertex3fv(loc(v14))
! Координаты текстуры и вершин правого прямоугольника
tca = 1.0
call fglTexCoord2f(tci, tci)
call fglVertex3fv(loc(v21))
call fglTexCoord2f(tci, tca)
call fglVertex3fv(loc(v22))
call fglTexCoord2f(tca, tca)
call fglVertex3fv(loc(v23))
call fglTexCoord2f(tca, tci)
call fglVertex3fv(loc(v24))
call fglEnd
call fglFlush ! Вывод в буфер-накопитель
bret = SwapBuffers(hDC) ! Переброска данных в буфер кадра
end subroutine display
end module glMod
!
subroutine texInit ! Генерирует образ и создает текстуру
use glMod
use IFOPNGL
implicit none
integer(4), parameter :: iWidth = 64, iHeight = 64
! Размер текстуры равен iWidth * iHeight
! Каждый элемент текстуры содержит три компонента (формат текстуры GL_RGB)
! Тип GL_UNSIGNED_BYTE вмещает диапазон 0 — 255, поэтому тип INTEGER(1) задается для образа image текстуры
if(.not. allocated(image)) then
call makeImg ! Создаем образ для текстуры
! Создаем 2d-текстуру на основе образа image
call fglTexImage2D(GL_TEXTURE_2D, 0, 3, iWidth, iHeight, 0, GL_RGB, GL_UNSIGNED_BYTE, loc(image))
! Задаем параметры текстуры
call fglTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT)
call fglTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT)
call fglTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR)
call fglTexParameterf(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR)
! Способ взаимодействия с текущим фрагментом изображения
call fglTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_DECAL)
! Разрешаем употребление текстуры
call fglEnable(GL_TEXTURE_2D)
end if
contains
subroutine makeImg
allocate(image(3, iWidth, iHeight))
image = 255 ! Инициализация образа белым цветом (255, 255, 255)
! Корректировка цвета образа
image(1:2, 1:16, 17:32) = 0 ! (0, 0, 255)
image(2:3, 1:16, 49:64) = 0 ! (255, 0, 0)
image(1, 17:32, 1:16) = 0 ! (0, 255, 255)
image(2, 17:32, 32:48) = 0 ! (255, 0, 255)
image(3, 32:48, 17:32) = 0 ! (255, 255, 0)
image(1, 32:48, 49:64) = 0 ! (0, 255, 255)
image(3, 32:48, 49:64) = 0 ! (255, 255, 0)
image(1:2, 49:64, 1:16) = 100 ! (100, 100, 255)
image(2:3, 49:64, 32:48) = 100 ! (255, 100, 100)
end subroutine makeImg
end subroutine texInit
Загрузка образа из BMP-файла
Рассматривается пример, в котором растровые данные образа берутся непосредственно из 24-разрядного BMP-файла.
В начале BMP-файла располагаются сведения о типе файла и параметрах хранимого им рисунка. Прочитать эти данные можно с помощью переменных производного типа T_BitMapFileHeader и BitMapInfoHeader. Эти типы описаны в файле IFWINTY.f90:
type T_BitMapFileHeader
character(2) :: bfType ! Тип файла — символы BM
integer(4) :: bfSize ! Размер файла
integer(4) :: bfReserved1 ! Зарезервированное поле
integer(4) :: bfReserved2 ! Зарезервированное поле
integer(4) :: bfOffBits ! Расстояние в байтах от начала файла до растровых данных
end type T_BitMapFileHeader !
!
type T_BitMapInfoHeader
integer(4) :: biSize ! Размер заголовка изображения (40 байт)
integer(4) :: biWidth ! Ширина рисунка в пикселях
integer(4) :: biHeight ! Высота рисунка в пикселях
integer(2) :: biPlanes ! Количество плоскостей рисунка (1)
integer(2) :: biBitCount ! Количество бит в пикселе
integer(4) :: biCompression ! Применяется ли сжатие (0, если не применяется)
integer(4) :: biSizeImage ! Размер образа в байтах
integer(4) :: biXPelsPerMeter ! Вертикальное разрешение в пикселях на метр
integer(4) :: biYPelsPerMeter ! Горизонтальное разрешение в пикселях на метр
integer(4) :: biClrUsed ! Количество индексов цвета в таблице цветов
integer(4) :: biClrImportant ! Количество индексов цвета в таблице цветов, которое необходимо для вывода рисунка
end type T_BitMapInfoHeader
Приводимая ниже подпрограмма loadImg читает заголовок указанного файла (в примере читается файл ct256.bmp). Проверяет, является ли этот файл 24-разрядным, и в случае положительно результата переносит растровые данные сначала в массив temp, а затем в массив image, адрес которого подается на вход команды fglTexImage2D:
call fglTexImage2D(gl_texture_2d, 0, 3, iWidth, iHeight, 0, gl_rgb, gl_unsigned_byte, loc(image))
Размеры текстуры задаются равными размерам растрового образа, которые, напомним, есть целая степень числа 2.
В примере размеры текстуры и образа, хранимого BMP-файлом, одинаковы и равны 256*256.
Если размеры текстуры и растрового образа различны, то употребляется команда
ios = fgluScaleImage(gl_rgb, iWidth, iHeight, gl_unsigned_byte, image, iWidth2, iHeight2, gl_unsigned_byte, sdata)
которая принимает образ image размера iWidth*iHeight и возвращает образ sdata размера iWidth2*iHeight2. Последний подается затем команде
call fglTexImage2D(gl_texture_2d, 0, 3, iWidth2, iHeight2, 0, gl_rgb, gl_unsigned_byte, loc(sdata))
Массив sdata имеет тип INTEGER(1) и форму (3, iHeight2, iWidth2)
Возможный результат текстурирования двух прямоугольников показан на рис. 11.
Рис. 11. Текстура из BMP-файла. Слева координаты текстуры (2.0, 2.0), а справа — (1.0, 1.0)
Если файл не найден или если разрядность данных отличается от 24, то подпрограммой badImg формируется черная текстура с размерами 64*64.
Результат обеспечивает следующий код:
! GLMod.f90
module glMod
use IFWINA
use IFOPNGL
use GLUtilsMod ! См. прил. 1
implicit none
private
public :: hdc, Display, WindowProc, image
integer(HANDLE) :: hDC ! Контекст устройства
logical(4) rtt
integer(1), allocatable :: image(:, :, 🙂 ! Образ текстуры
contains
integer(LONG) function WindowProc(hWnd, uMsg, wParam, lParam)
! Приведена в прил. 3
end function WindowProc
!
subroutine display ! Выводит 2 текстурированных прямоугольника
integer(BOOL) :: bret
real(8) :: w8 = 210, h8 = 60
real(4), parameter :: x = 200, y = 50, x2 = 10, z = 0
! Массивы координат вершин прямоугольников
real(4), dimension(3) :: v11(3) = (/-x, -y, z/), v12 = (/-x2, -y, z/), &
v13 = (/-x2, y, z/), v14 = (/-x, y, z/)
real(4), dimension(3) :: v21 = (/x2, -y, z/), v22 = (/x, -y, z/), &
v23 = (/x, y, z/), v24 = (/x2, y, z/)
real(4) :: tci = 0.0, tca ! Координаты текстуры
call fglClearColor(1.0, 1.0, 1.0, 1.0) ! Белый цвет фона
call fglClear(gl_color_buffer_bit) ! Очистка буфера цвета
call fglMatrixMode(gl_projection) ! Текущей стала матрица проецирования
call fglLoadIdentity ! Инициализация матрицы проецирования
call fglOrtho(-w8, w8, -h8, h8, -w8, w8) ! Область вывода
call fglPolygonMode(gl_front_and_back, gl_fill) ! Заливка полигонов
call texInitBmp ! Загрузка образа и создание текстуры
call fglBegin(gl_quads)
! Координаты текстуры и вершин левого прямоугольника
tca = 2.0
call fglTexCoord2f(tci, tci)
call fglVertex3fv(loc(v11))
call fglTexCoord2f(tci, tca)
call fglVertex3fv(loc(v12))
call fglTexCoord2f(tca, tca)
call fglVertex3fv(loc(v13))
call fglTexCoord2f(tca, tci)
call fglVertex3fv(loc(v14))
!
! Координаты текстуры и вершин правого прямоугольника
tca = 1.0
call fglTexCoord2f(tci, tci)
call fglVertex3fv(loc(v21))
call fglTexCoord2f(tci, tca)
call fglVertex3fv(loc(v22))
call fglTexCoord2f(tca, tca)
call fglVertex3fv(loc(v23))
call fglTexCoord2f(tca, tci)
call fglVertex3fv(loc(v24))
call fglEnd
call fglFlush ! Вывод в буфер-накопитель
bret = SwapBuffers(hDC) ! Переброска данных в буфер кадра
end subroutine display
end module glMod
!
subroutine texInitBMP ! Загружает данные из BMP-файла и формирует 2d-текстуру
use glMod
use IFOPNGL
use IFOPNGLT
integer(4) iWidth, iHeight
if(.not. allocated(image)) then
call loadImg ! Загружаем из BMP-файла образ для текстуры
! Создаем 2d-текстуру на основе образа image
call fglTexImage2D(gl_texture_2d, 0, 3, iWidth, iHeight, 0, gl_rgb, gl_unsigned_byte, loc(image))
! Задаем параметры текстуры
call fglTexParameterf(gl_texture_2d, gl_texture_wrap_s, gl_repeat)
call fglTexParameterf(gl_texture_2d, gl_texture_wrap_t, gl_repeat)
call fglTexParameterf(gl_texture_2d, gl_texture_mag_filter, gl_linear)
call fglTexParameterf(gl_texture_2d, gl_texture_min_filter, gl_linear)
! Способ нанесения текстуры
call fglTexEnvf(gl_texture_env, gl_texture_env_mode, gl_decal)
! Разрешаем употребление текстуры
call fglEnable(gl_texture_2d)
end if
contains
subroutine loadImg ! Обработка BMP-файла
use IFWINA
implicit none
type(T_BitMapFileHeader) h1
type(T_BitMapInfoHeader) h2
character(20) :: fn = ‘ct256.bmp’
integer(1), allocatable :: temp(:)
integer(4) :: ios, arrSize, i, ii, j
open(1, file = fn, form = ‘binary’, iostat = ios, status = ‘old’)
if(ios /= 0) then ! Проверяем, удалось ли открыть файл
ios = MessageBox(NULL, ‘File ‘ // trim(fn) // ‘ not found’C, «»C, MB_OK)
call badImg
return
end if
read(1) h1, h2
if(h2%biBitCount /= 24) then ! Нужен 24-разрядный файл
ios = MessageBox(NULL, ‘Not 24-bit file’C, «»C, MB_OK)
call badImg
return
end if
arrSize = h2%biSizeImage ! Размер массива TEMP, хранящего растровые данные BMP-файла
allocate(temp(arrSize))
read(1) temp ! Ввод растровых данных в массив TEMP
iWidth = h2%biWidth
iHeight = h2%biHeight
allocate(image(3, iHeight, iWidth))
ii = 0
do i = 1, iHeight
do j = 1, iWidth
image(1, i, j) = temp(ii + 3) ! Компоненты красного, зеленого и синего цвета
image(2, i, j) = temp(ii + 2)
image(3, i, j) = temp(ii + 1)
ii = ii + 3
end do
end do
end subroutine loadImg
!
! Формирует черный образ, если не найден файл или если поданы не 24-разрядные данные
subroutine badImg
iWidth = 64
iHeight = 64
allocate(image(3, iHeight, iWidth))
image = 0 ! (0, 0, 0)
end subroutine badImg
end subroutine texInitBMP
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Вывод 3d-объекта
Модель параболоида вращения
Рассматривается задача вывода параболоида вращения, а точнее его полигонального представления (рис. 12).
Рис. 12. Полигональное представление параболоида y = x 2 + z 2
Для вывода параболоида нужно знать координаты его вершин, а при получении тонового отображения (используется материал и источник света) необходимы сведения о координатах нормалей к граням или вершинам параболоида.
В приводимой ниже программе эти сведения хранит массив vrts производного типа vrtx.
type vrtx ! Тип для задания массивов с координатами вершин и нормалей
real(4) p(3) ! Координаты вершины
real(4) sn(3) ! Координаты внешней нормали к грани; используются при выводе тоновой модели
end type vrtx
type(vrtx), allocatable :: vrts(:, 🙂 ! Массив координат вершин и нормалей
Компонентами типа являются векторы p (3) и sn (3), хранящие соответственно координаты вершины и координаты к грани в текущей вершине.
Для вычисления координат вершин в программе задается высота hcover, число сечений ch параболоида плоскостями y = const, число вершин в сечении. В каждом сечении вершины располагаются в соответствии с рис. 13.
Рис. 13. Вершины в сечении параболоида
Координаты вершин параболоида возвращаются функцией fiVerts, последовательно просматривающей вершины в каждом сечении.
После получения координат вершин подпрограмма norm вычисляет координаты внешней нормали к грани в каждой вершине параболоида и координаты нормали к крышке параболоида.
При выводе грани параболоида ее вершины обходятся против часовой стрелки (рис. 14), поэтому грань предстает перед нами своей внешней стороной.
Рис. 14. Порядок вывода вершин грани
Координаты нормали к грани определяются как векторное произведение векторов, построенных на смежных ребрах грани (рис. 15).
Рис. 15. Вектор внешней нормали к грани
Затем нормали приводятся к единичной длине.
Нормаль к вершине следует вычислять по правилу параллелограмма, то есть как сумму нормалей ко всем граням, которым вершина принадлежит (рис. 16).
Рис. 16. Нормали к граням и вершине
В рассматриваемом примере, однако, таких вычислений не выполняется, и при выводе тоновой модели параболоиде в режиме сглаживания берутся нормали, предоставленные подпрограммой norm.
Отсечение невидимых граней
Если не принять специальных мер, то в режиме GL_LINE вывода полигонов будут показаны все ребра параболоида (рис. 17, а).
Рис. 17. Параболоид: а — выводятся все грани; б — выводятся только видимые грани
В случае выпуклой 3d-фигуры вывод невидимых граней и, следовательно, невидимых ребер (рис. 17, б) можно предотвратить, употребив две следующие команды
call fglCullFace(GL_BACK) ! Запрещен вывод граней, смотрящих на нас нелицевой стороной
call fglEnable(GL_CULL_FACE) ! Активизируем режим GL_CULL_FACE
Поскольку в нашем случае при выводе грани ее вершины обходятся против часовой стрелки, то невидимые грани будут смотреть на нас нелицевой стороной. Этим и объясняется значение GL_BACK, подаваемое команде fglCullFace.
Задачи создания модели параболоида и вывода его граней в режиме GL_LINE решает следующий код:
! GLMod.f90
module paravals ! Данные о параболоиде
integer(4) :: n = 24 ! Число вершин в сечении параболоида
integer(4) :: ch = 7 ! Увеличенное на 1 число сечений параболоида плоскостями y = const
real(4) :: hcover = 20.0 ! Высота параболоида
type vrtx ! Тип для задания массивов вершин и нормалей
real(4) p (3) ! Координаты вершины
real(4) sn (3) ! Координаты внешней нормали к грани; используются при выводе тоновой модели
end type vrtx
type(vrtx), allocatable :: vrts(:, 🙂 ! Массив координат вершин и нормалей
end module paravals
!
module glMod
use IFWINA
use IFOPNGL
use GLUtilsMod ! См. прил. 1
implicit none
private
public :: hdc, Display, WindowProc
integer(HANDLE) :: hDC ! Контекст устройства
logical(4) rtt
contains
integer(LONG) function WindowProc(hWnd, uMsg, wParam, lParam)
! Приведена в прил. 3
end function WindowProc
!
subroutine display ! Выводит полигональную модели параболоида
use paravals
integer(BOOL) :: bret
real(8) :: w8 = 15, h8 = 15
integer(4) i, j, ii, jj
call fglClearColor(1.0, 1.0, 1.0, 1.0) ! Белый цвет фона
! Очистка буфера глубины понадобится в программе вывода закрашенного параболоида
call fglClear(gl_color_buffer_bit)
call fglShadeModel(gl_flat) ! GL_FLAT — нет интерполяции цветов
call fglMatrixMode(gl_projection) ! Текущей стала матрица проецирования
call fglLoadIdentity ! Инициализация матрицы проецирования
call fglOrtho(-w8, w8, -h8, h8, -w8, w8) ! Область вывода
call fglPolygonMode(gl_front_and_back, GL_LINE) ! Вывод ребер
call fglColor3f(0.0, 0.0, 0.0) ! Текущий цвет черный
if(.not. allocated(vrts)) then
call parabInit ! Формируем полигональную модель параболоида
call fglMatrixMode(gl_modelview) ! Теперь текущей является видовая матрица
call fglLoadIdentity ! Инициализация видовой матрицы
call fglRotatef(30.0, 1.0, 0.0, 0.0) ! Поворот относительно оси X
call fglRotatef(-5.0, 0.0, 1.0, 0.0) ! Поворот относительно оси Y
call fglTranslatef(0.0, -10.0, 0.0) ! Перенос объекта вниз (вдоль оси Y)
end if
callfglCullFace(GL_BACK) ! Запрещен вывод граней, смотрящих на нас нелицевой стороной
call fglEnable(GL_CULL_FACE) ! Активизируем режим GL_CULL_FACE
call fglBegin(GL_QUADS) ! Вывод боковых граней параболоида
do i = 1, ch — 1
ii = i + 1
do j = 1, n — 1
jj = j + 1
call fglVertex3f(vrts(i, j)%p(1), vrts(i, j)%p(2), vrts(i, j)%p(3))
call fglVertex3f(vrts(i, jj)%p(1), vrts(i, jj)%p(2), vrts(i, jj)%p(3))
call fglVertex3f(vrts(ii, jj)%p(1), vrts(ii, jj)%p(2), vrts(ii, jj)%p(3))
call fglVertex3f(vrts(ii, j)%p(1), vrts(ii, j)%p(2), vrts(ii, j)%p(3))
end do
j = n; jj = 1
call fglVertex3f(vrts(i, j)%p(1), vrts(i, j)%p(2), vrts(i, j)%p(3))
call fglVertex3f(vrts(i, jj)%p(1), vrts(i, jj)%p(2), vrts(i, jj)%p(3))
call fglVertex3f(vrts(ii, jj)%p(1), vrts(ii, jj)%p(2), vrts(ii, jj)%p(3))
call fglVertex3f(vrts(ii, j)%p(1), vrts(ii, j)%p(2), vrts(ii, j)%p(3))
end do
call fglEnd ! Заканчиваем вывод боковых граней параболоида
call fglBegin(GL_POLYGON) ! Вывод крышки
do i = 1, n
call fglVertex3f(vrts(ch, i)%p(1), vrts(ch, i)%p(2), vrts(ch, i)%p(3))
end do
call fglEnd ! Заканчиваем вывод крышки
call fglFlush ! Вывод в буфер-накопитель
bret = SwapBuffers(hDC) ! Переброска данных в буфер кадра
end subroutine display
end module glMod
!
subroutine parabinit
use paravals
use IFOPNGL
integer i, j
allocate(vrts(ch, n))
vrts = fiVrts() ! Формируем массив вершин
contains
!
function fiVrts ! Возвращает массив вершин
implicit none
type(vrtx) fiVrts(ch, n)
real(4) hp, dh, al, dal
dh = hcover / real(ch — 1) ! Расстояние между сечениями
dal = 4.0 * asin(1.0) / real(n) ! dal — угол между вершинами сечения
hp = dh ! Первое сечение
hp = 0.1 ! Низ параболоида
do i = 1, ch ! Перебор сечений
al = 0.0 ! Первая вершина лежит на оси Х
do j = 1, n ! Перебор вершин сечения
fiVrts(i, j)%p(2) = hp ! Y-координата вершины
fiVrts(i, j)%p(1:3:2) = sqrt(hp) * (/ cos(al), -sin(al) /) ! X и Z-координаты вершины
al = al + dal
end do
hp = hp + dh
end do
end function fiVrts
end subroutine parabinit
Использование материалов
Материалы и источники света дают возможность получать реалистические изображения 3d-объектов.
В общем случае задаются RGBA-значения диффузионного (diffuse) и зеркального (specular) отражения и фонового (ambient) рассеивания и излучения (emission) материала. Эти значения подаются fglMaterial-команде. Аналогичные компоненты имеет и источник света, но в этом случае для их задания употребляется fglLight-команда.
В примере регулируется только одна компонента цвета материала и источника света, а для прочих используются значения по умолчанию.
Создаются два варианта изображения. В первом варианте, когда нормали задаются к граням, команда
call fglNormal3f(vrts(i, j)%sn(1), vrts(i, j)%sn(2), vrts(i, j)%sn(3))
предшествует выводу вершин грани, и поэтому все вершины грани имеют одинаковую нормаль.
Получаемое изображение (рис. 18, а) имеет выраженные цветовые перепады (не поможет и задание GL_SMOOTH-интерполяции цветов).
Рис. 18. Тоновая закраска параболоида: а — все вершины грани имеют одинаковую нормаль; б — вершины грани имеют разные нормали, рассчитанные подпрограммой norm
Для сглаживания цветовых перепадов (рис. 18, б), во-первых, задается GL_SMOOTH-интерполяции цветов, а во-вторых каждой вершине назначается нормаль, определенная подпрограммой norm.
Приводимый далее код, обеспечивает получение рис. 18, а. Изменения, дающие рис. 18, б, описываются ниже.
! GLMod.f90
module paravals ! Данные о параболоиде
integer(4) :: n = 24 ! Число вершин в сечении параболоида
integer(4) :: ch = 7 ! Увеличенное на 1 число сечений параболоида плоскостями y = const
real(4) :: hcover = 20.0 ! Высота параболоида
type vrtx ! Тип для задания массивов вершин и нормалей
real(4) p(3) ! Координаты вершины
real(4) sn(3) ! Координаты внешней нормали к грани; используются при выводе тоновой модели
end type vrtx
type(vrtx), allocatable :: vrts(:, 🙂 ! Массив координат вершин и нормалей
real(4) top(3) ! Координаты нормалей к крышке
end module paravals
!
module glMod
use IFWINA
use IFOPNGL
use GLUtilsMod ! См. прил. 1
implicit none
private
public :: hdc, Display, WindowProc
integer(HANDLE) :: hDC ! Контекст устройства
logical(4) rtt
contains
integer(LONG) function WindowProc(hWnd, uMsg, wParam, lParam)
! Приведена в прил. 3
end function WindowProc
!
subroutine display ! Вывод параболоида с использованием материала
use paravals
integer(BOOL) :: bret
real(8) :: w8 = 15, h8 = 15
integer(4) i, j, ii, jj
! Материал желтого цвета
real(4), dimension(4) :: mtClr = (/ 1.0, 1.0, 0.0, 0.0 /)
! Координаты источника света
real(4), dimension(4) :: light_position = (/ 0.0, 40.0, 40.0, 0.0 /)
! Источник темно-красного света
real(4), dimension(4) :: lghtClr = (/ 0.75, 0., 0., 0.0 /)
call fglClearColor(1.0, 1.0, 1.0, 1.0) ! Белый цвет фона
! Очистка буфера глубины понадобится в программе вывода закрашенного параболоида
call fglClear(gl_color_buffer_bit)
call fglShadeModel(GL_FLAT) ! GL_FLAT — нет интерполяции цветов
call fglMatrixMode(gl_projection) ! Текущей стала матрица проецирования
call fglLoadIdentity ! Инициализация матрицы проецирования
call fglOrtho(-w8, w8, -h8, h8, -w8, w8) ! Область вывода
call fglPolygonMode(gl_front_and_back, gl_fill) ! Заливка полигонов
call fglMaterialfv(GL_FRONT, GL_SPECULAR, loc(mtClr))
call fglLightfv(GL_LIGHT0, GL_POSITION, loc(light_position))
call fglLightfv(GL_LIGHT0, GL_SPECULAR, loc(lghtClr))
call fglEnable(GL_LIGHTING) ! Активизируем заданные параметры освещенности
call fglEnable(GL_LIGHT0) ! Включаем в уравнение освещенности источник GL_LIGHT0
if(.not. allocated(vrts)) then
call parabinit ! Формируем полигональную модель параболоида
call fglMatrixMode(gl_modelview) ! Теперь текущей является видовая матрица
call fglLoadIdentity ! Инициализация видовой матрицы
call fglRotatef(30.0, 1.0, 0.0, 0.0) ! Поворот относительно оси X
call fglRotatef(-5.0, 0.0, 1.0, 0.0) ! Поворот относительно оси Y
call fglTranslatef(0.0, -10.0, 0.0) ! Перенос объекта вниз (вдоль оси Y)
end if
call fglCullFace(GL_BACK) ! Запрещен вывод граней, смотрящих на нас нелицевой стороной
call fglEnable(GL_CULL_FACE) ! Активизируем режим GL_CULL_FACE
call fglBegin(gl_quads) ! Вывод боковых граней
do i = 1, ch — 1
ii = i + 1
do j = 1, n — 1
jj = j + 1
! Задаем нормаль к грани (одна нормаль для всех вершин грани)
call fglNormal3f(vrts(i, j)%sn(1), vrts(i, j)%sn(2), vrts(i, j)%sn(3))
call fglVertex3f(vrts(i, j)%p(1), vrts(i, j)%p(2), vrts(i, j)%p(3))
call fglVertex3f(vrts(i, jj)%p(1), vrts(i, jj)%p(2), vrts(i, jj)%p(3))
call fglVertex3f(vrts(ii, jj)%p(1), vrts(ii, jj)%p(2), vrts(ii, jj)%p(3))
call fglVertex3f(vrts(ii, j)%p(1), vrts(ii, j)%p(2), vrts(ii, j)%p(3))
end do
j = n; jj = 1
! Задаем нормаль к грани (одна нормаль для всех вершин грани)
call fglNormal3f(vrts(i, j)%sn(1), vrts(i, j)%sn(2), vrts(i, j)%sn(3))
call fglVertex3f(vrts(i, j)%p(1), vrts(i, j)%p(2), vrts(i, j)%p(3))
call fglVertex3f(vrts(i, jj)%p(1), vrts(i, jj)%p(2), vrts(i, jj)%p(3))
call fglVertex3f(vrts(ii, jj)%p(1), vrts(ii, jj)%p(2), vrts(ii, jj)%p(3))
call fglVertex3f(vrts(ii, j)%p(1), vrts(ii, j)%p(2), vrts(ii, j)%p(3))
end do
call fglEnd ! Заканчиваем вывод боковых граней
! Задаем нормаль к крышке
call fglBegin(gl_polygon) ! Вывод крышки
call fglNormal3f(top(1), top(2), top(3))
do i = 1, n
call fglVertex3f(vrts(ch, i)%p(1), vrts(ch, i)%p(2), vrts(ch, i)%p(3))
end do
call fglEnd ! Заканчиваем вывод крышки
call fglFlush ! Вывод в буфер-накопитель
bret = SwapBuffers(hDC) ! Переброска данных в буфер кадра
end subroutine display
end module glMod
!
subroutine parabinit
use paravals
use IFOPNGL
integer i, j
allocate(vrts(ch, n))
vrts = fiVrts() ! Формируем массив вершин
call norm ! Рассчитываем нормали к боковым граням и крышке
contains ! Нормали используются при закраске параболоида
!
function fiVrts ! Возвращает массив вершин
implicit none
type(vrtx) fiVrts(ch, n)
real(4) hp, dh, al, dal
dh = hcover / real(ch — 1) ! Расстояние между сечениями
dal = 4.0 * asin(1.0) / real(n) ! dal — угол между вершинами сечения
hp = dh ! Первое сечение
hp = 0.1 ! Низ параболоида
do i = 1, ch ! Перебор сечений
al = 0.0 ! Первая вершина лежит на оси Х
do j = 1, n ! Перебор вершин сечения
fiVrts(i, j)%p(2) = hp ! Y-координата вершины
fiVrts(i, j)%p(1:3:2) = sqrt(hp) * (/ cos(al), -sin(al) /) ! X и Z-координаты вершины
al = al + dal
end do
hp = hp + dh
end do
end function fiVrts
!
subroutine norm ! Формируем нормали к граням
real(8) a(3), b(3) ! Массивы координат векторов a и b
do i = 1, ch — 1
do j = 1, n — 1
a = vrts(i, j + 1)%p — vrts(i, j)%p
b = vrts(i + 1, j)%p — vrts(i, j)%p
vrts(i, j)%sn(1) = a(2)*b(3) — b(2)*a(3) ! Координаты вектора внешней нормали к боковой грани
vrts(i, j)%sn(2) = a(3)*b(1) — b(3)*a(1)
vrts(i, j)%sn(3) = a(1)*b(2) — b(1)*a(2)
vrts(i, j)%sn = vrts(i, j)%sn / sqrt(sum(vrts(i, j)%sn * vrts(i, j)%sn)) ! Нормализация
end do
a = vrts(i, 1)%p(:) — vrts(i, n)%p
b = vrts(i + 1, 1)%p(:) — vrts(i, n)%p
vrts(i, n)%sn(1) = a(2)*b(3) — b(2)*a(3) ! Координаты вектора внешней нормали к боковой грани
vrts(i, n)%sn(2) = a(3)*b(1) — b(3)*a(1)
vrts(i, n)%sn(3) = a(1)*b(2) — b(1)*a(2)
vrts(i, n)%sn = vrts(i, n)%sn / sqrt(sum(vrts(i, n)%sn * vrts(i, n)%sn)) ! Нормализация
end do
do j = 1, n ! Нормали в верхнем сечении
vrts(ch, j)%sn = vrts(ch — 1, j)%sn
end do
a = vrts(ch, 2)%p — vrts(ch, 1)%p
b = vrts(ch, n)%p — vrts(ch, 1)%p
top(1) = a(2)*b(3) — b(2)*a(3) ! Координаты вектора внешней нормали к крышке
top(2) = a(3)*b(1) — b(3)*a(1)
top(3) = a(1)*b(2) — b(1)*a(2)
top = top / sqrt(sum(top * top)) ! Нормализация
end subroutine norm
end subroutine parabinit
call fglCullFace(GL_BACK) ! Запрещен вывод граней, смотрящих на нас нелицевой стороной
call fglEnable(GL_CULL_FACE) ! Активизируем режим GL_CULL_FACE
сохранены для снижения объема вычислений.
Получение гладкой закраски параболоида обеспечивает замена
Также меняется порядок назначения нормалей вершин боковых граней: каждая вершина получает «свою» нормаль.
call fglBegin(gl_quads) ! Вывод боковых граней
do i = 1, ch — 1
ii = i + 1
do j = 1, n — 1
jj = j + 1
call fglNormal3f(vrts(i, j)%sn(1), vrts(i, j)%sn(2), vrts(i, j)%sn(3))
call fglVertex3f(vrts(i, j)%p(1), vrts(i, j)%p(2), vrts(i, j)%p(3))
call fglNormal3f(vrts(i, jj)%sn(1), vrts(i, jj)%sn(2), vrts(i, jj)%sn(3))
call fglVertex3f(vrts(i, jj)%p(1), vrts(i, jj)%p(2), vrts(i, jj)%p(3))
call fglNormal3f(vrts(ii, jj)%sn(1), vrts(ii, jj)%sn(2), vrts(ii, jj)%sn(3))
call fglVertex3f(vrts(ii, jj)%p(1), vrts(ii, jj)%p(2), vrts(ii, jj)%p(3))
call fglNormal3f(vrts(ii, j)%sn(1), vrts(ii, j)%sn(2), vrts(ii, j)%sn(3))
call fglVertex3f(vrts(ii, j)%p(1), vrts(ii, j)%p(2), vrts(ii, j)%p(3))
end do
j = n; jj = 1
call fglNormal3f(vrts(i, j)%sn(1), vrts(i, j)%sn(2), vrts(i, j)%sn(3))
call fglVertex3f(vrts(i, j)%p(1), vrts(i, j)%p(2), vrts(i, j)%p(3))
call fglNormal3f(vrts(i, jj)%sn(1), vrts(i, jj)%sn(2), vrts(i, jj)%sn(3))
call fglVertex3f(vrts(i, jj)%p(1), vrts(i, jj)%p(2), vrts(i, jj)%p(3))
call fglNormal3f(vrts(ii, jj)%sn(1), vrts(ii, jj)%sn(2), vrts(ii, jj)%sn(3))
call fglVertex3f(vrts(ii, jj)%p(1), vrts(ii, jj)%p(2), vrts(ii, jj)%p(3))
call fglNormal3f(vrts(i, jj)%sn(1), vrts(i, jj)%sn(2), vrts(i, jj)%sn(3))
call fglVertex3f(vrts(ii, j)%p(1), vrts(ii, j)%p(2), vrts(ii, j)%p(3))
end do
call fglEnd ! Заканчиваем вывод боковых граней
Отображение нормалей
Для демонстрации нормалей в конец кода вывода освещенного параболоида следует добавить подпрограмму showNorm и вызов перед переброской данных в буфер кадра
call showNorm(1.5) ! Показываем рассчитанные нормали
bret = SwapBuffers(hDC) ! Переброска данных в буфер кадра
subroutine showNorm(p) ! Отображение нормалей, рассчитанных подпрограммой norm
use paravals
use IFOPNGL
integer(4) :: i
real(4) :: y, p ! p — масштабный коэффициент
real(4) :: v(3) ! Координаты начала (конца) выводимого отрезка (нормали)
call fglDisable(gl_lighting) ! Отключаем расчет освещенности
call fglLineWidth(1.0) ! Задание толщины линии
call fglColor3f(1.0, 0.0, 1.0) ! Задание текущего цвета
call fglBegin(gl_lines)
do i = 1, ch ! Вывод нормалей
y = vrts(i, 1)%p(2)
do j = 1, n
v = (/ vrts(i, j)%p(1), y, vrts(i, j)%p(3) /)
call fglVertex3fv(loc(v))
v = v + p * vrts(i, j)%sn(:)
call fglVertex3fv(loc(v))
end do
end do
call fglEnd
call fglLineWidth(3.0)
call fglColor3f(1.0, 0.0, 0.0) ! Текущий цвет красный
call fglBegin(gl_lines)
v = (/ 0.0, vrts(ch, 1)%p(2), 0.0 /) ! Нормаль к крышке
call fglVertex3fv(loc(v))
v = v + 4.0 * top
call fglVertex3fv(loc(v))
call fglEnd
call fglFlush
end subroutine showNorm
Результат показан на рис. 19.
Рис. 19. Параболоид и его нормали
Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Заключение
В случае невыпуклых фигур при выводе граней нужно применять тест глубины (используется метод z-буфера):
call fglEnable(GL_DEPTH_TEST) ! Активизируем тест глубины
call fglDepthFunc(GL_LESS) ! Значение GL_LESS действует по умолчанию
Тест глубины оперирует нормализованными координатами вершин. По умолчанию буфер глубины инициализирован значением 1.0. Эту величину можно изменить, например задав:
call fglClearDepth(0.7) ! Глубина — параметр из диапазона [0.0, 1.0]
! Инициализация буфера цвета и буфера глубины
call fglClear(ior(gl_color_buffer_bit, GL_DEPTH_BUFFER_BIT))
Протяженность буфера глубины устанавливается командой
call fglDepthRange(near, far) ! near, far — значения из диапазона [0.0, 1.0]
Текущее значение инициализации буфера глубины вернет подпрограмма fglGetFloatv, вызванная с параметром GL_DEPTH_CLEAR_VALUE, например:
real(4) z(1)
call fglGetFloatv(GL_DEPTH_CLEAR_VALUE, z) ! Массив z содержит значение инициализации буфера глубины
Протяженность буфера глубины возвращается той же подпрограммой, вызванной с параметром GL_DEPTH_RANGE, например:
real(4) rng(2)
call fglGetFloatv(GL_DEPTH_RANGE, rng) ! Массив rng содержит протяженность буфера глубины
Полученные данные можно поместить для последующего просмотра, например, в файл a.txt:
open(2, file = ‘a.txt’)
write(2, *) z
write(2, *) rng
Буфер глубины можно защитить от записи, применив команду
call fglDepthMask(flag) ! Запись в буфер глубины производится, если flag отличен от нуля
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Приложение 1. Файл GLUtilsMod.f90 с функцией CreateOpenGLWindow
! GLUtilsMod.f90
module GLUtilsMod
use IFWINA
use, intrinsic :: ISO_C_BINDING
implicit none
private
public :: CreateOpenGLWindow, hInstance, hPalette
integer(HANDLE) :: hInstance = NULL
integer(HANDLE) :: hPalette = NULL
contains
function CreateOpenGLWindow(title, x, y, width, height, pixelType, flags, WindowProc) result(hWnd)
implicit none
integer(HANDLE) :: hWnd ! Результат функции
! Заголовок окна вывода
character(*), intent(IN) :: title
! Начальные позиция и размер окна
integer(SINT), intent(IN) :: x, y, width, height
! Pixel Format Descriptor для iPixelType
integer(BYTE), intent(IN) :: pixelType
! Pixel Format Descriptor для dwFlags
integer(DWORD), intent(IN) :: flags
interface
integer(LONG) function WindowProc (hWnd, uMsg, wParam, lParam)
!DEC$ ATTRIBUTES STDCALL :: WindowProc
import
integer(HANDLE) :: hWnd
integer(UINT) :: uMsg
integer(fWPARAM) :: wParam
integer(fLPARAM) :: lParam
end function WindowProc
end interface
type, bind(C) :: OUR_LOGPALETTE
integer(WORD) palVersion
integer(WORD) palNumEntries
type(T_PALETTEENTRY) palPalEntry(0:255)
end type OUR_LOGPALETTE
type(T_WNDCLASSEX) :: wc
type(OUR_LOGPALETTE) :: lPal
type(T_LOGPALETTE), pointer :: lPal2
type(T_PIXELFORMATDESCRIPTOR) :: pfd
integer(HANDLE) :: hDC, hRet
character(LEN(title) + 1) :: lcl_title
integer(DWORD) :: ret
integer(SINT) :: n, pf, i, redmask, greenmask, bluemask
integer(USHORT) :: class_atom
character(*), parameter :: szClassName = «OpenGL»C
if (hInstance == NULL) then
hInstance = GetModuleHandle(NULL)
wc%cbSize = sizeof(wc)
wc%style = CS_OWNDC
wc%lpfnWndProc = loc(WindowProc)
wc%cbClsExtra = 0
wc%cbWndExtra = 0
wc.hInstance = hInstance
wc.hIcon = LoadIcon(0_HANDLE, int(IDI_WINLOGO,LPVOID))
wc.hCursor = LoadCursor(0_HANDLE, int(IDC_ARROW,LPVOID))
wc.hbrBackground = (COLOR_WINDOW + 1) !NULL
wc.lpszMenuName = NULL
wc.lpszClassName = loc(szClassName)
wc.hIconSm = NULL
class_atom = RegisterClassEx(wc)
if (class_atom == 0) then
ret = MessageBox(NULL, «RegisterClass: не могу зарегистрировать класс окна.»C, «Ошибка»C, MB_OK)
hWnd = NULL
return
end if
end if
! Создаем окно
lcl_title = trim(title) // CHAR(0)
hWnd = CreateWindowEx(0,szClassName, &
lcl_title, &
IOR(WS_OVERLAPPEDWINDOW,IOR(WS_CLIPSIBLINGS,WS_CLIPCHILDREN)), &
x, y, width, height, NULL, NULL, hInstance, NULL)
if (hWnd == NULL) then
ret = GetLastError()
ret = MessageBox(NULL, «CreateWindow: Не могу создать окно.»C, «Ошибка»C, MB_OK);
return
end if
hDC = GetDC(hWnd)
! Обнуляем все поля Pixel Format Descriptor
call ZeroMemory (loc(pfd), sizeof(pfd))
pfd%nSize = sizeof(pfd)
pfd%nVersion = 1
pfd%dwFlags = ior(PFD_DRAW_TO_WINDOW, PFD_SUPPORT_OPENGL)
pfd%dwFlags = ior(pfd%dwFlags, flags)
pfd%iPixelType = pixelType
pfd%cColorBits = 32
pf = ChoosePixelFormat (hDC, pfd)
if (pf == 0) then
ret = MessageBox(NULL, «ChosePixelFormat: Не могу подыскать подходящий формат пикселей.»C, «Ошибка»C, MB_OK)
hWnd = 0
return
end if
ret = SetPixelFormat (hDC, pf, pfd)
if (ret == 0) then
ret = MessageBox(NULL, «SetPixelFormat: Не могу установить заданный формат пикселей.»C, «Ошибка»C, MB_OK)
hWnd = 0
return
end if
ret = DescribePixelFormat (hDC, pf, int(sizeof(pfd),UINT), pfd)
! Настройка палитры
if ((iand(pfd%dwFlags, PFD_NEED_PALETTE) /= 0) .or. (pfd%iPixelType == PFD_TYPE_COLORINDEX)) then
n = ishft(1, pfd%cColorBits)
if (n > 256) n = 256
call ZeroMemory (loc(lPal), sizeof(lPal))
lPal%palVersion = Z’300′
lPal%palNumEntries = n
ret = GetSystemPaletteEntries(hDC, 0, n, lPal%palPalEntry(0))
if (pfd%iPixelType == PFD_TYPE_RGBA) then
redmask = ishft(1,pfd%cRedBits) — 1
greenmask = ishft(1,pfd%cGreenBits) — 1
bluemask = ishft(1,pfd%cBlueBits) — 1
do i = 0, n — 1
lPal%palPalEntry(i)%peRed = (iand(ishft(1,pfd%cRedShift),redmask) * 255) / redmask
lPal%palPalEntry(i)%peGreen = (iand(ishft(1,pfd%cGreenShift),greenmask) * 255) / greenmask
lPal%palPalEntry(i)%peBlue = (iand(ishft(1,pfd%cBlueShift),bluemask) * 255) / bluemask
end do
else
lPal%palPalEntry(0)%peRed = 0;
lPal%palPalEntry(0)%peGreen = 0;
lPal%palPalEntry(0)%peBlue = 0;
lPal%palPalEntry(0)%peFlags = PC_NOCOLLAPSE;
lPal%palPalEntry(1)%peRed = 255;
lPal%palPalEntry(1)%peGreen = 0;
lPal%palPalEntry(1)%peBlue = 0;
lPal%palPalEntry(1)%peFlags = PC_NOCOLLAPSE;
lPal%palPalEntry(2)%peRed = 0;
lPal%palPalEntry(2)%peGreen = 255;
lPal%palPalEntry(2)%peBlue = 0;
lPal%palPalEntry(2)%peFlags = PC_NOCOLLAPSE;
lPal%palPalEntry(3)%peRed = 0;
lPal%palPalEntry(3)%peGreen = 0;
lPal%palPalEntry(3)%peBlue = 255;
lPal%palPalEntry(3)%peFlags = PC_NOCOLLAPSE;
end if
call c_f_pointer(c_loc(lPal), lPal2)
hPalette = CreatePalette(lPal2)
if (hPalette /= NULL) then
hret = SelectPalette(hDC, hPalette, FALSE) ! Имя в GDI32
ret = RealizePalette(hDC)
end if
end if
ret = ReleaseDC(hDC, hWnd)
return
end function CreateOpenGLWindow
end module GLUtilsMod
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Приложение 2. Файл GLWinMain.f90 с функцией WinMain
! GLWinMain.f90
function WinMain(hCurrentInst, hPreviousInst, lpszCmdLine, nCmdShow)
!DEC$ ATTRIBUTES STDCALL,DECORATE,ALIAS:»WinMain» :: WinMain
use IFWINA ! Это альтернативная версия ifwin, в которой переименованы процедуры, конфликтующие с QuickWin
use IFOPNGL
use GLUtilsMod ! См. прил. 1
use glMod
implicit none
integer(SINT) :: WinMain
integer(HANDLE), intent(IN) :: hCurrentInst, hPreviousInst
integer(LPCSTR), intent(IN) :: lpszCmdLine
integer(SINT), intent(IN) :: nCmdShow
! Локальные переменные
integer(HANDLE) :: hRC ! Контекст OpenGL
integer(HANDLE) :: hWnd ! Окно
type(T_MSG) :: msg ! Сообщение
integer(DWORD) :: buffer = PFD_DOUBLEBUFFER ! Двойная буферизация
integer(BYTE) :: color = PFD_TYPE_RGBA ! Система цветов RGBA
integer(SINT) :: ret
integer(HANDLE) :: hret
integer(BOOL) :: bret
WinMain = 0
hWnd = CreateOpenGLWindow(«GL faces», 0, 0, 256, 256, color, buffer, WindowProc)
if (hwnd == NULL) return
hDC = GetDC(hWnd) ! Получаем контекст OpenGL
hRC = fwglCreateContext(hDC)
hret = fwglMakeCurrent(hDC, hRC)
bret = ShowWindow(hWND, SW_SHOW)
bret = UpdateWindow(hWnd)
! Цикл обработки сообщений
do while (GetMessage(msg, NULL, 0, 0))
if (msg%message == WM_QUIT) exit
bret = TranslateMessage(msg)
bret = DispatchMessage(msg)
call display
end do
hret = fwglMakeCurrent(NULL,NULL)
ret = ReleaseDC(hDC, hWnd)
hret = fwglDeleteContext(hRC)
bret = DestroyWindow(hWnd)
if (hPalette /= NULL) bret = DeleteObject(hPalette)
return
end function WinMain
Видео:Уравнение плоскости через 3 точкиСкачать

Приложение 3. Функции WindowProc файла GLMod.f90
integer(LONG) function WindowProc(hWnd, uMsg, wParam, lParam)
!DEC$ ATTRIBUTES STDCALL :: WindowProc
integer(HANDLE) :: hWnd ! Обработчик окна
integer(UINT) :: uMsg ! Сообщение
integer(fWPARAM) :: wParam ! Параметр сообщения
integer(fLPARAM) :: lParam ! Параметр сообщения
type(T_PAINTSTRUCT) :: ps
integer(HANDLE) :: hret
integer(BOOL) :: bret
WindowProc = FALSE
select case (uMsg) ! Описание типов сообщений см. в MSDN
case (WM_PAINT)
call display
hret = BeginPaint(hWnd, ps)
hret = EndPaint(hWnd, ps)
return
case (WM_SIZE)
call fglViewport (0, 0, int(ibits(lParam,0,16),UINT), int(ibits(lParam,16,16),UINT))
bret = PostMessage(hWnd, WM_PAINT, 0, 0)
return
case (WM_CHAR)
select case (wParam)
case (ichar(‘q’)) ! Нажимаем q для выхода
call PostQuitMessage(0)
case (ichar(‘r’)) ! Вводим пробел для поворота прямоугольников
rtt = .true. ! Используется только при выводе сторон грани
end select
return
return
case (WM_PALETTECHANGED)
if (hWnd == ZEXT(wParam, HANDLE)) then
bret = UnrealizeObject(hPalette) ! hPalette из GLUtilsMod
bret = SelectPalette(hDC, hPalette, FALSE)
bret = RealizePalette(hDC)
WindowProc = TRUE
return
end if
return
case (WM_QUERYNEWPALETTE)
if (hPalette /= NULL) then
bret = UnrealizeObject(hPalette) ! hPalette из GLUtilsMod
bret = SelectPalette(hDC, hPalette, FALSE)
bret = RealizePalette(hDC)
WindowProc = TRUE
return
end if
return
case (WM_CLOSE)
call PostQuitMessage(0)
return
end select
WindowProc = DefWindowProc(hWnd, uMsg, wParam, lParam)
end function WindowProc
Видео:Видеоурок "Нормальное уравнение прямой"Скачать

Приложение 4. Вкладка Solution окна проекта Visual Studio
Рассматриваемые примеры создавались в среде Microsoft Visual Studio как windows-приложения.
Рис. 20. Вкладка Solution в окне проекта Visual Studio
Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

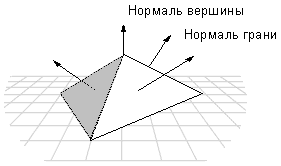
Вектор нормали к грани
Каждая грань объекта имеет перпендикулярный вектор нормали. Вектор определяет направление вершин, в котором они находится (в левосторонней или правосторонней системе координат). В Direct3D Вы видите только передние грани (лица). На таких гранях вершины распределяются по часовой стрелке.
Любая грань, которая является не передним, является задним (или обратным). Direct3D всегда не отображает задние грани. Вы, если захотите, можете изменить способ отображения, чтобы обратная сторона появилась. Для более полной информации смотрите Режим выбора.
Приложение Direct3D не должна определять нормаль грани; система их вычисляет автоматически, когда это необходимо. Система использует нормаль грани для режима плоской закраски (для плоских объектов). В режиме закраски Гуро (Gourand), Direct3D использует нормали вершин. Также нормали вершин можно использовать для создания эффектов над текстурами и освещения.
Когда Вы применяете закраску Гуро (Gourand) к многоугольнику, Direct3D использует нормали вершин, чтобы вычислить угол между источником освещения и поверхностью многоугольника. Это рассчитывает цвет и значение интенсивности для вершины и интерполирует их для каждой точки поверхности всего примитива. Direct3D вычисляет значение интенсивности используя угол. Чем больше угол, тем меньше отражается свет от поверхности.
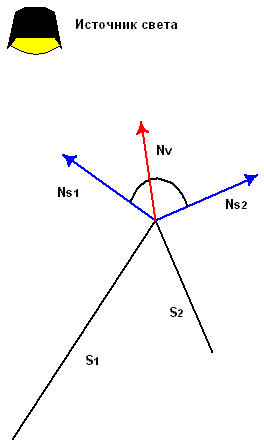
Если Вы создали объект, стороны которого являются плоскими, то нормали вершин будут направлены перпендикулярно поверхности, как показано ниже на рисунке:
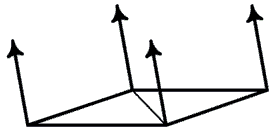
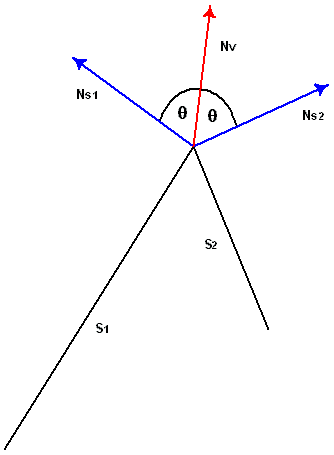
У Вас может быть ситуация, когда объект составлен сверху из нескольких треугольников и треульники не копланарные. Единственный простой способ добиться плавной закраски всех треугольников, это сначала вычислить вектор нормали поверхности для каждого лица многоугольника с которым вершина связана. И установить вектор нормали так, чтобы угол был равный между всеми векторами нормали поверхности. Но этот метод недостаточно эффективен для некоторых примитивов. Ниже, на рисунке, показана некая фигура у которой есть две поверхности S1 и S2, соединяющиеся в верхней части. Вектор нормали поверхностей S1 и S2 отображается синим цветом. Нормаль самой вершины показан красным цветом. Угол между нормалью поверхности S1 и нормалью вершины одинаковый с углом между нормалью поверхности S2 и этой же нормали вершины. Когда эти две поверхности будут освещены и закрашены методом Гуро (Gourand), получите результат гладкого (закругленного) края между поверхностями.
Если вектор нормали отклонился к одному из лиц, к которым он связан, это увеличит или уменьшит отражаемый свет к той или иной поверхности, в зависимости от угла к источнику. Посмотрите на нижний рисунок:
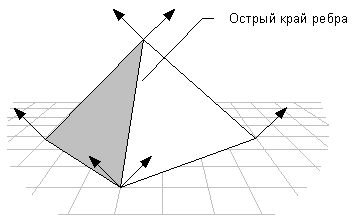
Вы можете воспользоваться закраской Гуро (Gouraud), чтобы показать некоторые объекты в трехмерной сцене с острыми гранями.
Чтобы это сделать, дублируйте вектор нормали вершины на любом пересечении грани (лица), где требуется острый край, как это показано ниже на рисунке:
Если Вы используете функцию DrawPrimitive для отображения сцены, определите объект с острыми гранями в списке треугольников. Когда Вы инициализируете объект из множества треугольников, Direct3D обратится к ним, как объект состоящий их большого количества треугольников. Закраску Гуро (Gourand) можно применить не только к граням многоугольника, но и к смежным граням. В результате Вы получите объект с гладкой поверхностью от грани к грани. Поскольку список треугольников — это многоугольник, состоящий из нескольких непересекающихся треугольных граней, Direct3D применяет закраску Гуро (Gouraud) к каждой грани многоугольника. Но если имеются в списке (массиве) два и более смежных треугольника, то они будут иметь острый край между собой.
Поэтому нужно применить другую плоскую закраску, перед тем как объект отобразится с острыми ребрами. Этот способ наиболее эффективный, но он может создать объекты в сцене не так реалистично, как к объектам применяя закраска Гуро (Gouraud).
🎥 Видео
5. Нормальное уравнение плоскости выводСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Репетитор по математике ищет нормаль к плоскостиСкачать

Координаты вектора. 9 класс.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать