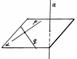
Связь между параллельными прямыми и прямыми перпендикулярными к плоскости (3 видео)

§ 8. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости

Мы постоянно видим, что перпендикуляры к одной и той же плоскости параллельны. Например, вертикальные отрезки параллельны между собой. Эти отрезки могут представляться параллельно стоящими столбами или мачтами, стволами стройных сосен в корабельном лесу, колоннами зданий музея (рис. 84) или вертикальными опорами моста и т. д.

Эта изящная геометрия выражается в теореме, которую мы сейчас докажем.

8.1 Параллельность прямых, перпендикулярных одной плоскости

Теорема 8 (о параллельности перпендикуляров). Две прямые, перпендикулярные одной и той же плоскости, параллельны.

Доказательство. Пусть две прямые а и b перпендикулярны плоскости а и пересекают её соответственно в точках А и В (рис. 85). Проведём через прямую а и точку В плоскость р и покажем, что прямая b также лежит в плоскости β.

В плоскости а возьмём отрезок MN, перпендикулярный отрезку АВ и имеющий точку А своей серединой. Так как AM = AN и АВ ⊥ MN, то ВМ = BN.

Возьмём на прямой b любую точку С ≠ В и проведём отрезки СA, CM, CN. Поскольку b ⊥ a, то треугольники СВМ и CBN прямоугольные. Они равны, так как имеют общий катет СВ и равные катеты ВМ и BN. Поэтому CM = CN, т. е. треугольник CMN равнобедренный. Его медиана СА является также его высотой, т. е. СA ⊥ MN.

Итак, три прямые, проходящие через точку А, — АС, АВ и а — перпендикулярны прямой MN. По теореме о плоскости перпендикуляров (п. 7.2) они лежат в одной плоскости — плоскости β, которая проходит через прямые АВ и а.

Поскольку прямая АС лежит в плоскости β, то точка С ∈ β. Значит, прямая b лежит в плоскости β (как и прямая а). Но в плоскости β прямые а и b перпендикулярны одной и той же прямой АВ (так как a ⊥ α, то b ⊥ α и прямая АВ лежит в α). Поэтому b||а.

Доказанная теорема является признаком параллельности прямых в пространстве.

8.2 Параллель к перпендикуляру

В этом пункте мы докажем теорему, обратную теореме о параллельности перпендикуляров.

Теорема 9 (о параллели к перпендикуляру). Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.

Доказательство. Пусть две прямые а и b параллельны и а перпендикулярна плоскости а (рис. 86). Прямая b пересекает плоскость α в некоторой точке В (по лемме пункта 3.3). Имеются две возможности:

b ⊥ α;
b не перпендикулярна α.

Предположим, что выполняется вторая. Тогда проведём через точку В прямую с ⊥ α (задача п. 7.3). По теореме о параллельности перпендикуляров с||α. Получилось, что через точку В проходят две прямые, параллельные прямой а, что невозможно.

Теорема о параллели к перпендикуляру является ещё одним признаком перпендикулярности прямой и плоскости.

Содержание

Связь между параллельностью прямых и их перпендикулярностью к плоскости.
Теоремы,устанавливающие связь между параллельностью
Геометрия 10 класс
🎬 Видео

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Связь между параллельностью прямых и их перпендикулярностью к плоскости.

1.Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

2.Если две прямые перпендикулярны к плоскости, то они параллельны.

Связь между параллельными прямыми и прямыми перпендикулярными к плоскости

Признак перпендикулярности прямой и плоскости. Теорема. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.

1.Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой, и притом единственная.

2.Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

3.Если две плоскости перпендикулярны к прямой, то они параллельны.

Прямая а, пересекающая плоскость , называетсяперпендикулярной к плоскости, если она перпендикулярна к любой прямой в плоскости , проходящей через точку пересечения прямой а с плоскостью .

Видео:10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Теоремы,устанавливающие связь между параллельностью

Скачать
презентациюТеорема о двух параллельных прямых >>

Теоремы,устанавливающие связь между параллельностью прямых и их перпендикулярностью к плоскости. Теорема 2:Если две прямые перпендикулярны к плоскости,то они параллельны между собой. Терема 1:Если одна из двух параллельных прямых перпендикулярна к плоскости,то и другая прямая перпендикулярна к этой плоскости.

Слайд 8 из презентации «Условие перпендикулярности прямой и плоскости». Размер архива с презентацией 415 КБ.

Видео:ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ перпендикулярные к плоскости 10 классСкачать

Геометрия 10 класс

«Примеры симметрии в природе» — Симметрия в геологии. Симметрия цилиндра. Симметрия в биологии. Виды симметрии. Симметрия в географии. Примеры симметричного распределения. Симметрия в природе. Что такое симметрия. Дискретная симметрия. Человек, многие животные и растения обладают двусторонней симметрией. Природные объекты. Симметрия является фундаментальным свойством природы. Симметрия внешней формы кристалла. Симметрия в физике.

«Задачи на построение сечений» — Тетраэдр. Середины ребер. Точки. Точка. Построение сечений. Сечение параллелепипеда. Уровень. Меню. Сечение параллелепипеда плоскостью. Площадь сечения. Постройте сечение тетраэдра. Найдите точку пересечения прямой. Сечение куба. Куб. Сечение тетраэдра. Данные точки. Многогранник. Искомое сечение. Середины. Постройте сечение куба плоскостью.

«Следствия из аксиом стереометрии» — Постройте изображение куба. Диктант. Самостоятельная работа. Сформулируйте теорему. Найдите прямую пересечения плоскостей. Аксиомы стереометрии и их простейшие следствия. Слайды по геометрии. Ответ объясните. Различные плоскости. Сколько граней проходит через одну,две,три,четыре точки. Существование плоскости. Пересечение прямой с плоскостью. Назовите линию пересечения этих плоскостей. Прямые,пересекающиеся в точке.

«Симметрия в окружающем мире» — Большинство простых молекул обладает элементами пространственной симметрии. Геометрия в цветах. Пифагор. Симметрия в математике. Цветок жизни. Радиальная симметрия. Платоновые тела. Симметрия в живой природе. Древние греки. Симметрия в химии. Сакральная геометрия. Актиноморфная симметрия. Биообъекты с совершенной точечной симметрией. Переносы. Симметрия вокруг нас. Симметрия.

«Основные аксиомы стереометрии» — Древняя китайская пословица. Геометрические тела. Предмет стереометрии. Геометрия. Четыре равносторонних треугольника. Следствия из аксиом. Пирамида Хеопса. Точки прямой лежат в плоскости. Основные фигуры в пространстве. Плоскость. Первые уроки стереометрии. Следствия из аксиом стереометрии. Аксиома. Плоскости имеют общую точку. Источники и ссылки. Изображения пространственных фигур. Аксиомы стереометрии.

«Параллелепипед» — В параллелепипед можно вписать тетраэдр. Вывод формулы объёма прямоугольного параллелепипеда. Отрезок, соединяющий две вершины. У параллелепипеда противолежащие грани параллельны и равны. Произвольный параллелепипед. Так параллелепипед выглядит в развертке. Площадь поверхности прямоугольного параллелепипеда. Прямоугольный параллелепипед. «Зальцбургский параллелепипед». Параллелепипед симметричен относительно середины его диагонали.

Всего в теме «Геометрия 10 класс» 54 презентации