Логико математический анализ понятия треугольник

Просмотр содержимого документа
«Методика обучения учащихся математическим понятиям.»

Выполнить логико-математический анализ понятия: обыкновенная дробь,

неправильная дробь, отрицательное число, биссектриса угла, медиана треугольника, квадратичная функция, окружность:

— выявить вид определения;

— определить структуру определения (каким союзом связаны признаки понятия: и (конъюктивно), или (дизъюктивно));

— раскрыть математическое содержание каждого элемента определения (термин, род, видовые отличия).

— определить объем и содержание понятия.

Определение понятия «обыкновенная дробь»:

Обыкновенные дроби – это записи вида 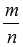(или m/n), где m и n – любые натуральные числа. Структура конъюктивная: признаки соединены союзом «и». Ближайший род— дробь. Видовые отличия: 1) числитель равен знаменателю, 2) числитель меньше знаменателя, 3) числитель больше знаменателя. Вид определения: определение вербально явное через род и видовые отличия. Объем и содержание понятия: Обыкновенные дроби используют для описания числа долей. Числитель располагается над дробной чертой, а знаменатель-под дробной чертой.
Числителем обыкновенной дроби m/n называется натуральное число m, которое показывает количество взятых равных долей из единого целого. Знаменателем обыкновенной дроби m/n называется натуральное число n, которое показывает, на сколько равных долей разделено единое целое. Обыкновенная дробь дает возможность записывать результат деления двух натуральных чисел, для которых не выполняется деление нацело. Все дробные числа, которые отвечают обыкновенным дробям, можно отобразить на координатном луче. При сравнении двух обыкновенных дробей, если выясняется, что они не равны, можно узнать, какая из них больше, а какая — меньше другой. Для этого используют правило сравнения обыкновенных дробей: нужно привести дроби к общему знаменателю и затем сравнить их числители. У какой дроби числитель будет больше, та дробь и будет являться большей.

Определение понятия «неправильная дробь»:

Неправильная дробь— дробь у которой числитель равен или больше знаменателя. Структура дизъюктивная: признаки соединены союзом «или». Ближайший род-дробь. Видовые отличия: числитель равен знаменателю, числитель больше знаменателя. Объем и содержание понятия: Неправильные дроби используют для описания числа долей. Числитель располагается над дробной чертой, а знаменатель-под дробной чертой.
Числителем неправильной дроби m/n называется натуральное число m, которое показывает количество взятых равных долей из единого целого. Знаменателем неправильной дроби m/n называется натуральное число n, которое показывает, на сколько равных долей разделено единое целое. Неправильная дробь дает возможность записывать результат деления двух натуральных чисел, для которых не выполняется деление нацело.

Определение понятия: «Отрицательное число»:

Отрицательное число-это элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Ближайший род: натуральное число. Видовые отличия: числа меньше 0, числа со знаком минус. Объем и содержание понятия: любое отрицательное число меньше любого положительного, из двух отрицательных чисел меньше то, что распологается левее на координатной оси, ноль больше любого отрицательного числа. Структура конъюктивная: признаки соеденены союзом «и».

Определение понятия «Биссектриса угла»:

Биссектриса угла: луч с началом в вершине угла, делящий угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла. Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. Ближайший род:прямая. Видовые отличия: Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. Объем и содержание понятия: Точки биссектрисы угла треугольника равноудалены от сторон этого угла. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности. Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне. Есть еще понятие «биссектриса угла», которая является лучом и точно так же делит угол (любой, не обязательно треугольника) пополам. Структура конъюктивная: признаки соеденены союзом «и».

Определение понятия «Медиана треугольника»

Медиана – это отрезок, соединяющий высоту и середину противоположной стороны. В треугольнике три вершины, а значит и медианы три. Медианы не всегда совпадают с высотами или биссектрисами. Чаще всего это отдельные отрезки. Ближайший род: прямая. Видовые отличия: Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.

Все медианы треугольника пересекаются в одной точке. Структура конъюктивная: признаки соеденены союзом «и». Объем и содержание понятия: Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника). Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1, считая от вершины треугольника. Точку пересечения медиан треугольника называют центроидом треугольника. Медианы треугольника делят треугольник на 6 равновеликих треугольников.

Определение понятия «Квадратичная функция»

Функция вида y=ax^2+bx+c, где a не равно 0, b и c ­– любые числа (они и называются коэффициентами). Число a называют старшим или первым коэффициентом такой функции, b – вторым коэффициентом, а c – свободным членом называется квадратичной функцией. Ближайший род: функции. Структура конъюктивная: признаки соединены союзом «и». Видовые отличия: Графиком квадратичной функции y = x2 является квадратичная парабола. Объем и содержание понятия: Ось y является осью симметрии параболы y = x2 или что парабола симметрична относительно оси y. Ось симметрии как бы разрезает параболу на две части, которые обычно называют ветвями параболы. У параболы есть особая точка, в которой смыкаются обе ветви и которая лежит на оси симметрии параболы — точка (0;0). Данная точка называется вершиной параболы. Свойства функции y = x21) y = 0 при x = 0; y 0 при x 0 и при x 0, то ветви направлены вверх ;если a

Определение понятия «Окружность»

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Ближайший род: замкнутая плоская кривая. Структура конъюктивная: признаки соединены союзом «и». Видовые отличия: Окружностью называют линию, которая ограничивает круг. . Объем и содержание понятия: Окружность имеет центр — это начальная точка нарисования циркулем. Если задуманная точка лежит на окружности, это означает, что она ей принадлежит. Можно обозначить дуги окружности, ими будут любые 2 точки, ограничивающие окружность, т. е. любые две точки A и B окружности разбивают ее на две части; каждая из этих частей и называется дугой. Если провести линию через эти точки, то получим хорду. А хорда, проходящая через центр окружности, имеет название диаметра. Если же от центра провести линии к точке на окружности, то получится радиус окружности.

2. Разработать методику введения данного понятия конкретно-индуктивным методом.

1. Обыкновенная дробь (5 класс).

2. Отрицательные числа (6 класс).

Результат выполнения задания 2 представить в виде таблицы:

Предметные результаты: правильно употреблять в речи определение “обыкновенная дробь” и «отрицательные числа», знать свойства, уметь записывать обыкновенные дроби и отрицательные числа, уметь строить координатную ось и определять на ней положительные, отрицательные, дробные числа, отличать дроби друг от друга по признакам, выполнять правильно необходимые вычислительные действия при решении заданий, решать задания с применением знаний по темам: «Обыкновенные дроби» и «Отрицательные числа»

1. Обыкновенная дробь (5 класс). Цель: ввести определение понятия «обыкновенная дробь» путем конкретного примера.

Метод: частично- поисковый.

Организовывает урок. Отбирает материал для урока. Готовит наглядный материал на тему –«обыкновенные дроби». Ставит познавательные задачи и создает необходимые условия для успешного протекания учения.

(Запишите задачу в тетрадь. Ребята давайте проанализируем все три решенные задачи. Что мы в них находили? Приходим к выводу что нам необходимо число, которое охарактеризует одну или несколько равных частей.

Обьяснение понятия долей.

Выводим существенные признаки:

Содержит одну или несколько равных частей (долей)

Визуализация записи дроби

Число под чертой показывает (знаменует) на сколько равных частей разделили, поэтому под чертой начали называть знаменатель.

Число над чертой показывает сколько таких равных частей взяли. В старину говорили сколько числится , поэтому начали называть числителем. Для закрепления раздает карточки и вместе с учениками подводит итоги.

Слушают задание. Анализируют. Работают самостоятельно и с учителем у доски. Наблюдавю за демонстрациями учителя. Обьясняют наблюдаемое. Отвечают на вопросы и задают вопросы.

Решают задачу: 1)Ребята купили шоколадку разделили ее на 10 равных частей. Саша съел 3 части, а Коля 5 частей. Какую часть шоколадки съел Саша, а какую Коля?

1.На сколько равных частей разделили шоколадку?

2.Сколько съел Саша?

3.Сколько съел Коля?

Ответ:1. на 10 равных частей

2. 3 части из 10 равных

3. 5 частей из 10 равных

Записывают все в рабочие тетради. Отвечают на вопросы.

Выполнение задания по ограничению понятия и подводят итоги.

2.Отрицательные числа(6 класс) Цель: ввести определение понятия «отрицательное число» путем конкретного примера. Чертеж на доске координатной прямой. Вводит понятие «вправо», «влево». Откладывает точки на оси, максимально визиализирует понятие отрицательного числа. Пользуется такими дополнительными средствами визуализации как термометр уличный.Вводит существенные признаки отрицательных чисел. Разбирает понятие на примере задания. Знакомит учащихся со свойствами отрицательных чисел.

Слушают задание. Рассматривают в учебнике пример. Анализируют. Работают самостоятельно и с учителем у доски. Иллюстрируют и записывают все в тетрадь. Наблюдают за демонстрациями учителя. Обьясняют наблюдаемое. Знакомятся со свойствами, признаками отрицательных чисел путем решения заданий. Отвечают на вопросы учителя. Задают вопросы учителю.

В учебнике отдельно дается определение действия сложения чисел с разными знаками, формулировки этих правил содержат указание на следующие действия. В учебнике большое время уделяется к тому как подойти к действию сложению. Основное внимание уделяется к рассмотрению конкретных задач, обращаясь при этом к координатной прямой. Подводят итоги.

Видео:КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать

Технология работы с понятием «Равнобедренный треугольник»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

«Технология работы с определением понятия «равнобедренный треугольник»

Треугольник называется равнобедренным , если две его стороны равны.

( Геометрия : Учеб. для 7 – 9 кл. ср. шк. /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 3-е изд. – М.: Просвещение, 1992. – 355 с.: ил., страница 34).

Видео:Математический анализ, 15 урок, АссимптотыСкачать

Логико-математический и дидактический анализ формулировки определения понятия «равнобедренный треугольник»

I . Логико-математический анализ.

1. Анализ формулировки.

а) вид определения : через род и видовые отличия;

б) родовое понятие – треугольник

видовые отличия : две стороны равны;

в) содержание понятия : две стороны равны; углы при основании равны; биссектриса, проведённая к основанию, является медианой и высотой; углы при основании острые

объём понятия : множество равнобедренных треугольников

г) таблица истинности

две стороны равны

2. Доказательство существования: построение.

4. Отрицание определения.

Если в треугольнике нет пары равных сторон, то треугольник не является равнобедренным.

5. Связь между новым понятием и изученными ранее.

Равнобедренные треугольники тесно связаны с такими понятиями, как треугольник, сторона треугольника, равные отрезки, равные углы, высота, медиана, биссектриса и т.п.

6. Классификация системы понятия.

II . Дидактический анализ.

7. Для учеников определение не является новым по структуре и формулировке.

8. Система упражнений для актуализации.

1. Сформулируйте определения следующих понятий:

б) вершины треугольника;

г) стороны треугольника;

д) периметр треугольника.

2. Можно ли назвать треугольниками фигуры, изображённые на рисунках? Почему?

3. Начертите произвольный треугольник и назовите его  MKP . Назовите его вершины и стороны.

9. Учитель вовлекает учеников в исследовательскую деятельность и ученики считают себя настоящими исследователями.

1. В геометрии принято классифицировать или, разделять на группы фигуры по каким-либо признакам. Каждая группа изучается отдельно и выявляются свойства, которыми обладают фигуры этой группы. Например, треугольники можно на несколько групп в зависимости от количества равных между собой сторон треугольника. Сколько всего сторон имеет треугольник?

2. Тогда как вы думаете, на сколько групп можно разделить треугольники в зависимости от количества равных между собой сторон? (На три: в треугольнике могут быть все стороны разной длины, т.е. нет равных сторон; две стороны равной длины; все стороны равны между собой.)

3. Сегодня мы выделим группу «равнобедренных треугольников» и будем использовать их при решении задач. Но для того, чтобы использовать какое-либо понятие в практике, нам необходимо дать строгое математическое определение этого понятия.

4. Сформулируйте цель нашего урока.

(Выявить содержание понятия «равнобедренный треугольник» и дать строгое математическое определение этому понятию).

10. Определение вводится с помощью наглядно-конструктивного метода.

11.Упражнения на осознание логической структуры определения.

(треугольник равнобедренный) (две стороны треугольника равны)

12. Упражнения на формирование умения подводить объект под понятие.

1. Какое из следующих предложений является определением равнобедренного треугольника?

а) треугольник, у которого две стороны равны, является равнобедренным;

б) треугольник называется равнобедренным, если две его стороны равны.

2. Найдите все треугольники, изображённые на рисунке. Есть ли среди них те, которые можно назвать равнобедренными? Если да, то какие.

3. Известно, что  АВС =  MKP . Можно ли назвать  АВС равнобедренным, если  MKP равнобедренный?

13. Частные эвристики, позволяющие подводить объект под понятие:

чтобы доказать, что треугольник равнобедренный достаточно найти в нём две равные стороны.

14. Упражнения на овладение действием отыскания следствий на этапе осознания и осмысления.

1. Назовите свойство равнобедренного треугольника, вытекающее из определения равнобедренного треугольника.

2. Известно, что треугольник  АВС равнобедренный с основанием АВ . Назовите свойства, которыми обладает  АВС .

3.  АВЕ – равнобедренный с основанием ВЕ . Найдите:

а) АВ , если АЕ = 5 см;

б) ВЕ , если АВ = 2 ВЕ , а периметр  АВЕ равен 50 см.

15. Частные эвристики, позволяющие выводить следствия из принадлежности объекта понятию:

из того, что треугольник равнобедренный следует, что две его стороны равны;

из того, что треугольник равнобедренный и длина одной из его боковых сторон равна а , следует, что длина другой боковой стороны так же равна а ;

если известно: треугольник равнобедренный, длина одной из боковых сторон (или отношение длины боковой стороны к длине основания) и периметр треугольника, то можно найти длину основания;

если известно: треугольник равнобедренный, длина одной из боковых сторон (или отношение длины боковой стороны к длине основания) и длина основания (или боковой стороны), то можно найти периметр треугольника.

Видео:Математика это не ИсламСкачать

Выводы из логико-дидактического анализа понятия «равнобедренный треугольник»

Тема «Равнобедренные треугольники» является очень важной для учеников:

1. сравнительно простой материал для изучения при небольшом «геометрическом» опыте школьников;

2. на равнобедренных треугольниках школьники учатся исследованию свойств многоугольников, обладающих определёнными качествами, поскольку равнобедренный треугольник – это первый частный случай треугольников (и многоугольников), с которым сталкиваются ученики;

3. доказательства свойств равнобедренного треугольника не являются очень сложными для восприятия, поэтому на них можно обучать различным методам доказательства;

4. при доказательстве свойств равнобедренного треугольника используется первый признак равенства треугольников, пройденный несколько уроков назад. Тема «Признаки равенства треугольников» является сложной для учеников, поэтому её применение не в стандартных задачах, а при исследовании геометрических фигур способствует лучшему её усвоению;

5. после изучения свойств равнобедренного треугольника ученики, пользуясь тем, что любой равносторонний треугольник является также равнобедренным, устанавливают некоторые свойства равносторонних треугольников.

Так как из того, что треугольник является равнобедренным, следует равенство двух его сторон, то можно выделить первый тип задач – на выведение следствий. Известно, что треугольник равнобедренный.

1. Найти длину боковой стороны (или основания), если известен периметр треугольника и соотношение длины одной из боковых сторон к длине основания.

2. Найти периметр треугольника, если известна длина боковой стороны (или основания) и соотношение длины боковой стороны к длине основания.

Второй тип задач – на подведение объекта под понятие равнобедренного треугольника, т.е. нужно установить, является ли треугольник равнобедренным. Например:

1. Установить, какие из треугольников, изображённых на рисунке, равнобедренные?

2. Выбрать верное определение из нескольких предложенных высказываний.

3. Даны два равных треугольника и известно, что один из них равнобедренный. Будет ли второй треугольник равнобедренным?

Видео:Логика. Основы Логики. Логическое МышлениеСкачать

Фрагмент урока по введению понятия «равнобедренный треугольник»

Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и трёх отрезков прямых, соединяющих эти точки.

Эти три точки называются вершинами, а отрезки – сторонами треугольника.

Что такое периметр треугольника?

Периметром треугольника называется положительное число, равное сумме длин всех сторон треугольника.

Посмотрите на рисунок и скажите, можно ли назвать треугольниками фигуры, изображённые на нём? Почему?

а) нельзя, т.к. точки А, В, С лежат на одной прямой;

б) нельзя, т.к. точки Р и К соединены кривой, а не отрезком прямой;

в) можно, т.к. точки E , F , G не лежат на одной прямой и каждая пара точек соединена отрезком прямой.

В геометрии принято классифицировать или, разделять на группы фигуры по каким-либо признакам. Каждая группа изучается отдельно и выявляются свойства, которыми обладают фигуры этой группы. Например, треугольники можно на несколько групп в зависимости от количества равных между собой сторон треугольника. Сколько всего сторон имеет треугольник?

Тогда как вы думаете, на сколько групп можно разделить треугольники в зависимости от количества равных между собой сторон?

На три: в треугольнике могут быть все стороны разной длины, т.е. нет равных сторон; две стороны равной длины; все стороны равны между собой.

Сегодня мы выделим группу «равнобедренных треугольников» и будем использовать их при решении задач.

постановка учебной задачи и планирование решения УЗ

Но для того, чтобы использовать какое-либо понятие в практике, нам необходимо дать строгое математическое определение этого понятия. Сформулируйте цель нашего урока.

Выявить содержание понятия «равнобедренный треугольник» и дать строгое математическое определение этому понятию.

II. Операционно-познавательный этап

доказательство существования и выявление существенных свойств

Постройте произвольный отрезок и назовите его АВ .

Постройте прямую, проходящую через точку В , но не проходящую через точку А . Назовите прямую а .

С помощью циркуля на прямой а от точки В отложите отрезок, равный АВ . Назовите его ВС .

Отметьте на рисунке равенство отрезков АВ и ВС .

Соедините точки А и С .

Какую получили фигуру?

Чем являются для треугольника АВС отрезки АВ , ВС и АС ?

Сравните стороны АВ и ВС .

Итак, мы получили треугольник, обладающий некоторым свойством. Каким?

Две стороны АВ и ВС равны.

В этом случае  АВС называют равнобедренным. Сформулируйте чётко определение равнобедренного треугольника.

Треугольник называется равнобедренным, если две его стороны равны.

При этом равные стороны треугольника называют боковыми сторонами, а третью сторону – основанием.

Тогда стороны АВ и ВС – это …

боковые стороны  АВС .

осознание логической структуры определения

Построим новый равнобедренный треугольник АВС и выпишем то, что мы только что получили.

На доске и в тетрадях появляются записи:

 АВС – равнобедренный:

АВ, ВС – боковые стороны

(треугольник равнобедренный) (две стороны треугольника равны)

Говорят, что  АВС – равнобедренный с основанием АС .

подведение под понятие

Какое из следующих предложений является определением равнобедренного треугольника? Почему?

а) треугольник, у которого две стороны равны, является равнобедренным;

б) треугольник называется равнобедренным, если две его стороны равны.

б). В обоих утверждениях сказано о равенстве двух сторон, но в предложении а) есть слово «является», чего не может быть в определении.

Как с помощью определения установить, что треугольник равнобедренный?

Нужно найти в этом треугольнике две равные стороны.

Для того, чтобы установить, что треугольник равнобедренный достаточно найти в нём пару равных сторон.

Далее учитель вешает плакат:

Найдите все треугольники, изображённые на рисунке. Если да, то какие.

Есть ли среди них те, которые можно назвать равнобедренными? Если да, то назовите их, указав основание и боковые стороны.

 EOF : EF – основание, EO и OF – боковые стороны.

 EFL : LF – основание, EL и EF – боковые стороны.

 MKN : все стороны являются основаниями и боковыми сторонами. Всё зависит от конкретного выбора пары равных сторон.

Известно, что  АВС =  MKP . Можно ли назвать  MKP равнобедренным, если  MKP  АВС равнобедренный?

Можно. МК = (треугольники равны) = АВ = (  АВС равнобедр.) = ВС = (треуг. равны) = КР, т.е. МК = КР . Тогда  MKP равнобедренный по определению равнобедренного треугольника..

Назовите свойство равнобедренного треугольника, вытекающее из определения равнобедренного треугольника.

Две стороны равны

Известно, что треугольник  АВС равнобедренный с основанием АВ . Назовите свойства, которыми обладает  АВС .

АС = ВС – боковые стороны.

Постройте  АВЕ – равнобедренный с основанием ВЕ .

Решим задачу. Найдите:

а) АВ , если АЕ = 5 см;

б) ВЕ , если АВ = 2 ВЕ , а периметр  АВЕ равен 50 см.

Запишем, что дано и что следует найти для задачи а) и воспользуйтесь определением равнобедренного треугольника.

а)Дано:  АВЕ – равнобедр., ВЕ — основание, АЕ = 5 см.

 АВЕ – равнобедр., тогда по определению равнобедр. треуг. АВ = АЕ = 5 см (по усл.), т.е АВ = 5 см .

Теперь решим задачу б)

б)Дано:  АВЕ – равнобедр., ВЕ — основание, АВ = 2 ВЕ,

Воспользуйтесь определением равнобедренного треугольника.

 АВЕ – равнобедр., тогда по определению равнобедр. треуг. АВ = АЕ .

Выразите боковые стороны через основание.

АВ = 2 ВЕ (по усл)

Выразите периметр треугольника через его основание.

Тогда 5 ВЕ = 50 см

Ответ: ВЕ = 10 см .

Итак, какова же была цель нашего урока?

Выявить содержание понятия «равнобедренный треугольник» и дать строгое математическое определение этому понятию.

Достигли ли мы её?

Сформулируйте определение равнобедренного треугольника.

Треугольник называется равнобедренным, если две его стороны равны.

Какие специальные названия имеют стороны равнобедренного треугольника?

Равные стороны равнобедренного треугольника называются боковыми сторонами, а третья – основанием.

Сегодня мы дали строгое определение равнобедренным треугольникам. Но настоящие исследователи обычно не останавливаются на этом и продолжают исследования и открывают новые факты. Какое у вас возникает предположение?

Нужно продолжить исследование равнобедренных треугольников.

Чем, по-вашему, мы будем заниматься на следующем уроке?

Будем пытаться открыть новые факты, касающиеся равнобедренных треугольников.

Видео:Математический анализ, 6 урок, ПроизводнаяСкачать

Портал педагога

Автор: Кустарева Марина Ивановна
Должность: учитель математики
Учебное заведение: МОУ-СОШ №13
Населённый пункт: город Клин Московская область
Наименование материала: методическая разработка
Тема: «Логико- дидактический анализ понятия равнобедренного треугольника»
Раздел: среднее образование

Логико- дидактический анализ понятия равнобедренного треугольника

Учебник «Геометрия, 7-9 классы», автор Л.С. Атанасян и др.

§2. Медианы, биссектрисы и высоты треугольника.

п.18. Свойства равнобедренного треугольника.

Определение. Треугольник называется равнобедренным, если две его стороны равны.

а) вид определения: через род и видовые отличия

б) родовое понятие: треугольник

видовые отличия: две стороны равны

в)содержание понятия: две стороны равны; углы при основании равны; углы при

основании острые; биссектриса, проведённая к основанию ,является медианой и

объем понятия: множество равнобедренных треугольников

Доказательство существования: построение.

Если в треугольнике нет пары равных сторон, то треугольник не является

Связь между новым понятием и изученными ранее.

Равнобедренные треугольники тесно связаны с такими понятиями, как треугольник,

сторона треугольника, равные отрезки, равные углы, высота, медиана, биссектриса и т.п.

. Доказательство существования: построение.

Для учеников определение не является новым по структуре и формулировке.

Подведение под понятие.

1. Сформулируйте определения следующих понятий:

б) вершины треугольника;

г) стороны треугольника;

д) периметр треугольника.

2. Можно ли назвать треугольниками фигуры, изображённые на рисунках? Почему?

3. Начертите произвольный треугольник и назовите его

MKP. Назовите его вершины и

Учитель вовлекает учеников в исследовательскую деятельность и ученики считают себя

1. В геометрии принято классифицировать или, разделять на группы фигуры по каким-

либо признакам. Каждая группа изучается отдельно и выявляются свойства, которыми

обладают фигуры этой группы. Например, треугольники можно на несколько групп в

зависимости от количества равных между собой сторон треугольника. Сколько всего

сторон имеет треугольник?

2. Тогда как вы думаете, на сколько групп можно разделить треугольники в зависимости

от количества равных между собой сторон? (На три: в треугольнике могут быть все

стороны разной длины, т.е. нет равных сторон; две стороны равной длины; все стороны

равны между собой.)

3. Сегодня мы выделим группу «равнобедренных треугольников» и будем использовать

их при решении задач. Но для того, чтобы использовать какое-либо понятие в практике,

нам необходимо дать строгое математическое определение этого понятия.

4. Сформулируйте цель нашего урока.

(Выявить содержание понятия «равнобедренный треугольник» и дать строгое

математическое определение этому понятию).

Определение вводится с помощью наглядно-конструктивного метода.

Упражнения на осознание логической структуры определения.

∆АВС равнобедренный: АВ = ВС.

(две стороны треугольника равны)

Упражнения на формирование умения подводить объект под понятие.

1. Какое из следующих предложений является определением равнобедренного

а) треугольник, у которого две стороны равны, является равнобедренным;

б) треугольник называется равнобедренным, если две его стороны равны.

2. Найдите все треугольники, изображённые на рисунке. Есть ли среди них те, которые

можно назвать равнобедренными? Если да, то какие.

MKP. Можно ли назвать

13. Частные эвристики, позволяющие подводить объект под понятие:

чтобы доказать, что треугольник равнобедренный достаточно найти в нём две равные

Классификационная схема понятия

Схема определения понятия равнобедренного треугольника:

две стороны равны

Логико- дидактический анализ теоремы об углах при основании

Учебник «Геометрия, 7-9 классы», автор Л.С. Атанасян и др.

§2. Медианы, биссектрисы и высоты треугольника.

п.18. Свойства равнобедренного треугольника.

Свойство1. В равнобедренном треугольнике углы при основании равны.

а) Вид формулировки теоремы: категоричный;

условие: треугольник равнобедренный

заключение: углы при основании равны

простая теорема (одно условие и одно заключение).

Логический смысл теоремы: свойство.

б) Метод доказательства – аналитико-синтетический;

при доказательстве используется приём дополнительного построения (этот приём

является новым для учеников);

в основе доказательства лежит первый признак равенства треугольников, определение

биссектрисы угла и то, что в равных треугольниках против соответственно равных сторон

лежат равные углы.

Пошаговая запись доказательства теоремы

Т е о р е м а : в равнобедренном треугольнике углы при основании равны.

🎦 Видео

Введение в логику, урок 1: Базовые понятияСкачать

Суть матанализа, Глава 1Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.Скачать

Математический анализ, 1 урок, Предел числовой последовательностиСкачать

Переставь одну цифру! Задача на логикуСкачать

Математический анализ. Алексей Савватеев и Александр Тонис. Лекция 1.1. Как далеко видно с горыСкачать

✓ Введение в математический анализ. Множество действительных чисел | матан #001 | Борис ТрушинСкачать

Математический Анализ. Лекция 1. Введение.Тема 1. Символы и понятия.Скачать

Введение в математический анализ 1. Множества и функцииСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Отюцкий Г.П. принимает логикуСкачать