Выберите хорду окружности возможно несколько вариантов ответов kl

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

ДАЮ 160 БАЛЛОВ. ПОМОГИТЕ СРОЧНО 1. Выбери хорду окружности (возможно несколько вариантов ответов): ON KL MN NR OK 2. Справедливы ли данные суждения? 1. Если прямая — касательная окружности, то она имеет только одну общую точку с окружностью. Да Нет 2. Если прямая и окружность имеет одну общую точку, то прямая является касательной к окружности. Нет Да 3. Если прямая проходит через центр окружности, то она пересекает окружность в двух точках. Да Нет 3. Которое из утверждений неверно? Радиус окружности, вписанной в равносторонний треугольник, можно вычислить: r=h:3 Центр окружности, описанной около равнобедренного треугольника, находится на большей стороне треугольника Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров 4. Дано: ∢ OAC = 45°. Вычисли: ∢ OBA = °; ∢ AOC = °. 5. ∪AB=107°∪AC=92° Найти: угол BOC и угол BAC. Ответ: угол BOC= °, угол BAC= °. 6. Дано: MN=KL=5,5см;∢MNO=60°. Найти: диаметр см; ∢MNR= °; ∢NKL= °. 7. В треугольнике ABC серединный перпендикуляр стороны BC пересекает сторону AC в точке D. Определи длины отрезков AD и DC, если BD = 9 см и AC = 12 см. AD = см; DC = см. 8. Вычисли неизвестную сторону четырёхугольника, если в него вписана окружность. neregulars cetrsturis ar burtiem.JPG FG= 4 см; EH= 9 см; FE = 6 см; HG = см. 9. В треугольник вписана окружность. Вычисли неизвестные углы, если ∢ NMO = 33° и ∢ ONL = 38°. 12ok.png ∢ AOC = °; ∢ BOA = °; ∢ BOC = °.

1) Если прямая касательная окружности, то она имеет две общие точки с окружностью.

2) Если прямая и окружность имеют общую точку, то прямая является касательной окружности.

3) Прямая и окружность могут иметь только две общие точки.

1) Выбери хорду окружности (возможно несколько вариантов ответов): ON KL MN NR OK

2) Справедливы-ли данные суждения?

-Да(Ну, нечем объяснить. Уж простите)

3) Которое из утверждений неверно? Радиус окружности, вписанной в равносторонний треугольник, можно вычислить: r=h:3 Центр окружности, описанной около равнобедренного треугольника, находится на большей стороне треугольника Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.

-Потому как 1 и 3 верно.

4. Дано: ∢ OAC = 45°. Вычисли: ∢ OBA = °; ∢ AOC = °

-Центр вписанной в угол окружности лежит на биссектрисе угла

углы: OAC = OAB = 45°

радиусы в точку касания перпендикулярны касательной.

углы: ABO = АСО = 90°

сумма острых углов прямоугольного треугольника = 90°

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Тест по теме «Окружность»

Тест состоит из 10 заданий. Включает в себя теоретические вопросы с выбором ответа и ключевые задачи по теме. К тесту даны ответы.

Просмотр содержимого документа
«Тест по теме «Окружность»»

Тест по теме «Окружность»

Множество точек плоскости равноудалённых от некоторой точки.

Отрезок, соединяющий точку окружности с центром

Отрезок, соединяющий любые две точки окружности и проходящий через центр

Выберите правильный или правильные ответы

А) радиус в два раза больше диаметра

Б) хорда может быть в окружности только одна

В) диаметр в два раза больше радиуса

Выберите правильную запись соотношения радиуса и диаметра

А 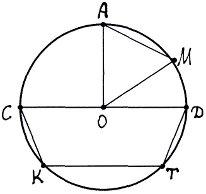) R=D:2

Б) R=D 2

хорды: радиусы: диаметры:

Найдите диаметр окружности, если ОМ=7,4

Диаметр окружности равен 20 см, найдите КТ, если известно, что КТ в 1,2 раза больше радиуса

Окружности с диаметрами 30 дм и 40 дм касаются друг друга. Найдите расстояние между их центрами

Радиус одной окружности 140 см, другой 90 см, расстояние между и центрами равно 50 см. Определите взаимное расположение окружностей.

Тест по теме «Окружность»

Множество точек плоскости равноудалённых от некоторой точки, как называется эта точка

Хорда, проходящая через центр

Отрезок, соединяющий любые две точки окружности

Выберите правильный или правильные ответы

А) радиус в два раза меньше диаметра

Б) хорд может быть в окружности бесконечно много

В) диаметр в два раза меньше радиуса

Выберите правильную запись соотношения радиуса и диаметра

А ) R=D:2

Б) R=D 2

Выпишите: хорды: радиусы: диаметры:

Найдите радиус окружности, если СД=15

Диаметр окружности равен 48 см, найдите АМ, если известно, что АМ в 1,2 раза меньше радиуса

Окружности с диаметрами 10 дм и 50 дм касаются друг друга. Найдите расстояние между их центрами

Радиус одной окружности 6 см, другой 7 см, расстояние между и центрами равно 12 см. Определите взаимное расположение окружностей.

Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Решебник по математике «Тренировочный вариант 3 ОГЭ по математике по демоверсии 2021 года с решением»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:5 вариант ЕГЭ Ященко 2024 математика профильный уровень 🔴Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

№ 1 Условие задания: 1 Б.

Установи соответствие между форматами листов и их размерами:

Самый большой размер у формата В0, ширина этого формата является длиной формата В1, ширина которого в свою очередь является длиной формата В2 и т.д. Значит, чем больше номер формата, тем меньше его размеры :

В России сегодня используется стандарт бумажного листа ISO 216. Всего в этом

стандарте есть три серии — A, B, C. Наиболее известный в России формат серии A, который используется для документов и чертежей. О существовании серии B мало кто знает, она используется в полиграфии для печати, например, книг и открыток. Серия C используется, например, для изготовления конвертов к форматам серии A. Все три стандарта основываются на делении листа на части, отчего все форматы стандарта оказываются подобными фигурами. Это предназначено для удобного масштабирования от формата к формату без потери полей и пропорций.

Рис. 1. Серия ISO 216 A

Представлена таблица, в которой даны размеры четырѐх листов в миллиметрах — B1, B3, B5, B7. Установи соответствие между форматами листов и их размерами:

№ 2 Условие задания: 1 Б.

Определи, сколько листов формата B5 можно сделать из листа формата B3.

РЕШЕНИЕ: Из листа формата В3 получается два листа формата В4, а из листа формата В4 получается два листа

формата В5. Т.о, из формата В3 получается 4 листа формата

№ 3 Условие задания: 1 Б.

найди площадь листа формата B2 и вырази еѐ в квадратных сантиметрах. В поле для ответа запиши только число, без единиц измерения, ответ округли до сотых.

РЕШЕНИЕ: Лист формата В2 имеет длину, как ширина листа В1, а ширина его равна длине листа формата В3. Т.о. еѐ размеры 707×500 . S = 707 500=353500 _мм 2 ;

353500:100=3535 _см 2 . ОТВЕТ: 3535

№ 4 Условие задания: 1 Б.

В России сегодня используется стандарт бумажного листа ISO 216. Всего в этом стандарте есть три серии — A, B, C. Наиболее известный в России — формат серии A, который используется для документов и чертежей. О существовании серии B мало кто знает, она используется в полиграфии для печати, например, книг и открыток. Серия C используется, например, для изготовления конвертов к форматам серии A. Все три стандарта основываются на делении листа на части, отчего все форматы стандарта оказываются подобными фигурами. Это предназначено для удобного масштабирования от формата к формату без потери полей и пропорций.

Номер Размер, мм, длина × ширина

В таблице даны размеры четырѐх листов в

Рис. 1. миллиметрах, первое число — длина, второе

— ширина. Установи, пользуясь таблицей, ширину листа бумаги

Ответ: 300 формата A3 и округли ответ до ближайшего целого, кратного 10. В поле для ответа запиши только число, без единиц измерения.

Чтобы найти ширину листа заданного формата, нужно сначала установить, в какой строке расположены его размеры.

Номер Размер, мм, длина × ширина Формат

Видим, что лист формата A3 имеет размер 420×297. Первое число — длина, второе — ширина. Значит, нужное нам число — 297 мм. Теперь надо выполнить второе условие, округлить до ближайшего целого, кратного 10. Это значит, что число должно оканчиваться на 0 единиц. Ближайшее — может быть и слева, и справа. Используем правило округления до десятков. 297≈300.

Правильный ответ: 300.

№ 5 Условие задания: 1 Б.

Для каждого вида упаковки бумаги определим цену за 1000 листов: для этого цену за упаковку нужно умножить на столько, сколько раз указанное количество листов входит в тысячу.

Цена за 1000 листов первого вида равна: 162 (1000:250)=648 руб.

Цена за 1000 листов второго вида равна: 157 (1000:200)=785 руб.

Цена за 1000 листов третьего вида равна: 183 (1000:250)=732 руб.

Цена за 1000 листов четвѐртого вида равна: 216 (1000:100)=2160 руб.

Сравнивая значения, получим, что наибольшая цена за 1000 листов: 2160 рублей.

Правильный ответ: 2160 руб.

В магазине продаѐтся бумага в различных упаковках и по различной цене. В

таблице показано количество листов в каждой упаковке и еѐ цена. В какой упаковке бумага стоит дороже?

Какова наибольшая стоимость 1000 листов? (Впиши только значение без единицы измерения.)

№ 6 Условие задания: 1 Б.

РЕШЕНИЕ: При решении данного задания будем пользоваться следующими свойствами степеней:

+ переместительное и сочетательное свойства умножения:

137  29  10   3973  10  3973  1  3973

Правильный ответ: 3973

Найди значение выражения: 137   10  9  9   29  10 81  .

№ 7 Условие задания: 1 Б.

РЕШЕНИЕ: Представим дроби 2/25 и 2/13 в виде десятичных с округлением до трѐх знаков после запятой.

Сравнивая, получим, что между данными числами лежит 0,09. Это 3 вариант.

Правильный ответ: 3.

Какое из следующих чисел заключено между числами и ? В ответе укажи

номер правильного варианта. 1) 0,16; 2) 0,25; 3) 0,09; 4) 0,07.

№ 8 Условие задания: 1 Б.

РЕШЕНИЕ: Преобразуем выражение. a  

Подставим a=−4, y=52 и найдѐм значение выражения.

a      78 a a  4

Правильный ответ: −78.

Найди значение выражения a  при a = −4 и y = 52. a

№ 9 Условие задания: 1 Б.

РЕШЕНИЕ: Перед нами произведение двух выражений. Оно может быть равно нулю в случае, когда либо первый, либо второй множитель равен нулю. Получим два простейших линейных уравнения и решим их.

Сравним корни. 6 здесь — наибольший.

Правильный ответ: 6

еши уравнение и в ответе запиши его наибольший корень.

№ 10 Условие задания: 1 Б.

Частота попаданий первого спортсмена:  0,74

Частота попаданий второго спортсмена:  0,42 . 50

Частота попаданий третьего спортсмена:  0,44.

Частота попаданий четвѐртого спортсмена:  0,62

50 Сравнивая частоту попаданий, получим, что наибольшая —

Правильный ответ: 0,74

В таблице представлены результаты тренировки спортсменов.

На соревнования поедет тот, кто показывает лучшие результаты. Какова частота

удачных выступлений у спортсмена, который поедет на соревнования?

№ 11 Условие задания: 1 Б.

Поскольку гипербола, изображѐнная на рисунке, расположена в 1 и 3 четвертях, то из всех вариантов подходят вариант 1 и вариант 4. Поскольку график данной функции проходит через точку с координатами (1; 4), то ответом будет вариант 1.

y  x

4  ; 4  4

Для остальных функций координаты не обращают формулу в верное равенство

Правильный ответ: 1.

Установи соответствие графика функции, который изображѐн в прямоугольной

системе координат, и формулы. Запиши номер варианта.

1) y  ; x

2) y   ;

3) y   ;

4) y  .

№ 15 Условие задания: 1 Б.

Сумма углов треугольника 180°. Внешний угол треугольника BCD равен сумме двух других углов, не смежных с ним

∠ BCD= ∠ A+ ∠ B=11°.

Правильный ответ: 11.

Дан треугольник ABC, в котором известно, что ∠ A+ ∠ B=11°. Найди внешний

угол этого треугольника, расположенный при вершине C, ответ дай в градусах.

№ 16 Условие задания: 1 Б.

Для того чтобы решить эту задачу, удобно для наглядности соединить все точки отрезками. Тогда легко будет вспомнить, что треугольник AOC равнобедренный, поскольку его сторонами являются радиусы, угол ADC вписанный, а угол AOC — центральный, и он в 2 раза больше угла ADC.

∠ ADC=0,5 ∠ AOC=0,5 ⋅ 82=41°.

Правильный ответ: 41.

Три точки лежат на окружности с центром O. Найди ∠ ADC, если ∠ AOC=82°.

Ответ дай в градусах.

Рис. 1. Окружность и точки

№ 17 Условие задания: 1 Б.

РЕШЕНИЕ: Для нахождения площади квадрата можно воспользоваться формулой нахождения площади ромба.

Так как диагонали квадрата равны, то получим следующую d 2

формулу: S 

Подставим значение диагонали и найдѐм площадь.

S    3960,5.

Правильный ответ: 3960,5.

Диагональ квадрата равна 89. Чему равна площадь квадрата?

№ 18 Условие задания: 1 Б.

РЕШЕНИЕ: Сначала подсчитаем количество клеток, которые занимает наша фигура. На данном рисунке это 8 клеток.

Площадь одной клетки нужно найти, для чего нужно размер стороны возвести в квадрат. S  a 2  0,3 2  0,09 Теперь можно найти площадь всей фигуры, умножив количество клеток на площадь одной.

8 0,09=0,72 .

Правильный ответ: 0,72.

На разлинованной в клетку бумаге изображена фигура.

Рис. 1. Фигура Сторона клетки — 0,3.

Найди площадь этой фигуры и запиши в ответе число без единиц измерения.

№ 19 Условие задания: 1 Б.

1. Окружность является совокупностью точек,

равноудалѐнных друг от друга. Неверно. 2. Градусной мерой дуги окружности является градусная мера центрального угла, опирающегося на эту дугу. Верно.

3. Любой вписанный в окружность треугольник, две вершины которого принадлежат диаметру, прямоугольный. Верно.

4. Треугольники, сторонами которых являются отрезки

пересекающихся хорд, подобны. Верно. Истинность высказываний устанавливается при помощи соответствующего раздела учебника по геометрии. Здесь рассматривается часть, посвящѐнная треугольникам и четырѐхугольникам.

Правильный ответ: 1

Выбери номер(-а) высказываний, которые неверны. Запиши в порядке

возрастания, если их несколько, без пробелов, запятых и других дополнительных символов.

1. Окружность является свокупностью точек, равноудалѐнных друг от друга. 2. Градусной мерой дуги окружности является градусная мера центрального угла, опирающегося на эту дугу.

3. Любой вписанный в окружность треугольник, две вершины которого принадлежат диаметру, прямоугольный.

4. Треугольники, сторонами которых являются отрезки пересекающихся хорд, подобны.

№ 20 Условие задания: 2 Б.

3. Рассмотрим уравнение k 2  2k  48  0 ,дискриминант которого D = b 2  4a c    2  2  4  1  48 = 4 − 192= −188 отрицателен, значит, уравнение не имеет корней.

5. Рассмотрим уравнение k 2  2k  48  0 .. По теореме Виета

Правильный ответ: −8; 6.

1. Для решения данного уравнения будем использовать формулу разности квадратов: a 2  b 2  =(a−b) (a+b) — и теорему Виета: «Сумма корней приведѐнного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену».

2. Если использовать формулу разности квадратов, уравнение примет вид: (k 2  2k  48)  k 2  2k  48   0 _. .

№ 21 Условие задания: 2 Б.

Здесь нужно рассматривать объѐм запланированной работы и производительность – скорость выполнения работы. Поскольку никаких численных указаний на него нет, возьмѐм его как единицу, 1. Рассмотрим ситуацию и обозначим производительность буквами v с соответствующим номеру индексом.

Очевидно, что в первом случае, для того чтобы получить выполненную работу, нужно умножить на 11 скорость работы каждого и сложить всѐ это.

Во втором описанном случае видно, что каждую скорость нужно умножить на указанное количество часов, и мы получим ту же единицу.

Описывая третий случай при помощи уравнения, мы можем заключить, что для получения единицы нужно взять скорость работы второго за x и точно так же сложить произведения времени на скорость для всех трѐх. Мы получим систему из трѐх уравнений.

Причѐм если сложить первые два, в которых известно время работы для всех трѐх, мы получим двойной объѐм работы. Значит, результат этого сложения нужно разделить пополам:

Таким образом мы получим уравнение, равное по значению третьему. Можно их уравнять и решить получившееся уравнение.

Правильный ответ: 13,5 ч.

Три экскаватора с навесным ковшом роют яму под систему водоотведения.

Трактора имеют разные годы выпуска и разных водителей, поэтому их производительности различаются. Они смогут выполнить работу, если будут трудиться вместе 11 ч подряд. Кроме того, для выполнения этого же объѐма работы можно разделить еѐ по времени так: первый будет работать 9 ч, второй 16 и третий — 8 ч. Сколько времени нужно проработать второму, если до него уже успели потрудиться первый (9,5 ч) и третий (10 ч)? Ответ дай в часах.

№ 23 Условие задания: 2 Б.

Если посмотреть на формулу, на первый взгляд может показаться, что графиком функции будет парабола — по причине наличия переменной во второй степени. Однако имеется ещѐ и переменная в знаменателе алгебраической дроби. Проведѐм тождественные преобразования. Кроме того, будет выколотая точка. Установим еѐ координату на оси абсцисс, приравняв знаменатель к нулю. Затем подставим в преобразованное выражение и получим координату по оси ординат.

y  4 _  1 ; x  0; x  1; y  4 _ x  1 ;y  4 _ 1

Теперь понятно, что графиком этой функции будет гипербола. A(1;3).

Построить схематично график этой функции можно при помощи параллельного переноса и поворота, применѐнного к базовому графику. Асимптотами гиперболы будут оси координатной плоскости, поскольку и значения, и область определения еѐ бесконечно стремятся к нулю, но никогда его не достигают. Минус перед дробью отразит график симметрично оси ординат. Свободный коэффициент 4 сдвинет график на 4 вверх. (Рисунок 1) 1 Здесь пунктиром показана базовая гипербола y  , x

оранжевая гипербола — результат отражения относительно оси ординат. Базовая гипербола никогда не пересечѐт горизонтальную линию, совпадающую с осью абсцисс. Значит, y=4.

Правильный ответ: (Рис. 1) и ответ y=4.

Найди значения параметра, при которых прямая y=b не имеет общих точек с

графиком функции . y  4  x₂  _ 1x . x

РИС.1

№ 23 Условие задания: 2 Б.

Дано: ABCD трапеция; AB=CD; P_ABCD  140 ; BC=20; AD=52.

Решение: Для решения данной задачи будем использовать формулу площади трапеции: S   b  h.

P=AB+CD+BC+AD=2 ⋅ AB+BC+AD (поскольку периметр — это сумма длин всех сторон, и трапеция равнобедренная). Подставим в данное выражение значения периметра и сторон: 140=72+2 ⋅ AB, AB= 34.

Так как трапеция равнобедренная, _то AH _  BC _ 52  20 _ 16.

Найдѐм BH. По теореме Пифагора имеем:

BH  AB 2  AH 2  34 2  16 2  30 .

Так как узнали все компоненты, то найдѐм площадь:

S   b  h  20  52  30  1080 . a

Правильный ответ: 1080.

Известно, что периметр равнобедренной трапеции с

основаниями 20 и 52 равен 140. Определи площадь данной трапеции.

№ 24 Условие задания: 2 Б.

Дан четырѐхугольник PMNO, который можно вписать в окружность.

Если четырѐхугольник можно вписать в окружность, значит, суммы его противоположных углов равны по 180°.Значит ∠ M=180− ∠ PON. ∠ PON=180− ∠ POR.

∠ A=180−(180− ∠ POR)= ∠ POR. Угол R — общий.

Отсюда треугольники подобны по двум парам равных углов, что и требовалось доказать.

Продолжения его противоположных сторон пересекаются в точке R. Докажи, что треугольники RMN и ROP подобны.

№ 25 Условие задания: 2 Б.

Дано: ΔABC; B=90°; BAL= CAL; AL∩OL=K; ACB=50°. Найти: BCK. Решение

1) Построим прямоугольный треугольник ABC с прямым углом B, проведѐм биссектрису угла A

( ABC=90°; BAL= LAC, так как AL — биссектриса).

2) Сделаем дополнительное построение: проведѐм окружность, описанную около треугольника ABC. Тогда получим, что биссектриса пересекает окружность в точке L.

Соединим точки, получим треугольник BCL. Так как BAL= CAL, а AL — биссектриса, то дуга BL равна дуге LC. А раз дуги равны, то хорды, стягивающие эти дуги, также будут равны, отсюда следует, что треугольник BLC — равнобедренный.

3) Проведѐм высоту из вершины L к основанию BC. Так как LN — это высота, опущенная из вершины

равнобедренного треугольника к основанию, то она также является биссектрисой и медианой, тогда BN=BC. Отсюда следует, что LN — серединный перпендикуляр. Это означает, что точка L совпадает с точкой K, то есть с точкой пересечения серединного перпендикуляра к BC и биссектрисой.

4) BCK= BAK (точка L есть точка K) как вписанные углы, опирающиеся на одну и ту же дугу, а BAK=1/2 BAC.

Найдѐм угол BAC:

BAC=90°− ACB (так как сумма острых углов треугольника равна 90°) BAC=90°−50°; BAC=40°.

Значит, угол BCK равен 20°.

Правильный ответ: 20°.

В прямоугольном треугольнике ABC с прямым углом B проведена биссектри-

са угла A. Известно, что она пересекает серединный перпендикуляр, проведѐнный к стороне BC в точке K. Найди угол BCK, если известно, что угол ACB равен 50°.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Тест по теме «Окружность»

Тест состоит из 10 заданий. Включает в себя теоретические вопросы с выбором ответа и ключевые задачи по теме. К тесту даны ответы.

Просмотр содержимого документа
«Тест по теме «Окружность»»

Тест по теме «Окружность»

Множество точек плоскости равноудалённых от некоторой точки.

Отрезок, соединяющий точку окружности с центром

Отрезок, соединяющий любые две точки окружности и проходящий через центр

Выберите правильный или правильные ответы

А) радиус в два раза больше диаметра

Б) хорда может быть в окружности только одна

В) диаметр в два раза больше радиуса

Выберите правильную запись соотношения радиуса и диаметра

А ) R=D:2

Б) R=D 2

хорды: радиусы: диаметры:

Найдите диаметр окружности, если ОМ=7,4

Диаметр окружности равен 20 см, найдите КТ, если известно, что КТ в 1,2 раза больше радиуса

Окружности с диаметрами 30 дм и 40 дм касаются друг друга. Найдите расстояние между их центрами

Радиус одной окружности 140 см, другой 90 см, расстояние между и центрами равно 50 см. Определите взаимное расположение окружностей.

Тест по теме «Окружность»

Множество точек плоскости равноудалённых от некоторой точки, как называется эта точка

Хорда, проходящая через центр

Отрезок, соединяющий любые две точки окружности

Выберите правильный или правильные ответы

А) радиус в два раза меньше диаметра

Б) хорд может быть в окружности бесконечно много

В) диаметр в два раза меньше радиуса

Выберите правильную запись соотношения радиуса и диаметра

А ) R=D:2

Б) R=D 2

Выпишите: хорды: радиусы: диаметры:

Найдите радиус окружности, если СД=15

Диаметр окружности равен 48 см, найдите АМ, если известно, что АМ в 1,2 раза меньше радиуса

Окружности с диаметрами 10 дм и 50 дм касаются друг друга. Найдите расстояние между их центрами

Радиус одной окружности 6 см, другой 7 см, расстояние между и центрами равно 12 см. Определите взаимное расположение окружностей.

Видео:Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)Скачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

📺 Видео

№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать

Демо ОГЭ по математике. Задание 17. Хорда окружности.Скачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Задача на нахождение длины хорды окружностиСкачать

Задачи из ОГЭ. Задания 1-5. Вебинар | МатематикаСкачать

На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Разбор ОГЭ по Математике 2024. Вариант 12 Ященко. Куценко Иван. Онлайн школа EXAMhackСкачать

Разбор ОГЭ по Математике 2024. Вариант 11 Ященко. Куценко Иван. Онлайн школа EXAMhackСкачать

Теорема об отрезках хорд и секущихСкачать