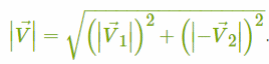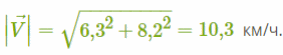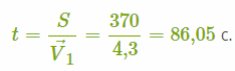В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
- Траектория движения материальной точки через радиус-вектор
- Вектор скорости материальной точки
- Пример нахождения вектора скорости
- Как найти вектор ускорения материальной точки
- Модуль вектора скорости точки
- Модуль вектора ускорения
- Еще примеры решений задачи нахождения вектора скорости и ускорения
- Решение задач на векторы скорости
- А теперь к задачам!
- Решение задач на тему: «Относительность движения и сложение скоростей».
- Просмотр содержимого документа «Решение задач на тему: «Относительность движения и сложение скоростей».»
- 🌟 Видео
Видео:Физика | Ликбез по векторамСкачать

Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Видео:Урок 11. Решение задач на действия с векторамиСкачать

Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Видео:Построение проекции вектора на осьСкачать

Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Видео:Урок 9. Проекции вектора на координатные осиСкачать

Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Видео:Как найти проекцию вектора скорости и ускорения. Выполнялка 112Скачать

Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Решение задач на векторы скорости
Задачи по физике — это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики по кинематике.
Задача на составление описания движения и составление уравнения движения по заданному графику движения
Дано: график движения тела
Найти:
1. составить описание движения
2. составить уравнение движения тела.
Проекцию вектора скорости определяем по графику, выбрав любой удобный для рассмотрения отрезок времени.
Здесь удобно взять t=4c
Составляем уравнение движения тела:
Записываем формулу уравнения прямолинейного равномерного движения.
Подставляем в нее найденный коэффициент Vx (не забываем о минусе!).
Начальная координата тела (Xо) соответствует началу графика, тогда Xо=3
Составляем описание движения тела:
Желательно сделать чертеж, это поможет не ошибиться!
Не забываем, что все физические величины имеют единицы измерения, их необходимо указывать!
Тело движется прямолинейно и равномерно из начальной точки Xо=3м со скоростью 0,75 м/с противоположно направлению оси X.
Задача на определение места и времени встречи двух движущихся тел (при прямолинейном равномерном движении)
Движение тел задано уравнениями движения для каждого тела.
Дано:
1. уравнение движения первого тела
2. уравнение движения второго тела
Найти:
1. координату места встречи
2. момент время (после начала движения), когда произойдет встреча тел
По заданным уравнениям движения строим графики движения для каждого тела в одной системе координат.
Точка пересечения двух графиков движения определяет:
1. на оси t — время встречи ( через сколько времени после начала движения произойдет встреча)
2. на оси X — координату места встречи (относительно начала координат)
В результате:
Два тела встретятся в точке с координатой -1,75 м через 1,25 секунд после начала движения.
Для проверки полученных графическим способом ответов можно решить систему уравнений из двух заданных
уравнений движения:
Для тех, кто почему-то забыл, как построить график прямолинейного равномерного движения:
График движения — это линейная зависимость ( прямая), строится по двум точкам.
Выбираем два любых удобных для простоты расчета значения t1 и t2.
Для этих значений t подсчитываем соответствующие значения координат X1 и X2.
Откладываем 2 точки с координатами (t1, X1) и (t2, X2) и соединяем их прямой — график готов!
Задачи на составление описания движения тела и построение графиков движения по заданному уравнению прямолинейного равномерного движения
Задача 1
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Заданное уравнение сравниваем с формулой и определяем коэффициенты.
Не забываем делать чертеж, чтобы еще раз обратить внимание на направление вектора скорости.
Задача 2
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Задача 3
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Задача 4
Дано: уравнение движения тела
Найти:
1. составить описание движения
2. построить график движения
Тело находится в состоянии покоя в точке с координатой X=4м (состояние покоя — это частный случай движения, когда скорость тела равна нулю).
Задача 5
Дано:
начальная координата движущейся точки xo=-3 м
проекция вектора скорости Vx=-2 м/с
Найти:
1. записать уравнение движения
2. построить график движения
3. показать на чертеже векторы скорости и перемещения
4. найти координату точки через 10 секунд после начала движения
Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Решение задач на тему: «Относительность движения и сложение скоростей».
Примеры и подробное решение задач на тему: «Относительность движения и сложение скоростей».
Перечень разобранных задач:
1. Относительное движение в одном направлении;
2. Относительная скорость тел, движущихся под прямым углом друг к другу;
3. Относительная скорость течения реки;
4. Нахождение времени переплывания реки при движении перпендикулярно течению реки.
Просмотр содержимого документа
«Решение задач на тему: «Относительность движения и сложение скоростей».»
Решение задач на тему:
Относительное движение и сложение скоростей
1. Относительное движение в одном направлении
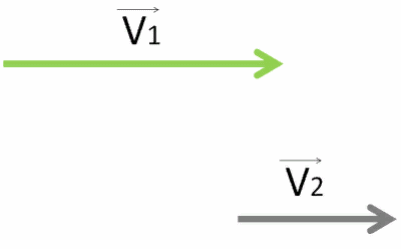
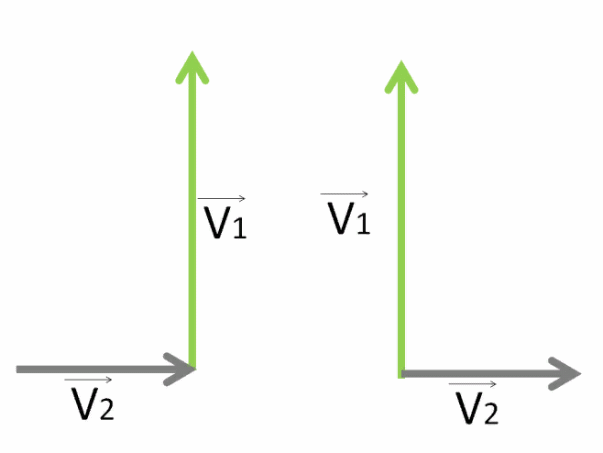
По шоссе движется перевозчик со скоростью 13 м/с. В том же направлении движется другой перевозчик со значением скорости, равным 12,2 м/с. В ответе запиши , с какой скоростью по модулю движется первый перевозчик относительно другого.
Запишем краткое условие к этой задаче.
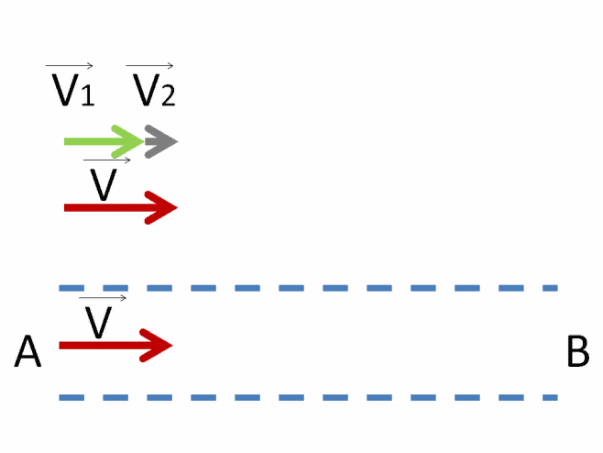
Чтобы найти, с какой скоростью по модулю первый перевозчик движется относительно другого, необходимо заметить, что они оба движутся в одном направлении.
Найти скорость, с которой первый перевозчик движется относительно другого, очень просто.
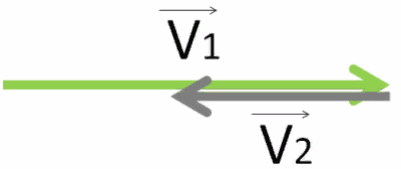
Нужно отнять от его вектора скорости V⃗1 вектор V⃗2 , с которой движется другой перевозчик.
Чтобы это сделать, нужно к вектору V⃗1 прибавить вектор V⃗2, только поменяв его направление.
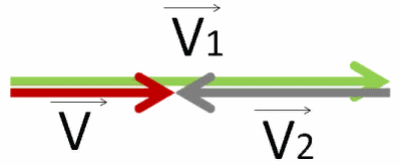
Результирующий вектор V⃗ получим, соединив начало первого вектора с концом последнего.
Получим вектор V⃗ красного цвета.
Чтобы найти его числовое значение, нужно от числового значения вектора V⃗1 отнять числовое значение вектора V⃗2 и результат взять по модулю.
2. Относительная скорость тел, движущихся под прямым углом друг к другу
По свежеположенной дороге перемещается гусеничный трактор , имея скорость 6,3 км/ч. Перпендикулярно движется другой гусеничный трактор со скоростью 8,2 км/ч. Найди значение модуля скорости, с которой движется первый гусеничный трактор относительно другого.
Запишем краткое условие к этой задаче.
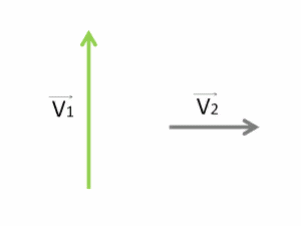
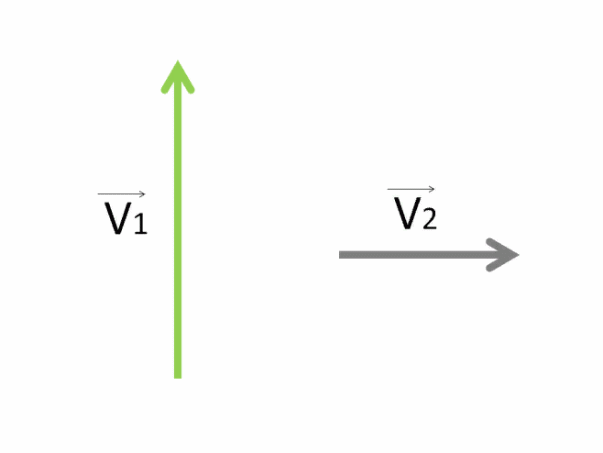
Как мы видим, первый гусеничный трактор движется под углом 90 градусов к другому.
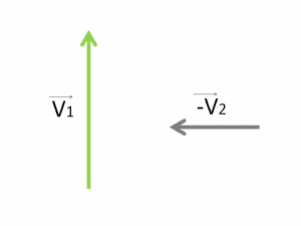
Покажем направления их скоростей с помощью векторов V⃗1 и V⃗2.
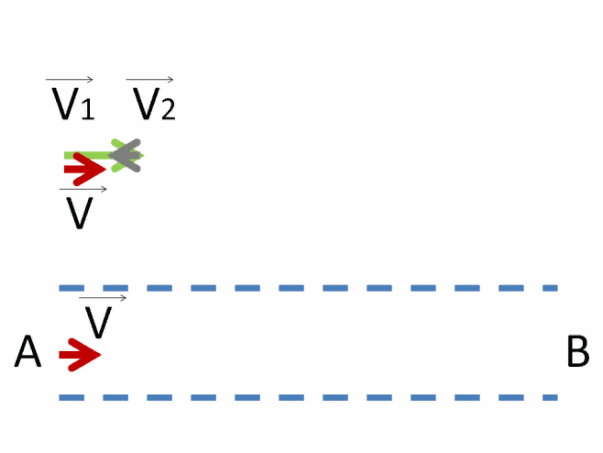
Чтобы найти скорость, с которой движется первый гусеничный трактор относительно другого, необходимо векторно от скорости первого V⃗1 отнять скорость второго V⃗2.
Отнимание вектора V⃗2 проще заменить сложением вектора, противоположного ему: −V⃗2.
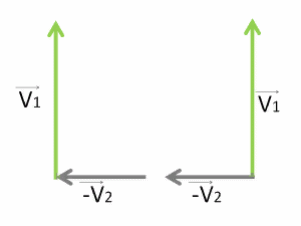
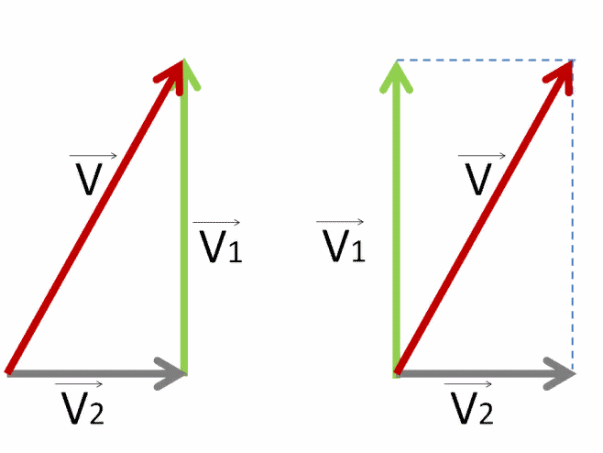
Чтобы найти результирующую скорость V⃗ , необходимо векторно сложить векторы V⃗1 и −V⃗2 . Для интереса попробуем это сделать двумя способами.
Выстраиваем их друг за другом, чтобы получились стороны треугольника.
Или соединяем начала этих векторов — тогда будем использовать правило параллелограмма.
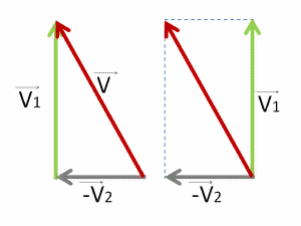
Для сложения по правилу треугольника просто соединяем начало первого вектора с концом последнего.
Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.
Должен получиться один и тот же вектор V⃗ . Изобразим его красным.
Результат сложения не зависит от выбора правила сложения — по правилу треугольника или параллелограмма.
Как видно, у нас получился прямоугольный треугольник со сторонами V⃗1 , −V⃗2 , V⃗ .
По условию задачи нам известны две его стороны, это два катета:
Используя теорему Пифагора, мы можем найти гипотенузу V⃗:
3. Относительная скорость течения реки
Величина скорости пловца вверх по течению реки относительно припаркованного возле магазина мотоцикла — 28,5 км/ч, а вниз по реке — 32,9 км/ч.
Напиши , с какой скоростью по модулю движется река относительно припаркованного возле магазина мотоцикла.
Запишем краткое условие к этой задаче.
Попробуем представить себе, как движется пловец по течению. Если обозначить эту скорость V⃗1, а течение реки V⃗2, то, скорее всего, это будет выглядеть так:
Как видно, результирующий вектор V⃗ получился равным сумме векторов V⃗1 и V⃗2 .
Именно с такой скоростью движется пловец по течению.
Если показывать движение пловца против течения, то с теми же обозначениями получим:
Как видно, уже в этом случае результирующий вектор скорости пловца V⃗ стал меньше, т.к. он равен разности векторов V⃗ 1 и V⃗ 2 . Оно и понятно, ведь против течения двигаться сложнее, скорость пловца меньше из-за встречного течения воды.
Это хорошо, что мы представили себе эту задачу. Но чтобы её решить, нужно составить уравнения движения по течению и против течения реки:
В математике это называется системой уравнений.
Не забывай, что найти нам нужно , с какой скоростью по модулю движется река относительно припаркованного возле магазина мотоцикла, т.е. V⃗2.
Попробуем выразить её из первого уравнения. Для этого V⃗1 перенесётся в правую сторону и поменяет знак:
Как видно, найти значение V2 мы пока не можем, т.к. не знаем скорости пловца V1.
Но для этого нам дано второе уравнение в системе.
Выразим его оттуда.
Нам нужно подставить вместо обозначения V1 его значение 28,5+V2 в уравнение:
В итоге , с какой скоростью по модулю движется река относительно припаркованного возле магазина мотоцикла, мы узнали — 2,2 км/ч.
4. Нахождение времени переплывания реки при движении перпендикулярно к течению реки
Лайнер, двигаясь под углом 90 градусов к течению реки , обладая скоростью 4,3 м/с, переплывает реку шириной 370 м. Скорость течения реки — 2,1 м/с. В ответе укажи время, нужное лайнеру , чтобы переплыть реку.
Запишем краткое условие к этой задаче.
Обозначим скорость лайнера V⃗1, а скорость течения реки V⃗2.
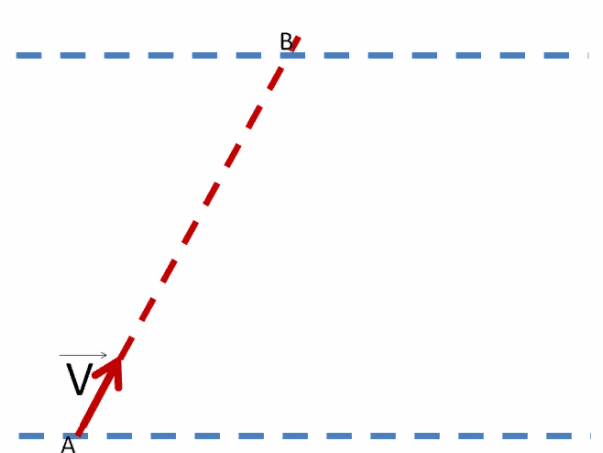
Покажем на рисунке, как направлены векторы их скоростей.
Естественно, лайнер не сможет уже плыть прямо. Течение реки будет действовать вправо и лайнер начнёт смещаться понемногу в ту сторону, куда оно направлено.
Можно показать, конечно, как точно будет направлен результирующий вектор скорости.
Для этого нужно сложить скорости V⃗1 и V⃗2 по правилу треугольника или по правилу параллелограмма.
Правильно это сделать так:
выстраиваем их друг за другом, чтобы получились стороны треугольника
или соединяем начала этих векторов — тогда используем правило параллелограмма.
Для сложения по правилу треугольника просто соединяем начало первого вектора с концом последнего.
Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.
Должен получиться один и тот же вектор V⃗ . Нарисуем его красным цветом.
Лайнер плывёт, но сносится течением реки.
Однако лайнер постоянно стремится переплыть реку со скоростью V⃗1. Именно с этой скоростью лайнер перемещается к противоположному берегу.
Поэтому в данной задаче нам нужна только скорость лайнера V⃗1 и ширина реки 370 м.
Чтобы найти время, нужное лайнеру , чтобы переплыть реку, необходимо всё расстояние в 370 м разделить на скорость лайнера V⃗1.
Итак, время, нужное лайнеру , чтобы переплыть реку, составило 86,05c.
🌟 Видео
Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

ВЕКТОРЫ решение задач 9 класс АтанасянСкачать

Урок 13. Решение задач на РПДСкачать

Мгновенная скорость (видео 6)| Векторы. Прямолинейное движение | ФизикаСкачать

Физика: Понятие Вектор, Вектор СкоростиСкачать

Урок 40. Задачи на движение тела, брошенного под углом к горизонту (ч.1)Скачать

Физика. Векторы. Решение задачСкачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Урок 20. Простейшие задачи на относительность движенияСкачать