Вектор намагниченности на границе двух сред (6 видео)

Условия на границе раздела двух магнетиков

Рассмотрим связь векторов магнитной индукции и напряженности магнитного поля на границе раздела двух магнетиков при отсутствии на границе макротоков. Воспользуемся по аналогии методиками, использованными в задаче о преломлении линий электрического смещения и напряженности электрического ноля на границе раздела двух диэлектриков. Как мы уже видели, на границе магнетика (а в общем случае — на границе раздела двух магнетиков) в поле возникает поверхностный микроток, который может приводить к разрыву нолей.

Рассмотрим сначала соотношение между нормальными к поверхности раздела компонентами вектора магнитной индукции В_п. Воспользуемся теоремой Гаусса, выбрав в качестве гауссовой поверхности поверхность цилиндра (рис. 23.4). При этом основания цилиндра должны быть малы (чтобы считать поле константой), параллельны границе раздела и находиться Рис. 23.4 _в разных магнетиках, а высота цилиндра должна быть

бесконечно малой — в том числе и по сравнению с основаниями. Такой выбор позволяет пренебречь потоком вектора магнитной индукции через боковую поверхность цилиндра но сравнению с потоком через основания.

Тогда из теоремы Гаусса следует, что потоки вектора магнитной индукции через основания по модулю равны, причем один направлен наружу цилиндра, другой внутрь. Геометрически это означает, что потоки направлены в одну сторону: B_niS = B_n2S. Поскольку площади оснований цилиндра Sравны, то получаем, что нормальная компонента вектора магнитной индукции на границе раздела магнетиков остается непрерывной-.

Выразив полученное соотношение через напряженность поля, получим, что нормальная компонента вектора напряженности на границе раздела магнетиков претерпевает разрыв:

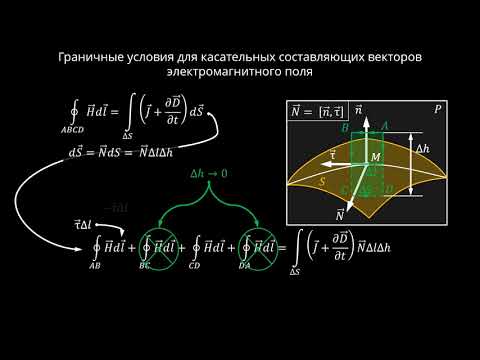
Перейдем теперь к тангенциальным составляющим, соотношение которых удобно найти для вектора напряженности с помощью теоремы о циркуляции.

Выделим вблизи границы раздела небольшой прямоугольный контур ABCD (рис. 23.5). Выберем стороны АВ = CD = I так, что они параллельны границе раздела и находятся в разных магнетиках, а стороны ВС и DA бесконечно малы по сравнению со сторонами ВС Рис. 235

и DA. Тогда, пренебрегая в теореме о циркуляции интегралами по бесконечно малым сторонам, получим

откуда следует, что тангенциальная компонента вектора напряженности на границе раздела магнетиков остается непрерывной:

Выразив это соотношение через магнитную индукцию, получим, что тангенциальная компонента вектора магнитной индукции на границе раздела магнетиков претерпевает разрыв:

Таким образом, мы получили, что векторы напряженности и магнитной индукции претерпевают преломление при переходе из одной среды в другую. По аналогии с преломлением электрического поля в диэлектриках имеем закон преломления векторов напряженности магнитного поля и магнитной индукции:

Здесь а, — угол падения; а₂ — угол преломления. Формула показывает, что при переходе в магнетик с большей магнитной проницаемостью силовые линии напряженности и магнитной индукции удаляются от нормали.

Содержание

Условия для магнитного поля на границе раздела двух магнетиков
Ферромагнетики и их свойства
Вектор намагниченности на границе двух сред
Связь с автором (комментарии/рецензии к статье)
Оставить комментарий
💥 Видео

Видео:Урок 289. Магнитное поле в веществе. Магнитная проницаемость. Диа-, пара- и ферромагнетикиСкачать

Условия для магнитного поля на границе раздела двух магнетиков

Найдем связь между векторами поля (В и //) на границе раздела двух однородных магнетиков (магнитные проницаемости р, и р,) при отсутствии на границе тока проводимости.

Построим вблизи границы раздела магнетиков / и 2 прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом магнетике, другое — во втором (рис. 89). Основания ДS настолько малы, что в пределах каждого

из них вектор В одинаков. Согласно теореме Гаусса [см. (60.5)],

(нормали п и п’ к основаниям цилиндра направлены противоположно). Поэтому

Заменив, согласно В = р₀р// [см. (64.14)|, проекции вектора В проекциями вектора Н, умноженными на р₀р, получим

Вблизи границы раздела двух магнетиков / и 2 построим небольшой замкнутый прямоугольный контур ABCDA длиной /, ориентировав его так, как показано на рис. 90. Согласно теореме

(64.9) о циркуляции вектора Я,

(токов проводимости на границе раздела нет), откуда

(знаки интегралов по АВ и СП разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы). Поэтому

Заменив, согласно В = р₀рЯ |см. (64.14)], проекции вектора Я проекциями вектора Z?, деленными на р₀р, получим

Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая вектора В(В_п) и тангенциальная составляющая вектора Я (Я,) изменяются непрерывно (не претерпевают скачка), а тангенциальная составляющая вектора В(В_г) и нормальная составляющая вектора Я (//„) претерпевают скачок.

Из полученных условий (65.1)—(65.4) для составляющих векторов В и // следует, что линии этих векторов испытывают излом (преломляются). Как и в случае диэлектриков (см. § 21), можно

найти закон преломления линии В (а значит, и линий Н):

Из этой формулы следует, что, входя в магнетик с большей магнитной проницаемостью, линии В и Н удаляются от нормали.

Видео:магнитная защита. Векторы B и H на границе разделаСкачать

Ферромагнетики и их свойства

Особую группу магнетиков образуют ферромагнетики — твердые вещества, обладающие спонтанной намагниченностью даже при отсутствии внешнего магнитного поля, которая подвержена сильному влиянию внешних факторов — изменению температуры, магнитного поля, деформации.

К ферромагнетикам кроме основного их представителя — железа (от него и идет название «ферромагнетизм») — относятся, например, кобальт, никель, гадолиний, их сплавы и соединения.

В отличие от диа- и парамагнетиков (слабомагнитных веществ), для которых У от Я линейна |см. (64.11)], для ферромагнетиков (сильномагнитных веществ) эта зависимость сложная: вначале с возрастанием Н намагниченность J растет сначала быстро, затем медленнее, достигая магнитного насыщения J (рис. 91).

Подобный характер зависимости Уот Н можно объяснить тем, что по мере увеличения намагничивающего поля возрастает степень ориентации молекулярных магнитных моментов по полю. Однако этот процесс начнет замедляться, когда остается все меньше и меньше несориентирован- ных моментов, и наконец, когда все моменты будут ориентированы по полю, дальнейшее увеличение Н прекращается и наступает магнитное пасы щение.

Особенностью ферромагнетиков являются не только большие значения р (для железа р = 5000, для сплава супермаллоя — 800 000!), но и зависимость р от Н. Вначале р растет (рис. 92) с увеличением Н, затем, достигая максимума, начинает уменьшаться, стремясь в случае сильных полей

к I (р = —— = I + поэтому при У = У = const

с ростом // отношение

Ферромагнетики обладают еще одной особенностью: каждый из них обладает определенной температурой, называемой точкой Кюри, при нагревании выше которой ферромагнетик теряет магнитные свойства (превращается в обычный парамагнетик). Например, для железа точка Кюри находится при Т= 1042 К, для кобальта — 1400 К.

Спонтанное намагничивание находится в кажущемся противоречии с тем, что многие ферромагнитные материалы даже при температурах ниже точки Кюри не намагничены. По современным представлениям, ферромагнетик ниже точки Кюри разбивается на большое число малых макроскопических областей — доменов, самопроизвольно намагниченных до насыщения.

При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически и компенсируют друг друга, поэтому результирующий магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен. Внешнее магнитное поле ориентирует по полю магнитные моменты не отдельных атомов, как это имеет место в случае парамагнетиков, а целых областей спонтанной намагниченности, причем домены поворачиваются по полю скачком.

Помимо уже указанной выше нелинейной зависимости Уот /У (рис. 93) [а следовательно, и В от //: В — р₀(Я + У), см. (64.8)| эта зависимость определяется предысторией намагничивания. Если намагнитить ферромагнетик до насыщения (кривая /), то уменьшение Ус уменьшением Н происходит по кривой 2, а при Н = 0 ферромагнетик сохраняет остаточное намагничивание У . С наличием У_ос связано существование постоян-

пых магнитов. Намагничивание обращается в нуль под действием поля Н_с, имеющего направление, противоположное полю, вызвавшему намагничивание. Напряженность Н_с называют коэрцитивной силой. При дальнейшем изменении // намагниченность изменяется в соответствии с замкнутой петлей, называемой петлей гистерезиса.

Гистерезисные петли для различных ферромагнетиков — разные. Мягкие ферромагнетики характеризуются малой коэрцитивной силой //

(узкой петлей гистерезиса) (рис. 94, а), жесткие — большой // (широкой петлей гистерезиса) (рис. 94, б).

Жесткие ферромагнетики (например, углеродистые и вольфрамовые стали) применяются для изготовления постоянных магнитов, а мягкие (например, мягкое железо, сплав железа с никелем) — для изготовления сердечников трансформаторов.

Видео:2.5 Граничные условия для векторов поля на поверхности раздела средСкачать

Вектор намагниченности на границе двух сред

Библиографическая ссылка на статью:
Чуев А.С. О новых подходах в описании стационарного магнитного поля внутри и на границе раздела двух сред // Современные научные исследования и инновации. 2015. № 7. Ч. 1 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2015/07/56905 (дата обращения: 24.01.2022).

Магнитное поле принято описывать тремя магнитными векторами, соотношение которых обычно приводят в форме:

где: – вектор магнитный индукции; – магнитная постоянная; – вектор напряженности магнитного поля; – вектор намагниченности вещественной среды. Каждому их трех магнитных векторов приписывают свое особенное поле.Намагниченность считают присутствующей в веществе (в магнетиках), магнитную индукцию – присутствующей везде, а вектор считают мнимым вспомогательным вектором, «не имеющим сколько-нибудь глубокого физического смысла» [1, стр.184].

В работах автора 2 показывается, что соотношение (1) логичнее и правильнее представлять в форме сложения векторов

В этом случае проявляется совсем иной смысл этого соотношения. Вектор оказывается составным и вспомогательным, а векторы Н и J становятся исходными (первичными), о чем поясняется далее.
Из практики магнетизма известно, что вектор Н образуется токами проводимости и только ими, поскольку циркуляция этого вектора по замкнутому контуру всегда равна сумме токов проводимости.
Поскольку вектор Н совпадает по размерности с вектором J , то можно предположить, что этот вектор тоже есть своеобразная намагниченность – намагниченность свободного пространства (вакуума). Из этого предположения с учетом формулы (2) следует, что отношение тоже представляет собой намагниченность , только суммарную. Однако не все согласны с таким подходом из-за его несоответствия устоявшимся терминам и представлениям.
Подтверждение авторской позиции и важность правильного представления о том, какие из трех магнитных векторных величин являются первичными, покажем рассмотрением двух примеров из учебника Иродова [1, (примеры 7.6 и 7.3)].
На рис. 1 приводятся рисунки из примера с задачей определения индукции магнитного поля в поперечном щелевом зазоре кольцевого магнита.

В данном примере учебника не только утверждается наличие вектора Н в любой точке вещества магнита, но и показывается направленность этого вектора противоположная вектору В .
Присутствие вектора J в любой точке вещества магнита вполне понятно, но наличие там противоположно направленного вектора Н представляется ничем не обоснованным утверждением. Приводимое в учебнике решение [1, стр. 200] основано, по мнению автора, на неправомерном использовании теоремы о циркуляции вектора Н в отсутствии токов проводимости

Из этого уравнения получают следующие решения:

В отсутствии воздушного зазора напряженность полностью исчезает и становится нулевой.
Интересно найти ответ на вопрос: что собой физически представляет напряженность , направленная против намагниченности J . Ведь при первичном намагничивании магнита поле напряженность Н направлена так же как и индукция В и они связаны известной формулой

В литературе по магнетизму напряженность принято считать особым размагничивающим полем, которое возникает в кольцевом магните при наличии в нем щелевого зазора. Размагничивающее поле появляется и в магнитах иной формы сразу же после размыкания магнитопровода цепи их первоначального намагничивания [5]. Опыт показывает, что напряженность вводимого расчетного размагничивающего поля пропорциональна намагниченности материала магнита и зависит от его геометрической формы.

Здесь N – коэффициент размагничивания, зависящий от формы намагничиваемого тела и его ориентации относительно внешнего магнитного поля; для магнита, имеющего форму шара N = 1/2 [5].
По мнению автора, размагничивающее поле не мнимое. Это вполне реальное поле, которое существует как суммарное обратное магнитное поле элементарных магнитных диполей, из которых состоит магнит. Что собой представляет каждый элементарный магнитный диполь или домен, имеющий прямое (внутреннее, более сильное) и обратное (внешнее, значительно менее сильное) магнитное поле, можно понять из приводимых изображений рис. 2.

Убедительным подтверждением наличия в магнетиках, наряду с прямым полем и обратного (размагничивающего) поля, служит опыт по втягиванию в катушку с током связанных и свободных от связи друг с другом намагничиваемых проволочных стержней (рис. 3) [6, стр. 216].

Этот опыт можно интерпретировать так: в стержневой связке намагничиваемых проволок их прямое поле намагниченности ослабляется воздействием обратного поля соседних проволок, поэтому силы электромагнита недостаточно для втягивания всего пучка. В состоянии проволок порознь, указанное ослабление прямого поля намагниченности каждой из проволок становится меньше, и тогда они оказываются способны к втягиванию в электромагнит.
Поскольку излагаемый нами подход отвергает соотношение (3), то возникает вопрос – как по другому можно связать индукцию В в зазоре и намагниченность J материала магнита? Для кольцевых и полузамкнутых магнитопроводов с небольшими воздушными зазорами такая возможность есть. Логически оправдано определять интенсивность магнитного поля в небольшом воздушном зазоре как общую с кольцевым магнитом намагниченность , но уменьшенной величины, определяемой из условия возрастания рассматриваемого объема при сохранении числа вещественных магнитных диполей, находящихся в теле магнита. Вытекающее из этого условия расчетное соотношение для индукции В , определяемой в воздушном зазоре (см. рис.1) при неизменности поперечного сечения S кольцевого магнита, следующее

Данное соотношение эквивалентно соотношению, приводимому в учебнике Иродова

Этот пример говорит о том, что магнитные дипольные моменты , принадлежащие скоплениям намагниченного вещества отдельных молекул, атомов и элементарных частиц, которые обладают способностью создавать в окружающем пространстве внешнее магнитное поле, можно считать своеобразными «магнитными зарядами» с дипольной формой магнитного поля.
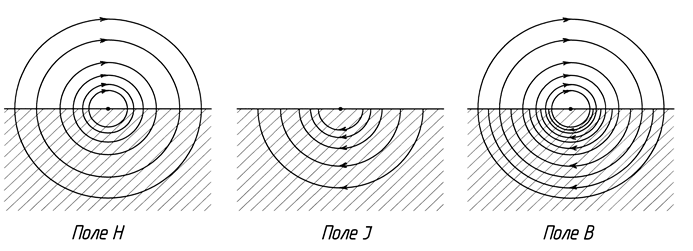
Рассмотрим другой пример из того же учебника, характерный ошибочным изображением полей магнитных векторов. Иродов приводит (ошибочное, на наш взгляд) изображение полей В и Н , создаваемых прямым длинным тонким проводником с током, расположенным в плоскости, отделяющей пространство, заполненное непроводящим магнетиком с проницаемостью , от вакуума. Изображение рисунка данного примера приведено на рис. 4.

Ошибочность рис. 4 состоит в том, что поле В показано одинаковым как внутри магнетика, так и в вакууме, а результирующее (по Иродову) поле Н внутри магнетика показано ослабленным, хотя приводимый на рисунке магнетик явно не подходит под диамагнетик. Известен закон Био-Савара-Лапласа, по которому поле В обязано быть различным в вакууме и в магнетике. Наличие среды в этом законе учитывается присутствием . Поскольку в магнетике поле В обязательно будет усиленным или ослабленным по сравнению с вакуумом, то оно неизбежно оказывается составным, представляя собой сумму двух исходных полей: первичного поля Н от тока проводимости и вторичного поля J от реакции магнетика на это первичное поле.
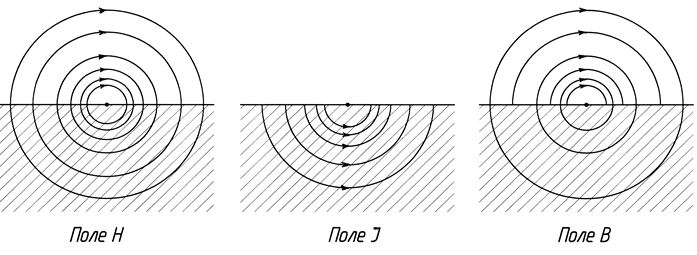
Правильное изображение данного примера, по мнению автора, должно соответствовать изображениям рис. 5 и рис. 6. Для большей наглядности приводятся два варианта: с диамагнетиком и пара- или ферромагнетиком.

Рис. 6. Магнитные поля от проводника с током на границе вакуум-диамагнетик

На изображениях рис. 5 и рис. 6 поле В (в системе СИ, ) имеет естественный вид суммарного поля двух исходных полей, соответствуя соотношению (2). Безусловная верность данных изображений видится в том, что они соответствуют принципу суперпозиции – методологически верному и всеобщему.

Автор обычно встречает следующее возражение, подвергающее сомнению правильность изображений, приведенных рис. 5 и рис. 6. На этих рисунках, мол, линии поля вектора В на границе двух сред не непрерывны, поэтому дивергенция вектора В не равна нулю, что противоречит известному четвертому уравнению Максвелла.
Максвелл жил давно и в его время о магнетизме многое чего не было известно. Сегодня мы знаем многократно проверенную опытом теорему о циркуляции вектора Н , знаем о наличии виртуальных частиц физического вакуума, ушло в небытие представление о разнополярных магнитных зарядах. Так что новые знания диктуют формирование новых представлений, быть может, иногда и противоречащих базовым, в определенный момент времени, знаниям.
Рассмотрим наглядный пример, представленный на рис. 7. Имеется катушка индуктивности с током, внутрь катушки вставлен стержень из ферромагнитного материала с большой магнитной восприимчивостью и способностью к остаточной намагниченности. При наличии тока в катушке общее магнитное поле внутри стержня представлено векторами Н (от тока катушки) и J ( намагниченность вещества магнита). Очевидно, что вектор выступает здесь в качестве суммарного вектора, поскольку он определяется в основном величиной намагниченности J . Считать в этом случае суммарным вектором напряженность Н – означает противоречить элементарной логике. Естественно, что все три магнитных вектора имеют одинаковую направленность.

Чтобы передать достаточно верное представление о соотношении средних значений модуля магнитных векторов внутри различных магнетиков на рис. 8 приведены диаграммы, поясняющие различные возможные ситуации.

Изображения рис. 8 наглядно и убедительно иллюстрируют – чем отличаются отклики (вектор J ) в различных магнетиках на первичный вектор Н . Этот отклик в различных магнетиках различен по величине и направлению. Вполне очевидно, что вектор присутствует в каждом изображении рис. 8 как составной результирующий вектор и этот вектор никак не может быть первичным. Вполне очевидно, что в варианте с ферромагнетиком результирующее магнитное поле формируется, в основном, за счет реакции магнетика.
Осветим теперь вопрос поведения магнитных векторов на границе двух сред. Кое что можно было понять уже из рис. 5. Очевидно, что вектор J не должен выходить за пределы магнетика согласно своему определению в качестве вектора вещественной намагниченности .
Вектор Н существует только при наличии токов проводимости. С выключением токов он должен прекращать свое существование. Представление о том, что этот вектор (поле этого вектора) не зависит от среды подтверждается многими исследователями и учебниками, среди них: С.Г. Калашников [6, стр. 212], А.Н. Матвеев [7, стр. 271], И.Е. Тамм [8, стр. 339].
Вектор B в качестве суммарного вектора может показываться всегда, но показывать этот вектор и одновременно его составляющие: векторы Н и J , следует с обязательными оговорками, поскольку векторы Н и J как бы исчезают с появлением вектора В . Нельзя также забывать, что последний участвует с размерностным сомножителем μ ₀ . При отсутствии одного какого-либо из первичных векторов Н или J , вектор B (точнее ) оставшемуся вектору будет обязательно параллелен и одинаково с ним направлен.
К сказанному о магнитных полях и векторах следует добавить, что все намагниченные тела создают внешнее (вне своего тела) магнитное поле, которое также принято обозначать вектором В . На рис. 8 это поле не показано, но оно хорошо видно на рис. 2.
Представим себе рис. 8 с выключенным током в катушке и остаточной намагниченностью стержня, который создает внешнее дипольное магнитное поле. Поле вектора Н будет отсутствовать в силу отсутствия тока в катушке. Поле вектора намагниченности J мы обязаны сохранить только внутри ферромагнетика, а поле вектора В будем считать присутствующим внутри и вне стержня с линиями, не претерпевающими разрывов на торцевых поверхностях стержня (из условия ). Однако при очевидных разрывах поля вектора J на торцах стержня возникает парадокс, заключающийся в том, что условие (2) становится невыполнимым.
Чтобы разрешить данную проблемную ситуацию, внутрь и вне магнита обычно вводят дополнительное векторное поле с размерностью напряженности . Это поле никак не связано с силой тока и числом витков катушки, а определяется лишь соотношением геометрических размеров магнита и воздушного зазора между его полюсами (см. рис. 1). Внутри магнита это дополнительное поле считают направленным против вектора намагниченности J , а вне магнита считают совпадающим с вектором В . До кучи принимается еще одно допущение – о нулевом значении циркуляция вектора напряженности этого дополнительного поля.
Все сказанное имело определенное логичное объяснение при господстве в магнетизме представлений о магнитных зарядах , возникающих на магнитных полюсах постоянных магнитов и создающих это дополнительное магнитное поле. Когда же представления о магнитных зарядах «канули в лету», то ситуация стала необъяснимой и даже абсурдной. Разрывы вектора J на торцах намагниченного стержня, объясняемые прежде скоплением магнитных зарядов и скачком на них вектора Н , объяснять стало нечем. Обратное дипольное поле, приводимое и рассмотренное нами выше (см. рис. 2 и рис. 3) на эту роль никак не годится, в силу его слабости по сравнению с полем прямой намагниченности .
По мнению автора, ситуация становится разрешимой, если внутри постоянных магнитов перестать видеть поле вектора Н . Следует воспринимать это поле создаваемым исключительно токами проводимости. Тогда в теле магнита остается только поле вектора намагниченности J , неотличимое от соотношения , а вне тела магнита остается то же самое поле, выражаемое отдельным вектором В или тем же самым отношением . Данное поле вне магнита можно принимать и за поле вектора Н , поскольку внешние поля, создаваемые магнитами и токами проводимости ничем не отличаются.
Теперь мы вплотную подошли к тому, чтобы разобраться с соотношением внутри и вне магнетиков. Особенно интересен вопрос о том, как изменяется это соотношение на границе двух сред
В настоящее время обыкновенно считают, что в изотропных магнетиках и в вакууме существуют оба вектора В и Н , которые имеют одинаковую направленность (есть и исключения, пример рис. 1). При пересечении границы двух сред не по нормали к преграде оба эти вектора (их линии) испытывают преломление под одинаковым углом (рис. 9) [1]. При этом, силовые линии вектора В считаются непрерывными, а линии вектора Н обычно изображают частично прерывающимися или «возникающими» на границе двух сред.
Считают также, что преломление векторов В и Н на границе двух сред подчиняется закону тангенсов [9]. Однако, как отмечено в авторской работе [10], в электродинамике этот «закон» входит в противоречие с законом преломления оптических лучей (законом синусов), поскольку векторы Е и Н ориентированы перпендикулярно направлению распространения луча.

Наряду с парадоксом двух разных законов преломления магнитных векторов можно отметить другие неясности и парадоксы. Если вектор Н не зависит от параметров среды, то непонятно каким образом он может испытывать преломление на границе двух сред? Если вектор Н определяется лишь токами проводимости, то каким образом линии этого вектора могут прерываться и возникать на границе двух сред?
Приступая к рассмотрению поведения магнитных векторов В и Н на границе двух сред необходимо также отметить, что в сравнении с аналогичным примером для электрических векторов, это рассмотрение оказывается значительно более сложным и запутанным,. Во-первых, на беспристрастное рассмотрение этой темы оказывают сильное давление устоявшиеся представления о нулевой дивергенции вектора В и о самой дивергенции [12]. Во-вторых, магнитное поле вихревое, а простые наглядные изображения и опытные данные, иллюстрирующие принцип суперпозиции, обладают хорошей наглядностью при использовании первичными однородных полей. В третьих, векторное поле Н обычно обнаруживается и экспериментально измеряется по значению магнитной индукции В или магнитного потока Ф, а векторное поле J внутри магнетиков поддается только вычислению. Общая теория вычисления параметров магнитного поля в пространстве, окружающем намагниченные тела сложной формы, пока не разработана.
Все вышеотмеченное позволило автору увидеть и предложить новую модель, описывающую механизм поведение магнитных векторов на границе двух сред. Данная модель представлена на рис. 10 и рис. 11. По аналогии с ранее предложенной моделью преломления линий суммарного электрического вектора Е на границе двух сред [13], в этой модели, иллюстрирующей механизм преломления линий вектора В , определяющую роль играет состояние этой самой границы двух сред. Только роль связанных зарядов, ответственных в электростатике за преломление линий вектора Е , здесь выполняет поверхностный ток намагничивания.
Поверхностный ток намагничивания, определяемый составляющей внешнего магнитного поля параллельной плоскости раздела двух сред [], обозначен на приводимых рисунках уходящими от нас стрелками. Плоскость раздела на рисунках образована двумя средами. Нижняя среда представляет собой вакуум с , а верхняя среда вещественная имеющая > 1.

Представленная на рис. 10 модель выполнена для упрощения неполной. Здесь умышленно не показано влияние намагниченной вещественной среды на первичное внешнее поле в примыкающем к веществу свободном пространстве. Обозначенное воздействие намагниченной вещественной среды на магнитное поле примыкающего свободного пространства, включая влияние поверхностного тока намагничивания, рассмотрено далее на рис. 11.
Практика показывает, что поляризуемые или намагничиваемые вещества деформируют первичное возбуждающее поле в примыкающем свободном пространстве. Визуально это проявляется в виде эффекта вздыбливания ворсинок на поверхностях поляризованных тел и ориентации «ёжиком» железных опилок на поверхности намагниченных тел, что говорит о перпендикулярном (или почти перпендикулярном) направлении близ расположенных силовых линий внешнего поля, как электрического, так и магнитного, относительно поверхности поляризуемых или намагничиваемых тел.
Кроме этого, в реальности имеет место явное усиление внешнего поля, примыкающего к полюсам намагничиваемых или поляризуемых тел (10, стр.80). Как происходит изменение осевой намагниченности (поля, определяемого соотношением ) в цилиндрическом стержне вблизи его торцов при нормальном подходе линий поля к плоскости торца показано в работах [12, 13]. Однако более сложен и интересен вопрос о поведении магнитных векторов на границе двух сред, при подходе линий поля под углом к нормали плоскости раздела двух сред.
Все отмеченные выше факты и факторы послужили основанием для создания нового видения механизма преломления магнитных силовых линий и вектора В на плоской границе двух сред. Модель этого механизма в полной форме приведена на рис. 11. По этой модели внешнее магнитное поле, представленное вектором , усиливается внутри пара – или ферромагнетика до значения

Можно эту формулу представлять и в упрощенном виде , различие для ферромагнитных сред с >>1 будет совсем незначительным.

Очевидно, что усиленное поле внутри ферромагнетика приводит к появлению усиленного магнитного поля и в примыкающем пространстве. На рис. 11 это поле обозначено пунктирным вектором, однонаправленным и равновеликим с вектором .
По рис. 11 видно, что различие в направленности суммарных векторов по обе стороны от границы двух сред возникает, главным образом, из-за разнонаправленных составляющих магнитного поля от молекулярных токов на границе двух сред. Это аналогично воздействию на преломление вектора Е связанных зарядов на границе двух диэлектриков.
С учетом магнитного поля от молекулярных токов на границе двух сред, общая формула, определяющая суммарное поле в магнетике, имеет вид

С учетом «намагничивания» магнетиком примыкающего пространства, которое принято приписывать свойству , аналогичная формула, определяющая суммарное магнитное поле вблизи магнетика, имеет вид

Как видим, две последние формулы различаются лишь составляющими и , принадлежащими полю, создаваемому плоскостью молекулярных токов. Эти составляющие и являются главными в механизме преломления вектора В на границе двух сред, чего до сих пор не замечалось.

На базе новых представлений о физическом содержании и соотношении магнитных векторов предложена новая модель, объясняющая причину и механизм преломления вектора магнитной индукции на границе двух сред.

Библиографический список

Иродов И.Е. Электромагнетизм. Основные законы. Изд. 4-е испр.– М.: БИНОМ. Лаборатория знаний. 2003. – 320 с.
Чуев А.С. Магнитное поле – какие векторы первичны и что мы измеряем? «Законодательная и прикладная метрология». №6-2012. С. 45-48.
Чуев А.С. О формульном и наглядном соотношении магнтитных векторных величин и изображении их полей. Научно-техническая библиотека. Электронный ресурс. URL: http://www.sciteclibrary.ru/rus/catalog/pages/12150.html (дата обращения 26.06.2012 г.).
Чуев А.С. О различиях и единстве магнитных векторных величин. «Инженерно-физические проблемы новой техники». Сборник материалов XI Всероссийского совещания-семинара, МГТУ им. Н.Э. Баумана 15-17 апреля 2014 г. Стр. 40-43. (Электронный вариант URL: http://www.sciteclibrary.ru/rus/catalog/pages/13871.html, дата обращения 16.06.2014).
Арнольд Р.Р. Расчет и проектирование магнитных систем с постоянными магнитами. – М.: Энергия. 1969. 184 с.
Калашников С.Г. Электричество: Учебное пособие. 5-е изд. испр. и доп. – М., Наука. 1985. – 576 с.
Матвеев А.Н. Электричество и магнетизм: Учеб. пособие. – М.: Высш. школа. 1983. – 463 с.
Тамм И.Е. Основы теории электричества. Учеб. пособие для вузов. – 11-е изд., испр. и доп. – М.: ФИЗМАТЛИТ, 2003. – 616 с.
Савельев И.В. Курс общей физики: В 5 кн.: Кн. 2: Электричество и магнетизм: Учеб. Пособие для втузов. – М.: «Издат. АСТ». 2004. -334 с.
Чуев А.С. О новых подходах в описании стационарного электрического поля внутри диэлектрических сред и на границе их раздела. Инженерный журнал: наука и инновации, 2014, вып. 6. URL: http://engjournal.ru/catalog/fundamentals/physics/1325.html (дата обращения 20.11.2014).
Чуев А.С. О понятии и толкованиях дивергенции поля векторных величин. URL: http://mail.sciteclibrary.ru/rus/catalog/pages/12428.html (дата обращения 20.11.2014).
Чуев А.С. Формульные и наглядные соотношения электрических и магнитных векторных величин в новом представлении. Материалы Восьмой Всерос. конференция «Необратимые процессы в природе и технике». 27-29 января 2015 г.Часть III. М., МГТУ им. Н.Э. Баумана. Стр. 178-182.
Чуев А.С. Уточненные формульные и наглядные соотношения электрических и магнитных векторных величин в новом представлении. Матер. 8-й Всерос. конференции «Необратимые процессы в природе и технике». 27-29 января 2015 г.Часть III. М., МГТУ им. Н.Э. Баумана. Стр. 183-187.

Количество просмотров публикации: Please wait