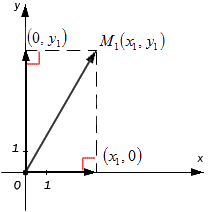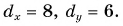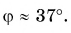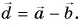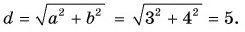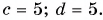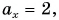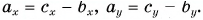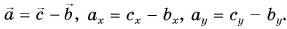 |
| рис. 1 |
- Формула вычисления проекции вектора на вектор
- Примеры задач на проекцию вектора
- Примеры вычисления проекции вектора для плоских задач
- Примеры вычисления проекции вектора для пространственных задачи
- Проекция вектора на ось и числовая проекция
- Числовая проекция вектора на ось
- Проекция вектора на ось в физике — формулы и определения с примерами
- Как определяют проекцию вектора на ось
- Можно ли найти модуль и направление вектора по его проекциям на координатные оси
- Пример №1
- Пример №2
- 🎬 Видео
Видео:Построение проекции вектора на осьСкачать

Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
| Пр b a = | a · b |
| | b | |
Видео:Векторные величины Проекция вектора на осьСкачать

Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
| b | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
Найдем проекцию вектора a на вектор b
| Пр b a = | a · b | = | 11 | = 2.2 |
| | b | | 5 |
Примеры вычисления проекции вектора для пространственных задачи
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
| b | = √ 4 2 + 2 2 + 4 2 = √ 16 + 4 + 16 = √ 36 = 6
Найдем проекцию вектора a на вектор b
| Пр b a = | a · b | = | 12 | = 2 |
| | b | | 6 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Урок 9. Проекции вектора на координатные осиСкачать

Проекция вектора на ось и числовая проекция
Ось – это направление. Значит, проекция на ось или на направленную прямую считается одним и тем же. Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.
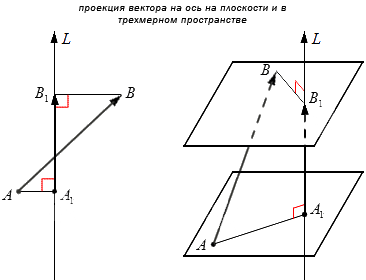
Если имеем ось L и ненулевой вектор A B → , то можем построить вектор A 1 B 1 ⇀ , обозначив проекции его точек A 1 и B 1 .
A 1 B → 1 будет являться проекцией вектора A B → на L .
Проекцией вектора на ось называют вектор, начало и конец которого являются проекции начала и конца заданного вектора. n p L A B → → принято обозначать проекцию A B → на L . Для построения проекции на L опускают перпендикуляры на L .
Пример проекции вектора на ось.
На координатной плоскости О х у задается точка M 1 ( x 1 , y 1 ) . Необходимо построить проекции на О х и О у для изображения радиус-вектора точки M 1 . Получим координаты векторов ( x 1 , 0 ) и ( 0 , y 1 ) .
Если идет речь о проекции a → на ненулевой b → или проекции a → на направление b → , то имеется в виду проекция a → на ось, с которой совпадает направление b → . Проекция a → на прямую, определяемая b → , имеет обозначение n p b → a → → . Известно, что когда угол между a → и b → , можно считать n p b → a → → и b → сонаправленными. В случае, когда угол тупой, n p b → a → → и b → противоположно направлены. В ситуации перпендикулярности a → и b → , причем a → — нулевой, проекция a → по направлению b → является нулевым вектором.
Видео:Как записать проекцию вектора на оси координат - bezbotvyСкачать

Числовая проекция вектора на ось
Числовая характеристика проекции вектора на ось – числовая проекция вектора на заданную ось.
Числовой проекцией вектора на ось называют число, которое равно произведению длины данного вектора на косинус угла между данным вектором и вектором, который определяет направление оси.
Числовая проекция A B → на L имеет обозначение n p L A B → , а a → на b → — n p b → a → .
Исходя из формулы, получим n p b → a → = a → · cos a → , b → ^ , откуда a → является длиной вектора a → , a ⇀ , b → ^ — угол между векторами a → и b → .
Получим формулу вычисления числовой проекции: n p b → a → = a → · cos a → , b → ^ . Она применима при известных длинах a → и b → и угле между ними. Формула применима при известных координатах a → и b → , но имеется ее упрощенный вид.
Узнать числовую проекцию a → на прямую по направлению b → при длине a → равной 8 и углом между ними в 60 градусов. По условию имеем a ⇀ = 8 , a ⇀ , b → ^ = 60 ° . Значит, подставляем числовые значения в формулу n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .
Ответ: 4.
При известном cos ( a → , b → ^ ) = a ⇀ , b → a → · b → , имеем a → , b → как скалярное произведение a → и b → . Следуя из формулы n p b → a → = a → · cos a ⇀ , b → ^ , мы можем найти числовую проекцию a → направленную по вектору b → и получим n p b → a → = a → , b → b → . Формула эквивалента определению, указанному в начале пункта.
Числовой проекцией вектора a → на ось , совпадающей по направлению с b → , называют отношение скалярного произведения векторов a → и b → к длине b → . Формула n p b → a → = a → , b → b → применима для нахождения числовой проекции a → на прямую, совпадающую по направлению с b → , при известных a → и b → координатах.
Задан b → = ( — 3 , 4 ) . Найти числовую проекцию a → = ( 1 , 7 ) на L .
Решение
На координатной плоскости n p b → a → = a → , b → b → имеет вид n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 , при a → = ( a x , a y ) и b → = b x , b y . Чтобы найти числовую проекцию вектора a → на ось L , нужно: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · ( — 3 ) + 7 · 4 ( — 3 ) 2 + 4 2 = 5 .
Ответ: 5.
Найти проекцию a → на L , совпадающей с направлением b → , где имеются a → = — 2 , 3 , 1 и b → = ( 3 , — 2 , 6 ) . Задано трехмерное пространство.
Решение
По заданным a → = a x , a y , a z и b → = b x , b y , b z вычислим скалярное произведение: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Длину b → найдем по формуле b → = b x 2 + b y 2 + b z 2 . Отсюда следует, что формула определения числовой проекции a → будет: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .
Подставляем числовые значения: n p L a → = n p b → a → = ( — 2 ) · 3 + 3 · ( — 2 ) + 1 · 6 3 2 + ( — 2 ) 2 + 6 2 = — 6 49 = — 6 7 .
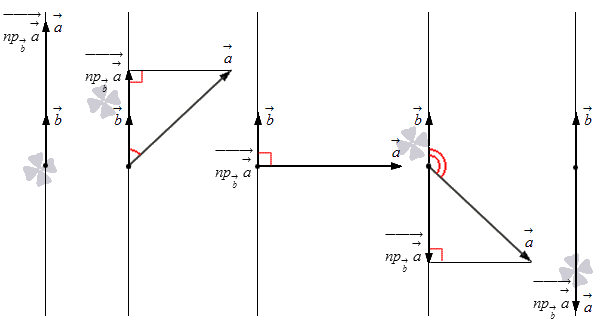
Просмотрим связь между a → на L и длиной проекции a → на L . Начертим ось L , добавив a → и b → из точки на L , после чего проведем перпендикулярную прямую с конца a → на L и проведем проекцию на L . Существуют 5 вариаций изображения:
Первый случай при a → = n p b → a → → означает a → = n p b → a → → , отсюда следует n p b → a → = a → · cos ( a , → b → ^ ) = a → · cos 0 ° = a → = n p b → a → → .
Второй случай подразумевает применение n p b → a → ⇀ = a → · cos a → , b → , значит, n p b → a → = a → · cos ( a → , b → ) ^ = n p b → a → → .
Третий случай объясняет, что при n p b → a → → = 0 → получаем n p b ⇀ a → = a → · cos ( a → , b → ^ ) = a → · cos 90 ° = 0 , тогда n p b → a → → = 0 и n p b → a → = 0 = n p b → a → → .
Четвертый случай показывает n p b → a → → = a → · cos ( 180 ° — a → , b → ^ ) = — a → · cos ( a → , b → ^ ) , следует n p b → a → = a → · cos ( a → , b → ^ ) = — n p b → a → → .
Пятый случай показывает a → = n p b → a → → , что означает a → = n p b → a → → , отсюда имеем n p b → a → = a → · cos a → , b → ^ = a → · cos 180 ° = — a → = — n p b → a → .
Числовой проекцией вектора a → на ось L , которая направлена как и b → , имеет значение:
- длины проекции вектора a → на L при условии, если угол между a → и b → меньше 90 градусов или равен 0: n p b → a → = n p b → a → → с условием 0 ≤ ( a → , b → ) ^ 90 ° ;
- ноля при условии перпендикулярности a → и b → : n p b → a → = 0 , когда ( a → , b → ^ ) = 90 ° ;
- длины проекции a → на L , умноженной на -1, когда имеется тупой или развернутый угол векторов a → и b → : n p b → a → = — n p b → a → → с условием 90 ° a → , b → ^ ≤ 180 ° .
Дана длина проекции a → на L , равная 2 . Найти числовую проекцию a → при условии, что угол равен 5 π 6 радиан.
Решение
Из условия видно, что данный угол является тупым: π 2 5 π 6 π . Тогда можем найти числовую проекцию a → на L : n p L a → = — n p L a → → = — 2 .
Дана плоскость О х y z с длиной вектора a → равной 6 3 , b → ( — 2 , 1 , 2 ) с углом в 30 градусов. Найти координаты проекции a → на ось L .
Решение
Для начала вычисляем числовую проекцию вектора a → : n p L a → = n p b → a → = a → · cos ( a → , b → ) ^ = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .
По условию угол острый, тогда числовая проекция a → = длине проекции вектора a → : n p L a → = n p L a → → = 9 . Данный случай показывает, что векторы n p L a → → и b → сонаправлены, значит имеется число t , при котором верно равенство: n p L a → → = t · b → . Отсюда видим, что n p L a → → = t · b → , значит можем найти значение параметра t : t = n p L a → → b → = 9 ( — 2 ) 2 + 1 2 + 2 2 = 9 9 = 3 .
Тогда n p L a → → = 3 · b → с координатами проекции вектора a → на ось L равны b → = ( — 2 , 1 , 2 ) , где необходимо умножить значения на 3. Имеем n p L a → → = ( — 6 , 3 , 6 ) . Ответ: ( — 6 , 3 , 6 ) .
Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.
Видео:Известно, что проекция вектора начальной скорости тела на ось xСкачать

Проекция вектора на ось в физике — формулы и определения с примерами
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
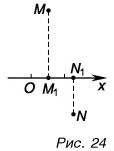
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Как определяют проекцию вектора на ось
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
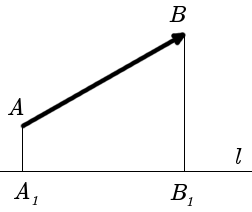
На рисунке 25 проекция вектора 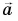
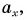
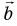
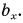
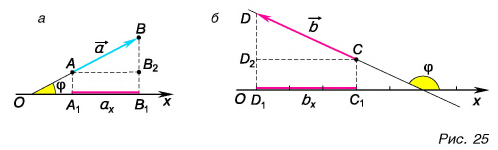
Проекция 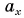
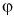
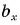
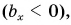
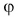
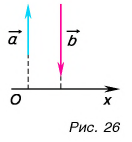
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 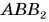
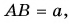
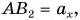
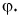
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
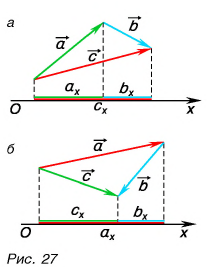
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 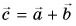
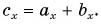
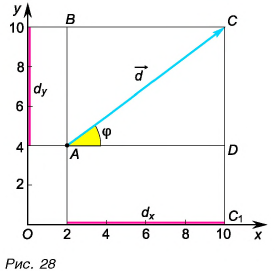
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
Рассмотрим вектор 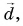
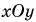
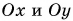
Модуль вектора 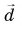
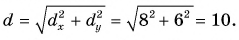
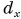
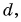
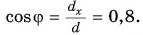
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
Вектор в пространстве определяется тремя проекциями: 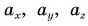
Главные выводы:
- Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
- Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
- Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
- Проекция суммы векторов на ось равна сумме их проекций на эту ось.
Пример №1
1. Определите сумму и разность взаимно перпендикулярных векторов 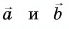
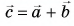
Решение
Сумму векторов 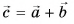
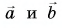
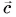
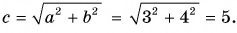
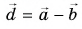
Модуль вектора 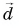
Ответ:
Пример №2
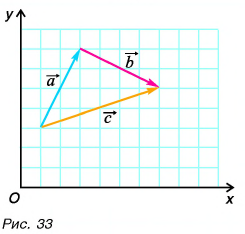
Выразите вектор 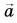
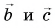
Решение
По правилу треугольника находим: 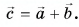
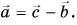
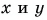
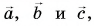
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎬 Видео
Проекция перемещения на ось XСкачать

Проекция вектора на вектор.Скачать

Проекция вектора на ось.Скачать

Основы кинематики. Тема 3. Проекция вектора на осьСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Урок 10. Действия над проекциями вектораСкачать

Как проецировать вектор сил на оси | ЕГЭ Физика | Николай Ньютон. ТехноскулСкачать

Урок 4. Кинематика: Проекции вектора перемещения на оси координат. Задачи / Репетитор по физике ЕГЭСкачать

Видеоурок 1 Векторы и их проекцииСкачать

Как построить проекцию вектора?Скачать

Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

Проекция вектора на ось #егэ #физика_огэ #физикаегэ #школа #mathsСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать