- Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
- Полнота
- Существование и единственность представления Теорема Жегалкина: Каждая булева функция единственным образом представляется в виде полинома Жегалкина. Заметим, что различных булевых функций от $n$ переменных $2^ $ штук. При этом конъюнкций вида $x_ ldots x_ $ существует ровно $2^n$, так как из $n$ возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит $0$ или $1$, то есть существует $2^ $ различных полиномов Жегалкина от $n$ переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него . Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом. Построение полинома Жегалкина Существует несколько способов построения полинома Жегалкина. По таблице истинности Пусть для функции $f(x_1,x_2,dots,x_n)$ задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что $ a oplus 1 = bar $, а $ a oplus 0 = a$. За каждую подстановку находим только один коэффициент. Пример: Дана функция $f(x_1,x_2,x_3,x_4)$ и её таблица истинности: $x_1$ $x_2$ $x_3$ $x_4$ $f(x_1,x_2,x_3,x_4)$ 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 0 1 0 0 1 0 1 1 1 1 1 0 0 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 0 Построим для неё полином Жегалкина: $f(x_1,x_2,x_3,x_4) = a_ oplus a_ x_1 oplus a_ x_2 oplus a_ x_3 oplus a_ x_4 oplus a_ x_1 x_2 oplus a_ x_1 x_3 oplus a_ x_1 x_4 oplus \ oplus a_ x_2 x_3 oplus a_ x_2 x_4 oplus a_ x_3 x_4 oplus a_ x_1 x_2 x_3 oplus a_ x_1 x_2 x_4 oplus \ oplus a_ x_1 x_3 x_4 oplus a_ x_2 x_3 x_4 oplus a_ x_1 x_2 x_3 x_4$ Так как $f(0,0,0,0) = 0$, то $a_ = 0$. Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы: $f(1,0,0,0) = a_ oplus a_ = 1 Rightarrow a_ = 1$ $f(0,1,0,0) = a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(0,0,1,0) = a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(0,0,0,1) = a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(1,1,0,0) = a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$ $f(1,0,1,0) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$ $f(1,0,0,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$ $f(0,1,1,0) = a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 1$ $f(0,1,0,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(0,0,1,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(1,1,1,0) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$ $f(1,1,0,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$ $f(1,0,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$ $f(0,1,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$ $f(1,1,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus \ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$ Таким образом, полином Жегалкина выглядит так: $f(x_1,x_2,x_3,x_4) = x_1 oplus x_1 x_3 oplus x_1 x_4 oplus x_2 x_3 oplus x_2 x_3 x_4 oplus x_1 x_2 x_3 x_4$ Преобразование дизъюнктивной нормальной формы Этот способ основан на том, что $ X oplus 1 = bar $. Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило Де-Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю , а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу: $ A lor B = AB oplus A oplus B $ $ (1) $. Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ. Пример: Дана функция в ДНФ $ f(x_1,x_2,x_3,x_4) = (x_1 land x_2 land neg x_3 land x_4) lor (neg x_1 land neg x_4) lor (x_1 land x_2) lor x_2 $, построим полином Жегалкина. Запишем функцию так: $f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 + neg x_1 neg x_4 + x_1 x_2 + x_2$; Сгруппируем слагаемые и воспользуемся преобразованием (1): $f(x_1,x_2,x_3,x_4) = (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_1 x_2 neg x_3 x_4 neg x_1 neg x_4) + (x_1 x_2 oplus x_2 oplus oplus x_1 x_2 x_2)$ Воспользуемся свойствами конъюнкции $A land A = A$ и $neg A land A = 0$, а также тем, что $A oplus A = 0$, и упростим выражение: $f(x_1,x_2,x_3,x_4) = (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4) + x_2$ Ещё раз воспользуемся преобразованием (1): $f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_2 oplus (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4) x_2$ Раскроем скобку по алгебраическим правилам: $f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_2 oplus x_1 x_2 x_2 neg x_3 x_4 oplus neg x_1 x_2 neg x_4$ Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ: $f(x_1,x_2,x_3,x_4) = neg x_1 neg x_4 oplus x_2 oplus neg x_1 x_2 neg x_4$ Заменим отрицание на прибавление $1$: $f(x_1,x_2,x_3,x_4) = (x_1 oplus 1) (x_4 oplus 1) oplus x_2 oplus (x_1 oplus 1) x_2 (x_4 oplus 1)$ $f(x_1,x_2,x_3,x_4) = x_1 x_4 oplus x_1 oplus x_4 oplus 1 oplus x_2 oplus x_1 x_2 x_4 oplus x_1 x_2 oplus x_2 x_4 oplus x_2$ Выкинем парные слагаемые и получим окончательную формулу: $f(x_1,x_2,x_3,x_4) = x_1 x_2 x_4 oplus x_1 x_2 oplus x_1 x_4 oplus x_2 x_4 oplus x_1 oplus x_4 oplus 1$ Метод треугольника Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами: Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от $000dots00$ до $111dots11$. Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности. Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже. Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности. Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке $111$ соответствует член $ABC$, ячейке $101$ — член $AC$, ячейке $010$ — член $B$, ячейке $000$ — член $1$ и т.д. Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина. Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций. Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных $P(A,B,C)$ показан на рисунке. Чтобы получить формулу, по которой рассчитывается какой-либо коэффициент, нужно из клетки, в которой он записан, пройтись всеми возможными путями влево, до столбца $»P»$ таблицы истинности, делая ходы влево и влево-вниз, записать значения в конечных ячейках и сложить их все между собой по модулю 2. Таким образом, в первом столбце сверху записан коэффициент $ a_0 = P(0,0,0) $, во втором — $ a_1 = P(0,0,0) oplus P(0,0,1) $, в третьем — $ a_2 = P(0,0,0) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,1,0) = P(0,0,0) oplus P(0,1,0) $, $ a_3 = P(0,0,0) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,1) = \ = P(0,0,0) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,1), $ и так далее, то есть при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически. Преобразование Мёбиуса Пусть задана булева функция $f: B^n rightarrow B, ;; B= $. Любая булева функция представима в виде полинома Жегалкина, притом единственным образом. Пусть $ i = (i_1, i_2, .. i_n), ;; i_k in $, и введем обозначение $ x ^ sim left[begin x,;; i_k=1 1, ;; i_k=0end right. $ Тогда полином Жегалкина можно записать как: $ f(x) = bigopluslimits_i alpha_i cdot x_1^ cdot x_2^ cdot$$dots$$cdot x_n^ $, где $alpha_i in $. Множество коэффициентов $ $ можно рассматривать как функцию $alpha$, заданной на множестве индексов $ i = (i_1, i_2, dots i_n)$, то есть $alpha: i mapsto alpha_i$. Очевидно, функцию $ f $ можно записать и следующим образом: $ f(x) = bigoplus limits_i alpha_i cdot [x_1 , ; $ если $ ;; i_1] cdot [x_2 , ; $ если $ ;; i_2] cdot$$dots$$cdot [x_n , ; $ если $ ;; i_n]$. Тут запись $[x_k , ; $ если $ ; i_k]$ означает, что элелемент $ x_k $ присутствует в соответствующем члене полинома только если $ i_k = 1 $. Тогда если для какого-то $x$, $i succ x$* ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. Отсюда ясно, что $ f(x) = bigoplus limits_ alpha_i $ $ (2) $ Найдем отображение $ f mapsto alpha$ . $*$ $i succ x$ обозначает, что $x$ «меньше» $i$ как последовательность бит Теорема: Пусть задана функция $ f $. Тогда функцию $ alpha_x $ можно найти по формуле: $alpha_x = bigoplus limits_ f(j)$ (3) Докажем при помощи индукции по количеству единиц в векторе $ x $ и для удобства обозначим это количество единиц $ wt(x) $. 1) База: если $ x = 0 $, то, очевидно $ f(0) = alpha_0 $ 2) Пускай теорема справедлива для всех сумм $wt(x) Огравление $Rightarrow $ Что нам стоит полином Жегалкина построить… Думаю, каждый, кто изучал или изучает в университете дискретную математику, знаком с понятием многочлена Жегалкина. Главная особенность этих многочленов состоит в том, что любую булеву функцию можно представить полиномом Жегалкина, причем единственным образом. Чаще всего для построения полиномов Жегалкина студентам предлагаются два метода построения таких полиномов: метод неопределенных коэффициентов и метод эквивалентных преобразований. Расчеты с использованием данных методов часто оказываются громоздкими. По невнимательности допустить ошибку не составляет труда. Под катом приведен один удобный алгоритм, для построения полиномов Жегалкина, который студенты воспринимают «на ура», т.к. требует только выполнение «механических действий» без применения каких-либо умственных усилий. Краткое описание метода можно найти в Википедии, но на мой взгляд по нему не совсем понятно, как быстро проводить вычисления. Мне метод известен под названием «метод треугольника Паскаля». Порядок проведения вычислений проще показать на примере. Далее я буду по шагам показывать, как должен выглядеть расчет на бумаге (или как его удобно проводить). Метод треугольника Паскаля Требуется построить полином Жегалкина для функции f. Для примера, в качестве функции f возьмем функцию голосования . Шаг 1. Строим таблицу значений функции (строки в таблице идут в порядке возрастания двоичных кодов). Таблицу лучше разместить в левой части листа. Шаг 2. Построение треугольника. Для этого берем вектор значения функции и выписываем его напротив первой строки таблицы: Далее заполняем треугольник, складывая попарно соседние значения по модулю 2, результат сложения выписываем ниже. Продолжаем вычисления, пока в строке не останется лишь одна цифра. Шаг 3. Построение полинома Жегалкина. Нас интересует левая сторона треугольника (значения выделены жирным): Числа на левой стороне (выделены жирным шрифтом) треугольника есть коэффициенты полинома при монотонных конъюнкциях, соответствующих наборам значений переменных. Теперь выпишем для наглядности эти конъюнкции. Конъюнкции выписываем по двоичным наборам в левой части таблицы по следующему принципу: если напротив переменной xi стоит 1, то переменная входит в конъюнкцию; в противном случае переменная отсутствует в конъюнкции. Набору (0,0,0) соответствует константа 1. Если принцип получения конъюнкций понятен, то столбец с ними можно (даже лучше) не выписывать, а сразу переходить к построению полинома. Для построения полинома нужны только конъюнкции из строк с единицами на левой стороне треугольника. Это и есть конъюнкции, входящие в состав полинома Жегалкина. Осталось лишь выписать сам полином: Если переменных в функции не 3, а 4 или больше, то метод работает без изменений, только увеличатся размеры таблиц. Тем не менее, в отличие от метода неопределенных коэффициентов, расчеты можно без особых усилий выполнить на листе бумаги. Полином Жегалкина Содержание: Функциональная замкнутость Функционально полные системы функций Полином Жегалкина Канонический полином Жегалкина Заменив в и используя распределительный закон для конъюнкции относительно сложения по модулю два, имеем Тогда, учитывая, что булеву функцию f можно представить в виде причем Такое представление булевой функции называется каноническим полиномом Жегалкина. По этой ссылке вы найдёте полный курс лекций по теории вероятности: Например, представим в виде полинома Жегалкина булеву функцию, заданную таблично (табл. 4.36). Найдем ее СДНФ и преобразуем: Как видим, , остальные полиномиальные коэффициенты равны 1. Нули можно не выписывать, а отсутствие слагаемого (конъюнкции) вида будет означать, что Таким образом, предпоследнее выражение тоже является полиномом Жегалкина. Итак, с помощью конъюкции и М2 любую логическую функцию можно единственным образом представить в виде многочлена. Иногда можно представить функцию в виде полинома Жегалкина более простым способом. Например, функцию будем рыскать в виде многочлена с неопределенными коэффициентами: При с, откуда Наконец, при Возможно вам будут полезны данные страницы: Функциональная замкнутость Обозначим через множество всех функций алгебры логики. Класс функций называется функционально замкнутым, если любая суперпозиция функций этого класса R принадлежит этому же классу. Это означает, что вместе с каждой функцией классу R принадлежит и функция , где — необязательно различные функции или аргументы и , если для всех = 1, 2, . либо либо Рассмотрим наиболее важные функционально замкнутые классы функций алгебры логики. Класс функций, сохраняющих константу 0 (). Так называют функции, для которых выполняется . Итак, . В строчной записи функции через ее значения они начинаются на 0, например Покажем, что . Действительно, Для п аргументов имеется функций от п аргументов, сохраняющих константу, поскольку на одном из двоичных наборов, а именно на х = (0. 0), значение/фиксировано, и для функции с п аргументами возможно подобрать лишь произвольных наборов аргументов. Такой класс функционально замкнут по определению, поскольку если Класс функций, сохраняющих константу 1 (). Так называют функции, для которых выполняется . Итак, В строчной записи функции, сохраняющие константу 1, оканчиваются на 1, например Покажем, что сохраняет 1. Это можно проверить подстановкой: Для К1 справедливо все то же, что и для K0. Класс самодвойственных функций (). Функция , удовлетворяющая условию называется двойственной по отношению к функции . Очевидно, что Таким образом, если т.е. множество булевых функций разбивается на пары взаимно-двойственных функций. Обратим внимание на свойства важнейших функций Подобная двойственность лежит в основе построения противоположных высказываний. Функция называется самодвойственной, если . Например, самодвойственна функция Самодвойственная функция полностью определяется своими значениями на половине наборов аргументов, поэтому число таких функций при п аргументах равно Множество самодвойственных функций образует функционально замкнутый класс. Пусть Обозначим_противоположный элемент на булевом кубе через . Тогда откуда следует, что любая композиция самодвойственных фун: ций не выходит из этого класса. Класс линейных функций (Ал). Функцию алгебры логики вида, называют линейной, если ее канонический полигон Жегалкина имеет вид многочлена первой степени: аналогичного обычному алгебра! ческому многочлену первой степени, но с коэффициентами кх виде 0 или 1. Число таких линейных функций от п аргументе равно , при их восемь из шестнадцати. Они образуй функционально замкнутый класс. В гл. 1 было доказано это утверх дение для непрерывных линейных отображений одного переме! ного. Можно доказать, что оно справедливо и для композици булевых линейных функций Для это1 в многочлен нужг подставить многочлены затем, используя переместительный и сочетательный законы дг операции суммы по модулю два, привести подобные слагаемы Тогда при каждом аргументе будет коэффициег который нужно просто вычислить. Класс монотонных функций (). В гл. 1 были определены пою тия порядок и упорядоченное множество. Для бесконечных множест это означает возможность введения бинарного отношения не более чем счетных — возможность перенумерования элементе и тем самым также введения . При этом эталоном сравнения служат натуральные числа. На множестве В введем полный порядок: по аналогии с отношением на множестве целых чисел Z. На мне жестве введем частичный порядок, означающий, что неравен ство выполняется тогда и тольк тогда, когда Например, 001100 00110 Два элемента называются сравнимыми между собог если . Частичным такой порядок является потом? что не все элементы сравнимы. Например, кортежи 1100 и 011 не сравнимы с помощью Поэтому не стоит путать частичны порядок на и полное упорядочивание, использовавшееся для табличного и строчного задания булевой функции (назове: его здесь). Очевидно, что если Функция называется монотонной, если для любы двух элементов , сравнимых между собой, из следует, что Монотонными будут не является монотон ной. Монотонные функции также образуют функционально замк нутый класс. Действительно, пусть Тогда композиция будет иметь вид , где Пусть . Тогда и ( а поскольку g — монотонна, то . Подставляя сюда явные выражения для , получим т.е. монотонную функцию. Следует отметить свойство монотонных булевых функций одно го и двух аргументов. Поскольку на сравнимы лишь и соответственно, а значения получаются , то такие монотонные функции будут сохраняющими 0 и 1, т.е. пересече нием этих двух подклассов. Каждый из пяти рассмотренных классов функций обладает очен] важным свойством: любая из функций алгебры логики, полученная Функционально полные системы функций Систему 5 функций алгебры логики называю функционально полной, если любую функцию алгебры логик можно записать с помощью суперпозиции некоторого набора бу левых функций Очевидно, что если S — функционально полная система, то добавление любого числа булевых функций не изменит статус системы как функционально полной. Функционально полная система функций называется базисо! в пространстве , если удаление хотя бы одной из функций входящих в нее, превращает эту систему в функционально не полную. Ранее было доказано, что через функции , можно выразить любые функции алгебры логики, приведя их виду СКИФ или СДНФ. Следовательно, система этих трех функ ций полна. Так же мы представляли любую функцию в виде ком позиции суммы по модулю два, конъюнкции и константы 1 (удаление всех 0 приводило к равной функции). Однако это не един ственные возможности для представления функций алгебры логику Оказывается, существует довольно много функционально полны систем. _Например, булевы функции можно выразить только через и воспользовавшись правилом Де Моргана и представив one рацию конъюнкции через дизъюнкцию и отрицание, так ка Критерий функциональной полноты системы функций сфор мулирован в теореме Поста—Яблонского. Для того чтобы система S функций алгебры логики был функционально полной, необходимо и достаточно, чтобы она содер жала функцию: не сохраняющую константу 0; не сохраняющую константу 1; не являющуюся самодвойственной; не являющуюся линейной; не являющуюся монотонной. Выбор элементарных функций для базиса можно осуществлять с помощью табл. 4.37, где плюсом отмечены свойства, которыми эти функции обладают. В ней приведено распределение различных булевых функций двух переменных по пяти рассмотренным функционально замкнутым классам. Какое минимальное число булевых функций должен содержать базис? Просим не путать обозначения функций в этой таблице, например с аналогичной нумерацией в подразд. 4.2. Из табл. 4.37 видно, что каждая из функций — стрелка Пирса и — штрих Шеффера является минимальным базисом, так как соответствует условиям теоремы Поста—Яблонского. Это подтверждает и возможность выражать эти функции через отрицание, конъюнкцию и дизъюнкцию по формулам: Таким образом, для описания булевой алгебры достаточно одной функции. Другое дело, что стрелку Пирса и штрих Шеффера трудно интерпретировать в теории множеств и реализовать в виде элементарных логических схем через элементы И — НЕ и ИЛИ НЕ, а формулы и логические схемы, составленные только из них, являются громоздкими. Вообще говоря, в алгебре логики доказано, что минимальный базис содержит не более четырех функций. Хотя существует базис, который содержит ровно четыре функции и образует функционально полную систему: Приведем примеры основных функционально полных систем булевых функций: и, или, не, которые лежат в основе алгебры высказываний или булевой алгебры, Заметим, что полная система функций будет избыточной. Действительно, удалив из него одну из функций или и выразив их с помощью законов Де Моргана через или соответственно, можно получить новую функционально полную систему с базисом соответственно. Рассматриваемая проблема представления логических функций заключается не только в выборе минимального базиса, но и в выборе формы наиболее экономичного представления этих функций. Так, совершенные дизъюнктивные и конъюнктивные нормальные формы (СДНФ и СКНФ) менее экономичны, чем некоторые из ДНФ и КНФ, хотя и обладают определенными достоинствами, например дают однозначное представление логической функции. Поэтому одинаково важны обе встречные проблемы: с одной стороны, минимизация булевых функций, т.е. приведение к наиболее экономичному виду, и с другой стороны — придание им совершенного вида, важного в некоторых приложениях, например для получения выводов. Уточним, что минимальной называется такая форма представления логических функций, которая содержит минимальное количество термов и переменных в термах, а значит, минимальная форма предполагает завершение процесса упрощения. Можно построить различные формальные системы — алгебры — в зависимости от выбранных в качестве базисных логических операций. Так, булевы функции вида образуют булеву алгебру, а операции дизъюнкции, конъюнкции и отрицания образуют базис булевой алгебры. Множество булевых функций в базисе образуют алгебру Жегалкина, а операции и 1 образуют базис Жегалкина. Достоинством алгебры Жегалкина является арифметизация логики, благодаря чему двузначная аристотелева логика нашла свое практическое применение. Поскольку в ней справедлив закон исключенного третьего, то алгебра Жегалкина обладает одной существенной особенностью: она непротиворечива, так как непротиворечива ее система аксиом. Анализ построения различных алгебр с помощью выбора соответствующего языка дает возможность увидеть принципы построения любой науки вообще. Выбирая, например, язык будущей системы, примем во внимание структуру любой науки, будь то алгебра, геометрия, математическая логика или языки программирования. Лекции: Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
- Построение полинома Жегалкина
- По таблице истинности
- Преобразование дизъюнктивной нормальной формы
- Метод треугольника
- Преобразование Мёбиуса
- Что нам стоит полином Жегалкина построить…
- Метод треугольника Паскаля
- Полином Жегалкина
- Функциональная замкнутость
- Функционально полные системы функций
- 📺 Видео
Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
- Услуги проектирования
- Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв]
- Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Видео:Многочлен полином Жегалкина Метод неопределенных коэффициентов Метод треугольника ПаскаляСкачать

Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Полином Жегалкина — многочлен над кольцом $mathbb _2$, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения — исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой .
Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина.
Полином Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также константы
Формально полином Жегалкина можно представить в виде
или в более формализованном виде как:
$P = a oplus bigoplus_ < begin 1leq i_1 Примеры полиномов Жегалкина:
- $ P = B oplus AB;$
- $ P = X oplus YZ oplus ABX oplus ABDYZ;$
- $ P = 1 oplus A oplus ABD.$
Видео:A.2.19 Полином ЖегалкинаСкачать

Полнота
По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали
- Хотя бы одна функция, не сохраняющая $0$;
- Хотя бы одна функция, не сохраняющая $1$;
- Хотя бы одна нелинейная функция;
- Хотя бы одна немонотонная функция;
- Хотя бы одна несамодвойственная функция.
Исходя из этого, система функций $bigllangle wedge, oplus, 1 bigrrangle$ является полной:
| $x_0$ | $x_1$ | $dots$ | $x_n$ | $1$ | $land$ | $oplus$ |
| $0$ | $0$ | $dots$ | $0$ | $1$ | $0$ | $0$ |
| $1$ | $0$ | $dots$ | $0$ | $1$ | $0$ | $1$ |
| $vdots$ | $vdots$ | $vdots$ | $vdots$ | $vdots$ | $vdots$ | $vdots$ |
| $1$ | $1$ | $dots$ | $1$ | $1$ | $1$ | $0$ |
| . | . | . | сохраняет 0 | $0$ | $1$ | $1$ |
| . | . | . | сохраняет 1 | $1$ | $1$ | $0$ |
| . | . | . | самодвойственная | $0$ | $0$ | $0$ |
| . | . | . | монотонная | $1$ | $1$ | $0$ |
| . | . | . | линейная | $1$ | $0$ | $1$ |
На основе этой системы и строятся полиномы Жегалкина.
Видео:Полином ЖегалкинаСкачать

Существование и единственность представления
Теорема Жегалкина: Каждая булева функция единственным образом представляется в виде полинома Жегалкина.
Заметим, что различных булевых функций от $n$ переменных $2^ $ штук. При этом конъюнкций вида $x_ ldots x_ $ существует ровно $2^n$, так как из $n$ возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит $0$ или $1$, то есть существует $2^ $ различных полиномов Жегалкина от $n$ переменных.
Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него . Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.
Видео:Представление в виде Полинома Жегалкина функции заданной в виде СДНФСкачать
Построение полинома Жегалкина
Существует несколько способов построения полинома Жегалкина.
По таблице истинности
Пусть для функции $f(x_1,x_2,dots,x_n)$ задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что $ a oplus 1 = bar $, а $ a oplus 0 = a$. За каждую подстановку находим только один коэффициент.
Пример: Дана функция $f(x_1,x_2,x_3,x_4)$ и её таблица истинности:
| $x_1$ | $x_2$ | $x_3$ | $x_4$ | $f(x_1,x_2,x_3,x_4)$ |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Построим для неё полином Жегалкина:
$f(x_1,x_2,x_3,x_4) = a_ oplus a_ x_1 oplus a_ x_2 oplus a_ x_3 oplus a_ x_4 oplus a_ x_1 x_2 oplus a_ x_1 x_3 oplus a_ x_1 x_4 oplus \ oplus a_ x_2 x_3 oplus a_ x_2 x_4 oplus a_ x_3 x_4 oplus a_ x_1 x_2 x_3 oplus a_ x_1 x_2 x_4 oplus \ oplus a_ x_1 x_3 x_4 oplus a_ x_2 x_3 x_4 oplus a_ x_1 x_2 x_3 x_4$
Так как $f(0,0,0,0) = 0$, то $a_ = 0$.
Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:
$f(1,0,0,0) = a_ oplus a_ = 1 Rightarrow a_ = 1$
$f(0,1,0,0) = a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(0,0,1,0) = a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(0,0,0,1) = a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(1,1,0,0) = a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$
$f(1,0,1,0) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$
$f(1,0,0,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$
$f(0,1,1,0) = a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 1$
$f(0,1,0,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(0,0,1,1) = a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(1,1,1,0) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$
$f(1,1,0,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 0$
$f(1,0,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 1 Rightarrow a_ = 0$
$f(0,1,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$
$f(1,1,1,1) = a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ oplus \ oplus a_ oplus a_ oplus a_ oplus a_ oplus a_ = 0 Rightarrow a_ = 1$
Таким образом, полином Жегалкина выглядит так:
$f(x_1,x_2,x_3,x_4) = x_1 oplus x_1 x_3 oplus x_1 x_4 oplus x_2 x_3 oplus x_2 x_3 x_4 oplus x_1 x_2 x_3 x_4$
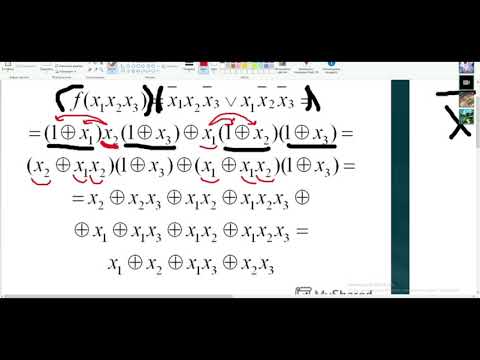
Преобразование дизъюнктивной нормальной формы
Этот способ основан на том, что $ X oplus 1 = bar $. Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило Де-Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю , а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу: $ A lor B = AB oplus A oplus B $ $ (1) $.
Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ.
Пример: Дана функция в ДНФ $ f(x_1,x_2,x_3,x_4) = (x_1 land x_2 land neg x_3 land x_4) lor (neg x_1 land neg x_4) lor (x_1 land x_2) lor x_2 $, построим полином Жегалкина.
Запишем функцию так:
$f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 + neg x_1 neg x_4 + x_1 x_2 + x_2$;
Сгруппируем слагаемые и воспользуемся преобразованием (1):
$f(x_1,x_2,x_3,x_4) = (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_1 x_2 neg x_3 x_4 neg x_1 neg x_4) + (x_1 x_2 oplus x_2 oplus oplus x_1 x_2 x_2)$
Воспользуемся свойствами конъюнкции $A land A = A$ и $neg A land A = 0$, а также тем, что $A oplus A = 0$, и упростим выражение:
$f(x_1,x_2,x_3,x_4) = (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4) + x_2$
Ещё раз воспользуемся преобразованием (1):
$f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_2 oplus (x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4) x_2$
Раскроем скобку по алгебраическим правилам:
$f(x_1,x_2,x_3,x_4) = x_1 x_2 neg x_3 x_4 oplus neg x_1 neg x_4 oplus x_2 oplus x_1 x_2 x_2 neg x_3 x_4 oplus neg x_1 x_2 neg x_4$
Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:
$f(x_1,x_2,x_3,x_4) = neg x_1 neg x_4 oplus x_2 oplus neg x_1 x_2 neg x_4$
Заменим отрицание на прибавление $1$:
$f(x_1,x_2,x_3,x_4) = (x_1 oplus 1) (x_4 oplus 1) oplus x_2 oplus (x_1 oplus 1) x_2 (x_4 oplus 1)$
$f(x_1,x_2,x_3,x_4) = x_1 x_4 oplus x_1 oplus x_4 oplus 1 oplus x_2 oplus x_1 x_2 x_4 oplus x_1 x_2 oplus x_2 x_4 oplus x_2$
Выкинем парные слагаемые и получим окончательную формулу:
$f(x_1,x_2,x_3,x_4) = x_1 x_2 x_4 oplus x_1 x_2 oplus x_1 x_4 oplus x_2 x_4 oplus x_1 oplus x_4 oplus 1$
Метод треугольника
Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:
- Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от $000dots00$ до $111dots11$.
- Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
- Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
- Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
- Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке $111$ соответствует член $ABC$, ячейке $101$ — член $AC$, ячейке $010$ — член $B$, ячейке $000$ — член $1$ и т.д.
- Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.
Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций.
Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных $P(A,B,C)$ показан на рисунке.
Чтобы получить формулу, по которой рассчитывается какой-либо коэффициент, нужно из клетки, в которой он записан, пройтись всеми возможными путями влево, до столбца $»P»$ таблицы истинности, делая ходы влево и влево-вниз, записать значения в конечных ячейках и сложить их все между собой по модулю 2.
Таким образом, в первом столбце сверху записан коэффициент $ a_0 = P(0,0,0) $,
во втором — $ a_1 = P(0,0,0) oplus P(0,0,1) $,
в третьем — $ a_2 = P(0,0,0) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,1,0) = P(0,0,0) oplus P(0,1,0) $,
$ a_3 = P(0,0,0) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,0,1) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,1) = \ = P(0,0,0) oplus P(0,1,0) oplus P(0,1,0) oplus P(0,1,1), $
и так далее, то есть при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически.
Преобразование Мёбиуса
Пусть задана булева функция $f: B^n rightarrow B, ;; B= $. Любая булева функция представима в виде полинома Жегалкина, притом единственным образом.
Пусть $ i = (i_1, i_2, .. i_n), ;; i_k in $, и введем обозначение $ x ^ sim left[begin x,;; i_k=1 1, ;; i_k=0end right. $
Тогда полином Жегалкина можно записать как: $ f(x) = bigopluslimits_i alpha_i cdot x_1^ cdot x_2^ cdot$$dots$$cdot x_n^ $, где $alpha_i in $.
Множество коэффициентов $ $ можно рассматривать как функцию $alpha$, заданной на множестве индексов $ i = (i_1, i_2, dots i_n)$, то есть $alpha: i mapsto alpha_i$.
Очевидно, функцию $ f $ можно записать и следующим образом: $ f(x) = bigoplus limits_i alpha_i cdot [x_1 , ; $ если $ ;; i_1] cdot [x_2 , ; $ если $ ;; i_2] cdot$$dots$$cdot [x_n , ; $ если $ ;; i_n]$.
Тут запись $[x_k , ; $ если $ ; i_k]$ означает, что элелемент $ x_k $ присутствует в соответствующем члене полинома только если $ i_k = 1 $. Тогда если для какого-то $x$, $i succ x$* ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет. Отсюда ясно, что $ f(x) = bigoplus limits_ alpha_i $ $ (2) $ Найдем отображение $ f mapsto alpha$ .
$*$ $i succ x$ обозначает, что $x$ «меньше» $i$ как последовательность бит
Теорема: Пусть задана функция $ f $. Тогда функцию $ alpha_x $ можно найти по формуле: $alpha_x = bigoplus limits_ f(j)$ (3)
Докажем при помощи индукции по количеству единиц в векторе $ x $ и для удобства обозначим это количество единиц $ wt(x) $.
1) База: если $ x = 0 $, то, очевидно $ f(0) = alpha_0 $
2) Пускай теорема справедлива для всех сумм $wt(x) Огравление $Rightarrow $
Видео:СДНФ СКНФ Полином Жегалкина для логических выраженийСкачать

Что нам стоит полином Жегалкина построить…
Думаю, каждый, кто изучал или изучает в университете дискретную математику, знаком с понятием многочлена Жегалкина.
Главная особенность этих многочленов состоит в том, что любую булеву функцию можно представить полиномом Жегалкина, причем единственным образом.
Чаще всего для построения полиномов Жегалкина студентам предлагаются два метода построения таких полиномов: метод неопределенных коэффициентов и метод эквивалентных преобразований.
Расчеты с использованием данных методов часто оказываются громоздкими. По невнимательности допустить ошибку не составляет труда.
Под катом приведен один удобный алгоритм, для построения полиномов Жегалкина, который студенты воспринимают «на ура», т.к. требует только выполнение «механических действий» без применения каких-либо умственных усилий. Краткое описание метода можно найти в Википедии, но на мой взгляд по нему не совсем понятно, как быстро проводить вычисления. Мне метод известен под названием «метод треугольника Паскаля».
Порядок проведения вычислений проще показать на примере. Далее я буду по шагам показывать, как должен выглядеть расчет на бумаге (или как его удобно проводить).
Видео:Многочлен полином Жегалкина Метод неопределенных коэффициентовСкачать

Метод треугольника Паскаля
Требуется построить полином Жегалкина для функции f. Для примера, в качестве функции f возьмем функцию голосования .
Шаг 1. Строим таблицу значений функции (строки в таблице идут в порядке возрастания двоичных кодов). Таблицу лучше разместить в левой части листа.
Шаг 2. Построение треугольника.
Для этого берем вектор значения функции и выписываем его напротив первой строки таблицы:
Далее заполняем треугольник, складывая попарно соседние значения по модулю 2, результат сложения выписываем ниже.
Продолжаем вычисления, пока в строке не останется лишь одна цифра.
Шаг 3. Построение полинома Жегалкина.
Нас интересует левая сторона треугольника (значения выделены жирным):
Числа на левой стороне (выделены жирным шрифтом) треугольника есть коэффициенты полинома при монотонных конъюнкциях, соответствующих наборам значений переменных.
Теперь выпишем для наглядности эти конъюнкции. Конъюнкции выписываем по двоичным наборам в левой части таблицы по следующему принципу: если напротив переменной xi стоит 1, то переменная входит в конъюнкцию; в противном случае переменная отсутствует в конъюнкции. Набору (0,0,0) соответствует константа 1.
Если принцип получения конъюнкций понятен, то столбец с ними можно (даже лучше) не выписывать, а сразу переходить к построению полинома.
Для построения полинома нужны только конъюнкции из строк с единицами на левой стороне треугольника.
Это и есть конъюнкции, входящие в состав полинома Жегалкина. Осталось лишь выписать сам полином:
Если переменных в функции не 3, а 4 или больше, то метод работает без изменений, только увеличатся размеры таблиц. Тем не менее, в отличие от метода неопределенных коэффициентов, расчеты можно без особых усилий выполнить на листе бумаги.
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Полином Жегалкина
Содержание:
- Функциональная замкнутость
- Функционально полные системы функций
| Полином Жегалкина |
Канонический полином Жегалкина
Заменив в 



Такое представление булевой функции называется каноническим полиномом Жегалкина.
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Например, представим в виде полинома Жегалкина булеву функцию, заданную таблично (табл. 4.36).
Найдем ее СДНФ и преобразуем:
Как видим, 

Таким образом, предпоследнее выражение тоже является полиномом Жегалкина.
Итак, с помощью конъюкции и М2 любую логическую функцию можно единственным образом представить в виде многочлена. Иногда можно представить функцию в виде полинома Жегалкина более простым способом. Например, функцию 

При 

Возможно вам будут полезны данные страницы:
Функциональная замкнутость
Обозначим через 
Класс функций 
Это означает, что вместе с каждой функцией 







Рассмотрим наиболее важные функционально замкнутые классы функций алгебры логики.
Класс функций, сохраняющих константу 0 (


Покажем, что
. Действительно,

Для п аргументов имеется 

Такой класс функционально замкнут по определению, поскольку если
Класс функций, сохраняющих константу 1 (



Покажем, что 
Для К1 справедливо все то же, что и для K0.
Класс самодвойственных функций (





Обратим внимание на свойства важнейших функций 

Функция 

Самодвойственная функция полностью определяется своими значениями на половине наборов аргументов, поэтому число таких функций при п аргументах равно
Множество самодвойственных функций образует функционально замкнутый класс.
Пусть 


Класс линейных функций (Ал). Функцию алгебры логики вида, 
Жегалкина имеет вид многочлена первой степени: 








Класс монотонных функций (


На множестве В введем полный порядок: 





Два элемента 





Функция 


Монотонными будут 
Монотонные функции также образуют функционально замк нутый класс. Действительно, пусть 









Следует отметить свойство монотонных булевых функций одно го и двух аргументов. Поскольку на 



Каждый из пяти рассмотренных классов функций обладает очен] важным свойством: любая из функций алгебры логики, полученная
Функционально полные системы функций
Систему 5 функций 
Очевидно, что если S — функционально полная система, то добавление любого числа булевых функций не изменит статус системы как функционально полной.
Функционально полная система функций называется базисо! в пространстве 
Ранее было доказано, что через функции 
_Например, булевы функции можно выразить только через 

Критерий функциональной полноты системы функций сфор мулирован в теореме Поста—Яблонского.
Для того чтобы система S функций 
- не сохраняющую константу 0;
- не сохраняющую константу 1;
- не являющуюся самодвойственной;
- не являющуюся линейной; не являющуюся монотонной.
Выбор элементарных функций для базиса можно осуществлять с помощью табл. 4.37, где плюсом отмечены свойства, которыми эти функции обладают. В ней приведено распределение различных булевых функций двух переменных по пяти рассмотренным функционально замкнутым классам.
Какое минимальное число булевых функций должен содержать базис?
Просим не путать обозначения функций в этой таблице, например 
Из табл. 4.37 видно, что каждая из функций 


Вообще говоря, в алгебре логики доказано, что минимальный базис содержит не более четырех функций. Хотя существует базис, который содержит ровно четыре функции и образует функционально полную систему:
Приведем примеры основных функционально полных систем булевых функций:
и, или, не, которые лежат в основе алгебры высказываний или булевой алгебры,
Заметим, что полная система функций 





Рассматриваемая проблема представления логических функций заключается не только в выборе минимального базиса, но и в выборе формы наиболее экономичного представления этих функций.
Так, совершенные дизъюнктивные и конъюнктивные нормальные формы (СДНФ и СКНФ) менее экономичны, чем некоторые из ДНФ и КНФ, хотя и обладают определенными достоинствами, например дают однозначное представление логической функции. Поэтому одинаково важны обе встречные проблемы: с одной стороны, минимизация булевых функций, т.е. приведение к наиболее экономичному виду, и с другой стороны — придание им совершенного вида, важного в некоторых приложениях, например для получения выводов.
Уточним, что минимальной называется такая форма представления логических функций, которая содержит минимальное количество термов и переменных в термах, а значит, минимальная форма предполагает завершение процесса упрощения.
Можно построить различные формальные системы — алгебры — в зависимости от выбранных в качестве базисных логических операций.
Так, булевы функции вида 
Множество булевых функций в базисе 

Анализ построения различных алгебр с помощью выбора соответствующего языка дает возможность увидеть принципы построения любой науки вообще.
Выбирая, например, язык будущей системы, примем во внимание структуру любой науки, будь то алгебра, геометрия, математическая логика или языки программирования.
Лекции:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
📺 Видео
Полином ЖегалкинаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Полиномы Жегалкина. Замыкание и замкнутые классы. 3 лекцияСкачать

20-2 Полиномы ЖегалкинаСкачать

Лекция 2. Полином Жегалкина (теоретическая часть)Скачать

Многочлен полином Жегалкина Метод треугольника Паскаля Преобразование формулСкачать

A.2.15 Построение совершенных дизъюнктивной и конъюнктивной нормальных форм (СДНФ и СКНФ)Скачать

ДНФ. Импликанты. Полиномы Жегалкина. 2 семинарСкачать

Полиномы ЖегалкинаСкачать

Алгебра ЖегалкинаСкачать

Многочлен Жегалкина.Скачать

ПолиномСкачать

ДМ 1 курс - 4 лекция - преобразование Мёбиуса, схемы из функциональных элементовСкачать












 . Действительно,
. Действительно, 


















