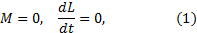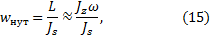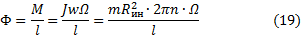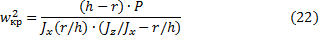Вектор кинетического момента гироскопа (6 видео)

Лекция 11. Гироскопы.

В данной лекции рассматриваются следующие вопросы:

1. Гироскопы. Свободный гироскоп.

2. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации.

3. Гироскопические силы, их природа и проявление.

4. Волчки. Устойчивость вращения симметричного волчка.

Изучение данных вопросов необходимо в дисциплине «Детали машин».

Содержание

Гироскопы. Свободный гироскоп.
Прецессия гироскопа под действием внешних сил. Элементарная теория.
Прецессия гироскопа пол действием внешних сил. Отход от элементарной теории. Нутации.
Гироскопические силы.
Волчки.
ГИРОСКО́П
гироскоп
💥 Видео

Гироскопы. Свободный гироскоп.

Гироскоп — это массивное аксиально-симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии.

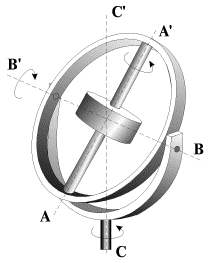
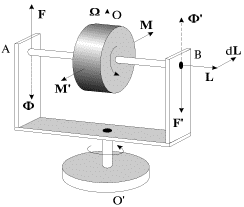
В этом случае моменты всех внешних сил, включая и силу тяжести, относительно центра масс гироскопа равны нулю. Это можно реализовать, например, поместив гироскоп в карданов подвес, изображенный на рис.1.

M =0, dL dt =0, (1)

и момент импульса сохраняется:

Гироскоп ведет себя так же, как и свободнее тело вращения. В зависимости от начальных условий возможны два варианта поведения гироскопа:

1. Если гироскоп раскручен вокруг оси симметрии, то направления момента импульса и угловой скорости совпадают:

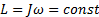
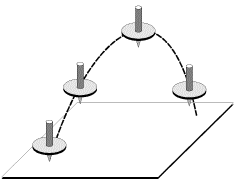
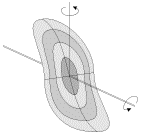
L = Jω = const , (3)

и направление оси симметрии гироскопа остается неизменным. В этом можно убедиться, поворачивая подставку, на которой расположен карданов подвес — при произвольных поворотах подставки ось гироскопа сохраняет неизменное направление в пространстве. По этой же причине волчок, «запущенный» на листе картона и подброшенный вверх (рис.2), сохраняет направление своей оси во время полета, и, падая острием на картон, продолжает устойчиво вращаться, пока не израсходуется запас его кинетической энергии.

Свободный гироскоп, раскрученный вокруг оси симметрии, обладает весьма значительной устойчивостью. Из основного уравнения моментов следует, что изменение момента импульса

∆ L = 0 ∆ t Mdt (4)

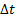
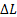
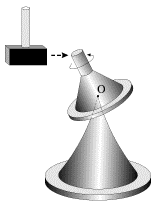
Если интервал времени ∆ t мал, то и ∆ L мало, то есть при кратковременных воздействиях даже очень больших сил движение гироскопа изменяется незначительно. Гироскоп как бы сопротивляется попыткам изменить его момент импульса и кажется «затвердевшим».

Возьмем гироскоп конусообразной формы, опирающийся на стержень подставки в своем центре масс О (рис. 3). Если тело гироскопа не вращается, то оно находится в состоянии безразличного равновесия, и малейший толчок сдвигает его с места. Если же это тело привести в быстрое вращение вокруг своей оси, то даже сильные удары деревянным молотком не смогут сколько-нибудь значительно изменить направление оси гироскопа в пространстве. Устойчивость свободного гироскопа используется в различных технических устройствах, например, в автопилоте.

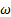
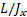
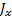
2. Если свободный гироскоп раскручен так, что вектор мгновенной угловой скорости и ось симметрии гироскопа не совпадают (как правило, это несовпадение при быстром вращении бывает незначительным), то наблюдается движение, описанное как «свободная регулярная прецессия». Применительно же к гироскопу его называют нутацией. При этом ось симметрии гироскопа, векторы L и ω лежат в одной плоскости, которая вращается вокруг направления L = const с угловой скоростью, равной L / J x где J x — момент инерции гироскопа относительно главной центральной оси, перпендикулярной оси симметрии. Эта угловая скорость (назовем ее скоростью нутации) при быстром собственном вращении гироскопа оказывается достаточно большой, и нутация воспринимается глазом как мелкое дрожание оси симметрии гироскопа.

Нутационное движение легко продемонстрировать с помощью гироскопа, показанного на рис. 3 — оно возникает при ударах молотком по стержню вращающегося вокруг своей оси гироскопа. При этом чем сильнее раскручен гироскоп, тем больше его момент импульса L — тем больше скорость нутации и тем «мельче» дрожания оси фигуры. Этот опыт демонстрирует еще одну характерную особенность нутации — с течением времени она постепенно уменьшается и исчезает. Это — следствие неизбежного трения в опоре гироскопа.

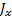
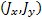
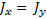
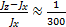
Наша Земля — своего рода гироскоп, и ей тоже свойственно нутационное движение. Это связано с тем, что Земля несколько приплюснута с полюсов, в силу чего моменты инерции относительно оси симметрии J x и относительно оси, лежащей в экваториальной плоскости ( J x , J y ) различаются. При этом J x = J y , а J z — J x J x ≈ 1 300 . В системе отсчета, связанной с Землей, ось вращения движется по поверхности конуса вокруг оси симметрии Земли с угловой скоростью w₀, то есть она совершает один оборот примерно за 300 дней. На самом деле в силу, как предполагается, неабсолютной жесткости Земли, это время оказывается больше — оно составляет около 440 суток. При этом расстояние точки земной поверхности, через которую проходит ось вращении, от точки, через которую проходит ось симметрии (Северный полюс), равно всего нескольким метрам. Нутационное движение Земли не затухает — по-видимому, его поддерживают сезонные изменения, происходящие на поверхности

Прецессия гироскопа под действием внешних сил. Элементарная теория.

Рассмотрим теперь ситуацию, когда к оси гироскопа приложена сила, линия действия которой не проходит через точку закрепления. Опыты показывают, что в этом случае гироскоп ведет себя весьма необычным образом.

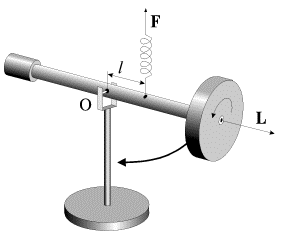
Если к оси шарнирно закрепленного в точке О гироскопа (рис. 4) прикрепить пружину и тянуть за нее вверх с силой F , то ось гироскопа будет перемещаться не в направлении силы, а перпендикулярно к ней, вбок. Это движение называется прецессией гироскопа под действием внешней силы.

Опытным путем можно установить, что угловая скорость прецессии зависит не только от величины силы F (рис.4), но и от того, к какой точке оси гироскопа эта сила приложена: с увеличением F и ее плеча l относительно точки закрепления О скорость прецессии увеличивается. При этом оказывается, что чем сильнее раскручен гироскоп, тем меньше угловая скорость прецессии при данных F и l .

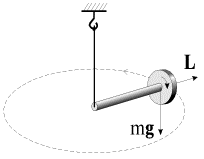
В качестве силы F , вызывающей прецессию, может выступать сила тяжести, если точка закрепления гироскопа не совпадает с центром масс. Так, если стержень с быстро вращающимся диском подвесить на нитке (рис. 5), то он не опускается вниз, как это можно было бы предположить, а совершает прецессионное движение вокруг нитки. Наблюдение прецессии гироскопа под действием силы тяжести в некотором смысле даже удобнее — линия действия силы «автоматически» смещается вместе с осью гироскопа, сохраняя свою ориентацию в пространстве.

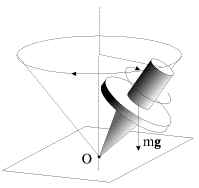
Можно привести и другие примеры прецессии — например, движение оси хорошо известной детской игрушки — юлы с заостренным концом (рис.6). Юла, раскрученная вокруг своей оси и поставленная на горизонтальную плоскость слегка наклонно, начинает прецессировать вокруг вертикальной оси под действием силы тяжести (рис.6).

Точное решение задачи о движении гироскопа в поле внешних сил довольно выражение для угловой скорости прецессии можно легко получить в рамках так называемой элементарной теории гироскопа. В этой теории делается допущение, что мгновенная угловая скорость вращения гироскопа и его момент импульса направлены вдоль оси симметрии гироскопа. Другими словами, предполагается, что угловая скорость вращения гироскопа вокруг своей оси значительно больше угловой скорости прецессии:

ω ≫ Ω 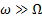(5)

так что вкладом в L , обусловленным прецессионным движением гироскопа, можно пренебречь. В этом приближении момент импульса гироскопа, очевидно, равен

L = J z ω 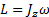(6)

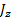
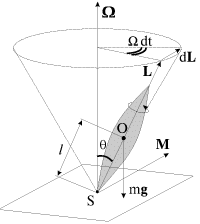
где J z — момент инерции относительно оси симметрии.

Итак, рассмотрим тяжелый симметричный гироскоп, у которого неподвижная точка S (точка опоры о подставку) не совпадает с центром масс О (рис. 7).

Момент силы тяжести относительно точки S

M = mglsunθ 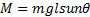(7)

где θ — угол между вертикалью и осью симметрии гироскопа. Вектор M направлен по нормали к плоскости, в которой лежат ось симметрии гироскопа и вертикаль, проведенная через точку S (рис. 7). Сила реакции опоры проходит через S, и ее момент относительно этой точки равен нулю.

Изменение момента импульса L определяется выражением

При этом и L , и ось волчка прецессируют вокруг вертикального направления с угловой скоростью Ω . Еще раз подчеркнем: делается допущение, что выполнено условие (5) и что L постоянно направлен вдоль оси симметрии гироскопа. Из рис.95 следует, что

dL = Lsinθ Ω dt 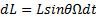(9)

В векторном виде

dL = Ω × Ldt 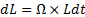(10)

Сравнивая (8) и (10), получаем следующую связь между моментом силы M , моментом импульса L и угловой скоростью прецессии Ω :

M = Ω × L 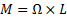(11)

Это соотношение позволяет определить направление прецессии при заданном направлении вращения волчка вокруг своей оси.

Обратим внимание, что M определяет угловую скорость прецессии, а не угловое ускорение, поэтому мгновенное «выключение» M приводит к мгновенному же исчезновению прецессии, то есть прецессионное движение является безынерционным.

Сила, вызывающая прецессионное движение, может иметь любую природу. Для поддержания этого движения важно, чтобы вектор момента силы M поворачивался вместе с осью гироскопа. Как уже было отмечено, в случае силы тяжести это достигается автоматически. При этом из (11) (см. также рис. 7) можно получить:

mglsinθ = Ω J z ωsinθ 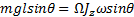(12)

Если учесть, что в нашем приближении справедливо соотношение (6), то для угловой скорости прецессии получим

Ω = mgl J z ω (13)

Следует отметить, что Ω не зависит от угла θ наклона оси гироскопа и обратно пропорциональна w, что хорошо согласуется с опытными данными.

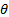
Прецессия гироскопа пол действием внешних сил. Отход от элементарной теории. Нутации.

Опыт показывает, что прецессионное движение гироскопа под действием внешних сил в общем случае сложнее, чем то, которое было описано выше в рамках элементарной теории. Если сообщить гироскопу толчок, изменяющий угол θ 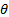(см. рис.7), то прецессия перестанет быть равномерной (часто говорят: регулярной), а будет сопровождаться мелкими вращениями и дрожаниями вершины гироскопа — нутациями. Для их описания необходимо учесть несовпадение вектора полного момента импульса L , мгновенной угловой скорости вращения w и оси симметрии гироскопа.

Точная теория гироскопа выходит за рамки курса общей физики. Из соотношения dL = Mdt следует, что конец вектора L движется в направлении M , то есть перпендикулярно к вертикали и к оси гироскопа. Это значит, что проекции вектора L на вертикаль L_B и на ось гироскопа L ₀ остаются постоянными. Еще одной постоянной является энергия

E = T + mg l cosθ 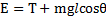(14)

где T — кинетическая энергия гироскопа. Выражая L_B , L ₀ и T через углы Эйлера и их производные, можно, с помощью уравнений Эйлера, описать движение тела аналитически.

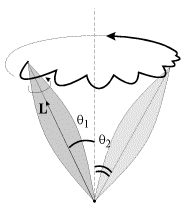
Результат такого описания оказывается следующим: вектор момента импульса L описывает неподвижный в пространстве конус прецессии, и при этом ось симметрии гироскопа движется вокруг вектора L по поверхности конуса нутаций. Вершина конуса нутаций, как и вершина конуса прецессии, находится в точке закрепления гироскопа, а ось конуса нутаций совпадает по направлению с L и движется вместе с ним. Угловая скорость нутаций определяется выражением

w нут = L J s ≈ J z ω J s , (15)

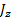
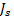
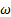
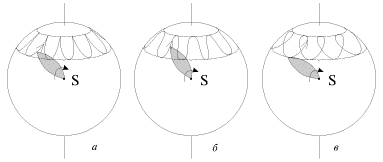
где J z и J s — моменты инерции тела гироскопа относительно оси симметрии и относительно оси, проходящей через точку опоры и перпендикулярной оси симметрии, ω — угловая скорость вращения вокруг оси симметрии.

Таким образом, ось гироскопа участвует в двух движениях: нутационном и прецессионном. Траектории абсолютного движения вершины гироскопа представляют собой замысловатые линии, примеры которых представлены на рис. 8.

Характер траектории, по которой движется вершина гироскопа, зависит от начальных условий. В случае рис. 8, а гироскоп был раскручен вокруг оси симметрии, установлен на подставке под некоторым углом к вертикали и осторожно отпущен. В случае рис. 8, б ему, кроме того, был сообщен некоторый толчок вперед, а в случае рис. 8, в — толчок назад по ходу прецессии. Кривые на рис. 8 вполне аналогичны циклоидам, описываемым точкой на ободе колеса, катящегося по плоскости без проскальзывания или с проскальзыванием в ту или иную сторону. И лишь сообщив гироскопу начальный толчок вполне определенной величины и направления, можно добиться того, что ось гироскопа будет прецессировать без нутаций. Чем быстрее вращается гироскоп, тем больше угловая скорость нутаций и тем меньше их амплитуда. При очень быстром вращении нутации делаются практически незаметными для глаза.

Может показаться странным: почему гироскоп, будучи раскручен, установлен под углом к вертикали и отпущен, не падает под действием силы тяжести, а движется вбок? Откуда берется кинетическая энергия прецессионного движения?

Ответы на эти вопросы можно получить только в рамках точной теории гироскопам. На самом деле гироскоп действительно начинает падать, а прецессионное движение появляется как следствие закона сохранения момента импульса. В самом деле, отклонение оси гироскопа вниз приводит к уменьшению проекции момента импульса на вертикальное направление. Это уменьшение должно быть скомпенсировано моментом импульса, связанным с прецессионным движением оси гироскопа. С энергетической точки зрения кинетическая энергия прецессии появляется за счет изменения потенциальной энергии гироскопам.

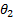
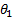
Если за счет трения в опоре нутации гасятся быстрее, чем вращение гироскопа вокруг оси симметрии (как правило, так и бывает), то вскоре после «запуска» гироскопа нутации исчезают и остается чистая прецессия (рис. 9). При этом угол наклона оси гироскопа к вертикали θ 2 оказывается больше, чем он был вначале θ 1 , то есть потенциальная энергия гироскопа уменьшается. Таким образом, ось гироскопа должна немного опуститься, чтобы иметь возможность прецессировать вокруг вертикальной оси.

Гироскопические силы.

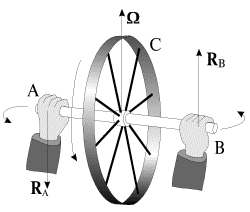
Обратимся к простому опыту: возьмем в руки вал АВ с насаженным на него колесом С (рис. 10). Пока колесо не раскручено, не представляет никакого труда поворачивать вал в пространстве произвольным образом. Но если колесо раскручено, то попытки повернуть вал, например, в горизонтальной плоскости с небольшой угловой скоростью Ω приводят к интересному эффекту: вал стремится вырваться из рук и повернуться в вертикальной плоскости; он действует на кисти рук с определенными силами R_A и R_B (рис. 10). Требуется приложить ощутимое физическое усилие, чтобы удержать вал с вращающимся колесом в горизонтальной плоскости.

Рассмотрим эффекты, возникающие при вынужденном вращении оси гироскопа, более подробно. Пусть ось гироскопа будет укреплена в U-образной раме, которая может поворачиваться вокруг вертикальной оси OO’ (рис. 11). Такой гироскоп обычно называют несвободным — его ось лежит в горизонтальной плоскости и выйти из нее не может.

Раскрутим гироскоп вокруг его вокруг его оси симметрии до большой угловой скорости (момент импульса L ) и станем поворачивать раму с укрепленным в ней гироскопом вокруг вертикальной оси OO’ с некоторой угловой скоростью Ω как показано на рис. 11. Момент импульса L , получит при этом приращение dL которое должно быть обеспечено моментом сил M , приложенным к оси гироскопа. Момент M , в свою очередь, создан парой сил F ÷ F ‘ возникающих при вынужденном повороте оси гироскопа и действующих на ось со стороны рамы. По третьему закону Ньютона ось действует на раму с силами Ф÷ Ф ‘ (рис. 11). Эти силы называются гироскопическими; они создают гироскопический момент M ‘ . Появление гироскопических сил называют гироскопическим эффектом. Именно эти гироскопические силы мы и чувствуем, пытаясь повернуть ось вращающегося колеса (рис.10).

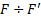
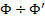
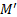
Гироскопический момент нетрудно рассчитать. Положим, согласно элементарной теории, что

L = Jω 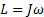(16)

где J — момент инерции гироскопа относительно его оси симметрии, а ω — угловая скорость собственного вращения. Тогда момент внешних сил, действующих на ось, будет равен

M = Ω×L=Ω×(Jω) 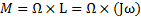(17)

где ω — угловая скорость вынужденного поворота (иногда говорят: вынужденной прецессии). Со стороны оси на подшипники действует противоположный момент

M ‘ =- M = Jω × Ω 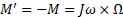(18)

Таким образом, вал гироскопа, изображенного на рис. 11, будет прижиматься кверху в подшипнике В и оказывать давление на нижнюю часть подшипника А.

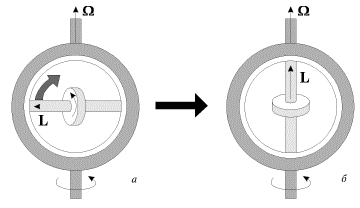
Направление гироскопических сил можно легко найти с помощью правила, сформулированного Н.Е. Жуковским: гироскопические силы стремятся совместить момент импульса L гироскопа с направлением угловой скорости вынужденного поворота. Это правило можно наглядно продемонстрировать с помощью устройства, представленного на рис. 12.

Ось гироскопа закреплена в кольце, которое может свободно поворачиваться в обойме. Приведем обойму во вращение вокруг вертикальной оси с угловой скоростью Ω (вынужденный поворот), и кольцо с гироскопом будет поворачиваться в обойме до тех пор, пока направления L и Ω не совпадут. Такой эффект лежит в основе известного магнитомеханического явления — намагничивания железного стержня при его вращении вокруг собственной оси — при этом спины электронов выстраиваются вдоль оси стержня (опыт Барнетта ).

Гироскопические усилия испытывают подшипники осей быстро вращающихся частей машины при повороте самой машины (турбины на корабле, винта на самолете и т.д.). При значительных величинах угловой скорости вынужденной прецессии Ω и собственного вращения ω а также больших размерах маховика эти силы могут даже разрушить подшипники. Рассмотрим некоторые примеры проявления гироскопических сил.

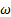
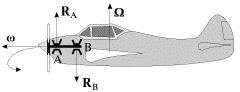
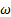
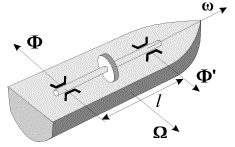
Пример 1. Легкий одномоторный самолет с правым винтом совершает левый вираж (рис. 13). Гироскопический момент передается через подшипники А и В на корпус самолета и действует на него, стремясь совместить ось собственного вращения винта (вектор ω ) с осью вынужденной прецессии (вектор Ω ). Самолет начинает задирать нос кверху, и летчик должен «дать ручку от себя», то есть опустить вниз руль высоты. Таким образом, момент гироскопических сил будет компенсирован моментом аэродинамических сил.

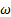
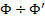
Пример 2. При килевой качке корабля (с носа на корму и обратно) ротор быстроходной турбины участвует в двух движениях: во вращении вокруг своей оси с угловой скоростью ω и в повороте вокруг горизонтальной оси, перпендикулярной валу турбины, с угловой скоростью Ω (рис. 14). При этом вал турбины будет давить на подшипники с силами Ф÷ Ф ‘ лежащими в горизонтальной плоскости. При качке эти силы, как и гироскопический момент, периодически меняют свое направление на противоположное и могут вызвать «рыскание» корабля, если он не слишком велик (например, буксира).

Допустим, что масса турбины m =3000 кг ее радиус инерции R _ин = 0,5 м, скорость вращения турбины n =3000 об/мин, максимальная угловая скорость корпуса судна при килевой качке Ω =5 град/с, расстояние между подшипниками l =2 м. Максимальное значение гироскопической силы, действующей на каждый из подшипников, составляет

Ф= M l = JwΩ l = m R ин 2 ∙2 πn ∙ Ω l (19)

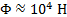
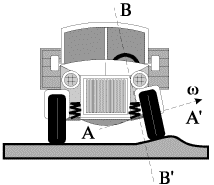
После подстановки числовых данных получим Ф≈ 10 4 Н то есть около 1 тонны.

Пример 3. Гироскопические силы могут вызвать так называемые колебания «шимми» колес автомобиля (рис. 15) [В.А. Павлов, 1985]. Колесу, вращающемуся вокруг оси AA’ с угловой скоростью w в момент наезда на препятствие сообщается дополнительная скорость вынужденного поворота вокруг оси, перпендикулярной плоскости рисунка. При этом возникает момент гироскопических сил, и колесо начнет поворачиваться вокруг оси BB’. Приобретая угловую скорость поворота вокруг оси BB’, колесо снова начнет поворачиваться вокруг оси, перпендикулярной плоскости рисунка, деформируя упругие элементы подвески и вызывая силы, стремящиеся вернуть колесо в прежнее вертикальное положение. Далее ситуация повторяется. Если в конструкции автомобиля не принять специальных мер, возникшие колебания «шимми» могут привести к срыву покрышки с обода колеса и к поломке деталей его крепления.

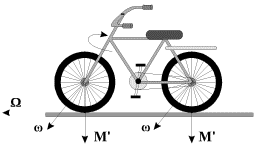
Пример 4. С гироскопическим эффектом мы сталкиваемся и при езде на велосипеде (рис. 16). Совершая, например, поворот направо, велосипедист инстинктивно смещает центр тяжести своего тела вправо, как бы заваливая велосипед. Возникшее принудительное вращение велосипеда с угловой скоростью Ω приводит к появлению гироскопических сил с моментом M ‘ . На заднем колесе этот момент будет погашен в подшипниках, жестко связанных с рамой. Переднее же колесо, имеющее по отношению к раме свободу вращения в рулевой колонке, под действием гироскопического момента начнет поворачиваться как раз в том направлении, которое было необходимо для правого поворота велосипеда. Опытные велосипедисты совершают подобные повороты, что называется, «без рук».

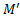
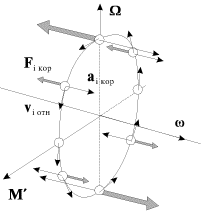
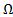
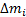
Вопрос о возникновении гироскопических сил можно рассматривать и с другой точки зрения. Можно считать, что гироскоп, изображенный на рис. 11, участвует в двух одновременных движениях: относительном вращении вокруг собственной оси с угловой скоростью w и переносном, вынужденном повороте вокруг вертикальной оси с угловой скоростью Ω . Таким образом, элементарные массы Δ m i , на которые можно разбить диск гироскопа (маленькие кружки на рис. 17), должны испытывать кориолисовы ускорения

a i кко =2 Ω × v i оот 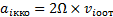(20)

Эти ускорения будут максимальны для масс, находящихся в данный момент времени на вертикальном диаметре диска, и равны нулю для масс, которые находятся на горизонтальном диаметре (рис. 17).

В системе отсчета, вращающейся с угловой скоростью Ω (в этой системе отсчета ось гироскопа неподвижна), на массы Δ m i будут действовать кориолисовы силы инерции

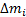
F i кко =2 Δ m i v отн × Ω 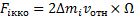(21)

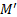
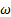
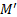
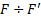
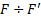
Эти силы создают момент M ‘ который стремится повернуть ось гироскопа таким образом, чтобы вектор Ω совместился с ω . Момент M ‘ должен быть уравновешен моментом сил реакции F ÷ F ‘ действующих на ось гироскопа со стороны подшипников. По третьему закону Ньютона, ось будет действовать на подшипники, а через них и на раму, в которой эта ось закреплена, с гироскопическими силами F ÷ F ‘ . Поэтому и говорят, что гироскопические силы обусловлены силами Кориолиса.

Возникновение кориолисовых сил можно легко продемонстрировать, если вместо жесткого диска (рис. 17) взять гибкий резиновый лепесток (рис. 18). При повороте вала с раскрученным лепестком вокруг вертикальной оси лепесток изгибается при прохождении через вертикальное положение так, как изображено на рис. 18.

Волчки.

Волчки кардинально отличаются от гироскопов тем, что в общем случае они не имеют ни одной неподвижной точки. Произвольное движение волчков имеет весьма сложный характер: будучи раскручены вокруг оси симметрии и поставлены на плоскость, они прецессируют , «бегают» по плоскости, выписывая замысловатые фигуры, а иногда даже переворачиваются с одного конца на другой. Не вдаваясь в детали такого необычного поведения волчков, отметим лишь, что немаловажную роль здесь играет сила трения, возникающая в точке соприкосновения волчка и плоскости.

Кратко остановимся на вопросе об устойчивости вращения симметричного волчка произвольной формы. Опыт показывает, что если симметричный волчок привести во вращение вокруг оси симметрии и установить на плоскость в вертикальном положении, то это вращение в зависимости от формы волчка и угловой скорости вращения будет либо устойчивым, либо неустойчивым.

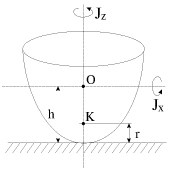
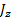
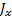
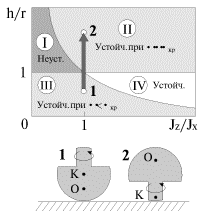
Пусть имеется симметричный волчок, изображенный на рис. 19. Введем следующие обозначения: О — центр масс волчка, h — расстояние от центра масс до точки опоры; K — центр кривизны волчка в точке опоры, r — радиус кривизны; J z — момент инерции относительно оси симметрии, J x — момент инерции относительно главной центральной оси, перпендикулярной оси симметрии.

Анализ устойчивости вращения волчка приводит к диаграмме, изображенной на рис. 20. Здесь по оси абсцисс отложено отношение J z / J x 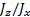, а по оси ординат – отношение h / r .

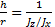
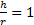
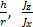
Проведем гиперболу h r = 1 J z / J x и прямую h r =1 . Эти линии делят область положительных значений h r , J z J x на 4 части.

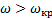
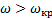
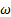
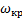
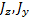
Область I соответствует неустойчивому вращению волчка при всех угловых скоростях, область II — устойчивому вращению при достаточно больших угловых скоростях ω > ω кр . Область III соответствует устойчивому вращению при малых угловых скоростях ω > ω кр , область IV — устойчивому вращению при произвольных ω . Критическая угловая скорость ω кр зависит от моментов инерции J z , J y , расстояний r , h и веса тела P = mg [К. Магнус , 1974]:

w кр 2 = (h- r )∙ P J x ( r /h)∙( J z / J x — r /h) (22)

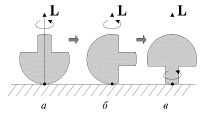
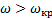
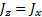
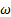
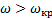
Рассмотрим, например, китайский волчок, раскрученный до ω > ω кр и поставленный на плоскость вертикально, как показано на рис. 20, а. Пусть J z = J x . Поскольку h r то этой ситуации соответствует точка 1 в области III на рис. 19, то есть область устойчивого вращения лишь при малых ω . Таким образом, в нашем случае ω > ω кр вращение будет неустойчивым, и волчок перевернется на ножку (точка 2 в области II на рис. 20).

Следует обратить внимание, что в процессе переворачивания волчка результирующий момент импульса сохраняет свое первоначальное направление, то есть вектор L , все время направлен вертикально вверх. Это означает, что в ситуации, изображенной на рис. 21, б, когда ось волчка горизонтальна, вращение вокруг оси симметрии волчка отсутствует! Далее, при опрокидывании на ножку, вращение вокруг оси симметрии будет противоположно исходному (если смотреть все время со стороны ножки, рис. 21, в).

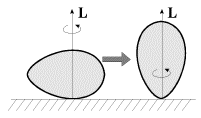
В случае яйцеобразного волчка поверхность тела в окрестности точки опоры не является сферой, но существуют два взаимно перпендикулярных направления, для которых радиус кривизны в точке опоры принимает экстремальные (минимальное и максимальное) значения. Опыты показывают, что в случае, изображенном на рис. 21, а, вращение будет неустойчивым, и волчок принимает вертикальное положение, раскручиваясь вокруг оси симметрии и продолжая устойчивое вращение на более остром конце. Это вращение будет продолжаться до тех пор, пока силы трения не погасят в достаточной мере кинетическую энергию волчка, угловая скорость уменьшится (станет меньше ω ₀ ), и волчок упадет.

Вопросы для самопроверки

— Какое твердое тело называют гироскопом?

— Чему равен и как направлен кинетический момент быстровращающегося гироскопа относительно его неподвижной точки?

— Какими физическими свойствами обладает быстровращающийся гироскоп с тремя степенями свободы?

— Какой эффект производит действие одной и той же силы, приложенной к оси неподвижного и быстровращающегося гироскопа с тремя степенями свободы?

— Выведите формулу для вычисления угловой скорости прецессии оси гироскопа.

— В чем состоит разница в свойствах гироскопов с двумя и тремя степенями свободы?

— Какова физическая сущность гироскопического эффекта и при каких условиях он наблюдается?

— По каким формулам определяются динамические реакции подшипников, в которых вращается рама вращающегося гироскопа с двумя степенями свободы?

1. А.Н. Матвеев. Механика и теория относительности. М.: Высшая школа, 1986.

2. С.П. Стрелков. Механика. М.: Наука, 1975.

3. С.Э. Хайкин. Физические основы механики. М.: Наука, 1971.

4. Д.В. Сивухин . Общий курс физики. Т.1. Механика. М.: Наука, 1989.

5. Р.В. Поль. Механика, акустика и учение о теплоте. М.: Наука, 1971.

6. Р. Фейнман и др. Фейнмановские лекции по физике. М.: Мир, 1977.

7. Ч. Киттель , У. Найт , М. Рудерман . Механика. М.: Наука, 1983.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Видео:Гироскоп и его применениеСкачать

ГИРОСКО́П

В книжной версии

Том 7. Москва, 2007, стр. 177-180

Скопировать библиографическую ссылку:

ГИРОСКО́П (от греч. γῦρος – круг, окружность и σϰοπέω – наблюдать), устройство, совершающее быстрые циклические (вращательные или колебательные) движения и чувствительное вследствие этого к повороту в инерциальном пространстве. Термин «Г.» предложен в 1852 Ж. Б. Л. Фуко для изобретённого им прибора, предназначенного для демонстрации вращения Земли вокруг своей оси. Долгое время термин «Г.» использовался для обозначения быстровращающегося симметричного твёрдого тела. В совр. технике Г. – осн. элемент всевозможных гироскопич. устройств или приборов, широко применяемых для автоматич. управления движением самолётов, судов, торпед, ракет, космич. аппаратов, мобильных роботов, для целей навигации (указатели курса, поворота, горизонта, стран света), для измерения угловой ориентации подвижных объектов и во многих др. случаях (напр., при прохождении стволов штолен, строительстве метрополитенов, при бурении скважин).

Видео:ГироскопСкачать

гироскоп

ГИРОСКОП (от греч. gyreuо — кружусь, вращаюсь и skopeo — смотрю, наблюдаю) — быстровращающееся симметричное твёрдое тело, ось вращения (ось симметрии) к-рого может изменять своё направление в пространстве. Свойствами Г. обладают вращающиеся небесные тела, артиллерийские снаряды, роторы турбин, устанавливаемых на судах, винты самолётов и т. п. В совр. технике Г.- осн. элемент всевозможных гироскопич. устройств или приборов, широко применяемых для автоматич. управления движением самолётов, судов, торпед, ракет и в ряде др. систем гироскопич. стабилизации, для целей навигации (указатели курса, поворота, горизонта, стран света и др.), для измерения угловых или поступат. скоростей движущихся объектов (напр., ракет) и во мн. др. случаях (напр., при прохождении стволов штолен, строительстве метрополитенов, при бурении скважин).

Чтобы ось Г. могла свободно поворачиваться в пространстве, Г. обычно закрепляют в кольцах т. н. карданова подвеса (рис. 1), в к-ром оси внутр. и внеш. колец и ось Г. пересекаются в одной точке, наз. центром подвеса. Закреплённый в таком подвесе Г. имеет 3 степени свободы и может совершать любой поворот около центра подвеса. Если центр тяжести Г. совпадает с центром подвеса, Г. наз. уравновешенным, или астатическим. Изучение законов движения Г.- задача динамики твёрдого тела.

Рис. 1. Классический карданов подвес, а — внешнее кольцо, б — внутреннее кольцо, в — ротор.

Рис. 2. Прецессия гироскопа. Угловая скорость прецессии направлена так, что вектор собственного кинетического момента Н стремится к совмещению с вектором момента М пары, действующей на гироскоп.

Основные свойства гироскопа. Если к оси быстровращающегося свободного Г. приложить пару сил (P — F)с моментом (h — плечо силы) (рис. 2), то (против ожидания) Г. начнёт дополнительно поворачиваться не вокруг оси х, перпендикулярной к плоскости пары, а вокруг оси у, лежащей в этой плоскости и перпендикулярной к собств. оси тела z. Это дополнит. движение наз. прецессией. Прецессия Г. будет происходить по отношению к инерциалъной системе отсчета (к осям, направленным на неподвижные звёзды) с угловой скоростью

где I — момент инерции Г. относительно оси z, — угловая скорость собств. вращения Г. относительно той же оси. Величина наз. собственным кинетическим моментом (или моментом количества движения)Г. Направление определяется так, как показано на рис. 2. Из ф-лы (1) ясно, что прецессия происходит тем медленнее, чем больше ; на практике величинабывает в миллионы раз меньше .

Рис. 3. Конус нутаций.

При более подробном рассмотрении оказывается, что собств. вращение и прецессия симметричного Г. могут сопровождаться т. н. нутациями — быстрыми конич. движениями оси Г. относительно изменяющегося по закону (1) направления (рис. 3). Угол конуса нутации , как правило, бывает очень мал. Кроме того, из-за наличия неизбежных сопротивлений нутации обычно быстро затухают. Всё это позволяет при решении большинства технич. задач учитывать только прецессию Г., что и приводит к т. н. элементарной, или прецессионной, теории гироскопич. явлений, осн. соотношением к-рой является ф-ла (1). В более общем случае, когда угол а между осями собств. вращения и прецессии оказывается не равным 90°, эта ф-ла принимает вид

При изучении поведения Г. по отношению к подвижному основанию в выражение для M должны входить и моменты сил инерции переносного движения.

Из ф-лы (1) следует, что если Г. будет полностью свободен от постоянно действующих на него сил, т. е. при M=0, ось Г. будет сохранять неизменное направление по отношению к неподвижным звёздам, т. к. тогда =0. Кратковрем. воздействие на ось такого Г. пары сил с моментом вызовет смещение оси на малый угол, тем меньший, чем меньше , т. е. чем больше будет . С прекращением же этого воздействия будет опять M=0, а следовательно, и =0, так что смещение оси прекратится. Т.о., ось быстровращающегося свободного Г. практически не изменяет своего направления под влиянием кратковрем. внеш. возмущений (толчков) и в этом смысле устойчива. Важным свойством свободного Г. устойчиво сохранять направление своей оси пользуются в устройствах, применяемых для автоматич. управления движением самолётов, ракет и т. п., а также в ряде навигац. и др. приборов.

Г., ось к-рого закреплена подшипниками a, a₁ в кольце с неподвижной осью вращения bb₁ (рис. 4), обладает двумя степенями свободы. Если это кольцо вращать вокруг оси bb₁ с угловой скоростью , то Г. будет совершать вынужденную прецессию. При этом со стороны Г. на подшипники a, а₁ действует пара сил (Q, Q₁), стремящаяся совместить ось собств. вращения aа₁ с осью прецессии bb₁ так, чтобы направления векторов и совпали (правило H. E. Жуковского). Момент этой гироскопич. пары

где— угол между осями аa₁ и bb₁. Подобный гироскопич. эффект имеет место у роторов турбин, установленных на судах, при повороте судов или при качке, у винтовых самолётов при виражах и т. п. Ф-ла (3) позволяет определить возникающие при этом гироскопич. давления на подшипники.

На гироскопич. эффекте основан принцип т. н. силовой гироскопич. стабилизации (см. ниже), а также устройство ряда приборов, напр. гироскопич. указателя поворотов и др.

Уравнения движения гироскопа. Движение большинства гироскопич. систем таково, что если исключить кратковрем. переходные процессы, возникающие при ударах или при резких изменениях сил, действующих на систему, изменение ориентации осей роторов Г. относительно направлений на неподвижные звёзды происходит весьма медленно. При изучении такого прецессионного движения достаточно пользоваться элементарной теорией Г.

Рис. 4. Гироскоп с двумя степенями свободы.

Исследование процессов, в течение к-рых оси роторов Г. совершают нутации, и решение вопросов устойчивости гироскопич. систем требуют учёта кинетич. моментов всех тел, входящих в состав гироскопич. системы. Соответствующие ур-ния движения являются ур-ниями нутац. теории Г. Дифференц. ур-ния нутац. теории имеют для данной гироскопич. системы более высокий порядок, чем ур-ния прецессионного движения. Однако решение задач нутац. теории упрощается тем обстоятельством, что во мн. случаях можно ограничиться рассмотрением малых движений методами теории малых колебаний.

Строго ур-ния движения Г. справедливы по отношению к инерциальной системе отсчёта, однако на практике движение гироскопич. систем приходится изучать по отношению к осям, связанным с тем подвижным объектом (судно, самолёт, ракета, Земля и др.), на к-ром эти системы установлены. Поэтому при составлении ур-ний в число действующих сил надлежит включать также переносные и Кориолиса силы, инерции, обусловленные перемещением объекта. Оказывается, что удобнее всего составлять ур-ния движения Г. по отношению к системе координат с началом в центре 0 подвеса гироскопич. системы и с осями, не изменяющими своей ориентации относительно направлений на неподвижные звёзды, т. е. перемещающимися по отношению к инерциальной системе отсчёта поступательно. В этом случае кориолисовы силы инерции вообще отсутствуют, а все силы инерции переносного движения антипараллельны ускорению центра 0 в его движении относительно инерциальной системы отсчёта.

Рис. 5. Приложение теоремы механики системы о кинетическом моменте к установлению уравнения прецессионного движения ротора гироскопа. Скорость конца вектора собственного кинетического момента принимается геометрически равной главному моменту совокупности сил, приложенных к ротору.

В теории Г. с достаточным для практики приближением можно за инерциальную систему отсчёта принять невращающуюся систему координат с началом в центре Земли. Точно так же малая погрешность при подсчёте сил инерции переносного движения происходит, если за ускорение центра 0 подвижной невращающейся системы координат принять его ускорение относительно земной поверхности. В этом случае вместо действующих на массы частей гироскопич. системы сил тяготения к Земле следует брать силы тяжести. Для составления ур-ний движения Г. введём ещё систему осей 0x’y’z’ с началом в той же точке 0, что и у системы 0 (точка 0 лежит где-то на оси симметрии ротора, напр. в центре его подвеса). Ось z‘ системы совпадает с осью симметрии ротора, но сама система Ox’y’z’ не вращается вместе с ротором, будучи связанной, напр., с кожухом Г. Тогда ур-ния прецессионного движения ротора, симметричного Г. относительно осей , записанные в проекциях на оси Ox’y’z’, имеют вид

Они выражают (рис. 5) равенство (по числ. величине и направлению) скорости конца вектора собственного кинетич. момента и гл. момента относительно центра 0 сил, приложенных к ротору. В число этих сил должны быть включены переносные силы инерции, обусловленные поступат. движением системы отсчёта О . Величины и — проекции на оси х’ и у’ угловой скорости системы координат Ox’y’z’ относительно системы , т. е. относительно направлений на неподвижные звёзды. Угловую скорость ротора относительно осей Ox’y’z’ можно наз. угловой скоростью его собств. вращения. Вектор Н направлен по оси собств. вращения (рис. 6> ротора z’, а его модуль можно принять равным

где С — момент инерции ротора относительно его оси симметрии z’ (полярный момент инерции), — угол поворота ротора относительно системы координат x’y’z’. Принимается также, что значительно превышает величину — проекцию угловой скорости системы координат на её же ось (на практике на 3-4 порядка). В большинстве случаев Н можно считать постоянным, т. к. обычно моменты сил, вращающих ротор, и моменты сопротивления этому вращению взаимно уравновешиваются. Соответственно, в 3-м из ур-ний (4) следует положить М_z’=0.

Рис. 6. Вектор собственного кинетического момента гироскопа. Система координат аbс связана с ротором гироскопа; она вращается относительно системы x’y’z’ с угловой скоростью вокруг оси z’, совпадающей с осью с. Момент инерции ротора относительно оси с (оси симметрии или оси собственного вращения) обозначен через С.

Более строгими ур-ниями движения ротора являются ур-ния, соответствующие нутац. теории Г., а именно:

где А — момент инерции ротора относительно к—л. оси, перпендикулярной его оси симметрии и проходящей через центр О (экваториальный момент инерции). В ур-ниях (6), в отличие от ур-ний (4), принято, что система координат x’y’z’ может иметь угловую скорость с произвольной составляющей вдоль оси симметрии ротора z’. B частности, эту систему можно связать с самим ротором. Тогда ур-ния обращаются в общеизвестные ур-ния Эйлера движения твёрдого осесимметричного тела (см. Эйлера динамические уравнения), осложнённые наличием в правых частях упоминавшихся выше переносных сил инерции.

Ур-ния (4) и (6) пригодны для изучения движения ротора Г., не стеснённого кардановым подвесом, напр. в случае шарового Г. (см. ниже), и вообще свободных тел (снаряд, небесные тела, искусств. спутники, космич. корабли). При наличии же карданова подвеса в состав сил, образующих моменты относительно осей х’ и у’, т. е. в выражения для М_х’ и M_y’ , войдут неизвестные силы — нормальные реакции подшипников оси ротора. Для исключения этих сил, представляющих воздействие внутр. кольца подвеса (кожуха) на ротор, следует совместно с ур-ниями движения ротора рассматривать также и ур-ния движения элементов подвеса Г.

При составлении ур-ний прецессионного движения Г. в кардановом подвесе изменение кинетич. моментов элементов подвеса не учитывается. Поэтому совокупность сил, приложенных, напр., к внутр. кольцу подвеса (кожуху), следует считать статически эквивалентной нулю (уравновешенной). T. о., вместо ур-ний движения внутр. кольца фактически составляются ур-ния равновесия всех приложенных к нему сил, т. е. сил взаимодействия с внеш. кольцом, ротором Г. и его основанием, сторонних (внеш.) сил и сил инерции переносного движения. То же относится и к силам, приложенным к внеш. кольцу карданова подвеса.

После исключения нормальных реакций осей подвеса ур-ния прецессионного движения Г. в кардановом подвесе приводятся к виду

Здесь т_х’ , т_y’ , m_z’ — суммы моментов относительно осей х’, у’, z’ соответственно всех сторонних сил и сил инерции переносного движения, действующих на ротор; I_х’ ,I_y’ ,I_z’ — аналогичные суммы, относящиеся к внутр. кольцу подвеса (кожуху); M — сумма моментов относительно оси z’ сил, действующих на ротор со стороны внутр. кольца (кожуха), т. е. сил, вращающих ротор, и сил сопротивления этому вращению (сил трения); L — сумма моментов относительно оси у’ (или ) кожуха (рис. 7) сил воздействия внеш. кольца карданова подвеса на внутр. кольцо (кожух); К — сумма моментов относительно оси (или ) внеш. кольца сил воздействия основания Г. на это кольцо; k — аналогичная сумма моментов сторонних сил, действующих на внеш. кольцо; — угол поворота внутр. кольца (кожуха) относительно внешнего. Он принимается положительным, если система координат x’y’z’, связанная с внутр. кольцом (кожухом), повёрнута относительно системы координат , связанной с внешним кольцом подвеса, против хода часовой стрелки (наблюдение за поворотом производится со стороны положит. части оси у’ или ). При=0 оси этих систем соответственно совпадают.

Рис. 7. Схема гироскопа в кардановом подвесе. Система координат x’y’z’ связана с внутренним кольцом подвеса, система -с внешним, а -с основанием гироскопа (на рис. показана лишь ось ).

Для определения величин , следует знать угловые скорости: основания Г. относительно системы координат , внеш. кольца карданова подвеса по отношению к основанию и внутр. кольца по отношению к внешнему. Имеют место след. ф-лы:

где — проекции угловой скорости основания Г. на оси, связанной с основанием системы координат . Осьэтой системы совпадает с осью внеш. кольца подвеса. Угол поворота внеш. кольца относительно основания обозначен через (рис. 8). При =0 оси систем координат соответственно совпадают. Положит. направление отсчёта угла такое же, как и угла. Ур-ния (7) и (8) позволяют решать большинство вопросов, связанных с одногироскопными гироскопическими системами в рамках прецессионной теории гироскопа.

Рис. 8. К подсчёту абсолютной угловой скорости внутреннего кольца карданова подвеса (система координат x’y’z’). Вектор — относительная угловая скорость внешнего кольца относительно основания , — угловая скорость внутреннего кольца относительно внешнего.

Рис. 9. Полюс гироскопа (точка P) и связь составляющих его скорости v_x и v_y относительно невращающейся системы координат (на рис не показана) с суммами M_x и M_y моментов сил, действующих на ротор гироскопа и его внутреннее кольцо (кожух).

В случае, когда можно пренебречь моментами трения К и L в осях подвеса и считать равными нулю моменты k, т_z , l_z и М, ур-ния прецессионной теории Г. в кардановом подвесе значительно упрощаются и допускают следующую геометрич. интерпретацию. Вводится вспомогат. система координат xyz с началом в центре подвеса Г. (рис. 9). На расстоянии, равном единице от начала координат, строится плоскость, параллельная координатной плоскости ху. Через х и у обозначаются координаты точки P пересечения вектора H с упомянутой плоскостью (полюс Г.). Тогда ур-ния прецессионного движения Г. можно представить в виде:

где v_x и v_y — проекции на оси х и у скорости точки P в её движении по отношению к системе координат . Модуль H в данном случае — пост. величина. Предполагается, что направление H мало отклоняется от направления оси z, в результате чего координаты х и у точки P малы по сравнению с единицей и с большой точностью равны углам отклонения от координатных плоскостей yz и xz вектора H или, что то же, оси собств. вращения гироскопа z.

Величины M_х и M_у, к-рые находятся в правых частях ур-ний (9), представляют собой суммы моментов относительно осей х и у сторонних сил и переносных сил инерции, действующих на механич. систему: ротор — внутр. кольцо (кожух) Г.

Если обозначить через проекции на оси х, у, z угловой скорости системы координат х у z относительно невращающейся системы , то ур-ния (9) можно представить в виде

Полученные ур-ния удобны для исследования поведения однороторного гирокомпаса, гироскопич. маятника (гировертикали) при смещениях основания, на к-ром они расположены. В первом случае ось z направляется на север, а во втором — вертикально.

Ур-ния движения Г. в кардановом подвесе, соответствующие нутац. теории, можно также вывести, пользуясь Лагранжа уравнениями 2-го рода. При этом следует рассматривать движение механич. системы, состоящей из ротора и элементов подвеса Г. по отношению к невращающейся системе координат с началом в центре карданова подвеса, и принять углы за обобщённые координаты упомянутой механич. системы. Составив ур-ния для её кинетич. энергии, с помощью ур-ний Лагранжа 2-го рода можно получить ур-ния движения, позволяющие изучать поведение Г. в разл. гироскопич. устройствах.

Устойчивость гироскопа. Г. с тремя степенями свободы, находящийся под длит. воздействием сил, устойчив не всегда. Напр., вертикальный («спящий») волчок, испытывающий воздействие силы тяжести (рис. 10), устойчив только при выполнении условия

где P — вес Г., а — расстояние его центра тяжести от точки опоры О, А — момент инерции Г. относительно оси Ox. При невыполнении этого условия ось Г. будет удаляться от вертикали, совершая петлеобразные движения. Аналогичное условие имеет место и для устойчивости прецессионного движения Г. Напр., устойчивость при движении в воздухе вращающегося артиллерийского снаряда приближённо определяется ф-лой H. В. Маиевского, к-рая совпадает с (11), если в ней под P понимать силу сопротивления воздуха, а под а — расстояние от центра масс С до точки О пересечения линии действия силы P с осью снаряда (рис. 11). Г. с двумя степенями свободы (рис. 4) всегда неустойчив; при толчке, дающем момент относительно оси bb₁, такой Г. начнёт вращаться вместе с кольцом вокруг этой оси.

Гироскопы в технике. Применяемые в технике Г. представляют собой тела вращения (роторы), имеющие обычно форму маховика с утолщенным ободом или шара массой от неск. г до десятков кг. Быстрое вращение Г. (со скоростью до 60 000 об/мин и более) обычно достигается тем, что ротор Г. делают вращающейся частью (ротором) быстроходного электродвигателя пост. или переменного тока. Иногда вращение Г. поддерживается струёй воздуха — ротор Г. является одновременно ротором возд турбинки. К основанию прибора (устройства) Г. крепится с помощью той или иной системы подвеса. Наиболее употребителен карданов подвес с ротором, заключенным в кожух. Для уменьшения сопротивления вращению в ряде случаев кожух делается герметичным и заполняется водородом. Это способствует также предотвращению коррозии металлич. частей и окисления смазки. В нек-рых приборах кожух, заключающий в себе ротор Г., погружают в жидкость. Подшипники кожуха (поплавка) при этом почти полностью разгружаются и момент трения скольжения в них уменьшается до стотысячных долей. H*см. Применяются также проволочные (торсионные) подвесы и подвесы на возд. плёнке, напр. у т.н. шара-гироскопа (рис. 12).

Рис. 10. «Спящий» волчок.

Рис. U. К устойчивости вращающегося снаряда.

Рис. 12. Шар-гироскоп Сперри на воздушном подвесе, а-стальной ротор, б-статор, создающий вращающее магнитное поле; в — датчик, посредством сигналов к-рого производится «слежение» за осью шара на качающемся основании (корабле); г — бронзовая чаша, отделённая от шара воздушным слоем толщиной порядка сотых долей мм, д — подача сжатого воздуха для поддержки шарагироскопа.

Важным элементом мн. гироскопич. приборов является уравновешенный Г. с тремя степенями свободы. Для повышения точности прибора требуется максимально уменьшать величину момента M, возникающего вследствие трения в осях подвеса и несовпадения центра тяжести ротора с центром подвеса, т. к., согласно ф-ле (1), этот момент вызывает прецессию (уход) оси ротора. Момент трения в подвесах точных (прецизионных) Г. обычно уменьшают применением высококачеств. шариковых подшипников. Вследствие вибраций подвеса или возвратно-вращат. движений внеш. обоймы шарикоподшипников момент трения в ряде случаев удаётся сделать значительно меньше момента силы тяжести. Уменьшение момента силы тяжести достигается соответствующей балансировкой Г. Требуемая при этом точность совмещения центра масс Г. с геом. центром подвеса очень велика. Так, для Г. ср. размеров массой ок. 1 кг, имеющего угловую скорость вращения ротора порядка 30 000 об/мин, смещение центра масс от осп подвеса на 1 мк вызывает прецессию со скоростью ок. 1 град/ч. Земля вращается со значительно большей угловой скоростью — 15 град/час. Следовательно, подобным Г. можно легко обнаружить факт вращения Земли. Однако для решения ряда технич. вопросов, напр. навигации судов и ракет, требуется еще более высокая точность балансировки, т. к. скорость ухода оси Г. относительно неподвижных звёзд порядка 1 град/ч оказывается чрезмерно большой. Улучшая балансировку и уменьшая трение в осях, а также увеличивая кинетич. момент H, удаётся в соответствии с ф-лой (1) достичь медленного ухода оси и обеспечить тем самым необходимую точность работы разл. гироскопич. приборов, в частности приборов управления движением баллистич. ракет и систем инерциальной навигации.

В обычных Г. имеются два разл. вида подшипников: подшипники, в к-рых совершает быстрое вращение ротор, и подшипники подвеса. Подшипники оси собств. вращения ротора должны обладать достаточной жёсткостью, высокой долговечностью при работе на больших скоростях вращения. Подшипники же подвеса работают при малых угловых скоростях и осн. требование к ним — иметь возможно меньшее трение.

Среди современных типов Г., в к-рых проблема опор решается иначе, чем в классич. схеме «ротор в кардановом подвесе», следует упомянуть т. н. динамически настраиваемый Г. В нём быстровращающийся ротор посредством упругих связей и промежуточных инерц. элементов крепится к валу. Спец. подбором параметров (условие динамич. настройки) добиваются равенства нулю (в среднем) моментов, вызывающих прецессию оси ротора в пределах малых углов её отклонения от оси вала ротора. В результате ось ротора практически оказывается неподвижной в инерциальном пространстве. Преимуществом этих Г. является отсутствие специфич. моментов трения в подшипниках подвеса, а также возможность увеличения кинетич. момента ротора при неизменных габаритах прибора.

Стремление получить Г. более высокой точности привело к созданию электростатич. и магн. подвесов. В этих Г. быстровращающийся шар поддерживается электрич. или магн. полем в вакууме. T. к. из камеры, в к-рой находится вращающееся тело, газ полностью выкачан, то тело практически не испытывает трения и может вращаться по инерции в течение неск. нед.

В случае электростатич. подвеса поверхность шара выполняется из диэлектрика, и поддерживающее электрич. поле индуцирует на нём электрич. заряды противоположного знака, в результате чего всегда возникает притягивающая сила. Для подвешивания тел это свойство непосредственно использовать нельзя, т. к., согласно Ирншоу теореме, статич. равновесие тел, притягивающихся друг к другу по закону обратных квадратов, всегда неустойчиво. Для создания устойчивого подвеса используют регулируемое поле. То же самое имеет место и для магн. подвесов, когда ротор выполняется из ферромагнетика. Если же ротор изготавливать из диамагн. материала, то подвес может быть устойчивым и без дополнит. регулирования магн. поля (пассивный подвес). Эта схема подвеса нашла применение в т. н. криогенном Г., в к-ром в условиях сверхнизких темп-р материал шара — ниобий — переходит в сверхпроводящее состояние, при этом он становится идеальным диамагнетиком. Внутрь такого материала магн. поле не проникает. Само поле создаётся токами, циркулирующими в сверхпроводнике без потерь.

Перспективными датчиками инерциальной информации являются лазерный Г. и волновой твердотельный Г., принцип действия к-рых основан на инерционности образующихся в них стоячих волн — электромагнитных в лазерном Г. и упругих в твердотельном. В лазерных Г. используют два луча света от источника когерентного излучения, распространяющиеся в противоположных направлениях по замкнутому кольцевому контуру. При вращении основания, на к-ром установлен Г., между лучами возникает разность фаз, что позволяет обнаружить это вращение и найти его угловую скорость или угол поворота.