Куб параллельные прямые пересекающиеся прямые

ПРЯМАЯ ПРИЗМА. ПОВЕРХНОСТЬ И ОБЪЁМ ПРЯМОЙ ПРИЗМЫ.

1. Построение модели куба.

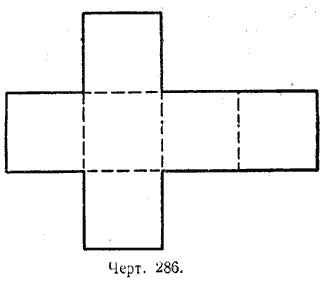
На чертеже 286 изображена выкройка, или, как её принято называть, развёртка геометрического тела. Она состоит из шести равных квадратов. Если эту развёртку согнуть надлежащим образом по указанным на чертеже пунктирным линиям, то мы получим геометрическое тело, называемое кубом.

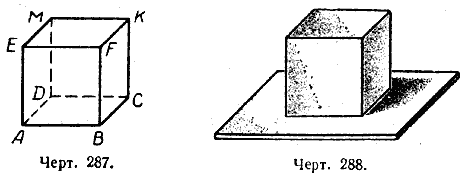
Под номером 287 дан чертёж куба, а под номером 288 дан рисунок куба. Куб ограничен шестью равными квадратами, которые называются его гранями.

На рисунке видны только три его грани, а на чертеже можно видеть все шесть граней. Любые две противоположные грани куба называются его основаниями, тогда остальные четыре его грани называются боковыми гранями; отрезки, которые получаются при пересечении граней куба, называются его рёбрами. У куба 12 рёбер. Все они равны между собой.При пересечении трёх граней куба образуются точки, которые называются его в е р ш и н а м и. У куба 8 вершин.

2. Взаимное положение рёбер и граней куба.

Противоположные грани куба параллельны. Плоскости, в которых лежат эти грани, не пересекаются, т. е. не имеют общих точек. Параллельные плоскости мы наблюдаем на многих окружающих нас предметах; например, плоскости пола и потолка в комнате параллельны.
В кубе можно наблюдать и пересекающиеся плоскости. Пересекаясь, плоскости образуют двугранные углы. Модель двугранных углов можно получить, сгибая лист картона или бумаги по прямой линии.

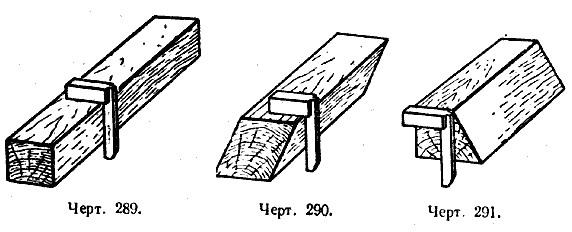
Двугранные углы можно получить острые, прямые и тупые. Грани куба пересекаются под прямым углом. Под прямым углом пересекаются также стены в комнате, стены и потолок, стены и пол. Плоскости, пересекающиеся под прямым углом, называются перпендикулярными. Перпендикулярность плоскостей проверяется с помощью угольника. На чертеже 289 плоскости при пересечении образуют прямой угол. На чертеже 290 и на чертеже 291 показаны плоскости, которые при пересечении не образуют прямого угла; в первом случае они пересекаются под острым углом, во втором случае — под тупым.

Рёбра куба, находящиеся на одной грани (черт. 287), или пересекаются под прямым углом (ЕА _|_ АВ, КС _|_ ВС и т. д.), или параллельны (ЕF || АВ, ВС || КF и т. д.).

3. Скрещивающиеся прямые.

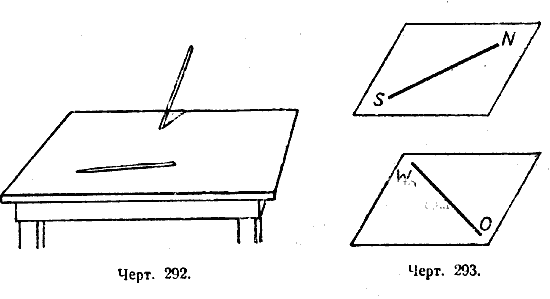
Рёбра куба, например КС и АВ (черт. 287), не параллельны, но и не пересекутся, сколько бы их ни продолжать. Прямые, которые не параллельны и не пересекаются, называются скрещивающимися. Легко получить модели скрещивающихся прямых. Например, две иглы, из которых одна положена на стол, а другая воткнута в стол так, что не пересекает первую, представляют собой модель двух скрещивающихся прямых (черт. 292). Эти две прямые не пересекаются и не параллельны; легко убедиться, что через них нельзя провести плоскость.

Точно так же, если взять две дощечки, поместить их параллельно друг другу и затем на одну из них положить палочку в направлении, например, с юга на север, а на другую — в направлении с запада на восток, то эти две палочки образуют модель скрещивающихся прямых (черт. 293).

Эти две прямые тоже не пересекаются, не параллельны, и через них также нельзя провести плоскость.

Найдите модели скрещивающихся прямых на окружающих предметах, например, в классной комнате.

4. Прямая, перпендикулярная к плоскости.

Рассматривая куб (черт. 287), заметим, что ребро FВ образует прямые углы с рёбрами ВС и АВ, лежащими на нижнем основании куба. Это же ребро FВ образует прямые углы с любой прямой, проведённой в плоскости основания куба через точку В. Ребро FВ является перпендикуляром к плоскости основания куба.

Перпендикуляром к плоскости называется прямая, которая пересекает плоскость в какой-нибудь точке и перпендикулярна к любой прямой, проведённой в этой плоскости через ту же точку.

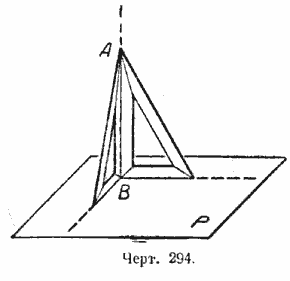
Чтобы провести перпендикуляр к плоскости, берут два чертёжных треугольника и ставят их так, чтобы два катета лежали на плоскости, как показано на чертеже 294, а другую пару катетов совмещают. Эти два катета и образуют перпендикуляр к данной плоскости.

На чертеже 294 прямая АВ перпендикулярна к плоскости Р.

Перпендикулярность прямой АВ к плоскости Р легко проверить: для этого надо взять ещё один чертёжный треугольник и несколько раз в различных положениях приложить его к двум первым треугольникам так, чтобы его катет всякий раз совмещался с катетом АВ. Тогда другой катет третьего треугольника всё время будет находиться в плоскости Р. Значит, можно считать проверенным, что прямая АВ образует прямые углы с любой прямой, проведённой на плоскости через её основание, т. е. является перпендикуляром к плоскости.

Таким образом, мы приходим к выводу: если прямая, пересекающая плоскость в какой-нибудь точке О, перпендикулярна к двум прямым, проведённым на плоскости через точку О, то эта прямая перпендикулярна к плоскости.

Этот вывод является признаком перпендикулярности прямой к плоскости.

Через любую произвольно взятую точку можно провести перпендикуляр к данной плоскости, но только один.

Длина перпендикуляра, опущенного из какой-нибудь точки на плоскость, называется расстоянием от этой точки до плоскости.

5. Площадь поверхности куба.

Чтобы вычислить площадь поверхности куба, достаточно вычислить площадь одной его грани и полученное число помножить на 6. Если ребро куба обозначить через а, то площадь поверхности одной его грани будет равна а 2 , а площадь всей поверхности куба (полная поверхность) составит 6а 2 .

S = 6а 2 , где S — площадь полной поверхности куба.

Площадь поверхности его оснований составит 2а 2 . Площадь поверхности боковых его граней составит 4а 2 .

1. Ребро куба равно 8 см (10 см, 12 см, 20 см). Вычислить площадь всей его поверхности; площадь оснований; площадь его боковой поверхности.

2. Площадь полной поверхности куба равна 150 кв. см (600 кв. см, 216 кв. см, 864 кв. см). Вычислить длину его ребра.

3. Площадь боковой поверхности куба равна 100 кв. см (64 кв. см, 324 кв. см, 576 кв. см). Вычислить площадь его полной поверхности.

4. Сделать из плотной бумаги модель куба, ребро которого равно 8 см.

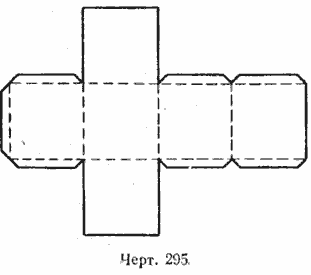
Указание. Для того чтобы полученное геометрическое тело сохраняло свою форму, у развёртки куба необходимо сделать небольшие закраины (черт. 295). Если их подклеить, они составят каркас, который придаст необходимую жёсткость модели.

5. Сколько потребуется белил для окраски с обеих сторон бака (без крышки), имеющего форму куба с ребром в 80 см, если на окраску 1 кв.м требуется белил 0,25 кг?

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

10 класс. Геометрия. Параллельные прямые в пространстве.

10 класс. Геометрия. Параллельные прямые в пространстве.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

1. Тема и цели урока

Мы уже изучали параллельные прямые в планиметрии. Теперь нужно дать определение параллельных прямых в пространстве и доказать соответствующие теоремы.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

2. Определение параллельных прямых в пространстве

Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (Рис. 1.).

Обозначение параллельных прямых: a || b.

Видео:Пересекающиеся прямыеСкачать

3. Теорема 1 и ее доказательство

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Дано: прямая а, (Рис. 2.)

Доказать: существует единственная прямая b || a,

Через прямую а и точку , не лежащую на ней, можно провести единственную плоскость α (Рис. 3.). В плоскости α можно провести единственную прямую b, параллельную а, проходящую через точку M (из аксиомы планиметрии о параллельных прямых). Существование такой прямой доказано.

Докажем единственность такой прямой. Предположим, что существует другая прямая с, проходящая через точку M и параллельная прямой а. Пусть параллельные прямые а и с лежат в плоскости β. Тогда плоскость β проходит через точку M и прямую а. Но через точку M и прямую а проходит единственная плоскость (в силу теоремы 2). Значит, плоскости β и α совпадают. Из аксиомы параллельных прямых, следует, что прямые b и с совпадают, так как в плоскости существует единственная прямая, проходящая через данную точку и параллельная заданной прямой. Единственность доказана.

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

4. Лемма (о двух параллельных прямых, пересекающих плоскость) и ее доказательство

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Дано: а || b,

Доказать:

Доказательство: (Рис. 4.)

Существует некоторая плоскость β, в которой лежат параллельные прямые а и b. Точка М принадлежит и плоскости α, и прямой а, которая лежит в плоскости β. Значит, М – общая точка плоскостей α и β. А по третьей аксиоме, существует прямая MN, по которой пересекаются эти две плоскости.

Прямая MN пересекается с прямой b.(так как в противном случае, получается, что прямые MN и b параллельные, то есть a = MN, что невозможно, так как прямая а пересекается с плоскостью α в точке М по условию). То есть точка N – это точка пересечения прямой b и плоскости α..

Докажем, что N — это единственная общая точка прямой b и плоскости α. Допустим, что есть другая точка, но тогда прямая bпринадлежит плоскости α (по второй аксиоме). То есть MN = b, что невозможно, так как прямые а и bпараллельны, а прямая а должна пересекаться с прямой MN. Лемма доказана.

Видео:Параллельность прямых. 10 класс.Скачать

5. Теорема 2 и ее доказательство

Если две прямые параллельны третьей, то они параллельны.

Дано:

Доказать: .

Доказательство: (Рис. 5.)

Выберем произвольную точку К на прямой b. Тогда существует единственная плоскость α, проходящая черезточку К и прямую а. Докажем, что прямая bлежит в плоскости α.

Предположим противное. Пусть прямая bне лежит в плоскости α. Тогда прямая bпересекает плоскость α в точке К. Так как прямые bи с параллельны, то, согласно лемме, прямая с также пересекает плоскость α. Прямые а и с также параллельны, значит, по лемме, прямая а также пересекает плоскость α, но это невозможно, так как прямая а лежит в плоскости α. Получили противоречие. То есть, предположение было неверным, а значит, прямая bлежит в плоскости α.

Докажем, что прямые а и b не пересекаются. Предположим противное. Пусть прямые а и bпересекаются в некоторой точке М. Но тогда получается, что через точку М проходят две прямые а и b, параллельные прямой с, что невозможно в силу теоремы 1. Получили противоречие. Значит, прямые а и b не пересекаются.

Мы доказали, что прямые а и b не пересекаются и что существует плоскость α, в которой лежат прямые а и b. Значит, прямые а и bпараллельны (по определению), что и требовалось доказать.

Видео:Параллельные прямые. 6 класс.Скачать

6. Итоги урока

Итак, мы дали определение параллельных прямых и доказали теорему о параллельных прямых в пространстве. Также мы доказали важную лемму о пересечении параллельными прямыми плоскости и с помощью этой леммы доказали теорему: если две прямые параллельны третьей, то они параллельны. Эта теория будет использоваться дальше и для доказательства других теорем, и для решения задач.

Видео:Пересекающиеся и параллельные прямые, лучи, отрезки. Задачи. Геометрия. Математика 2 класс.Скачать

Презентация по математике на тему «Параллельность в пространстве»

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

D C A B Параллельные прямые в пространстве

Устная работа. А В С Д А1 В1 С1 Д1 α Дано: куб АВСДА1В1С1Д1 Найдите: Несколько точек, которые лежат в плоскости α; Несколько точек, которые не лежат в плоскости α; Несколько прямых, которые лежат в плоскости α; Несколько прямых, которые не лежат в плоскости α; Несколько прямых которые пересекают прямую ВС; Несколько прямых, которые не пересекают прямую ВС.

Параллельные прямые в пространстве 1 Каково может быть взаимное расположение двух прямых на плоскости? (совпадают, пересекаются, параллельны) 2 Дайте определение параллельных прямых на плоскости. Параллельными называются прямые, не имеющие общих точек. a b a ∩ b

Параллельные прямые в пространстве Параллельными прямыми в пространстве называются прямые, которые лежат в одной плоскости и не пересекаются(не имеют общих точек). Определение ( ) a b a  ,   b a ∩ b

Так как две прямые в пространстве называются параллельными, если они не пересекаются и лежат в одной плоскости. Значит, через две параллельные прямые можно провести плоскость и только одну. a b a ΙΙ b

Теорема о параллельных прямых Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и только одну. Если даны пр. a, M є a , то : 1. через пр. a можно провести пр. b ΙΙ a. 2. пр. b -единственная a β M b

Параллельные прямые в пространстве Дан куб. Являются ли параллельными прямые: D C A B D1 C1 A1 B1 1) АА1 и DD1, АА1 и СС1? Ответ обоснуйте. 2) АА1 и DС? Они пересекаются? В пространстве есть прямые, которые не пересекаются, но и не являются параллельными.

Параллельные прямые в пространстве Две прямые называются скрещивающимися, если они не лежат в одной плоскости и не имеют общих точек.

Признак скрещивающихся прямых Если b є α, a ∩ α = M, M є b, то прямые a и b скрещиваются. a b α M

Найти: 3 пары параллельных прямых, 3 пары скрещивающихся прямых, 3 пары пересекающихся прямых. Пересекаются ли прямые B1D и BC? B1D и A1C1? A B C D A1 B1 C1 D1

Параллельные прямые в пространстве По рисункам назовите: 1) пары скрещивающихся ребер; 2) пары параллельных ребер. D C A B K L N K1 L1 N1

Параллельные прямые в пространстве Алгоритм распознавания взаимного расположения двух прямых в пространстве Лежат ли в одной плоскости? Имеют хотя бы одну общую точку? Имеют более одной общей точки? а и в а = в а  в а в а в Да Да Да Нет Нет Нет .

Лемма Дано: a ΙΙ b, Если a ∩ α, то b∩α a b α β M N

Теорема Если две прямые параллельны третьей прямой, то они параллельны. bιιс , аιιс Значит аιιb Параллельность трех прямых с а b β

Задача. Точки Е,F,M,N – середины рёбер.Установите вид четырёхугольника ЕМNF и найдите его периметр ,еслиDB=12 см , АС=14 см. 12 14 A B C D E F M N

Параллельные прямые в пространстве 1 Всегда ли две непересекающиеся прямые в пространстве параллельны? 2 Какие две прямые в пространстве называются параллельными? 3 4 Сколько можно провести в пространстве прямых, проходящих через данную точку, параллельных данной прямой? Какие прямые называются скрещивающимися?

Параллельность прямой и плоскости в пространстве

Параллельность прямой и плоскости Возможны три случая взаимного расположения прямой и плоскости в пространстве:

1. Если прямая и плоскость имеют одну общую точку, то прямая пересекает эту плоскость.

2. Прямая и плоскость имеют две общие точки.

3. Прямая и плоскость не имеют общих точек.

Определение Прямая и плоскость называются параллельными, если они не имеют общих точек. β а а ∩ β а // β

Признак параллельности двух прямых. Если прямая, лежащая в одной из пересекающихся плоскостей, параллельна другой плоскости, то она параллельна их линии пересечения. Если aєα, allβ, α ∩ β = c, то allc α β a c

Параллельность прямой и плоскости (устно) E и F — середины AD и CD P и K — середины AB и BC Доказать: EF ll (ABC) PK (ADC). A B C D E F K P

Задача Средняя линия трапеции лежит в некоторой плоскости. Докажите, что основания трапеции параллельны данной плоскости. A B C D E F α

ЗАДАЧА Дано: Δ АВС ,АС// α АС = 10 см АВ ∩ α = К ВС ∩ α = D ВК : КА = 2 : 3 Найти: КD

ЗАДАЧА Дано: Δ АВС ,АС//α АС = 10 см АВ ∩ α = К ВС ∩ α = D ВК : КА = 2 : 3 Найти: КD С В К D α А

Признак параллельности двух плоскостей. Пусть даны пл-ти α и β, a ∩ b, a1∩b1, a , b є α, a1 , b1 є β, Если а// a1 ; b // b1 ,то α II β Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то плоскости параллельны. a b α b1 a1 β

Свойства.__________ 1. Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны. Если α II β, γ ∩ α = a, γ ∩ β = b, то a II b α β γ a b

2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. Если α II β, AD II BC, то AD = BC α β А B C D

Задача. 5 4 3 6 ? ? . . * * » » a b O α β A B A1 B1

ЗАДАЧА Дано: ∆ АВС ; α // β АВ ∩ α=D;АВ ∩ β=Е ВС ∩ α=К;ВС ∩ β=Р ВD:ВЕ=2:3 ВК=4см Найти: ВР и ВЕ

ЗАДАЧА А В С D Е К Р α β Дано: ∆ АВС ; α // β АВ ∩ α=D;АВ ∩ β=Е ВС ∩ α=К;ВС ∩ β=Р ВD:ВЕ=2:3 ВК=4см Найти: ВР и ВЕ 4

Используемая литература: 1. Геометрия: Учебник для средней школы. 10–11 классы./ Под ред. Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др. – М.: Просвещение, 1992. 2. Геометрия. 10 класс. Поурочные планы / Авт.-сост. Г.И. Ковалева – Волгоград: Учитель, 2004 Презентацию подготовила: Седова Оксана Михайловна преподаватель математики ГАОУ МО СПО «Печенгский политехнический техникум» 2016 год Параллельные прямые в пространстве

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 953 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 330 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Седова Оксана МихайловнаНаписать 2308 22.12.2016

Номер материала: ДБ-044801

22.12.2016 239

22.12.2016 568

22.12.2016 361

22.12.2016 1706

22.12.2016 3707

22.12.2016 727

22.12.2016 509

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учительница из Киргизии победила в конкурсе Минпросвещения РФ «Учитель-международник»

Время чтения: 2 минуты

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📸 Видео

Взаимное расположение прямых в пространстве. 10 класс.Скачать

10 класс - Геометрия - Скрещивающиеся прямыеСкачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Плоскость. Пересекающиеся прямые. 6 класс.Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

7 класс, 24 урок, Определение параллельных прямыхСкачать

6 класс, 44 урок, Параллельные прямыеСкачать

Параллельные прямые (задачи).Скачать

Скрещивающиеся прямыеСкачать