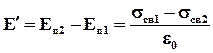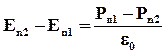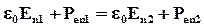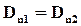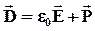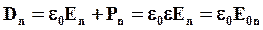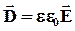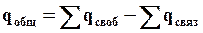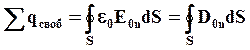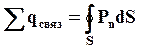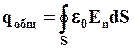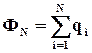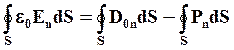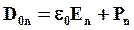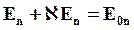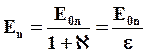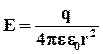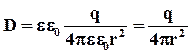На границе раздела двух диэлектриков с различными диэлектрическими проницаемостями выполняются два следующих условия:
1) равны тангенциальные составляющие напряженности поля:
2) равны нормальные составляющие электрической индукции:
Индекс 1 относится к первому диэлектрику, индекс 2 — ко второму.
Первое условие вытекает из того, что в потенциальном поле fyEdl = 0 по любому замкнутому контуру; второе представляет следствие теоремы Гаусса.
Докажем справедливость первого условия. С этой целью выделим плоский замкнутый контур mnpqm (рис. 19.11) и составим вдоль него циркуляцию вектора напряженности электрического поля. Верхняя сторона контура расположена в диэлектрике с диэлектрической проницаемостью е2, нижняя — в диэлектрике с е,. Длину стороны тп, равную длине стороны pq, обозначим dl. Контур возьмем так, что размеры пр и qm будут бесконечно малы по сравнению с dl. Поэтому составляющими интеграла dl вдоль вертикальных сторон в силу их малости пренебрежем. Составляющая §Ё dl на пути тп равна Ё2 dl2 = E2l dl, по пути pq равна Ё dlx = -Еи dl. Знак минус появился потому, что элемент длины на пути pq и касательная составляющая вектора Ёх направлены в противоположные стороны (cosl80° = -1). Таким образом, §Ё dl = E2ldl-Eu dl = 0 или Еи=Е2г
Убедимся в справедливости второго условия. С этой целью на границе раздела двух сред выделим очень малых размеров параллелепипед (рис. 19.12). Внутри выделенного объема есть связанные заряды и нет свободных (случай наличия свободных зарядов на границе раздела рассмотрим отдельно), поэтому ?/3 dS = 0.
Поток вектора D:
т. e. при наличии на границе раздела двух сред свободных зарядов нормальная составляющая вектора D скачком изменяется на значение плотности свободных зарядов на границе раздела.
Из § 19.3 известно, что потенциалу придается смысл работы при переносе единичного заряда. При переходе через границу, отделяющую один диэлектрик от другого, например, при переходе от точки п к точке р на рис. 19.11, нормальная составляющая напряженности является величиной конечной, а длина пути стремится к нулю. Произведение их равно нулю.
Поэтому при переходе через границу раздела двух диэлектриков потенциал не претерпевает скачков.
Видео:Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Вектор электрического смещения. Граница двух диэлектриков
Источником электростатического поля являются свободные и связанные электрические заряды: линии напряженности начинаются на положительных зарядах (или в бесконечности) и оканчиваются на отрицательных (или в бесконечности).
Однако при решении задач, связанных с электрическим полем в диэлектрике, в ряде случае оказывается более удобным учитывать только поле свободных зарядов. Для этого вводится понятие вектора электрического смещения ( 
Рассмотрим изменение электрического поля на достаточно протяженной границе двух однородных и однородно поляризованных диэлектриков 1 и 2.
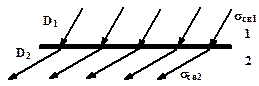 | В первом диэлектрике напряженность электрического поля и вектор поляризации соответственно равны 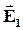 и и 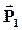 , во втором диэлектрике — , во втором диэлектрике — 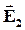 и и 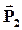 . . |
В общем случае все эти четыре вектора произвольно ориентированы в диэлектриках, поэтому можно говорить об их тангенциальных к границе раздела (Et1, Et2 и Pt1, Pt2) и нормальных (En1, En2 и Pn1, Pn2) составляющих.
На границе возникнут связанные электрические заряды противоположных знаков, поверхностные плотности которых равны sсв1 и sсв2. Эти заряды создадут электрическое полеE’. Напряженность E’ уменьшит нормальную составляющую напряженности в одном диэлектрике и увеличит в другом, поэтому E’будет определятьсяразностью нормальных составляющих напряженности:
Это уравнение можно записать так:
Отсюда видно, что на границе двух диэлектриков сохраняется нормальная составляющая:
Это и есть вектор электрического смещения.
Т.е. можно говорить о линиях электрического смещения и о потоке вектора электрического смещения через некоторую поверхность.
Поток вектора электрического смещения не изменятся на границе двух диэлектриков, т.е. линии этого вектора не начинаются и не заканчиваются на связанных зарядах, а линии напряженности поля начинаются и заканчиваются на связанных зарядах.
Из приведенных соотношений видно,
Внутри диэлектрика 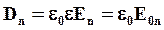
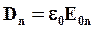
Видно, что величина Dn остается постоянной при переходе из вакуума в среду, а величина En изменяется.
Или в векторной форме:
Запишем для нашего случая теорему Гаусса. Общий заряд в диэлектрике qобщ можно найти как разность свободных зарядов и связанных зарядов.
Сумма 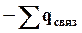
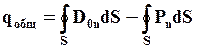
отсюда получаем:
Величина поля внутри диэлектрика:
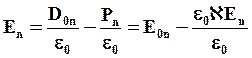
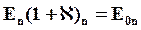
В других конкретных случаях соотношения для электростатического поля с диэлектриком имеют другой вид и чаще всего значительно более сложный, нежели полученные нами для плоской пластины внутри конденсатора. В частности, в некоторых случаях введение диэлектрика сопровождается не только ослаблением поля, но и его усилением.
 | Поле, созданное зарядом q в т. A и B, по направлению совпадает с полем связанных зарядов диэлектрика M, внесенного в поле заряда q. |
В т. C величины E0 и E’ направлены в противоположные стороны, т.е. в этой точке внесение диэлектрика сопровождается ослаблением поля.
Напряженность электрического поля точечного заряда q в диэлектрике выражается формулой:
Получаем выражение для электрического смещения поля точечного заряда:
Как видно, электрическое смещение в однородном изотропном диэлектрике не зависит от свойств вещества.
Видео:46. Граничные условия для электрического поляСкачать

Граничные условия для векторов электрического и магнитного поля на границе раздела двух сред
А) Граничные условия для вектора электрической индукции.
Рассмотрим границу раздела двух сред с различными диэлектрическими проницаемостями 

 |
Рис.1.4.1.Элементарный цилиндр, выделенный на границе раздела двух сред для определения граничных условий на вектор электрической индукции. 

Согласно теореме Гаусса-Остроградского поток вектора электрической индукции 

Устремим высоту цилиндра к нулю 

Где 

Введем поверхностную плотность заряда:

Размерность поверхностной плотности заряда 
Тогда (3.1.2) можно переписать в виде

Если плотность поверхностного заряда равна нулю (

Мы можем сформулировать следующее важное утверждение:
На границе раздела, не содержащей поверхностных зарядов, нормальная составляющая вектора электрической индукции непрерывна.
Б) Граничные условия для вектора магнитной индукции.
Рассмотрим границу раздела двух сред, обладающих различной магнитной проницаемостью. Из тех же соображений, что и в предыдущем пункте и принимая во внимание, что магнитных зарядов не существует, можно записать

Это равенство равносильно следующему утверждению:
На границе раздела двух сред нормальная составляющая вектора магнитной индукции всегда непрерывна.
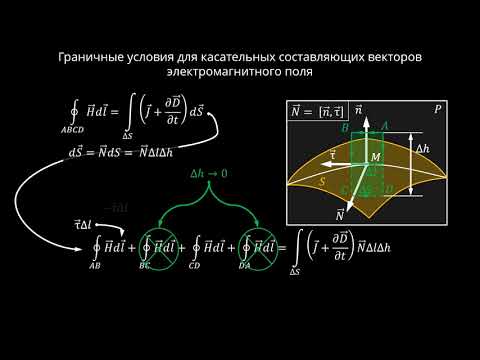
В) Граничные условия для вектора напряженности электрического поля 
Рассмотрим снова границу раздела двух сред с различными диэлектрическими проницаемостями 

Где L — выбранный контур, L = 2 (1 + 
 |
Рис.3.1.2. Контур на границе раздела двух сред, используемый при определении граничных условий для векторов напряженности электрического поля.
Устремим ширину контура 


Откуда следует, что

Это равенство равносильно следующему утверждению:
На границе раздела двух сред касательная составляющая вектора напряженности электрического поля всегда непрерывна.
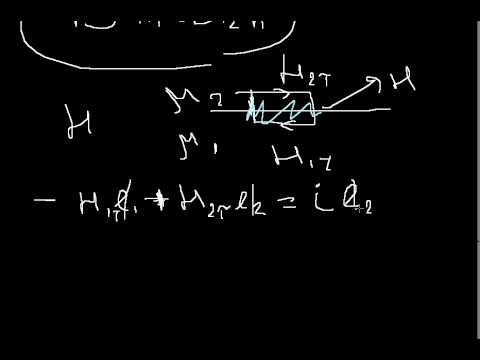
Г) Граничные условия для вектора напряженности магнитного поля Н.
Как в предыдущем случае выделим на границе раздела двух сред замкнутый контур L (рис.1.4.2). Воспользуемся законом полного тока

Где 
Учтем, что вдоль границы раздела может течь ток проводимости, тогда при стремлении 

Размерность поверхностной плотности тока [
Откуда следует, что

Это равенство равносильно следующему утверждению:
На границе раздела двух сред разность касательных составляющих напряженности магнитного поля равна поверхностной плотности тока.
При отсутствии поверхностного тока

Это равенство равносильно следующему утверждению:
На границе раздела двух сред, по которой не течет поверхностный ток, касательная составляющая магнитного поля непрерывна.
Д) Граничные условия на поверхности идеального проводника.
Определим идеальный проводник, как проводник, внутрь которого не может проникать электромагнитное поле 




Силовые линии электрического поля перпендикулярны к поверхности идеального проводника; силовые линии магнитного поля касательны к поверхности идеального проводника, как показано на рис.3.1.3.
 |
Рис.3.1.3. Силовые линии электрического и магнитного полей вблизи поверхности идеального проводника.
💥 Видео
Лекция 4-2. Условия на границе раздела двух диэлектриковСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

2.5 Граничные условия для векторов поля на поверхности раздела средСкачать
Билет №06-08 "Диэлектрики"Скачать

44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

поле Е на границе раздела диэлектриковСкачать

ЧК_МИФ (ЛИКБЕЗ) 3_2_1 ПРОХОЖДЕНИЕ СВЕТА ЧЕРЕЗ ГРАНИЦУ РАЗДЕЛА ДВУХ СРЕД -1 (Минимум теории)Скачать

Диэлектрики в электрическом поле. 10 класс.Скачать

магнитная защита. Векторы B и H на границе разделаСкачать
Электростатическая индукцияСкачать

Поляризация диэлектрикаСкачать

6 Граничные условия для векторов E и DСкачать

Билеты №18 и 19 "Теорема о циркуляции магнитного поля. Граничные условия"Скачать

45. Электрическое смещениеСкачать

Лекция по физике №12. Электрическое поле в веществе. Проводники и диэлектрики. Вектор индукции.Скачать

Урок 228. Диэлектрики в электрическом поле. Диэлектрическая проницаемостьСкачать

Билет №02 "Теорема Гаусса"Скачать

Лекция 4 -1 Поляризация диэлектриковСкачать