Вектор или скаляр сила тяжести

Пугающие школьника два слова — вектор и скаляр — на самом деле не являются страшными. Если подойти к теме с интересом, то все можно понять. В данной статье рассмотрим, какая величина является векторной, а какая скалярной. Точнее, приведем примеры. Каждый ученик, наверное, обращал внимание, что в физике некоторые величины обозначаются не только символом, но и стрелкой сверху. Что они обозначают? Об этом будет сказано ниже. Постараемся разобраться, чем отличается векторная величина от скалярной.

Видео:Скалярные и векторные величины, основные определения.Скачать

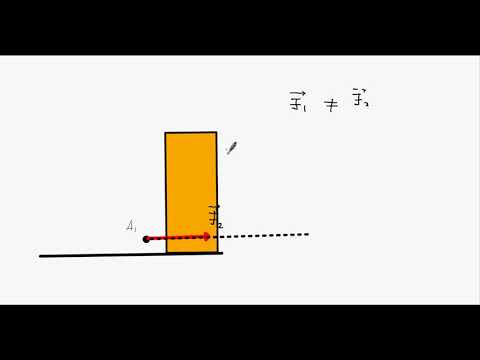
Примеры векторов. Как они обозначаются

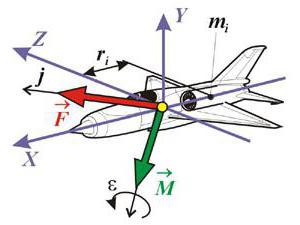
Что подразумевается под вектором? То, что характеризует движение. Не важно, в пространстве или на плоскости. Какая величина является векторной вообще? Например, летит самолет с определенной скоростью на какой-то высоте, имеет конкретную массу, начал движение из аэропорта с нужным ускорением. Что относится к движению самолета? Что заставило его лететь? Конечно, ускорение, скорость. Векторные величины из курса физики являются наглядными примерами. Говоря прямо, векторная величина связана с движением, перемещением.

Вода тоже движется с определенной скоростью с высоты горы. Видите? Движение осуществляется за счет не объема или массы, а именно скорости. Теннисист дает возможность мячику двигаться при помощи ракетки. Он задает ускорение. К слову сказать, приложенная в данном случае сила также является векторной величиной. Потому что она получается вследствие заданных скоростей и ускорений. Сила способна также меняться, осуществлять конкретные действия. Ветер, который колышет листья на деревьях, тоже можно считать примером. Так как имеется скорость.

Видео:Физика 7 класс (Урок№12 - Сила. Сила тяжести.)Скачать

Положительные и отрицательные величины

Векторной величиной называется величина, которая имеет направление в окружающем пространстве и модуль. Снова появилось пугающее слово, на этот раз модуль. Представьте, что нужно решить задачку, где будет фиксироваться отрицательное значение ускорения. В природе отрицательных значений, казалось бы, не существует. Как скорость может быть отрицательной?

У вектора есть такое понятие. Это касается, например, сил, которые приложены к телу, но имеют разные направления. Вспомните третий закон Ньютона, где действие равно противодействию. Ребята перетягивают канат. Одна команда в синих футболках, вторая — в желтых. Вторые оказываются сильнее. Допустим, что вектор их силы направлен положительно. В то же время у первых не получается натянуть канат, но пытаются. Возникает противодействующая сила.

Видео:Физика | Ликбез по векторамСкачать

Векторная или скалярная величина?

Поговорим о том, чем отличается векторная величина от скалярной. Какой параметр не имеет никакого направления, но имеет свое значение? Перечислим некоторые скалярные величины ниже:

• время (секунда, минута, день, год);
• масса (грамм, килограмм, тонна);
• длина, расстояние (сантиметр, метр, километр);
• площадь и объем (метр квадратный и кубический);
• температура (градус Цельсия, Фаренгейт);
• доза радиации, излучения (бар, рентген);
• уровень шума, вибрации (децибел).

Имеют ли все они направление? Нет. Какая величина является векторной, а какая скалярной, можно показать только наглядными примерами. В физике есть такие понятия не только в разделе «Механика, динамика и кинематика», а так же в параграфе «Электричество и магнетизм». Сила Лоренца, индукция, магнитное поле — все это так же векторные величины.

Видео:Урок 116. Работа силы тяжести. Потенциальная энергия тела, поднятого над ЗемлейСкачать

Вектор и скаляр в формулах

В учебниках по физике часто встречаются формулы, в которых есть стрелочка сверху. Вспомните второй закон Ньютона. Сила («F» со стрелочкой сверху) равна произведению массы («m») и ускорения («a» со стрелочкой сверху). Как говорилось выше, сила и ускорение являются величинами векторными, а вот масса — скалярной.

К сожалению, не во всех изданиях есть обозначение этих величин. Наверное, сделано это для упрощения, чтобы школьников не вводить в заблуждение. Лучше всего покупать те книги и справочники, в которых обозначены векторы в формулах.

То, какая величина является векторной, покажет иллюстрация. Рекомендуется обращать внимание на картинки и схемы на уроках физики. Векторные величины имеют направление. Куда направлена сила тяжести? Конечно же, вниз. Значит, стрелочка будет показана в том же направлении.

В технических вузах изучают физику углубленно. В рамках многих дисциплин преподаватели рассказывают о том, какие величины являются скалярными и векторными. Такие знания требуются в сферах: строительство, транспорт, естественные науки.

Видео:СИЛА ТЯЖЕСТИ масса ВЕС ТЕЛА 7 класс физика ПерышкинСкачать

Сила тяжести, масса и вес тела, невесомость

Видео:Урок 62. Сила тяжести и вес тела. Невесомость.Скачать

Масса

Масса обозначается символом (m ), является скалярной величиной и в СИ измеряется в килограммах.

Иногда массу в условии некоторых задач задают в граммах или, например, в тоннах. Чтобы перевести массу в килограммы, используют такие формулы:

[ large boxed < beginm = left( text right) cdot 10^ left( textright) \ m = left( text right) cdot 10^ left( textright) \ m = left( text right) cdot 10^ left( textright) \ m = left( text right) cdot 10^ left( textright) \ end> ]

• ( large text ) – подставьте количество тонн вместо этой скобки;
• ( large text ) – вместо этой скобки подставьте количество сотен килограммов;
• ( large text ) – подставьте количество граммов вместо этой скобки;
• ( large text ) – вместо этой скобки подставьте количество миллиграммов;

От массы зависят инерционные и гравитационные свойства физических тел.

Масса в природе проявляет себя двумя способами. Поэтому, выделяют:

1. массу инертную и
2. массу гравитационную.

Инертная масса

Масса инертная влияет на способность тела двигаться по инерции. Такая масса используется в формуле второго закона Ньютона.

Пусть два тела находятся в инерциальной системе отсчета. Если какая-либо сила одинаково ускоряет эти тела, то они обладают одинаковой инертной массой. Здесь «одинаково ускоряет» следует понимать, как «сообщает одинаковые ускорения».

Гравитационная масса

Гравитационная масса определяет силу, с которой тело притягивается к другим телам. Эта масса используется в формуле закона всемирного тяготения.

Различные эксперименты показали, что инертная и гравитационная массы равны с высокой степенью точности. Поэтому, при изучении школьной физики можно просто говорить «масса», не уточняя, о какой именно массе идет речь.

Так же, масса входит в формулы для расчета импульса и механической энергии.

Массой обладают все макроскопические тела, а, так же, такие элементарные частицы, как протоны, нейтроны, электроны и т. д. Однако, существуют и частицы, у которых нет массы покоя, например – фотоны.

Примечание: Фотон – элементарная частица, переносчик электромагнитного взаимодействия, движется со скоростью света, часто проявляет волновые свойства. Подробнее о фотонах вы узнаете в основах квантовой физики.

Видео:Сила. Единицы силыСкачать

Сила тяжести

Сила тяжести — это сила, с которой Земля притягивает к себе тело.

(large vec<F_<text>> left(Hright) ) — сила тяжести, она действует на тело со стороны планеты (или другого крупного небесного тела, например, астероида, или звезды).

(large m left(textright) ) — масса тела;

(large vec left(frac<text><c^>right) ) — ускорение свободного падения, это не постоянная величина, она может меняться. Читайте подробнее о ускорении свободного падения .

Вес – это сила. Этой силой тело давит на опору, когда опирается на нее, или растягивает подвес, когда на нем висит.

Является векторной величиной и обозначается символом (vec

).

(vec

left(Hright) ) – вес тела, как любая сила в СИ измеряется в Ньютонах.

Вес отличается от массы. Вес, как и любая сила, измеряется в Ньютонах, а масса измеряется в килограммах.

Когда тело опирается о горизонтальную поверхность, его вес равен по модулю силе реакции опоры по третьему закону Ньютона. Поэтому, в задачах для нахождения веса удобно вычислять силу (large vec). Как только мы найдем реакцию опоры (large vec), мы найдем вес тела, давящего на эту опору.

Примечание: Векторы равны по модулю, когда обладают одинаковыми длинами. Так как длина вектора обозначается числом, то физики о равных по модулю векторах сил могут сказать: силы численно равны.

Чем вес отличается от силы тяжести

Вес — это сила, принадлежащая телу. А сила тяжести — это сила, действующая на тело со стороны планеты, или любого другого (крупного) тела.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Что такое невесомость

Подбросим мяч вверх и рассмотрим свободный полет мяча. Пока он в полете, он не давит на опору и не растягивает подвес. Проще говоря, мяч находится в невесомости – то есть, не имеет веса.

Масса есть всегда, а вес может отсутствовать! Как убедимся чуть позже, одна и та же масса может обладать различным весом.

Видео:Работа силы тяжести. Работа силы упругости. Потенциальная энергия | Физика 10 класс #20 | ИнфоурокСкачать

Как изменяется вес тела лифте

Давайте выясним, какой вес имеет тело, находящееся в покоящемся лифте, или в лифте, который будет двигаться вверх или вниз с ускорением, или без него.

Если скорость лифта не изменяется

Сначала рассмотрим покоящийся лифт (рис. 1а), либо движущийся вверх (рис. 1б), или вниз (рис. 1в) с неизменной скоростью.

Примечание: «неизменной», также, значит «постоянной», или «одной и той же».

По первому закону Ньютона, когда действие других тел скомпенсировано, тело, не меняющее свою скорость, находится в инерциальной системе отсчета.

Как видно из рисунка, взаимодействуют два объекта: тело и опора. Тело давит своим весом на опору, а опора отвечает телу (рис. 1) силой своей реакции.

Будем записывать для рассмотренных случаев рисунка 1 векторные силовые уравнения:

[ large N – m cdot g = 0 ]

А в этой статье подробно и с объяснениями написано о том, как составлять силовые уравнения (ссылка).

Прибавив к обеим частям уравнения величину ( m cdot vec ), получим

[ large N = m cdot g ]

По третьему закону Ньютона, вес тела и реакция опоры направлены противоположно и равны по модулю. Поэтому, найдя силу реакции опоры, мы автоматически находим вес тела.

Воспользуемся тем, что ( left|vec right|= left|vec

right|), получим

То есть, вес тела в покоящемся лифте, или движущемся вверх или вниз с неизменной скоростью, будет равен ( mg ). Если вектор скорости лифта не изменяется ни по направлению, ни по модулю, лифт можно считать инерциальной системой отсчета.

Если скорость лифта изменяется

Теперь выясним, каким весом будет обладать тело в лифте, движущемся с ускорением (рис. 2).

Примечание: Лифт, движущийся с ускорением, не является инерциальной системой отсчета. Читайте подробнее о инерциальных системах.

Запишем силовые уравнения. Для рисунка 2а, уравнение выглядит так:

[ large N – m cdot g = m cdot a ]

А для рисунка 2б, так:

[ large N – m cdot g = — m cdot a ]

Прибавим теперь к обеим частям уравнений величину ( m cdot g ), получим:

( large N = m cdot a + m cdot g ) – для случая рис. 2а;

( large N = — m cdot a + m cdot g ) – для рис. 2б;

Вынесем массу за скобки

( large N = m cdot left( a + g right) ) – для рис. 2а;

( large N = m cdot left( -a + g right) ) – для рис. 2б;

Учтем, что ( left|vec right|= left|vec

right|), окончательно запишем

Для рисунка 2а — движение лифта вверх с ускорением:

Вес тела в движущемся с ускорением вверх лифте, будет равен ( m cdot left( g + a right) ), то есть, превышает величину ( m cdot g ).

Когда лифт движется вниз с ускорением (рис. 2б), вес тела, наоборот — уменьшается:

Напомним, что вес в покоящемся, или движущемся вверх или вниз с неизменной скоростью лифте, в точности равен ( m cdot g ).

Вес тела в движущемся вниз с ускорением лифте, равен ( m cdot left( g — a right) ), это меньше величины ( m cdot g ).

Значит, одна и та же масса может обладать разным весом, мало того, в некоторых случаях вес вообще может отсутствовать. Масса есть всегда, а вес может отсутствовать!

Видео:Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

Что такое перегрузка

Когда вес тела больше силы тяжести, говорят, что возникает перегрузка.

[ large boxed

m cdot g >]

Когда говорят о перегрузке, принято сравнивать ускорение движения вверх с ускорением свободного падения (large vec).

Например, при движении ракеты с ускорением вверх, космонавт может испытывать перегрузки до 7g. Это значит, что его вес увеличивается в 7 раз.

Первый космонавт мира — Юрий Гагарин, упоминал о перегрузке: «…какая-то сила вдавливает меня в кресло все больше и больше. … трудно пошевелить рукой или ногой…».

Подобным образом мы испытываем перегрузки в самолете во время взлета — эти перегрузки вдавливают нас в кресло. Правда, эти перегрузки значительно меньше, чем перегрузки летчиков — спортсменов, или военных, летчиков — космонавтов. Представители этих профессий тренируют свое тело для того, чтобы перегрузки легче переносить.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Подведем итоги

(P = m cdot g ) — вес тела в покоящемся или движущемся вверх или вниз с постоянной скоростью лифте.

( P = m cdot left( g + a right) ) — вес, когда лифт движется с ускорением вверх;

( P = m cdot left( g — a right) ) — вес в движущемся вниз с ускорением;

Если ускорение лифта при его движении вниз ( a = g ), наступит невесомость, вес тела исчезнет ( P = 0 ).

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вектор или скаляр сила тяжести

В физике существуют скалярные величины (скаляры) и векторные величины (векторы). Хотя, правильнее в последнем случае все-таки говорить векторная величина, часто говорят, например, «вектор скорости».

Упрощенно можно сказать, что скаляр — это просто число.

Векторная величина — это когда есть число, которое имеет еще и направление в пространстве. Вектор в трехмерном пространстве можно представить в виде тройки чисел, каждое из которых есть компонента вектора относительно соответствующей координаты в трехмерной системе координат.

Чтобы совсем запутаться, рекомендую обратиться к Википедии: https://ru.wikipedia.org/wiki/Векторная_величина.

Для тех, кто любит попроще — первый том Фейнмановских лекций по физике.

Для нас важно понять два момента:

1) Примерами скаляров являются: длина, площадь, время, масса, плотность, температура и т.п.

Для наших задач достаточно понимания скаляра, как величины (числа с размерностью) без направления.

2) Под вектором мы будем понимать направленный отрезок. То есть три числа (мы ведь живем в трехмерном пространстве), которые преобразуются по определенным правилам при переходе от одной системы координат к другой.

Попробуем обойтись без математических формул этих правил. Просто представим в нашем трехмерном пространстве направленный отрезок. Некую стрелку, которая, для простоты, неподвижна, неизменна, и имеет направление от одного конца к другому. Или даже представим, что у нас есть определенная операция перемещения в пространстве. У нее есть величина (расстояние перемещения по прямой из начальной точки в конечную) и направление.

И представим систему координат (например, прямоугольную), которая неподвижна относительно нас, и начало отсчета которой совпадает с началом нашего направленного отрезка.

Отлично! Тогда координаты «заостренного» конца нашего «направленного» отрезка с началом в точке (0,0,0) в этой системе координат будут выражаться тремя числами (А_х, А_y, А_z). Будет ли эта тройка чисел вектором?

Будет! Мы же сами задали эти три числа, как координаты вектора .

Теперь мы берем и поворачиваем произвольно нашу систему координат (но пока не сдвигаем начало координат). Тогда в новой системе координат координаты нашего вектора будут (А_x’, А_y’, А_z’). Заметьте, сам наш вектор (направленный отрезок в трехмерном пространстве) не изменился. Как бы мы не вращали систему координат, тройка чисел будет меняться, но вектор (в смысле направленного отрезка) останется на своем месте. Он смотрит в одну и ту же «точку вселенной». О как! И длина его не меняется из-за вращения системы координат.

А теперь вывод. То, что важно для физики!

Если у нас есть три какие-то величины (возможно, мы даже не знаем, связаны ли они между собой), которые изменяются с изменением системы координат, по такому же закону, по которому изменяются компоненты вектора из предыдущего абзаца ((А_х, А_y, А_z) —> (А_x’, А_y’, А_z’)), то мы можем смело утверждать, что эти три величины представляют собой компоненты какого-то вектора.

Формулы можно посмотреть у Фейнмана или еще где-нибудь. Они пока для понимания не столь важны. А важно следующее!

Рассмотрим подробнее физические величины в нашем трехмерном пространстве. Зададим прямоугольную систему координат X , Y , Z . Помним, что у нас есть еще время t.

Теперь посмотрим, что есть что.

Путь вектор или скаляр? Скаляр. Почему?

Перемещение — вектор. У перемещения есть начало и конец, есть величина перемещения и направление перемещения. Таким образом, у него три компоненты — три величины, по одной на каждую из координат.

Далее сами перебираем физические величины и определяем, что есть скаляр, а что вектор!

📺 Видео

Урок 8. Векторные величины. Действия над векторами.Скачать

Введение в векторы и скаляры (видео 1)| Векторы. Прямолинейное движение | ФизикаСкачать

2.1. Скалярные и векторные физические величиныСкачать

Физика.7 класс. Скалярные и векторные физические величины /11.09.2020/Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Движение тела под действием силы тяжести. 1 часть. 9 класс.Скачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Основы кинематики. Тема 2. Скалярные и векторные величины. Действия над векторамиСкачать