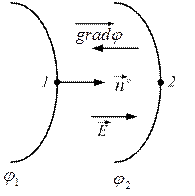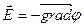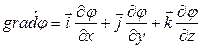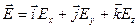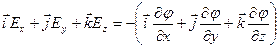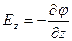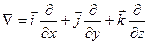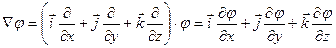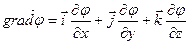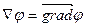Вектор градиента потенциала электростатического поля (5 видео)

Вектор градиента потенциала электростатического поля

§7 Работа силы электростатического поля при перемещении заряда.

Потенциальный характер сил поля.

Циркуляция вектора напряженности

Рассмотрим электростатическое поле, создаваемое зарядом q . Пусть в нем перемещается пробный заряд q ₀ . В любой точке поля на заряд q ₀ действует сила

де — модуль силы, — орт радиус-вектора , определяющего положение заряда q ₀ относительно заряда q . Так как сила меняется от точки к точке, то работу силы электростатического поля запишем как работу переменной силы:

Ввиду того, что рассматривали перемещение заряда из точки 1 в точку 2 по произвольной траектории, можно сделать вывод, что работа по перемещению точечного заряда в электростатическом поле не зависит от формы пути, а определяется лишь начальным и конечным положением заряда. Это свидетельствует о том, что электростатическое поле является потенциальным, а сила Кулона – консервативной силой. Работа по перемещению заряда в таком поле по замкнутому пути всегда рвана нулю.

— проекция на направление контура ?.

Учтем, что работа по замкнутому пути равно нулю

— ЦИРКУЛЯЦИЯ вектора напряженности.

Циркуляция вектора напряженности электростатического поля, взятая по произвольному замкнутому контуру всегда равна нулю.

§7 Потенциал.

Связь между напряженностью и потенциалом.

Градиент потенциала.

Эквипотенциальные поверхности

Поскольку электростатическое поле является потенциальным работа по перемещению заряда в таком поле может быть представлена, как разность потенциальных энергий заряда в начальной и конечной точках пути. (Работа равна уменьшению потенциальной энергии, или изменению потенциальной энергии, взятому со знаком минус.)

Постоянную определяют из условия, что при удалении заряда q ₀ на бесконечность его потенциальная энергия должна быть равна нулю.

Различные пробные заряды q ₀ _i , помещенные в данную точку поля будут обладать в этой точке различными потенциальными энергиями:

…

Отношение W _пот _i к величине пробного заряда q ₀ _i , помещенного в данную точку поля является величиной постоянной для данной точки поля для всех пробных зарядов. Это отношение называется ПОТЕНЦИАЛОМ.

ПОТЕНЦИАЛ – энергетическая характеристика электрического поля. ПОТЕНЦИАЛ численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

Работу по перемещению заряда можно представить в виде

Потенциал измеряется в Вольтах

ЭКВИПОТЕНЦИАЛЬНЫМИ ПОВЕРХНОСТЯМИ называются поверхности равного потенциала (φ = const ). Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Связь между напряженностью и потенциалом φ можно найти, исходя из того, что работу по перемещению заряда q на элементарном отрезке d ? можно представить как

С другой стороны

— градиент потенциала.

Напряженность поля равна градиенту потенциала, взятому со знаком минус.

Градиент потенциала показывает, как меняется потенциал на единицу длины. Градиент перпендикулярен функции и направлен в сторону возрастания функции. Следовательно, вектор напряженности перпендикулярен эквипотенциальной поверхности и направлен в сторону убывания потенциала.

Рассмотрим поле, создаваемое системой N точечных зарядов q ₁ , q ₂ , … q_N . Расстояния от зарядов до данной точки поля равны r ₁ , r ₂ , … r_N . Работа, совершаемая силами этого поля над зарядом q ₀ , будет равна алгебраической сумме работ сил, каждого заряда в отдельности.

гле

Потенциал поля, создаваемого системой зарядов, определяется как алгебраическая сумма потенциалов, создаваемых в этой же точке каждым зарядом в отдельности.

§9 Вычисление разности потенциалов плоскости, двух плоскостей, сферы, шара, цилиндра

Используя связь между φ и определим разность потенциалов между двумя произвольными точками

Вектор градиента потенциала электростатического поля

Разность потенциалов поля равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ.

2. Разность потенциалов поля двух бесконечных параллельных разноименно заряженных плоскостей с поверхностной плотностью заряда σ.

Если х₁ = 0; х₂ = d , то или

3. Разность потенциалов поля равномерно заряженной сферической поверхности радиуса R .

Внутри сферической поверхности потенциал всюду одинаков и равен

4. Разность потенциалов поля объемно заряженного шара радиуса R с общим зарядом Q.

Вне шара r ₁ , r ₂ > R ,

Внутри шара

5. Разность потенциалов поля равномерно заряженного цилиндра (или бесконечно длинной нити).

r > R :

Содержание

Градиент потенциала
Градиент потенциальных характеристик, как его рассчитать и пример
черты
Как рассчитать?
пример
осуществление
Шаг 1
Шаг 2
Шаг 3
📹 Видео

Видео:Потенциал электрического поля. 10 класс.Скачать

Градиент потенциала

Градиент потенциала – это скорость возрастания потенциала в направлении кротчайшем между двумя точками.

Между двумя точками имеется некоторая разность потенциалов. Если эту разность разделить на кратчайшее расстояние между взятыми точками, то полученное значение будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками.

Градиент потенциала показывает направление наибольшего возрастания потенциала, численно равен модулю напряженности и отрицательно направлен по отношению к нему.

В определении градиента существенны два положения:

1) Направление, в котором берутся две близлежащие точки, должно быть таким, чтобы скорость изменения была максимальной.

2) Направление таково, что скалярная функция в этом направлении возрастает.

Для декартовой системы координат:

Скорость изменения потенциала в направлении оси Х, Y, Z:

; ;

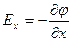
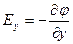
Два вектора равны только тогда, когда равны друг другу их проекции. Проекция вектора напряженности на ось Х равна проекции скорости изменения потенциала вдоль оси Х, взятой с обратным знаком. Аналогично для осей Y и Z.

; ; .

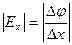
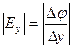
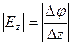
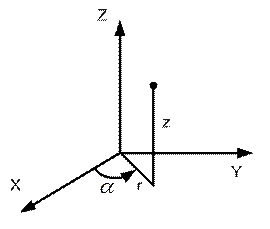
В цилиндрической системе координат выражение градиента потенциала будет иметь следующий вид:

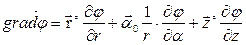
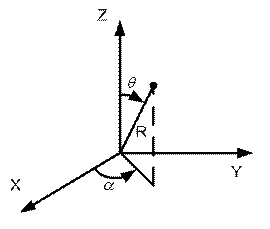
А в сферической системе координат:

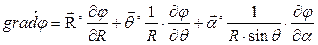
Дифференциальный оператор Гамильтона (оператор Набла)

Для сокращения записи операций над скалярными и векторными величинами употребляют дифференциальный оператор Гамильтона или оператор Набла:

Под дифференциальным оператором Гамильтона понимают сумму частных производных по 3-м координатным осям, умноженных на соответствующие единичные векторы (орты).

Применим оператор Гамильтона к потенциалу:

Правые части одинаковы, значит, будут одинаковы и левые части:

Оператор Гамильтона сочетает в себе как векторные, так и скалярные свойства и может быть применен к скалярным и векторным функциям.

Дата добавления: 2015-07-30 ; просмотров: 19610 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:27 [Полярная звезда] Градиент потенциалаСкачать

Градиент потенциальных характеристик, как его рассчитать и пример

градиент потенциала является вектором, который представляет отношение изменения электрического потенциала по отношению к расстоянию в каждой оси декартовой системы координат. Таким образом, вектор градиента потенциала указывает направление, в котором скорость изменения электрического потенциала больше, в зависимости от расстояния.

В свою очередь, модуль градиента потенциала отражает скорость изменения электрического потенциала в определенном направлении. Если значение этого известно в каждой точке пространственной области, то электрическое поле может быть получено из градиента потенциала.

Электрическое поле определяется как вектор, с которым оно имеет определенное направление и величину. Определяя направление, в котором электрический потенциал уменьшается быстрее, удаляясь от контрольной точки, и деля это значение на пройденное расстояние, получается величина электрического поля..

1 Характеристики
2 Как рассчитать?
3 Пример
- 3.1 Упражнение
4 Ссылки

Видео:Физика 10 класс (Урок№27 - Напряжённость и потенциал электростатического поля.Разность потенциалов.)Скачать

черты

Градиент потенциала представляет собой вектор, ограниченный конкретными пространственными координатами, который измеряет отношение изменения между электрическим потенциалом и расстоянием, пройденным этим потенциалом.

Наиболее выдающиеся характеристики градиента электрического потенциала подробно описаны ниже:

1- Потенциальный градиент — это вектор. Следовательно, он имеет определенную величину и направление.

2- Поскольку потенциальный градиент является вектором в пространстве, он имеет величины, адресованные по осям X (ширина), Y (высокая) и Z (глубина), если в качестве эталонной системы координат берется декартова система координат.

3- Этот вектор перпендикулярен эквипотенциальной поверхности в точке, в которой оценивается электрический потенциал.

4- Вектор градиента потенциала направлен в направлении максимального изменения функции электрического потенциала в любой точке..

5- Модуль градиента потенциала равен модулю, полученному из функции электрического потенциала по отношению к расстоянию, пройденному в направлении каждой из осей декартовой системы координат..

6- Потенциальный градиент имеет нулевое значение в стационарных точках (максимальная, минимальная и седловая точки).

7- В международной системе единиц (СИ) единицами измерения градиента потенциала являются вольт / метры.

8. Направление электрического поля такое же, в котором электрический потенциал уменьшает свою величину быстрее. В свою очередь, градиент потенциала указывает в направлении, в котором потенциал увеличивает свое значение по отношению к изменению положения. Тогда электрическое поле имеет то же значение градиента потенциала, но с противоположным знаком.

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Как рассчитать?

Разность электрических потенциалов между двумя точками (точка 1 и точка 2) определяется следующим выражением:

V1: электрический потенциал в точке 1.

V2: электрический потенциал в точке 2.

E: величина электрического поля.

Ѳ: угол наклона вектора электрического поля, измеренного относительно системы координат.

Выражая указанную формулу дифференциальным способом, получаем следующее:

Коэффициент E * cos (Ѳ) относится к модулю компонента электрического поля в направлении dl. Пусть L — горизонтальная ось плоскости отсчета, тогда cos (Ѳ) = 1, вот так:

Далее, отношение между изменением электрического потенциала (dV) и изменением пройденного расстояния (ds) является модулем градиента потенциала для упомянутого компонента.

Из этого следует, что величина градиента электрического потенциала равна компоненте электрического поля в направлении исследования, но с противоположным знаком.

Однако, поскольку реальная среда является трехмерной, градиент потенциала в данной точке должен быть выражен как сумма трех пространственных компонентов на осях X, Y и Z декартовой системы..

Разбивая вектор электрического поля на три прямоугольных компонента, мы получаем следующее:

Если в плоскости имеется область, в которой электрический потенциал имеет одинаковое значение, частная производная этого параметра по каждой из декартовых координат будет равна нулю.

Таким образом, в точках, которые находятся на эквипотенциальных поверхностях, напряженность электрического поля будет иметь нулевую величину.

Наконец, вектор градиента потенциала может быть определен как точно такой же вектор электрического поля (по величине) с противоположным знаком. Таким образом, мы имеем следующее:

Видео:ГрадиентСкачать

пример

Из приведенных выше расчетов необходимо:

Теперь, прежде чем определять электрическое поле как функцию градиента потенциала или наоборот, сначала необходимо определить направление, в котором разность электрических потенциалов растет..

После этого определяется коэффициент изменения электрического потенциала и изменения пройденного расстояния..

Таким образом, мы получаем величину соответствующего электрического поля, которая равна величине градиента потенциала в этой координате.

осуществление

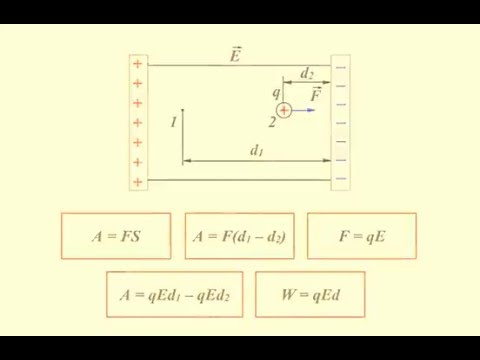
Есть две параллельные пластины, как показано на следующем рисунке.

Шаг 1

Направление роста электрического поля на декартовой системе координат определяется.

Электрическое поле растет только в горизонтальном направлении, учитывая расположение параллельных пластин. Следовательно, можно сделать вывод, что компоненты градиента потенциала на оси Y и оси Z равны нулю..

Шаг 2

Данные, представляющие интерес различаются.

— Разность потенциалов: dV = V2 — V1 = 90 В — 0 В => dV = 90 В.

— Разница в расстоянии: дх = 10 сантиметров.

Чтобы обеспечить соответствие единиц измерения, используемых в соответствии с Международной системой единиц, величины, не выраженные в СИ, должны быть соответственно преобразованы. Таким образом, 10 сантиметров равны 0,1 метра, и, наконец, dx = 0,1 м.