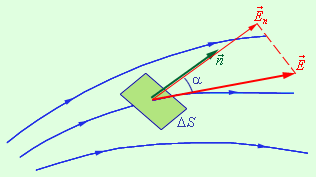
Вектор ds в физике (7 видео) | Курс школьной геометрии

Вектор ds в физике

Поток вектора напряженности электрического поля. Пусть небольшую площадку D S (рис.1.2) пересекают силовые линии электрического поля, направление которых составляет с нормалью n к этой площадке угол a . Полагая, что вектор напряженности Е не меняется в пределах площадки D S, определим поток вектора напряженности через площадку D S как

Поскольку густота силовых линий равна численному значению напряжённости E, то количество силовых линий, пересекающих площадку D S , будет численно равно значению потока D F _E через поверхность D S . Представим правую часть выражения (1.3) как скалярное произведение векторов E и D S = n D S , где n – единичный вектор нормали к поверхности D S . Для элементарной площадки d S выражение (1.3) принимает вид

Через всю площадку S поток вектора напряженности вычисляется как интеграл по поверхности

Поток вектора электрической индукции. Поток вектора электрической индукции определяется аналогично потоку вектора напряженности электрического поля

В определениях потоков заметна некоторая неоднозначность, связанная с тем, что для каждой поверхности можно задать две нормали противоположного направления. Для замкнутой поверхности положительной считается внешняя нормаль.

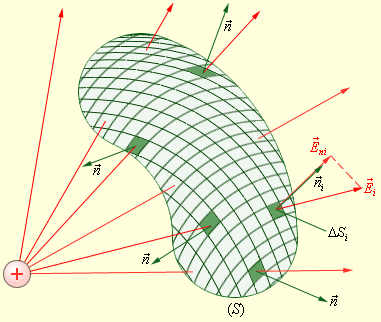
Теорема Гаусса. Рассмотрим точечный положительный электрический заряд q , находящийся внутри произвольной замкнутой поверхности S (рис. 1.3). Поток вектора индукции через элемент поверхности d S равен
(1.4)

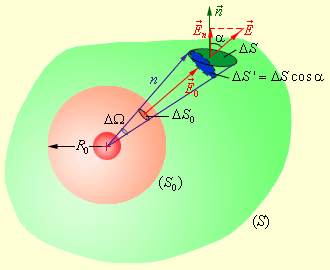
Составляющую d S_D = d S cos a элемента поверхности d S в направлении вектора индукции D рассматриваем как элемент сферической поверхности радиуса r, в центре которой расположен заряд q .

Учитывая, что d S_D / r 2 равен элементарному телесному углу d w , под которым из точки нахождения заряда q виден элемент поверхности d S, преобразуем выражение (1.4) к виду d F _D = q d w / 4 p , откуда после интегрирования по всему окружающему заряд пространству, т. е. в пределах телесного угла от 0 до 4 p , получим

Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен заряду, заключенному внутри этой поверхности.

Если произвольная замкнутая поверхность S не охватывает точечный заряд q (рис. 1.4), то, построив коническую поверхность с вершиной в точке нахождения заряда, разделим поверхность S на две части: S₁ и S₂. Поток вектора D через поверхность S найдем как алгебраическую сумму потоков через поверхности S₁ и S₂:

Обе поверхности из точки нахождения заряда q видны под одним телесным углом w . Поэтому потоки равны

Поскольку при вычислении потока через замкнутую поверхность используется внешняя нормаль к поверхности, легко видеть, что поток Ф _1D _2D > 0. Суммарный поток Ф _D = 0. Это означает, что поток вектора электрической индукции через замкнутую поверхность произвольной формы не зависит от зарядов, расположенных вне этой поверхности.

Если электрическое поле создаётся системой точечных зарядов q ₁, q ₂, ¼ , q_n , которая охватывается замкнутой поверхностью S, то, в соответствии с принципом суперпозиции, поток вектора индукции через эту поверхность определяется как сумма потоков, создаваемых каждым из зарядов. Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью:

(1.5)

Следует отметить, что заряды q_i не обязательно должны быть точечными, необходимое условие — заряженная область должна полностью охватываться поверхностью. Если в пространстве, ограниченном замкнутой поверхностью S, электрический заряд распределен непрерывно, то следует считать, что каждый элементарный объём d V имеет заряд . В этом случае в правой части выражения (1.5) алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S:

(1.6)

Выражение (1.6) является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности. Теорему Гаусса можно записать и для потока вектора напряженности электрического поля :

Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность. Еще раз подчеркнем, что, несмотря на то, что напряжённость электрического поля E и электрическая индукция D зависят от расположения в пространстве всех зарядов, потоки этих векторов через произвольную замкнутую поверхность S определяются только теми зарядами, которые расположены внутри поверхности S.

Дифференциальная форма теоремы Гаусса. Отметим, что интегральная форма теоремы Гаусса характеризует соотношения между источниками электрического поля (зарядами) и характеристиками электрического поля (напряженностью или индукцией) в объеме V произвольной, но достаточной для формирования интегральных соотношений, величины. Производя деление объема V на малые объемы V_i , получим выражение

справедливое как в целом, так и для каждого слагаемого. Преобразуем полученное выражение следующим образом:

(1.7)

и рассмотрим предел, к которому стремится выражение в правой части равенства, заключенное в фигурных скобках, при неограниченном делении объема V. В математике этот предел называют дивергенцией вектора (в данном случае вектора электрической индукции D):

Дивергенция вектора D в декартовых координатах:

Таким образом выражение (1.7) преобразуется к виду:

Учитывая, что при неограниченном делении сумма в левой части последнего выражения переходит в объемный интеграл, получим

Полученное соотношение должно выполняться для любого произвольно выбранного объема V . Это возможно лишь в том случае, если значения подынтегральных функций в каждой точке пространства одинаковы. Следовательно, дивергенция вектора D связана с плотностью заряда в той же точке равенством

или для вектора напряженности электростатического поля

Эти равенства выражают теорему Гаусса в дифференциальной форме.

Отметим, что в процессе перехода к дифференциальной форме теоремы Гаусса получается соотношение, которое имеет общий характер:

Выражение называется формулой Гаусса — Остроградского и связывает интеграл по объему от дивергенции вектора с потоком этого вектора сквозь замкнутую поверхность, ограничивающую объем.

1) В чем заключается физический смысл теоремы Гаусса для электростатического поля в вакууме

2) В центре куба находится точечный заряд q . Чему равен поток вектора Е:

а) через полную поверхность куба; б) через одну из граней куба.

Изменятся ли ответы, если:

а) заряд находится не в центре куба, но внутри его ; б) заряд находится вне куба.

3) Что такое линейная, поверхностная, объемная плотности заряда.

4) Укажите связь объемной и поверхностной плотности зарядов.

5) Может ли поле вне разноименно и однородно заряженных параллельных бесконечных плоскостей быть отличным от нуля

6) Электрический диполь помещен внутрь замкнутой поверхности. Каков поток сквозь эту поверхность

Содержание

Теорема Гаусса для электростатического поля. Поток и дивергенция вектора Е
Теорема Гаусса
Поток вектора напряженности
Теорема Гаусса. Доказательство
Применение теоремы Гаусса
📹 Видео

Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Теорема Гаусса для электростатического поля. Поток и дивергенция вектора Е

Рис. 12.3. Однородное поле Ё изображено параллельными силовыми линиями. Штриховыми линиями изображена проекция площади ДS на плоскость, перпендикулярную силовым линиям поля

Рис. 12.4. К определению потока напряженности через неплоекую поверхность 5, когда поле Е неоднородно

Рассмотрим элементарную площадку dS, которую пронизывают линии напряженности (рис. 12.3). Пусть п — единичный вектор, перпендикулярный площадке AS и направленный под углом а к вектору Ё. Тогда число линий напряженности, пронизывающих элементарную площадку AS, равно Е AS cosa = E_nAS, где Е_п — проекция вектора Ё на нормаль п к площадке dS.

Величина ДФ_Е = ?„AS = Е AS cosa = — Ё AS называется потоком вектора напряженности электростатического поля через площадку AS. Здесь AS = AS п — вектор, модуль которого равен AS; его направление совпадает с направлением п к площадке. Отметим, что выбор направления вектора И условен: его можно было направить в противоположную сторону (рис. 12.3).

Если поле неоднородно и поверхность S неплоская (рис. 12.4), то, разбивая поверхность на участки АД,- (/ = 1, п) так, чтобы каждый элемент AS,- был плоским и электрическое поле в пределах элемента было однородным, для потока напряженности через всю поверхность получаем

где E_t — напряженность поля, отвечающая векторному элементу площади поверхности Д5). При Д5,-—»0 сумма переходит в интеграл по всей поверхности и равенство становится точным:

Поток вектора Е через произвольную замкнутую поверхность S, т.е. через поверхность, ограничивающую некоторую область пространства, определяется по формуле

где знак ф показывает, что интеграл берется по замкнутой поверхности. s

Для наглядного изображения электростатического поля через единичную площадку, перпендикулярную силовым линиям поля, будем проводить силовые линии N_E, число которых равно модулю потока Ф_? вектора напряженности.

Рис. 12.5. К выбору вектора dS = dSn элемента замкнутой поверхности S

В случае замкнутой поверхности S принято брать нормаль п , внешнюю по отношению к области, охватываемой этой поверхностью, т.е. внешнюю нормаль (рис. 12.5). Знак потока Ф_? определяется следующим образом. Если силовые линии выходят из объема (рис. 12.5, угол а я/2 , т.е. cosa г

Рис. 12.6. К выводу теоремы Гаусса

Рассмотрим воображаемую замкнутую сферическую поверхность S радиуса г, в центре которой помещен точечный положительный заряд q. Силовые линии заряда q центрально-симметричны (рис. 12.6). В соответствии с формулой (12.11а) в каждой точке этой поверхности проекция вектора Е на внешнюю нормаль

Следовательно, поток вектора Е через поверхность S

Выражение (12.116) не зависит от /*. Так как силовые линии нигде не пересекаются, то их число будет таким же через любую замкнутую поверхность, охватывающую заряд q.

Если заряд положителен, то на нем начинается число линий

Для отрицательного заряда линии идут из бесконечности, заканчиваясь на нем:

Количество линий при этом N_E K >0, т.е. неотрицательно, так как q Теорема Гаусса для вектора Е в дифференциальной форме. При рассмотрении поля, создаваемого макроскопическим зарядом, заряд считают распределенным в пространстве непрерывно с конечной объемной плотностью р. Тогда можно считать, что каждый элементарный объем AV представляет собой точечный заряд pAV.

Разделим поток вектора Е через замкнутую поверхность S на объем AV, ограниченный данной поверхностью:

и будем стягивать эту поверхность в точку. Полученная скалярная величина называется дивергенцией вектора Е:

Можно показать, что в декартовой системе координат

Согласно теореме Остроградского из векторного анализа

Сопоставив уравнения (12.11) и (12.12), сформулируем теорему Гаусса (12.11) в дифференциальной форме: дивергенция вектора Е в некоторой точке электростатического поля равна объемной плотности электрического заряда р в этой точке, деленной на ?₀:

Те точки поля, где div? положительна, называются источниками векторного поля (положительные заряды), а те точки, где она отрицательна, — стоками (отрицательные заряды).

Видео:Физика | Ликбез по векторамСкачать

Теорема Гаусса

Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.

Видео:Вектор в Физике. Как Рисовать Вектор? Модуль Вектора || Урок Физики 8 класс // Подготовка к ЕГЭСкачать

Поток вектора напряженности

Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка Δ S .

Элементарный поток вектора напряженности (через площадку S ) – это физическая величина, равная произведению модуля вектора E → , площади Δ S и косинуса угла α между вектором и нормалью к площадке:

Δ Φ = E Δ S cos α = E n Δ S.

В данной формуле E n является модулем нормальной составляющей поля E → .

Рисунок 1 . 3 . 1 . Иллюстрация элементарного потока Δ Φ .

Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S . Разобьем заданную поверхность на площадки небольшого размера Δ S i , рассчитаем элементарные потоки Δ Φ i поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис. 1 . 3 . 2 ):

Φ = ∑ ∆ Φ i = ∑ E m ∆ S i

Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.

Рисунок 1 . 3 . 2 . Расчет потока Ф через произвольную замкнутую поверхность S .

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Теорема Гаусса. Доказательство

Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.

Поток вектора напряженности электростатического поля E → через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε 0 .

Уравнение Гаусса имеет вид:

Φ = 1 ε 0 ∑ q в н у т р

Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) S . В центре заданной поверхности расположен точечный заряд q . Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:

E = E n = 1 4 π ε 0 · q R 2 ,

где R является радиусом сферы.

Поток Φ через поверхность шара запишется, как произведение E и площади сферы 4 π R 2 . Тогда: Φ = 1 ε 0 q .

Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью S замкнутого типа; зададим также вспомогательную сферу R 0 (рис. 1 . 3 . 3 ).

Рисунок 1 . 3 . 3 . Поток электрического поля точечного заряда через произвольную поверхность S , окружающую заряд.

Возьмем для рассмотрения конус с малым телесным углом Δ Ω при вершине. Рассматриваемый конус задаст на сфере малую площадку Δ S 0 , а на поверхности S – площадку Δ S . Элементарные потоки Δ Φ 0 и Δ Φ через эти площадки являются одинаковыми. В самом деле:

Δ Φ 0 = E 0 Δ S 0 , Δ Φ = E Δ S cos α = E Δ S ‘ ,

где выражением Δ S ‘ = Δ S cos α определяется площадка, которая задастся конусом с телесным углом Δ Ω на поверхности сферы радиуса n .

Поскольку ∆ S 0 ∆ S ‘ = R 0 2 r 2 , то ∆ Φ 0 = ∆ Φ . Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ 0 через поверхность вспомогательной сферы:

Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q , поток Φ равен нулю. Этот случай проиллюстрирован на рис. 1 . 3 . 2 . Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.

Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S сложится из потоков Φ i электрических полей отдельных зарядов. Когда заряд q i расположен внутри поверхности S , он дает вклад в поток, равный q i ε 0 . В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.

Так, мы доказали теорему Гаусса.

Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.

Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Применение теоремы Гаусса

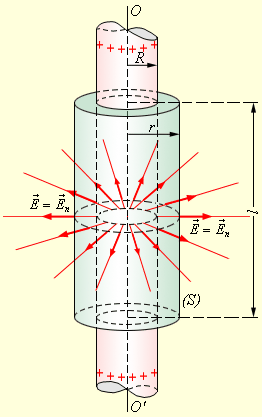
В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R . Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l , закрытого с обоих торцов (рис. 1 . 3 . 4 ).

Рисунок 1 . 3 . 4 . Иллюстрация поля однородно заряженного цилиндра. O O ‘ – ось симметрии.

Если r ≥ R , то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2 π r l . Применим закон Гаусса и получим:

Φ = E 2 π r l = τ l ε 0 .

В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:

Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.

Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r R . В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ = E 2 π r l . Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.

Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.

К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).

При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.

Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. 1 . 3 . 5 ).

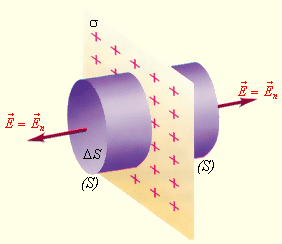
Рисунок 1 . 3 . 5 . Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.

Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:

2 E ∆ S = σ ∆ S ε 0 или E = σ 2 ε 0 .

Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.

Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.