В выпуклом четырехугольнике abcd отрезки соединяющие середины противоположных сторон пересекаются 60

Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Ваш ответ

Видео:№101. Докажите, что отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаютсяСкачать

решение вопроса

Видео:№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,712
• разное 16,823

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Планиметрия с нуля и до уровня ЕГЭ 2023 за 4 часа | Вся теория по №1,16 | Математика профильСкачать

В выпуклом четырехугольнике отрезки, соединяющие середины противоположных сторон, равны соответственно x и y и пересекаются под углом 60?

Геометрия | 10 — 11 классы

В выпуклом четырехугольнике отрезки, соединяющие середины противоположных сторон, равны соответственно x и y и пересекаются под углом 60.

Найдите диагонали четырехугольника.

Смотри вложение : * Если картинка обрывается, уменьшить экран надо [ctrl — (минус)] или скачать.

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

В выпуклом четырехугольнике проведем два отрезка, соединяющие середины противоположных сторон?

В выпуклом четырехугольнике проведем два отрезка, соединяющие середины противоположных сторон.

Докажите, что эти отрезки пересекают друг друга в середине.

Видео:ЕГЭ Математика 16 Задание Планиметрическая задача Четырехугольники Середины сторонСкачать

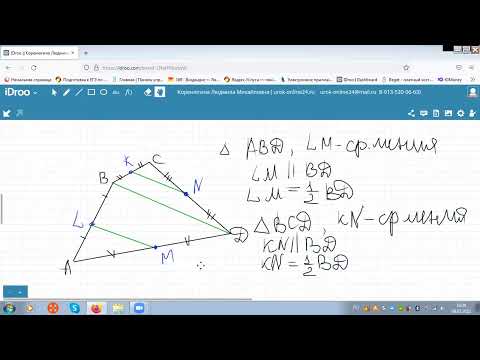
В выпуклом четырехугольнике KLMN длина отрезка, соединяющего середины диагоналей KM и LN, равна одному метру?

В выпуклом четырехугольнике KLMN длина отрезка, соединяющего середины диагоналей KM и LN, равна одному метру.

Прямые LN и KN перпендикулярны.

Найдите длину отрезка, соединяющего середины сторон KL и MN.

Видео:Как решать С4, геометрия. Урок 12. #ЕГЭ по математике 2014. Середины противоположных сторонСкачать

В выпуклом четырехугольнике KLMN длина отрезка, соединяющего середины диагоналей KM и LN равна 1 м?

В выпуклом четырехугольнике KLMN длина отрезка, соединяющего середины диагоналей KM и LN равна 1 м.

ML перепендикулярна KN.

Найти длину отрезка, соединяющего середину сторон KL и MN.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Диагонали четырехугольника равны 16 см и 20 см и пересекаются под углом в 30°?

Диагонали четырехугольника равны 16 см и 20 см и пересекаются под углом в 30°.

Найдите площадь этого четырехугольника.

Видео:Планиметрия_03_05Скачать

Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, взаимно перпендикулярны и равны 2 и 7?

Отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, взаимно перпендикулярны и равны 2 и 7.

Найти площадь четырехугольника.

Видео:Планиметрия_03_02Скачать

Диагонали ромба равны 13 и 29 см?

Диагонали ромба равны 13 и 29 см.

Найдите периметр четырехугольника, образованного отрезками, соединяющего последовательно середины сторон ромба.

Видео:8 класс, 4 урок, ПараллелограммСкачать

Середина стороны ab выпуклого четырехугольника abcd равноудалена от всех его вершин?

Середина стороны ab выпуклого четырехугольника abcd равноудалена от всех его вершин.

Найдите ab если cd = 3 а углы c и d этого четырёхугольника равны 116градусов и 109градусов соответственно.

Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

Периметр ромба АВСD равен 14?

Периметр ромба АВСD равен 14.

Стороны четырехугольника А1В1С1D1 соединяют середины сторон ромба.

Найдите периметр четырехугольника А2В2С2D2 стороны которого соединяют середины сторон четырехугольника А1В1С1D1.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ЧЕРТЕЖ?

Докажите, что если у двух выпуклых четырехугольников соответственно равны все стороны и по одному углу между соответствующими сторонами, то такие четырехугольники равны.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вершины четырехугольника ABCD являются серединами сторон четырехугольника, диагонали которого равны 6 дм и пересекаются под углом 60°?

Вершины четырехугольника ABCD являются серединами сторон четырехугольника, диагонали которого равны 6 дм и пересекаются под углом 60°.

Вычислите площадь четырехугольника ABCD.

Желательно приложить рисунок.

Вопрос В выпуклом четырехугольнике отрезки, соединяющие середины противоположных сторон, равны соответственно x и y и пересекаются под углом 60?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 10 — 11 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Ну так — с. 1) Центр вписанной окружности – точка пересечения биссектрис треугольника, то есть АО и ОС – это биссектрисы 2) Блин, я в тупике, прости Надеюсь, первый пункт тебе поможет❤️((((.

A(1 ; 1 ; 5) ; b(2 ; — 4 ; 6) ; c( — 5 ; 3 ; 1) 1) Скалярное произведение векторов. 2a — 2c = (2 ; 2 ; 10) — ( — 10 ; 6 ; 2) = (2 + 10 ; 2 — 6 ; 10 — 2) = (12 ; — 4 ; 8) b + 3a = (2 ; — 4 ; 6) + (3 ; 3 ; 15) = (2 + 3 ; — 4 + 3 ; 6 + 15) = (5 ; — 1 ;..

Сумма всех углов треугольника 180, значит один внешний будет 260 — 180 = 80. Тогда смежный с ним внутренний угол равен 180 — 80 = 100 Значит, что этот внутренний угол — это угол вершины равнобедренного треугольника, так как он не может быть углом пр..

Видео:Геометрия 8 класс за 1 час | Математика | УмскулСкачать

В выпуклом четырёхугольнике середины противоположных сторон соединены отрезками, причём один из них делит этот четырёхугольник на две равновеликие фигуры, а другой делит площадь в отношении 9:13

В выпуклом четырёхугольнике середины противоположных сторон соединены отрезками, причём один из них делит этот четырёхугольник на две равновеликие фигуры, а другой делит площадь в отношении $9:13$. а) Доказать, что данный четырёхугольник является трапецией. б) Найти отношение меньшего основания этой трапеции к большему.

а) Рассмотрим выпуклый четырёхугольник $QMNP$ (см. рис.). Пусть $E$ — середина $MQ$, $F$ — середина $NP$, причём $S_=S_$.

Проведём отрезки $EN$ и $EP$. Заметим, что
$S_= / EF⋅ FNsin ∠ EFN= / EF⋅ FP sin ∠ EFP=S_$, так как $NF=FP$ и $sin ∠ EFN=sin (180°-∠ EFN)=sin ∠ EFP$. Отсюда $S_=S_$ ($S_=S_-S_$, $S_=S_-S_$). Опустим в $▵ MNE$ высоту $NN_1$, в $▵ EPQ$ — высоту $PP_1$. Получим: $ / ME⋅ NN_1= / EQ⋅ PP_1$. Но $ME=EQ$, следовательно, $NN_1=PP_1$. Но тогда в четырёхугольнике $N_1NPP_1$ $∠ NN_1P_1=∠ N_1P_1P=90°$, $NN_1=PP_1$, то есть $N_1NPP_1$ — прямоугольник. Значит, $N_1P_1∥ NP$, $MQ∥ NP$. Из предположения о том, что $MN∥ QP$, следует, что отрезок, соединяющий середины сторон $MN$ и $QP$, делит параллелограмм $MNPQ$ на две равновеликие фигуры. Но по условию это не так. Значит, $MN ∦ QP$. Следовательно, $MNPQ$ — трапеция. б) По условию второй отрезок $AB$ делит четырёхугольник так, что площадь $ANPB$ относится к площади $ABQM$ как $9:13$ (см. рис.).

$S_:S_=9:13$. $AB$ — средняя линия трапеции, $AB= / $. $S_= / ⋅ h_1$; $S_= / ⋅ h_2$, где $h_1$ — высота трапеции $ANPB$; $h_2$ — высота трапеции $ABQM$. Так как $NP∥ MQ$, а $AB$ — средняя линия и $AB∥ NP$ и $AB∥ MQ$, то расстояния от $AB$ до $NP$ и от $AB$ до $MQ$ равны, то есть $h_1=h_2$. Отсюда, $<S_> / <S_>= </ > / </ >= <NP+/ > / </ +MQ>= / $, $ / = / $, $39NP+13MQ=27MQ+9NP$, $30NP=14MQ$, $ / = / = / $.

💡 Видео

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Геометрия Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можноСкачать

§-2 № 1-64 - Геометрия 9 класс Мерзляк углубленный уровеньСкачать

#58. Олимпиадная задача о четырехугольникеСкачать

Решение планиметрических задач повышенного уровня сложности Параллелограмм Средняя линияСкачать