Знание — сила. Познавательная информация
Видео:Построение сечения параллельно прямойСкачать

Как построить сечение пирамиды
Разберем, как построить сечение пирамиды, на конкретных примерах. Поскольку в пирамиде нет параллельных плоскостей, построение линии пересечения (следа) секущей плоскости с плоскостью грани чаще всего предполагает проведение прямой через две точки, лежащие в плоскости этой грани.
В простейших задачах требуется построить сечение пирамиды плоскостью, проходящей через данные точки, уже лежащие в одной грани.
Построить сечение плоскостью (MNP)
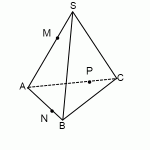
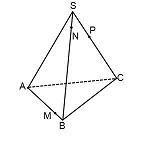
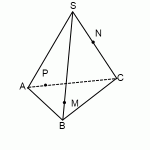
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Треугольник MNP — сечение пирамиды
Точки M и N лежат в одной плоскости ABS, следовательно, через них можем провести прямую. След этой прямой — отрезок MN. Он видимый, значит, соединяем M и N сплошной линией.
Точки M и P лежат в одной плоскости ACS, поэтому через них проведем прямую. След — отрезок MP. Мы его не видим, поэтому отрезок MP проводим штрихом. Аналогично строим след PN.
Треугольник MNP — искомое сечение.
Если точка, через которую требуется провести сечение, лежит не на ребре, а на грани, то она не будет концом следа-отрезка.
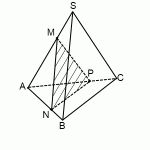
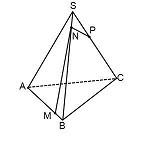
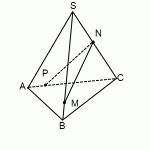
Пример. Построить сечение пирамиды плоскостью, проходящей через точки B, M и N, где точки M и N принадлежат, соответственно, граням ABS и BCS.
Здесь точки B и M лежат в одной грани ABS, поэтому можем через них провести прямую.
Аналогично проводим прямую через точки B и P. Получили, соответственно, следы BK и BL.
Точки K и L лежат в одной грани ACS, поэтому через них можем провести прямую. Ее след — отрезок KL.
Треугольник BKL — искомое сечение.
Однако не всегда через данные в условии точки удается провести прямую. В этом случае нужно найти точку, лежащую на прямой пересечения плоскостей, содержащих грани.
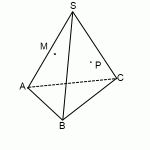
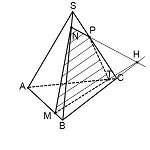
Пример. Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Точки M и N лежат в одной плоскость ABS, поэтому через них можно провести прямую. Получаем след MN. Аналогично — NP. Оба следа видимые, поэтому соединяем их сплошной линией.
Точки M и P лежат в разных плоскостях. Поэтому соединить их прямой не можем.
Продолжим прямую NP.
Она лежит в плоскости грани BCS. NP пересекается только с прямыми, лежащими в этой же плоскости. Таких прямых у нас три: BS, CS и BC. С прямыми BS и CS уже есть точки пересечения — это как раз N и P. Значит, ищем пересечение NP с прямой BC.
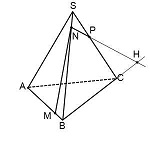
Эта точка H принадлежит как плоскости (BCS), поскольку лежит на прямой NP, так и плоскости (ABC), поскольку лежит на прямой BC.
Таким образом мы получили еще одну точку секущей плоскости, лежащей в плоскости (ABC).
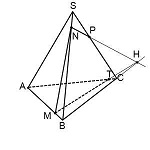
Получим след MT.
T — точка пересечения прямых MH и AC.
Так как T принадлежит прямой AC, то через нее и точку P можем провести прямую, так как они обе лежат в одной плоскости (ACS).
4-угольник MNPT — искомое сечение пирамиды плоскостью, проходящей через данные точки M,N,P.
Мы работали с прямой NP, продлевая ее для отыскания точки пересечения секущей плоскости с плоскостью (ABC). Если работать с прямой MN, приходим к тому же результату.
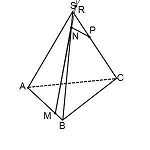
Значит, продлевая MN, ищем точку пересечения ее с прямой AS. Назовем эту точку R.
Точка R лежит на прямой AS, значит, она лежит и в плоскости (ACS), 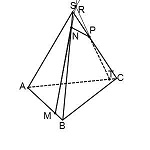
Поскольку точка P лежит в плоскости (ACS), через R и P можем провести прямую. Получаем след PT.
Точка T лежит в плоскости (ABC), поэтому через нее и точку M можем провести прямую.
Таким образом, получили все то же сечение MNPT.
Рассмотрим еще один пример такого рода.
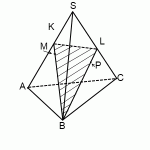
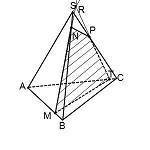
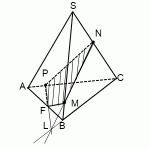
Построить сечение пирамиды плоскостью, проходящей через точки M, N, P.
Через точки M и N, лежащие в одной плоскости (BCS), проводим прямую. Получаем след MN (видимый).
Через точки N и P, лежащие в одной плоскости (ACS), проводим прямую. Получаем след PN (невидимый).
Через точки M и P прямую провести не можем.
1) Прямая MN лежит в плоскости (BCS), где есть еще три прямые: BC, SC и SB. С прямыми SB и SC уже есть точки пересечения: M и N. Поэтому ищем точку пересечения MN с BC. Продолжив эти прямые, получаем точку L.
Точка L принадлежит прямой BC, а значит, она лежит в плоскости (ABC). Поэтому через L и P, которая также лежит в плоскости (ABC) можем провести прямую. Ее след — PF.
F лежит на прямой AB, а значит, и в плоскости (ABS). Поэтому через F и точку M, которая также лежит в плоскости (ABS), проводим прямую. Ее след — FM. Четырехугольник MNPF — искомое сечение.
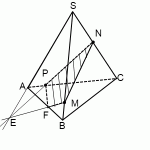
2) Другой путь — продолжить прямую PN. Она лежит в плоскости (ACS) и пересекается с прямыми AC и CS, лежащими в этой плоскости, в точках P и N.
Значит, ищем точку пересечения PN с третьей прямой этой плоскости — с AS. Продолжаем AS и PN, на пересечении получаем точку E. Поскольку точка E лежит на прямой AS, принадлежащей плоскости (ABS), то через E и точку M, которая также лежит в (ABS), можем провести прямую. Ее след — FM. Точки P и F лежат водной плоскости (ABC), проводим через них прямую и получаем след PF (невидимый).
Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Решение задач на применение аксиом и их следствий (в пирамиде)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы решим несколько задач с помощью трех аксиом и двух теорем-следствий в пирамиде.
В начале урока мы повторим аксиомы, вспомним, что такое треугольная пирамида, и повторим теоремы-следствия из аксиом. Далее мы решим несколько задач на взаимное расположение точек, прямых и плоскостей в треугольной пирамиде, опираясь на повторенный теоретический материал.
Видео:Как строить сечения тетраэдра и пирамидыСкачать

Задание №14 на ЕГЭ-2019. Различные методы и способы решения.
Видео:Построение сечения пирамиды по трем точкамСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Задание №14 на ЕГЭ-2019. Различные методы и способы решения. Колупаев В.А. МБОУ СОШ №25.
Задание № 14 на ЕГЭ-2019. Различные методы и способы решения.
№ 1.1.(а) В правильной треугольной пирамиде SABC точка P — делит сторону AB в отношении 2:3, считая от вершины A , точка K — делит сторону BC в отношении 2:3, считая от вершины C . Через точки P и K параллельно SB проведена плоскость .
а) Докажите, что сечение пирамиды плоскостью является прямоугольником.
б) Найдите расстояние от точки S до плоскости , если известно, что SC =5, AC =6 .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Дальний Восток. Вариант Р.Я.
а) сечение пирамиды плоскостью является прямоугольником.
1-й способ (метод координат).
Пусть точка O – центр равностороннего треугольника, BH – высота ,
Введем прямоугольную систему координат, как показано на рисунке: точка A – начало отсчета; оси x , y , z лучи AC , AV , AW соответственно, где лучи AV и BH сонаправлены, луч AW сонаправлен с лучом OS . Пусть AB = m , AS = k . Тогда координаты точек: .
Координаты некоторых точек найдем более подробно: , так как в равностороннем треугольнике высота является медианой и биссектрисой треугольника; ,так как катет равен произведению гипотенузы на синус противолежащего угла; , так как медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины; по теореме Пифагора .
Координаты этих точек находим из векторных равенств и
Уравнение плоскости и меет вид . Так как из параллельности прямой и плоскости получим .
Подставляя координаты точек P и K в уравнение плоскости и определения скалярного произведения векторов получим систему уравнений.
Значит уравнение плоскости где — вектор нормали к плоскости .
Найдем точку M – точку пересечения прямой AS и плоскости , уравнение прямой AS : пусть , тогда и получим уравнение прямой AS в параметрическом виде и подставляя его в уравнение плоскости получим Получим .
Найдем точку N – точку пересечения прямой CS и плоскости , уравнение прямой CS : пусть , тогда и получим уравнение прямой CS в параметрическом виде и подставляя его в уравнение плоскости получим Получим .
Получили четырехугольник MNKP – сечение пирамиды плоскостью . Докажем, что MNKP – параллелограмм, так как , то , значит MNKP – параллелограмм. Докажем, что MNKP – прямоугольник, так как , значит , тогда и MNKP – прямоугольник, что и требовалось доказать.
б) Расстояние от точки S до плоскости найдем по
По условию , значит . Тогда – расстояние от точки S до плоскости .
Решение: 2-й способ (геометрический метод).
а) сечение пирамиды плоскостью является прямоугольником.
Так как AP : PB = CK : KB =2:3 , то BP : BA = BK : BC =3:5 , значит по пропорциональности двух сторон и равенству углов между ними, тогда и эти углы являются соответственными углами для прямых PK и AC , и секущей AS , поэтому .
На грани SCB проведем прямую , на грани SAB проведем прямую , проведем отрезок MN в грани SAC , отрезок PK в грани ABC и получим PKNM – четырехугольник, который является сечением пирамиды плоскостью .
по двум углам: общий, как соответственные углы при параллельных прямых KN и BS , и секущей CB . Тогда получим, что соответствующие стороны пропорциональны, то есть CK : CB = CN : CS = KN : BS =2:5, значит .
по двум углам: общий, как соответственные углы при параллельных прямых PM и BS , и секущей AB . Тогда получим, что соответствующие стороны пропорциональны, то есть AP : AB = AM : AS = PM : BS =2:5 , значит .
Следовательно, , значит PKNM – параллелограмм, так как противоположные стороны параллельны и равны.
Прямые и прямая BH является проекцией прямой BS , тогда по теореме о трех перпендикулярах . Поэтому будут перпендикулярны соответственно параллельные им прямые PM и PK , поэтому и PKNM – прямоугольник, что и требовалось доказать.
б) Проведем высоту BH в треугольнике АВС , которая пересекает отрезок PK в точке R . SH является высотой боковой грани ACS и пересекает MN в точке T . Получим . Так как по пропорциональности двух сторон и равенству углов между ними BK : BC = BP : BA =3:5 , а значит и их высоты BR : BH =3:5.
Так как по пропорциональности двух сторон и равенству углов между ними NS : CS = MS : AS =3:5 , а значит и их высоты ST : SH =3:5.
Тогда HT : HS = HR : HB =2:5 и – общий угол, значит поэтому и эти углы являются соответственными углами для прямых RT и BS , и секущей HS , поэтому и высоты этих треугольников относятся как 2:5.
Значит , где площадь найдем по формуле Герона: BS =5, , , , .
Задание № 14 на ЕГЭ — 2019 по математике, профиль. Дидактические материалы.
Основная волна 29.05.2019.
№ 1.1.(а) В правильной треугольной пирамиде SABC точка P — делит сторону AB в отношении 2:3, считая от вершины A , точка K — делит сторону BC в отношении 2:3, считая от вершины C . Через точки P и K параллельно SB проведена плоскость .
а) Докажите, что сечение пирамиды плоскостью является прямоугольником.
б) Найдите расстояние от точки S до плоскости , если известно, что SC =5, AC =6 .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Дальний Восток. Вариант Р.Я.
№ 1.2.(а) В правильной треугольной пирамиде SABC сторона основания AB = 9, а боковое ребро SA = 6 . На рёбрах AB и SC отмечены точки K и M соответственно, причём AK:KB = SM:MC = 2:7 . Плоскость содержит прямую KM и параллельна прямой SA .
а) Докажите, что плоскость делит ребро SB в отношении 2:7, считая от вершины S .
б) Найдите расстояние между прямыми SA и KM .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. С.Петербург. Вариант Р.Я.
№ 1.3.(а) В правильной треугольной пирамиде SABC сторона основания AB = 4, а боковое ребро SA = 3 . На рёбрах AB и SC отмечены точки K и M соответственно, причём AK:KB = SM:MC = 3:1 . Плоскость содержит прямую KM и параллельна прямой SA .
а) Докажите, что сечение пирамиды SABC плоскость является прямоугольником.
б) Найдите объем пирамиды, вершиной которой является точка А, основание – сечение пирамиды плоскостью .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант Я.
№ 1.3.(б) В правильной треугольной пирамиде SABC сторона основания AB = 6, а боковое ребро SA = 5 . На рёбрах AB и SC отмечены точки K и M соответственно, причём AK:KB = SM:MC = 5:1 . Плоскость содержит прямую KM и параллельна прямой SA .
а) Докажите, что сечение пирамиды SABC плоскостью является прямоугольником.
б) Найдите объем пирамиды, вершиной которой является точка А, основание – сечение пирамиды плоскостью .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант .Л.
№ 1.4.(а) В правильной треугольной пирамиде SABC точка K — делит сторону SC в отношении 1:2, считая от вершины S , точка N — делит сторону SB в отношении 1:2, считая от вершины S . Через точки N и K параллельно SA проведена плоскость .
а) Докажите, что сечение пирамиды плоскостью параллельно прямой BC .
б) Найдите расстояние от точки B до плоскости , если известно, что SA =9, AB =6 .
Отве: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Центр Вариант Р.Я.
№ 1.5.(а) В правильной треугольной пирамиде SABC сторона основания AB равна 5, а боковое ребро SA равно 3. На ребрах AB и SC отмечены точки K и М соответственно, причем АК : КВ = SM : MC = 1:4. Плоскость содержит прямую КМ и параллельна прямой SA .
а) Докажите, что плоскость делит ребро AC в отношении 1:4, считая от вершины А .
б) Найдите расстояние между прямыми SA и KM .
Ответ: . Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант М.
№ 1.6.(а) В правильной треугольной пирамиде SABC сторона основания AB =3 , а боковое ребро SA =2 . На рёбрах AB и SC отмечены точки K и M соответственно, причём AK : KB = SM : MC =1:2. Плоскость содержит прямую KM и параллельна SA .
а) Докажите, что плоскость делит ребро AC в отношении 1:2, считая от вершины A .
б) Найдите расстояние между прямыми SA и KM .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №316.Р.
№ 1.7.(а) В правильной треугольной пирамиде SABC сторона основания AB =3 , а боковое ребро SA =4 . На рёбрах AB и SC отмечены точки K и M соответственно, причём AK : KB = SM : MC =1:2 . Плоскость содержит прямую KM и параллельна BC .
а) Докажите, что плоскость параллельна прямой SA .
б) Найдите угол между плоскостями и SBC .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №324.Я.
№ 1.7.(б) В правильной треугольной пирамиде SABC сторона основания AB =6 , а боковое ребро SA =7 . На рёбрах AB и SC отмечены точки K и M соответственно, причём AK : KB = SM : MC =1:5 . Плоскость содержит прямую KM и параллельна BC .
а) Докажите, что плоскость параллельна прямой SA .
б) Найдите угол между плоскостями и SBC .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №324.Я.
№ 1.8.(а) В правильной четырехугольной пирамиде SABCD AB=7; AS=14. На сторонах CD и SC взяты точки N и K соответственно, причем DN:NC=SK:KC=2:5 . Плоскость содержит прямую NK и параллельна ребру AS .
а) Докажите, что плоскость параллельна ВС .
б) Найдите расстояние от точки B до плоскости .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант Л.А.Я.
№ 1.9.(а) В правильной четырёхугольной пирамиде SABCD сторона основания AB= 4 , а боковое ребро SA = 8 . На рёбрах CD и SC отмечены точки N и K соответственно, причём DN:NC = SK:KC =1:3 . Плоскость α содержит прямую KN и параллельна прямой BC .
а) Докажите, что плоскость делит ребро AB в отношении 1:3, считая от вершины A .
б) Найдите расстояние между прямыми SA и KN .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №405.Р.
№ 1.9.(б) В правильной четырёхугольной пирамиде SABCD сторона основания AB=8 , а боковое ребро SA=10 . На рёбрах CD и SC отмечены точки N и K соответственно, причём DN:NC = SK:KC =1:7. Плоскость содержит прямую KN и параллельна прямой BC .
а) Докажите, что плоскость делит ребро SB в отношении 1:7, считая от вершины S .
б) Найдите расстояние между прямыми SA и KN .
Ответ:б) Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №409.Р.Я.
№ 1.10.(а) В правильном тетраэдре ABCD точки K и M — середины рёбер AB и CD соответственно. Плоскость содержит прямую KM и параллельна прямой AD .
а) Докажите, что сечение тетраэдра плоскостью — квадрат.
б) Найдите площадь сечения тетраэдра ABCD плоскостью, если
Ответ:б)3 Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант №991.Р.
№ 1.11.(а) В правильной треугольной пирамиде SABC сторона основания AB =6 , а боковое ребро SA =7 . На рёбрах AB и SC отмечены точки K и M соответственно, причём AK : KB = SM : MC =5:1 . Плоскость содержит прямую KM и параллельна прямой BC .
а) Докажите, что сечение пирамиды SABC плоскостью является прямоугольником .
б) Найдите расстояние от точки C до плоскости угол .
Ответ: Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант № .Я.
№ 1.12.(а) В правильной четырёхугольной пирамиде SABCD сторона основания AB=3 , а боковое ребро SA=6 . Точка K делит ребро SC , причём SK:KC =1:2. Плоскость проходит через точку K и параллельна плоскости SAD .
а) Докажите, что сечение пирамиды плоскостью является равнобедренной трапецией.
б) Найдите объем пирамиды, вершиной которой является точка S , а основание – сечение пирамиды SABC D плоскостью .
Ответ:б) Источник: ЕГЭ — 2019. Основная волна 29.05.2019. Вариант № .Я.
Основная волна. Резерв. 24.06.2019.
№ 1.13.(а) В правильной треугольной призме сторона основания равна 4, а боковое ребро равно 2. Точка M — середина ребра , а точка O — точка пересечения диагоналей боковой грани .
а) Докажите, что точка пересечения диагоналей четырёхугольника, являющегося сечением призмы плоскостью AMB лежит на отрезке .
б) Найдите угол между прямой , и плоскостью AMB .
Ответ: Источник: ЕГЭ — 2019. Основная волна. Резерв. 24.06.2019. Вариант №503.и Кавказ. Р.
№ 1.13.(б) В правильной треугольной призме сторона основания равна 4, а боковое ребро равно 6. Точка M — середина ребра , а точка O — точка пересечения диагоналей боковой грани .
а) Докажите, что точка пересечения диагоналей четырёхугольника, являющегося сечением призмы плоскостью AMB лежит на отрезке .
б) Найдите угол между прямой , и плоскостью AMB .
Ответ: Источник: ЕГЭ — 2019. Основная волна. Резерв. 24.06.2019. Вариант Л.
№ 1.14.(а) В кубе рёбра равны 1. На продолжении отрезка за точку отмечена точка M так, что , а на продолжении отрезка за точку C отмечена точка N так, что .
б) Найдите расстояние между прямыми и MN .
Ответ: Источник: ЕГЭ — 2019. Основная волна. Резерв. 24.06.2019. Вариант 992.Р.
Досрочная волна (29.03.19).
а) Докажите, что ребро SA перпендикулярно ребру BC .
б) Найдите расстояние между ребрами BC и SA .
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. 29.03.2019. Вариант
а) Докажите, что ребро SA перпендикулярно ребру BC .
б) Найдите расстояние между ребрами BC и SA .
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. 29.03.2019. Вариант
№ 1.16.(а) В треугольной пирамиде PABC с основанием ABC известно, что AB =13, PB =15, . Основанием высоты этой пирамиды является точка C . Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC .
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. 29.03.2019. Вариант
Досрочная волна, резерв. (10.04.19).
№ 1.17.(а) В конусе с вершиной S и центром основания O , радиус основания равен 13, а высота равна . Точки A и B – концы образующих, M – середина SA , N – точка в плоскости основания такая, что прямая MN параллельна прямой SB .
б) Найдите угол между прямой MB и плоскостью основания конуса, если известно, что AB =10 .
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. Резерв. 10.04.2019. Вариант
№ 1.17.(б) В конусе с вершиной S и центром основания O , радиус основания равен 5, а высота равна . Точки A и B – концы образующих, M – середина SA , N – точка в плоскости основания такая, что прямая MN параллельна прямой SB .
б) Найдите угол между прямой MB и плоскостью основания конуса , если известно, что AB =8 .
Ответ: Источник: ЕГЭ — 2019. Досрочная волна.. Резерв. 10.04.2019. Вариант
🔥 Видео
СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Сечение Пирамиды Плоскостью Параллельной боковому ребруСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ЕГЭ Задание 14 Правильная пирамида Площадь сеченияСкачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

Как строить сеченияСкачать

Стереометрия 19 | mathus.ru | угол между плоскостью и прямой в правильной треугольной пирамидеСкачать

Параллельность прямой к плоскостиСкачать

Построение линии пересечения поверхности пирамиды с проецирующей плоскостьюСкачать

Точка встречи прямой с плоскостьюСкачать

Построение сечения пирамиды. Метод следов.Скачать

№3. Как строить сечения пирамидСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать