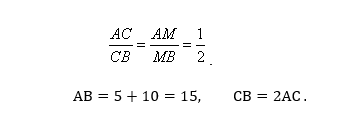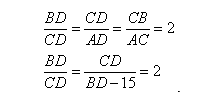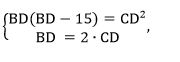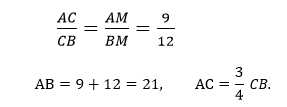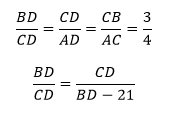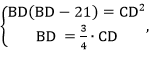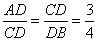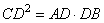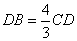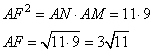В треугольнике известны стороны окружность проходящая через точки пересекает (3 видео)

В треугольнике известны стороны окружность проходящая через точки пересекает

Задания С4 ЕГЭ 2012 — образцы вариантов всех «волн» с критериями

Досрочный ЕГЭ (Апрель)

Боковые стороны KL и MN трапеции KLMN равны 8 и 17 соответственно. Отрезок, соединяющий середины диагоналей, равен 7,5, средняя линия трапеции равна 17,5. Прямые KL и MN пересекаются в точке А. Найдите радиус окружности, вписанной в треугольник ALM.

Основная волна (Июнь)

В треугольнике АВС известны стороны АВ=7, ВС=8, АС=9. Окружность, проходящая через точки А и С, пересекает прямые ВА и ВС соответственно в точках К и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник АВС. Найдите длину отрезка KL.

Основная волна (Июнь — Восток)

Дан равнобедренный треугольник с боковой стороной 4 и углом 120 0 . Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.

Основная волна (резервный день)

Точка О — центр правильного шестиугольника ABCDEF со стороной 14sqrt(3). Найдите радиус окружности, касающейся окружностей, описанных около треугольников АОВ, COD и EOF.

Вторая волна (Июль)

Продолжение би c сектрисы CD неравнобедренного треугольника АВС пересекает окружность, описанную около этого треугольника, в точке Е. Окружность, описанная около треугольника ADE, пересекает прямую АС в точке F, отличной от А. Найдите радиус окружности, описанной около треугольника АВС, если АС=8, AF=3, угол ВАС равен 45 0 .

Вторая волна (Резервный день)

Угол С треугольника АВС равен 60 0 , D — отличная от А точа пересечения окружностей, построенных на сторонах АВ и АС как на диаметрах. Известно, что DB:DC=2:3. Найдите угол А.

Дополнительный вариант (999)

На прямой, содержащей медиану AD прямоугольного треугольника АВС с прямым углом С, взята точка Е, удаленная от вершины А на расстояние, равное 4. Найдите площадь треугольника ВСЕ, если ВС=6, АС=4?

Содержание

Задание №188
Условие
Решение
Задание №25 ОГЭ по математике
📹 Видео

Видео:✓ Самая сложная задача в ОГЭ-2020 | Задание 26. Математика | Геометрия | Борис ТрушинСкачать

Задание №188

Видео:ОГЭ Задание 26 Подобные треугольникиСкачать

Условие

В треугольнике ABC окружность проходит через точки B и C и пересекает стороны AB и AC в точках M и N соответственно. Отрезок MN касается окружности, вписанной в треугольник ABC .

а) Докажите, что bigtriangleup ABC подобен bigtriangleup ANM .

б) Найдите MN , если AB=7, AC=8, BC=9 .

Видео:Математика ОГЭ. Задача 26_4Скачать

Решение

а) Окружность с центром в точке O_1 описана около четырехугольника BMNC , значит, angle BCN+angle BMN =180^ , angle BMN=180^-angle BCN . angle AMN+angle BMN=180^ , как смежные, angle BMN=180^-angle AMN.

Отсюда angle BCN=angle AMN .

Имеем в треугольниках ABC и ANM : angle A — общий, angle ACB=angle NCB=angle AMN, значит, bigtriangleup ABC подобен bigtriangleup ANM по первому признаку подобия, что требовалось доказать.

Окружность с центром в точке O вписана в bigtriangleup ABC, значит

AF=AE, BE=BP, CP=CF , как отрезки касательных, проведенных к окружности c центром O_1 из точек A, B и C соответственно.

Пусть AF=AE=x, тогда BE=BP=7-x, CP=CF=8-x, BP+CP=BC, 7-x+8-x=9, x=3, AF=AE=3 .

Обозначим MK=t, NK=p, тогда ME=MK=t, NF=NK=p как отрезки касательных, проведенных к окружности с центром O из точек M и N соответственно.

Получим AM=AE-ME=3-t, AN=AF-NF=3-p, MN=MK+NK=t+p .

Периметр bigtriangleup AMN равен AM+AN+MN=3-t+3-p+t+p=6.

Периметры подобных треугольников относятся так же как и их стороны, поэтому frac=frac, MN=frac=2,25

Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Задание №25 ОГЭ по математике

Решаем сложную геометрическую задачу.

Алгоритм решения:

Делаем чертеж.
Определяем равенство угла между касательной и хордой и угла АВС.
Определяем соотношение отрезков из свойства биссектрисы угла треугольника и найдем АВ.
Показываем, что треугольники DAC и DCB подобны.
Составляем соотношения сторон подобных треугольников.
Составляем систему равенств.
Решаем систему.
Записываем ответ.

Решение:

2. Рассматриваем АСD. В нем:

Согласно свойству углов окружности, касательной и секущей, угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла. ∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА. Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD. 3. Согласно свойству биссектрисы угла треугольника, она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,

4. Рассмотрим DAC и DCB. У них:

∠ DCA = ∠ DBC по доказанному выше,

Следовательно, DAC DCB по двум углам.

5. Из определения и свойств подобных треугольников имеем:

6. Составим систему равенств:

7. Решим систему:

Ответ: 10

pазбирался: Даниил Романович | обсудить разбор | оценить

Алгоритм решения:

Сделаем чертеж.
Определим равенство углов CDB и АВС.
Определим соотношение отрезков, воспользовавшись свойством биссектрисы угла треугольника, и определим длину АВ.
Покажем, что треугольники DAC и DCB подобны.
Составим соотношения сторон подобных треугольников.
Составим систему равенств.
Решим систему.
Запишем ответ.

Решение:

2. Рассмотрим АСD. В нем, согласно свойству углов окружности, касательной и секущей, угол, который образован этими линиями, равен половине градусной меры дуги, заключенной между сторонами этого угла. ⇒∠DСА равен половине градусной меры дуги АС, заключенной между его сторонами СD и СА. Но вписанный ∠СВА опирается на ту же дугу АС и по свойству вписанного угла равен половине меры этой дуги. Следовательно, ∠ СВА=∠ АСD. 3. Согласно свойству биссектрисы угла треугольника, согласно которому она делит АВ на отрезки АМ и МВ, пропорциональные сторонам АС и ВС. Таким образом,

4. Рассмотрим DAC и DCB. У них:

∠ DCA = ∠ DBC по доказанному выше,

Значит, DAC DCB по двум углам.

5. Из определения и свойств подобных треугольников имеем:

6. Составим систему равенств:

7. Решим систему:

Так как AD = DB-21, имеем:

Таким образом, искомая длина CD=36.

pазбирался: Даниил Романович | обсудить разбор | оценить

Алгоритм решения:

Сделаем чертеж.
Установим подобие треугольников AFM и ANF.
Определим сторону FM.
Определим ∠FNA.
Найдем .
Составим теорему синусов и найдем радиус окружности.
Запишем ответ.

Решение:

1. Рассмотрим треугольники AFM и ANF. У них:

Угол A является общим, а

по доказанному выше.

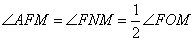
Следовательно, треугольник AFM подобен треугольнику ANF по двум углам. Отсюда вытекает:

3. В треугольнике AFM сторона AF=3, сторона AM=9. Воспользуемся теоремой косинусов для определения FM:

Полученное значение означает, что AFM является равнобедренным. У него основание AF. 4. По свойству равнобедренного треугольника ∠FAM=∠AFM. Отсюда 5. Найдем Значит, 6. Из FMN по теореме синусов: где R – радиус описанной окружности. Отсюда получим значение радиуса окружности: Ответ: 5,4

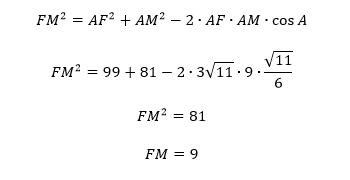
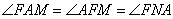
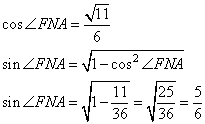
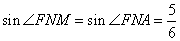
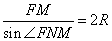
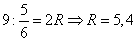
pазбирался: Даниил Романович | обсудить разбор | оценить

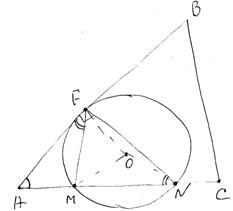
Пусть O — центр данной окружности, а Q — центр окружности, вписанной в треугольник ABC .

Точка касания M окружностей делит AC пополам по условию.

Лучи AQ и AO — биссектрисы смежных углов, так как касательные к окружностям равноудалены от центра. Так как AQ и AO — биссектрисы смежных углов, то угол OAQ прямой — смежные углы в сумме дают 180°, значит сумма их биссектрис:

Далее рассмотрим прямоугольный треугольник OAQ. По свойству высоты в прямоугольном треугольнике, получаем:

AM² = MQ•MO Отсюда:

pазбирался: Даниил Романович | обсудить разбор | оценить

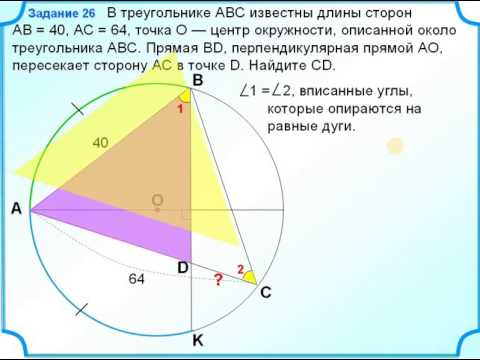
Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить