Теорема о периметре треугольника (5 видео)

Нахождение периметра треугольника: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.

Содержание

Формула вычисления периметра
Примеры задач
Как найти периметр треугольника
Определение
Как узнать периметр треугольника
Скачать онлайн таблицу
Как найти периметр треугольника если известны не все стороны
Первый метод: известны все стороны фигуры
Второй метод: прямоугольный треугольник и две известные его стороны
Третий метод: по двум граням и углу между ними
🎥 Видео

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Формула вычисления периметра

Периметр (P) любого треугольника равняется сумме длин всех его сторон.

P = a + b + c

Периметр равнобедренного треугольника

Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:

P = a + 2b

Периметр равностороннего треугольника

Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:

P = 3a

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Примеры задач

Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.

Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.

Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.

Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Как вычислить периметр #геометрия #задача #треугольник #периметрСкачать

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Видео:Треугольники. 7 класс.Скачать

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Как найти периметр треугольника если известны не все стороны

Периметр — это величина, подразумевающая длину всех сторон плоской (двумерной) геометрической фигуры. Для разных геометрических фигур существуют разные способы нахождения периметра.

В данной статье вы узнаете как находить периметр фигуры разными способами, в зависимости от известных его граней.

Возможные методы:

известны все три стороны равнобедренного или любого другого треугольника;
как найти периметр прямоугольного треугольника при двух известных его гранях;
известны две грани и угол, который расположен между ними (формула косинусов) без средней линии и высоты.

Это интересно: что микроэкономика изучает, кратко об основателях и основах науки.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Первый метод: известны все стороны фигуры

Как находить периметра треугольника, когда известны все три грани, необходимо использовать следующую формулу: P = a + b + c, где a,b,c — известные длины всех сторон треугольника, P — периметр фигуры.

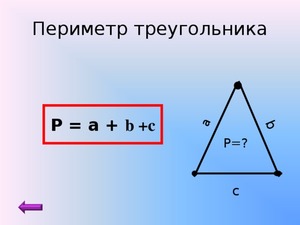
Например, известны три стороны фигуры: a = 24 см, b = 24 см, c = 24 см. Это правильная равнобедренная фигура, чтобы вычислить периметр пользуемся формулой: P = 24 + 24 + 24 = 72 см.

Данная формула подходит к любому треугольнику, необходимо просто знать длины всех его сторон. Если хотя бы одна из них неизвестна, необходимо воспользоваться другими способами, о которых мы поговорим ниже.

Еще один пример: a = 15 см, б = 13 см, c = 17 см. Вычисляем периметр: P = 15 + 13 + 17 = 45 см.

Очень важно помечать единицу измерения в полученном ответе. В наших примерах длины сторон указаны в сантиметрах (см), однако, существуют разные задачи, в условиях которых присутствуют другие единицы измерения.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Второй метод: прямоугольный треугольник и две известные его стороны

В том случае, когда в задании, которое нужно решить, дана прямоугольная фигура, длины двух граней которой известны, а третья нет, необходимо воспользоваться теоремой Пифагора.

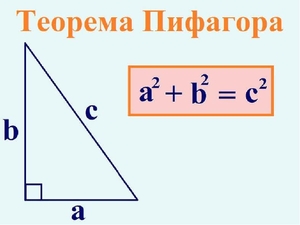
Теорема Пифагора описывает соотношение между гранями прямоугольного треугольника. Формула, описываемая этой теоремой, является одной из самых известных и наиболее часто применяемых теорем в геометрии. Итак, сама теорема:

Стороны любого прямоугольного треугольника описываются таким уравнением: a^2 + b^2 = c^2, где а и b — катеты фигуры, а c — гипотенуза.

Гипотенуза. Она всегда расположена противоположно прямому углу (90 градусов), а также является самой длинной гранью треугольника. В математике принято обозначать гипотенузу буквой c.
Катеты — это грани прямоугольного треугольника, которые относятся к прямому углу и обозначаются буквами а и b. Один из катетов одновременно является и высотой фигуры.

Таким образом, если условиями задачи заданы длины двух из трех граней такой геометрической фигуры, с помощью теоремы Пифагора необходима найти размерность третьей грани, после чего воспользоваться формулой из первого метода.

Например, мы знаем длину 2-х катетов: a = 3 см, b = 5 см. Подставляем значения в теорему: 3^2 + 4^2 = c^2 => 9 + 16 = c^2 => 25 = c^2 => c = 5 см. Итак, гипотенуза такого треугольника равна 5 см. К слову, данный пример является самым распространенным и называется «Египетский треугольник». Иными словами, если два катета фигуры равны 3 см и 4 см, то гипотенуза составит 5 см соответственно.

Если неизвестна длина одного из катетов, необходимо преобразовать формулу следующим образом: c^2 — a^2 = b^2. И наоборот для другого катета.

Продолжим пример. Теперь необходимо обратиться к стандартной формуле поиска периметра фигуры: P = a + b + c. В нашем случае: P = 3 + 4 + 5 = 12 см.

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Третий метод: по двум граням и углу между ними

В старшей школе, а также университете, чаще всего приходится обращаться именно к данному способу нахождения периметра. Если условиями задачи заданы длины двух сторон, а также размерность угла между ними, то необходимо воспользоваться теоремой косинусов.

Данная теорема применима абсолютно к любому треугольнику, что и делает ее одной из наиболее полезных в геометрии. Сама теорема выглядит следующим образом: c^2 = a^2 + b^2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.

Представим, что описан треугольник, стороны а и б которого составляют 100 см и 120 см соответственно, а угол, лежащий между ними, составляет 97 градусов. То есть а = 100 см, б = 120 см, C = 97 градусов.

Все, что нужно сделать в данном случае — это подставить все известные значения в теорему косинусов. Длины известных граней возводятся в квадрат, после чего известные стороны перемножаются между друг другом и на два и умножаются на косинус угла между ними. Далее, необходимо сложить квадраты граней и отнять от них второе полученное значение. Из итоговой величины извлекается квадратный корень — это будет третья, неизвестная до этого сторона.

После того как все три грани фигуры известны, осталось воспользоваться уже полюбившейся нам стандартной формулой поиска периметра описываемой фигуры из первого метода.