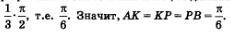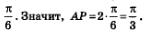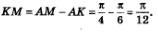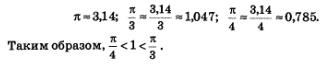Вторая четверть числовой окружности разделена пополам точкой

Видео:Как искать точки на тригонометрической окружности.Скачать

Введение

Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика: Введение, окружность, вычитание, числовая окружность, математический язык

В курсе алгебры 7—9-го классов вы изучали алгебраические функции, т.е. функции, заданные аналитическими выражениями, в записи которых использовались алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение квадратного корня). Но математические модели реальных ситуаций часто бывают связаны с функциями других классов, не алгебраическими. В школьном курсе математики это показательные, логарифмические и тригонометрические функции. Мы приступаем сейчас к изучению тригонометрических функций.

Для введения тригонометрических функций нам понадобится новая математическая мгодель — числовая окружность, детальному изучению которой посвящен § 2, достаточно большой параграф. От- 4, неситесь к нему очень внимательно, поскольку, как показывает » опыт, учащийся, хорошо овладевший понятием «числовая окружность», свободно и непринужденно работающий с ней, достаточно уверенно обращается и с тригонометрическими функциями. Для облегчения восприятия материала о числовой окружности рассмотрим ряд вспомогательных геометрических примеров.

Пример 1. Дана окружность радиусом 1см. Чему равна длина окружности, ее половины, ее четверти?
Решение. Длина L окружности радиусом R вычисляется по формуле

В дальнейшем будем говорить об окружности, радиус которой равен масштабному отрезку, без указания конкретных единиц измерения. Радиус такой окружности считается равным 1, а саму окружность называют единичной. Мы все время будем пользоваться единичной окружностью, в которой проведены горизонтальный и вертикальный диаметры СА и 2)Б. Условимся называть дугу АВ (см. рис. 1) первой четвертью, дугу ВС — второй четвертью, дугу С2) — третьей четвертью, дугу ДА — четвертой четвертью. При этом, как правило, речь идет об открытых дугах, т.е. о дугах без их концов: например, первая четверть — это ду га АВ без точек А и В.

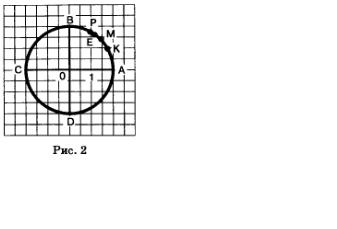
Пример 2. В единичной окружности проведены два взаимно перпендикулярных диаметра: горизонтальный СА и вертикальный БВ. Дуга АВ разделена точкой М на две равные части, а точками К и Р — на три равные части (рис. 2). Чему равны длины дуг АМ. МВ, АК, КР, РВ.АР и КМ?

Решение. Так как длина дуги АВ равна

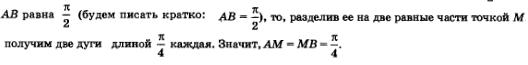
Если дуга АВ разбита на три равные части точками К и Р,то длина каждой полученной части равна

Дуга АР состоит из двух дуг АК и КР длиной
Осталось вычислить длину дуги КМ. Эта дуга получается из дуги АМ отбрасыванием дуги АК. Значит, длина дуги КМ равна разности длин дуг АМ и АК. Таким образом,

Замечание. Обратите внимание на некоторую вольность, которую мы позволяем себе в использовании алгебраического языка. Ясно, что дуга КМ и длина дуги КМ — разные вещи (первое понятие — геометрическая фигура, а второе понятие — число). А обозначается и то, и другое одинаково: КМ. Более того, если точки К и М соединить отрезком, то и полученный отрезок, и его длина обозначаются так же: КМ. Обычно из контекста бывает ясно, какой смысл вкладывается в обозначение (дуга, длина дуги, отрезок или длина отрезка).

А теперь еще раз взгляните на рис. 1. Сколько вы видите дуг единичной окружности, соединяющих точки А и Б? Две: поменьше, если идти от точки А к точке Б по первой четверти, и побольше, если идти от точки В к точке А по второй, третьей и четвертой четвертям. Как же отличать эти дуги друг от друга в символах математического языка? Условимся в двухбуквенном обозначении дуги на первом месте писать букву, соответствующую началу дуги, а на втором — букву, соответствующую концу дуги, причем движение по окружности от начала дуги к ее концу будем осуществлять в направлении против часовой стрелки. Тогда меньшая из двух дуг, соединяющих точки А и Б, о которых мы говорили выше, — это дуга АВ, а большая — это дуга БА.

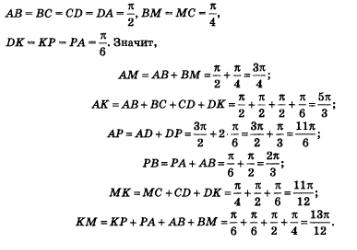
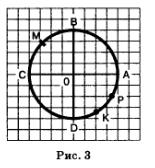
Пример 3. Вторая четверть единичной окружности разделена пополам точкой М (рис. 3), а четвертая четверть разделена на три равные части точками КиР. Чему равны длины дуг АМ, АК, АР, РВ, МК, КМ?

Решение. Прежде чем переходить к требуемым вычислениям, заметим, что

Заметили ли вы, что во всех разобранных примерах длины дуг выражались некоторыми долями числа я? Это неудивительно: ведь длина единичной окружности равна 2я, и если мы окружность или ее четверть делим на равные части, то получаются дуги, длины которых выражаются долями числа я. А как вы думаете, можно ли найти на единичной окружности такую точку Е, что длина дуги АЕ будет равна 1? Давайте прикинем:

Обратимся снова к рис. 2. Если АЕ = 1, то точка Е находится между точками М и Р, ближе к точке Р. Разумеется, точно (а не приблизительно) указать положение точки Е на окружности мы не сумеем, но это, впрочем, не так уж важно.

Рассуждая аналогичным образом, делаем вывод, что на единичной окружности можно найти и точку Е₁, для которой АЕ₁ = 1, и точку Е₂, для которой АЕ₂= 2, и точку Е₃, для которой АЕ₃ = 3, и точку Е₄, для которой АЕ₄ = 4, и точку Е₅, для которой АЕ₅ = 5, и точку Е₆, для которой АЕ₆ = 6. На рис. 4 отмечены (приблизительно) соответствующие точки, причем для ориентировки каждая из четвертей единичной окружности разделена черточками на три равные части.

А.Г. Мордкович Алгебра 10 класс

_{Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике видео скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Сборник задач по теме «Тригонометрия»
методическая разработка на тему

Представлен сборник заданий на применении основных формул тригонометрии

Видео:Тригонометрическая окружность. Как выучить?Скачать

Скачать:

Видео:Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

Предварительный просмотр:

по дисциплине «Математика»

на тему: «Сборник задач по теме «Тригонометрия»

Выполнила: Разиева Т.С.

Программа учебной дисциплины «Математика» предназначена для реализации государственных требований к минимуму содержания и уровню подготовки выпускников по специальностям среднего профессионального образования и является единой для всех форм обучения.

Сборник задач по теме «Тригонометрия» разработан в соответствии с федеральными государственными образовательными стандартами. Предложенные задачи по тригонометрии применяются на занятиях по математике для обучающихся 1 курса всех специальностей.

Данные задачи могут быть использованы на семинарах, практических занятиях и лекциях. Предлагаемые задачи помогут преподавателю создать необходимое мотивационное пространство, позволят использовать на занятии элементы проблемного и дифференцированного обучения. Все задания разделены между собой:

• Задачи вида 1, 5, 41 и т.д. предназначены для самостоятельного решения или для работы на занятии.
• Задачи вида 6, 30, 117 и т.д. предназначены для домашней работы.
• Задачи вида 14, 22 носят дифференцированный и проблемный характер.

Создание мотивационного пространства возможно с помощью предложенных задач. В конце задачника дан необходимый для решения задач справочный материал с основными тригонометрическими формулами.

Использование данной разработки на занятиях имеет следующие преимущества:

• обучающиеся могут самостоятельно выбирать и выполнять задания;
• задания различного уровня сложности позволяют не только закрепить изученный материал, но и оперативно оценить уровень знаний каждого студента.

1. Считая числовую окружность образом беговой дорожки стадиона, отметьте на ней конец дистанции: а) 1500 м; б) 42 км 195 м.

2 . Дана окружность радиуса 1 см. Чему равна длина: а) всей окружности; б) ее половины; в) ее четверти?

Горизонтальный диаметр СА и вертикальный диаметр DB разбивают единичную окружность на четыре четверти: АВ – первая, ВС – вторая, CD – третья, DA – четвертая.

Опираясь на эту геометрическую модель, решите задачи № 3, 4, 5, 6, 7, 8.

3 . Первая четверть разделена точкой М на две равные части, а точками К и Р – на три равные части (точка Р между М и В ). Чему равна длина дуги: АМ , МВ , АК , КР , РВ , АР , КМ ?

4 . Вторая четверть разделена пополам точкой М , а третья четверть разделена на три равные части точками К и Р (точка Р между К и D ). Чему равна длина дуги: АМ , ВК , МР , DC , КА , ВР , СВ , ВС ?

5 . Вторая четверть разделена точкой М пополам, а четвертая четверть разделена на три равные части точками К и Р (точка Р между К и А ). Чему равна длина дуги: АМ , АК , АР , РВ , МК , КМ ?

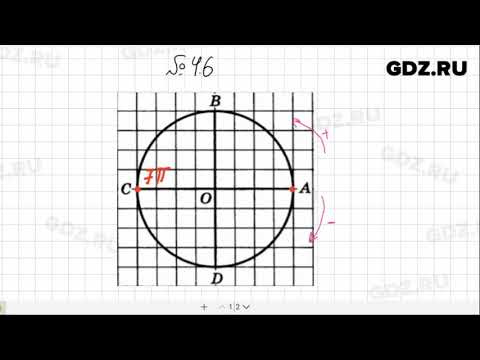
6 . Первая четверть разделена на две равные части точкой М , а четвертая разделена на три равные части точками К и Р (точка Р между К и А ). Чему равна длина дуги: АМ , ВD , CK , MP , DM , MK , СP , PС ?

7 . Третья четверть разделена точкой Р в отношении 1 : 5. Чему равна длина дуги: СР , PD , АР ?

8 . Первая четверть разделена точкой М в отношении 2 : 3. Чему равна длина дуги: АМ , МВ , DM , МС ?

9 . Выразите в радианах:

1) 1 °; 4) 10°; 7) 15°; 10) 30°;

2) 45°; 5) 60°; 8) 70°; 11) 90°;

3) 225°; 6) 240°; 9) 320°; 12) 330°.

10 . Переведите из градусной меры в радианную:

1) 120°; 3) 220°; 5) 300°; 7) 765°;

2) 210°; 4) 150°; 6) 315°; 8) 675°.

11 . Выразите в градусах:

1) π; 4) π; 7) π; 10) π;

2) π; 5) π; 8) 1,5π; 11) 3π;

3) 0,25π; 6) π; 9) – π; 12) π.

12 . Переведите из радианной меры в градусную:

1) π; 3) π; 5) π; 7) π;

2) π; 4) π; 6) π; 8) π.

13 . Окружность разделена на шесть равных частей. Выразить в градусах и радианах сумму дуг:

14 . Угол А трапеции ABCD ( AD || BC ) на 70° меньше угла В и на 10° больше угла D . Найдите радианную меру каждого из углов трапеции.

15 . Перечертите в тетрадь и заполните таблицу:

📽️ Видео

№ 4.2- Алгебра 10-11 класс МордковичСкачать

Точки на числовой окружностиСкачать

№ 4.6- Алгебра 10-11 класс МордковичСкачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Соответствие чисел точкам числовой окружностиСкачать

Числовая окружностьСкачать

Числовая окружность | Алгебра 10 класс #8 | ИнфоурокСкачать

ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

1. Числовая окружность. 10 классСкачать

Вычисление значений тригонометрических функцийСкачать

Числовая окружность (примеры)Скачать

10 класс - Алгебра - Числовая окружностьСкачать

Числовая окружность. Часть 2 практика - MirUrokov.ru - Видеоурок по математикеСкачать

Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать