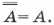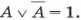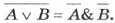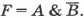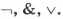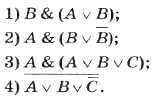Содержание:
Алгебра логики является частью, разделом бурно развивающейся сегодня науки — дискретной математики. Дискретная математика занимается изучением свойств структур конечного характера, которые возникают как внутри математики, так и в ее приложениях.
- Заметим, что классическая математика, в основном, занимается изучением свойств объектов непрерывного характера, хотя само деление математики на классическую и дискретную в значительной мере условно, поскольку между ними происходит активная циркуляция идей и методов, часто возникает необходимость исследовать модели, обладающие как дискретными, так и непрерывными свойствами.
К числу структур, изучаемых дискретной математикой, могут быть отнесены конечные группы, конечные графы, математические модели преобразователей информации типа конечных автоматов или машин Тьюринга и др. Математический аппарат алгебры логики широко используется в информатике, в частности, в таких ее разделах, как проектирование ЭВМ, теория автоматов, теория алгоритмов, теория информации, целочисленное программирование и т. д. Алгебра логики.
Понятие высказывания Алгебра логики изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству (например,
Именно он построил один из разделов формальной логики в виде некоторой «алгебры», аналогичной алгебре чисел, но не сводящейся к ней. Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами.
Существуют алгебры натуральных чисел, многочленов, векторов, матриц, множеств и т. д. Дж. Буль (1815-1864) Долгое время алгебра логики была известна достаточно узкому классу специалистов.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Прошло почти 100 лет со времени создания алгебры логики Дж. Булем, прежде чем в 1938 году выдающийся американский математик и инженер Клод Шеннон (1916-2001) показал, что алгебра логики применима для описания самых разнообразных процессов, в том числе функционирования ре-лейно-контактных и электронно-ламповых схем. Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики).
- С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно. Примерами высказываний на естественном языке являются предложения «Сегодня светит солнце» или «Трава растет». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в нашем примере погоды и окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь».
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 

Определение 1. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Возможно вам будут полезны данные страницы:
Это словесное определение, не являющееся математически точным, только на первый взгляд кажется удовлетворительным. Оно отсылает проблему определения высказывания к проблеме определения истинности или ложности данного языкового образования. Если рассматривать в качестве высказываний любые утвердительные предложения, то это быстро приводит к парадоксам и противоречиям. Например, предложению «Это предложение является ложным» невозможно приписать никакого значения истинности без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит его смыслу. Если же принять, что предложение ложно, то отсюда следует, что предложение на самом деле истинно.
- Как видно, этому предложению осмысленно нельзя приписать какое-либо значение истинности, следовательно, оно не является высказыванием. Причина этого парадокса лежит в структуре построения указанного предложения: оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя и, следовательно, устранены возникающие отсюда парадоксы.
Определение 2. Высказывание называется простым (элементарным)I, если никакая его часть не является высказыванием.
Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывание, соединив их знаком равенства или неравенства. Сами числовые выражения высказываниями не являются. Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «

Мы можем договориться, что абсурдное по смыслу высказывание «Крокодилы летают» является истинным, и с этим значением высказывания будем работать. Вопрос о том, летают крокодилы или нет, может волновать зоологов, но никак не математиков: им этот потрясающий факт безразличен. Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания. В информатике для точного определения понятия высказывания строятся ограниченные системы форм высказываний (формальный язык), которые используются при описании алгоритмических языков, в информационных системах, для строгого формального описания алгоритмов и т. д.
- Логические операции. Таблицы истинности
- Примеры с решением
- Логические формулы. Законы алгебры логики
- Математическая логика, преобразования
- Теория к заданию 18 из ЕГЭ по информатике
- Алгебра логики
- Алгебра логики
- Логические выражения и их преобразование
- Алгебра логики знаки и их обозначения
- Обозначения в логических операциях
- Свойства логических операций
- 1.3.1. Высказывание
- 1.3.4. Свойства логических операций
- 1.3.6. Логические элементы
- Самое главное
- Вопросы и задания
- Электронное приложение к уроку
- 📺 Видео
Логические операции. Таблицы истинности
Употребляемые в обычной речи связки «и», «или», «не», «если . то . », «тогда и только тогда, когда . » и т. п. позволяют из уже заданных высказываний строить новые сложные высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как логических операций над высказываниями. Для обозначения истинности, как правило, используются символы «И» и «1», а для обозначения ложности — символы «Л» и «0».
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний. В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:
Введем перечисленные логические операции формальным образом. Высказывание, составленное из двух высказываний путем объединения их связкой «и», называется конъюнкцией или логическим умножением. Высказывая конъюнкцию, мы утверждаем, что выполняются оба события, о которых идет речь в составляющих высказываниях.
Например, сообщая: , мы выражаем в одном высказывании свое убеждение в том, что произошли оба этих события.
Определение 3. Конъюнкция — логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Логическая операция конъюнкция определяется следующей таблицей, которую называют таблицей истинности:
Рассмотрим два высказывания 



Высказывание 
Высказывание, состоящее из двух высказываний, объединенных связкой «или», называется дизъюнкцией или логическим сложением, нестрогой дизъюнкцией.
В высказываниях, содержащих связку «или», указывается на существование двух возможных событий, из которых хотя бы одно должно быть осуществлено. Например, сообщая: <Петя читает книгу или пьет чай), мы имеем в виду, что хотя бы что-либо одно Петя делает. При этом Петя может одновременно читать книгу и пить чай. И в этом случае дизъюнкция будет истинна.
Определение 4. Дизъюнкция — логическая операция, которая каждым двум элементарным высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Логическая операция дизъюнкция определяется следующей таблицей истинности:
Дизъюнкция истинна, когда хотя бы одно из двух образующих ее высказываний истинно. Рассмотрим два высказывания 


Союз «или» может применяться в речи и в другом, «исключающем» смысле. Тогда он соответствует другому высказыванию — разделительной, или строгой дизъюнкции. 3.2.3. Высказывание, образованное из двух высказываний, объединенных связкой «либо» (точнее: «либо только . либо только . »), называется разделительной (строгой) дизъюнкцией, исключающим ИЛИ, сложением по модулю 2.
В отличие от обычной дизъюнкции (связка «или»), в высказывании, являющемся разделительной дизъюнкцией, мы утверждаем, что произойдет только одно событие из двух. Например, сообщая: , мы утверждаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б.
Определение 5. Строгая, или разделительная дизъюнкция — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда ровно одно из двух высказываний является истинным.
Логическая операция разделительная дизъюнкция определяется следующей таблицей истинности:
Рассмотрим два высказывания 


Определение 6. Импликация — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда условие (посылка) — истинно, а следствие (заключение) — ложно.
Логическая операция импликация задается следующей таблицей истинности:
Мы видим, что импликация заведомо истинна, если условие 

Примеры с решением
Пример 1.
Следующие две импликации являются ложными, так как в них посылки истинны, а заключения ложны:
Может показаться странным, что высказывание «Если А, то В>> всегда истинно, если посылка (высказывание Л) ложна. Но для математика это вполне естественно. В самом деле, исходя из ложной посылки, можно путем верных рассуждений получить как истинное, так и ложное утверждение. Допустим, что 1 = 2, тогда и 2 = 1. Складывая эти равенства, получим 3 = 3, т. е. из ложной посылки путем тождественных преобразований мы получили истинное высказывание.
Большинство математических теорем являются импликациями. Однако те импликации, в которых посылки (условия) и заключения (следствия) являются предложениями без взаимной (по существу) связи, не могут играть в науке важной роли. Они являются бесплодными предложениями, так как не ведут к выводам более глубокого содержания.
Логические формулы. Законы алгебры логики
Математики под словом «алгебра» подразумевают науку, которая изучает некие объекты и операции над ними. Например, школьная алгебра (алгебра действительных чисел) изучает действительные числа и операции над ними. Предметом же нашего изучения являются высказывания, операции над ними, а также логические функции. В предыдущих параграфах для обозначения высказываний мы использовали буквы. Как и в алгебре действительных чисел, введем следующие определения.
Определение 9. Логической переменной называется переменная, значением которой может быть любое высказывание.
Логические переменные (далее «переменные») обозначаются латинскими буквами, иногда снабженными индексами, как обычные алгебраические переменные: 
Понятие логической формулы является формализацией понятия сложного высказывания. Введем его индуктивно. Определение 10. Логической формулой является: 1) любая логическая переменная, а также каждая из двух логических констант — 0 (ложь) и 1 (истина); 2) если А и В — формулы, то В и А*В — тоже формулы, где знак «*» означает любую из логических бинарных операций. Формулой является, например, следующее выражение: 
Определение 11. Формулы А и В, зависящие от одного и того же набора переменных 

Для обозначения равносильности формул используется знак равенства, например А В. В дальнейшем будет показано, что любую формулу можно преобразовать к равносильной ей, в которой используются только аксиоматически введенные операции 
1) законы коммутативности
2) законы ассоциативности
3) законы поглощения (нуля и единицы)
4) законы дистрибутивности
5) закон противоречия
6) закон исключенного третьего
7) законы идемпотентности
8) закон двойного отрицания
9) законы де Моргана
10) законы поглощения
Любой из этих законов может быть легко доказан с помощью таблиц истинности.
Пример 2.
Докажем первый закон де Моргана с использованием таблиц истинности. Построим таблицу истинности для левой и правой частей закона.
Так как результирующие столбцы совпали, то формулы, стоящие в левой и правой частях закона, равносильны. Любой из законов алгебры логики может быть доказан путем логических рассуждений.
Пример 3.
Докажем первый закон поглощения 
Пусть истинна правая часть, т. е. 

Пусть истинна левая часть. Тогда по определению дизъюнкции истинна или формула 

Если 

Методы решения логических задач Исходными данными в логических задачах являются высказывания. Эти высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов достаточно трудно.
Многие логические задачи связаны с рассмотрением нескольких конечных множеств и связей между их элементами. Для решения таких задач зачастую прибегают к помощи таблиц или графов, при этом успешность решения во многом зависит от удачно выбранной структуры таблицы или графа. Аппарат же алгебры логики позволяет построить формальный универсальный способ решения логических задач.
Рассмотрим, как можно использовать данный способ для решения задач.
Пример 4.
Задача «Уроки логики». На вопрос, кто из трех учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?
Решение. Обозначим через 


Высказывание 


Пример 5.
Задача «Кто виноват?» По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено: 1) если Иванов не виновен или Петров виновен, то Сидоров виновен; 2) если Иванов не виновен, то Сидоров не виновен. Виновен ли Иванов? Решение. Рассмотрим простые высказывания: А = , В = , С = . Запишем на языке алгебры логики факты, установленные следствием: 

Решить данную задачу — значит указать, при каких значениях А полученное сложное высказывание F истинно. Для этого необходимо проанализировать все строки таблицы истинности, где 



Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Задача про квадрат в треугольнике и 2 способа её решения: с помощью геометрии и с помощью логикиСкачать

Математическая логика, преобразования
Видео:Переставь одну цифру! Задача на логикуСкачать

Теория к заданию 18 из ЕГЭ по информатике
Алгебра логики
Алгебра логики
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Основоположником алгебры логики является английский математик и логик Дж. Буль (1815–1864), положивший в основу своего логического учения аналогию между алгеброй и логикой. Любое высказывание он записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и др.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Например, «3 умножить на 3 равно 9», «Архангельск севернее Вологды» — истинные высказывания, а «Пять меньше трех», «Марс — звезда» — ложные.
Очевидно, что не всякое предложение может быть логическим высказыванием, т. к. не всегда есть смысл говорить о его ложности или истинности. Например, высказывание «Информатика — интересный предмет» неопределенно и требует дополнительных сведений, а высказывание «Для ученика 10-А класса Иванова А. А. информатика — интересный предмет» в зависимости от интересов Иванова А. А. может принимать значение «истина» или «ложь».
Кроме двузначной алгебры высказываний, в которой принимаются только два значения — «истинно» и «ложно», существует многозначная алгебра высказываний. В такой алгебре, кроме значений «истинно» и «ложно», употребляются такие истинностные значения, как «вероятно», «возможно», «невозможно» и т. д.
В алгебре логики различаются простые (элементарные) высказывания, обозначаемые латинскими буквами (A, B, C, D, …), и сложные (составные), составленные из нескольких простых с помощью логических связок, например таких, как «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний.
Обозначим как А высказывание «Алгебра логики успешно применяется в теории электрических схем», а через В — «Алгебра логики применяется при синтезе релейно-контактных схем».
Тогда составное высказывание «Алгебра логики успешно применяется в теории электрических цепей и при синтезе релейно-контактных схем» можно кратко записать как А и В; здесь «и» — логическая связка. Очевидно, что поскольку элементарные высказывания А и В истинны, то истинно и составное высказывание А и В.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
1. Логическое отрицание, инверсия (лат. inversion — переворачивание) — логическая операция, в результате которой из данного высказывания (например, А) получается новое высказывание (не А), которое называется отрицанием исходного высказывания, обозначается символически чертой сверху ($A↖$) или такими условными обозначениями, как ¬, ‘not’, и читается: «не А», «А ложно», «неверно, что А», «отрицание А». Например, «Марс — планета Солнечной системы» (высказывание А); «Марс — не планета Солнечной системы» ($A↖$); высказывание «10 — простое число» (высказывание В) ложно; высказывание «10 — не простое число» (высказывание B ) истинно.
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
| A | ¬A |
| 1 | 0 |
| 0 | 1 |
Высказывание $A↖$ ложно, когда А истинно, и истинно, когда А ложно.
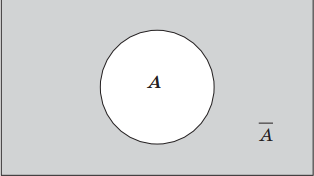
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.
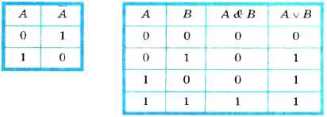
2. Конъюнкция (лат. conjunctio — соединение) — логическое умножение, операция, требующая как минимум двух логических величин (операндов) и соединяющая два или более высказываний при помощи связки «и» (например, «А и В»), которая символически обозначается с помощью знака ∧ (А ∧ В) и читается: «А и В». Для обозначения конъюнкции применяются также следующие знаки: А ∙ В; А & В, А and В, а иногда между высказываниями не ставится никакого знака: АВ. Пример логического умножения: «Этот треугольник равнобедренный и прямоугольный». Данное высказывание может быть истинным только в том случае, если выполняются оба условия, в противном случае высказывание ложно.
Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
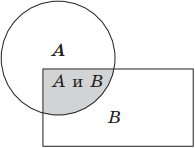
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.
3. Дизъюнкция (лат. disjunction — разделение) — логическое сложение, операция, соединяющая два или более высказываний при помощи связки «или» (например, «А или В»), которая символически обозначается с помощью знака ∨ (А ∨ В) и читается: «А или В». Для обозначения дизъюнкции применяются также следующие знаки: А + В; А or В; А | B. Пример логического сложения: «Число x делится на 3 или на 5». Это высказывание будет истинным, если выполняются оба условия или хотя бы одно из условий.
Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
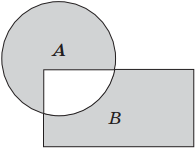
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
4. Дизъюнкция строго-разделительная, сложение по модулю два — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле, которая символически обозначается с помощью знаков ∨ ∨ или ⊕ (А ∨ ∨ В, А ⊕ В) и читается: «либо А, либо В». Пример сложения по модулю два — высказывание «Этот треугольник тупоугольный или остроугольный». Высказывание истинно, если выполняется какое-то одно из условий.
Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
5. Импликация (лат. implisito — тесно связываю) — логическая операция, соединяющая два высказывания при помощи связки «если. то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность». Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием. Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь. Например, «Если 3 * 3 = 9 (А), то Солнце — планета (В)», результат импликации А → В — ложь.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
6. Эквивалентность, двойная импликация, равнозначность (лат. aequalis — равный и valentis — имеющий силу) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В, которое читается: «А эквивалентно B». Для обозначения эквивалентности применяются также следующие знаки: ⇔, ∼. Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Примером эквивалентности является высказывание: «Треугольник будет прямоугольным тогда и только тогда, когда один из углов равен 90 градусам».
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖ ∧B) ∧ (A ∧ B↖)$ |
| Импликация | А → В | $A↖ ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖ ∧ B↖) ∨ (A ∧ B)$ |
Приоритет выполнения логических операций следующий: отрицание («не») имеет самый высокий приоритет, затем выполняется конъюнкция («и»), после конъюнкции — дизъюнкция («или»).
С помощью логических переменных и логических операций любое логическое высказывание можно формализовать, т. е. заменить логической формулой. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определять истинность или ложность составного высказывания. Например, высказывание «Если пять больше двух (А), то вторник всегда наступает после понедельника (В)» — импликация А → В, и результат операции в данном случае — «истина». В логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Рассмотрим, например, построение составного высказывания из высказываний А и В, которое было бы ложно тогда и только тогда, когда оба высказывания истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А высказывание может быть, например, таким: «Этот мяч полностью красный или полностью синий». Следовательно, если утверждение А «Этот мяч полностью красный» — истина, и утверждение В «Этот мяч полностью синий» — истина, то составное утверждение — ложь, т. к. одновременно и красным, и синим мяч быть не может.
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X 3) ∨ (1 3) ∨ (12 3) ∨ (3 2) → (X > 5)) .
Решение. Операция отрицания применена ко всему выражению ((X > 2) → (X > 5)) , следовательно, когда выражение ¬((X > 2) → (X > 5)) истинно, выражение ((X > 2) →(X > 5)) ложно. Поэтому необходимо определить, для каких значений X выражение ((X > 2) → (X > 5)) ложно. Операция импликации принимает значение «ложь» только в одном случае: когда из истины следует ложь. А это выполняется только для X = 3; X = 4; X = 5.
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Под логическим выражением следует понимать такую запись, которая может принимать логическое значение «истина» или «ложь». При таком определении среди логических выражений необходимо различать:
- выражения, которые используют операции сравнения («больше», «меньше», «равно», «не равно» и т. п.) и принимают логические значения (например, выражение а > b , где а = 5 и b = 7, равно значению «ложь»);
- непосредственные логические выражения, связанные с логическими величинами и логическими операциями (например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина).
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a — π/b) a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) b a + a b > a + b, после подстановки получим: 3 2 + 2 3 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (b a + a b > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
4) sin(π/a — π/b) =1» (значение дизъюнкции равно 1, если сумма двух операндов больше или равна 1). Знак «&» на схеме И является сокращенной записью английского слова and.
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы $↖ ∧ X2 ∨ ↖ ∨ X1$.
| X1 | X2 | $↖$ | $↖$ X2 | X1 ∧ X2 | $↖$ | $↖$ ∧ X2 ∨ $↖$ | $↖$ ∧ X2 ∨ $↖$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
- в таблице истинности функции выбирают наборы аргументов, для которых логические формы равны 1 («истина»);
- все выбранные логические наборы как логические произведения аргументов записывают, последовательно соединив их между собой операцией логической суммы (дизъюнкции);
- для аргументов, которые являются ложными, в построенной записи проставляют операцию отрицания.
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ $↖$ ∧ $↖$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
- в таблице истинности выбирают наборы аргументов, для которых логические формы равны 0 («ложь»);
- все выбранные логические наборы как логические суммы аргументов записывают последовательно, соединив их между собой операцией логического произведения (конъюнкции);
- для аргументов, которые являются истинными, в построенной записи проставляют операцию отрицания.
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ $↖$ ∧ $↖$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ $↖$ ∧ $↖$ ∨ X2 = X1 ∧ $↖$ ∨ X1 ∧ X2 ∨ $↖$ ∧ $↖$ ∨ $↖$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ $↖$ ∧ $↖$ ∨ 0 = X1 ∧ X2 ∨ $↖$ ∧ $↖$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | $↖$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ $↖$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ $↖$ ∧ X2 = X2 ∧ (X1 ∨ $↖$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | $↖$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ $↖$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ $↖$ ∧ $↖$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ $↖$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $↖$ ∪ X1 ∧ $↖$ ∧ $↖$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ $↖$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $↖$ ∨ X1 ∧ $↖$ ∧ $↖$ = X2 ∧ X3 ∧ (X1 ∨ $↖$) ∨ X1 ∧ $↖$ ∧ (X2 ∨ $↖$) = X2 ∧ X3 ∨ X1 ∧ $↖$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
Решение. Очевидно, что результатом решения будет таблица, в которой искомая функция Y(X1, X2, X3) будет иметь значение «истина», если какие-либо две переменные имеют значение «истина».
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Из условия 4 следует, что Борис не увлекается ни лыжами, ни теннисом, а из условий 3 и 5, что Петр не умеет играть в футбол, хоккей, теннис и бадминтон. Следовательно, любимые виды спорта Петра — лыжи и плавание. Занесем это в таблицу, а оставшиеся клетки столбцов «Лыжи» и «Плавание» заполним нулями.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
Из условий 1 и 2 следует, что Борис не футболист. Таким образом, в футбол играет Алексей. Продолжим заполнять таблицу. Внесем в пустые ячейки строки «Алексей» нули.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.
Видео:ЗАКОНЫ АЛГЕБРЫ ЛОГИКИСкачать

Алгебра логики знаки и их обозначения
Обозначения в логических операциях
Обозначения для логических связок:
отрицание (инверсия, логическое НЕ) обозначается ¬ (например, ¬А);
конъюнкция (логическое умножение, логическое И) обозначается /
дизъюнкция (логическое сложение, логическое ИЛИ) обозначается /
следование (импликация) обозначается → (например, А → В);
тождество обозначается ≡ (например, A ≡ B). Выражение A ≡ B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны, либо они оба ложны);
символ 1 (единица) используется для обозначения истины (истинного высказывания);
символ 0 (ноль) используется для обозначения лжи (ложного высказывания).
Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) / В равносильны, а А / В и А / В – нет (значения выражений разные, например, при А = 1, В = 0).
Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А / В / С / D означает то же, что и
Возможна запись А / В / С вместо (А / В) / С. То же относится и к конъюнкции: возможна запись А / В / С вместо (А / В) / С.
Свойства логических операций
Общие свойства логических операций
Для набора из n логических переменных существует ровно 2n различных значений. Таблица истинности для логического выражения от n переменных содержит n+1 столбец и 2n строк.
Дизъюнкция
Если хоть одно из подвыражений, к которым применяется дизъюнкция, истинно на некотором наборе значений переменных, то и вся дизъюнкция истинна для этого набора значений.
Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже истинна.
Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже ложна.
Значение дизъюнкции не зависит от порядка записи подвыражений, к которым она применяется.
Конъюнкция
Если хоть одно из подвыражений, к которым применяется конъюнкция, ложно на некотором наборе значений переменных, то и вся конъюнкция ложна для этого набора значений.
Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то конъюнкция этих выражений тоже истинна.
Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то конъюнкция этих выражений тоже ложна.
Значение конъюнкции не зависит от порядка записи подвыражений, к которым она применяется.
Простые дизъюнкции и конъюнкции
Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.
Простая конъюнкция принимает значение 1 (истина) ровно на одном наборе значений переменных.
Простая дизъюнкция принимает значение (ложь) ровно на одном наборе значений переменных.
Импликация
Импликация A →B равносильна дизъюнкции (¬А) / В. Эту дизъюнкцию можно записать и так: ¬А / В.
Импликация A →B принимает значение 0 (ложь) только если A=1 и B=0. Если A=0, то импликация A →B истинна при любом значении B.
Ключевые слова:
- алгебра логики
- высказывание
- логическая операция
- конъюнкция
- дизъюнкция
- отрицание
- логическое выражение
- таблица истинности
- законы логики
1.3.1. Высказывание

Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.

Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и «Two plus six Is eight» можно однозначно сказать, что они истинны. Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.

Например, предложение «Это предложение является ложным» не является высказыванием, так как относительно него нельзя сказать, истинно оно или ложно, без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит сказанному. Если же принять, что предложение ложно, то отсюда следует, что оно истинно.
Относительно предложения «Компьютерная графика — самая интересная тема в курсе школьной информатики» также нельзя однозначно сказать, истинно оно или ложно. Подумайте сами почему.

Например, не являются высказываниями такие предложения, как: «Запишите домашнее задание», «Как пройти в библиотеку?», «Кто к нам пришёл?».

Примерами высказываний могут служить:
- «Na — металл» (истинное высказывание);
- «Второй закон Ньютона выражается формулой F=m•а» (истинное высказывание);
- «Периметр прямоугольника с длинами сторон a и b равен а • b» (ложное высказывание).
Не являются высказываниями числовые выражения, но из двух числовых выражений можно составить высказывание, соединив их знаками равенства или неравенства. Например:
- «3 + 5 = 2 • 4» (истинное высказывание);
- «II + VI > VIII» (ложное высказывание).
Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «X n — 1;
провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
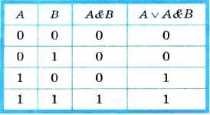
Построим таблицу истинности для логического выражения A ∨ А & В. В нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:
Наборы входных переменных — это целые числа от О до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11. Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение A ∨ А & Б равносильно логическому выражению А.
1.3.4. Свойства логических операций
Рассмотрим основные свойства (законы) алгебры логики.
- Переместительный (коммутативный) закон
- для логического умножения:
для логического сложения:
Сочетательный (ассоциативный) закон
- для логического умножения:
для логического сложения:
(A ∨ B) ∨ C = A ∨(B ∨ C).
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
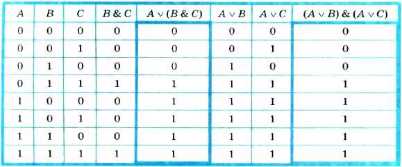
Распределительный (дистрибутивный) закон
- для логического умножения:
для логического сложения:
A ∨ (B & С) = (A ∨ В) & (A ∨ С).
Двойное отрицание исключает отрицание.
Закон исключения третьего
- для логического умножения:
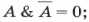
для логического сложения:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
Закон повторения
- для логического умножения:
для логического сложения:
Законы операций с 0 и 1
- для логического умножения:
для логического сложения:
A ∨ O = A; A ∨ l = l.
Законы общей инверсии
- для логического умножения:
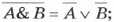
для логического сложения:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности.
Докажем распределительный закон для логическического сложения:
A ∨ (В & С) = (А ∨ В) & (A ∨ С).
Совпадение столбцов, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Пример 2. Найдём значение логического выражения 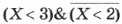
Решение. При X = 0 получаем следующее логическое выражение: 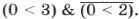
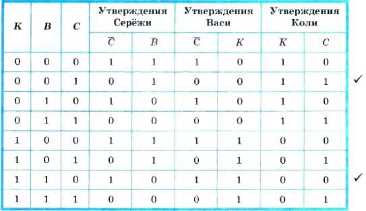
1 С учётом того, что ваза разбита одним внуком, можно было составлять не всю таблицу, а только её фрагмент, содержащий следуюнще наборы входных переменных: 001, 010, 100.
Исходя из того, что знает о внуках бабушка, следует искать в таблице строки, содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10). Таких строк в таблице оказалось две (они отмечены галочками). Согласно второй из них, вазу разбили Коля и Вася, что противоречит условию. Согласно первой из найденных строк, вазу разбил Серёжа, он же оказался хитрецом. Шутником оказался Вася. Имя правдивого внука — Коля.
Задача 2. В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения о возможных победителях:
- Сима будет первой, Валя — второй;
- Сима будет второй, Даша — третьей;
- Алла будет второй, Даша — четвёртой.
По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах?
Решение. Рассмотрим простые высказывания:
C1 = «Сима заняла первое место»;
В2 = «Валя заняла второе место»;
С2 = «Сима заняла второе место»;
Д3 = «Даша заняла третье место»;
А2 = «Алла заняла второе место»;
Д4 = «Даша заняла четвёртое место».
Так как в каждом из трёх предположений одно из высказываний истинно, а другое ложно, то можно заключить следующее:
Логическое произведение истинных высказываний будет истинным:
На основании распределительного закона преобразуем левую часть этого выражения:
Высказывание С1 • С2 означает, что Сима заняла и первое, и второе места. Согласно условию задачи, это высказывание ложно. Ложным является и высказывание В2 • С2. Учитывая закон операций с константой 0, запишем:
Дальнейшее преобразование левой части этого равенства и исключение заведомо ложных высказываний дают:
Из последнего равенства следует, что С1 = 1, Д3 = 1, А2 = 1. Это означает, что Сима заняла первое место, Алла — второе, Даша — третье. Следовательно, Валя заняла четвёртое место.
Познакомиться с другими способами решения логических задач, а также принять участие в Интернет-олимпиадах и конкурсах по их решению вы сможете на сайте «Математика для школьников» (http://www.kenqyry.com/).
На сайте http://www.kaser.com/ вы сможете скачать демонстрационную версию очень полезной, развивающей логику и умение рассуждать логической головоломки Шерлок.
1.3.6. Логические элементы
Алгебра логики — раздел математики, играющий важную роль в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Вы уже знаете, что любая информация может быть представлена в дискретной форме — в виде фиксированного набора отдельных значений. Устройства, которые обрабатывают такие значения (сигналы), называются дискретными. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.
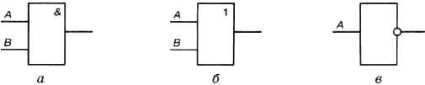
На рис. 1.5 приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и инверсию.
Рис 1.5.
Логические элементы
Логический элемент И (конъюнктор) реализует операцию логического умножения (рис. 1.5, а). Единица на выходе этого элемента появится только тогда, когда на всех входах будут единицы.
Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (рис. 1.5, б). Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица.
Логический элемент НЕ (инвертор) реализует операцию отрицания (рис. 1.5, в). Если на входе элемента О, то на выходе 1 и наоборот.
Компьютерные устройства, производящие операции над двоичными числами, и ячейки, хранящие данные, представляют собой электронные схемы, состоящие из отдельных логических элементов. Более подробно эти вопросы будут раскрыты в курсе информатики 10-11 классов.
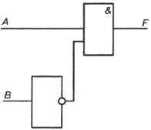
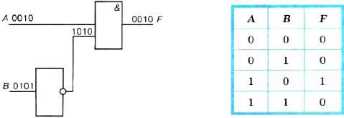
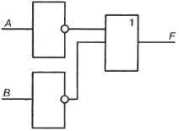
Пример 3. Проанализируем электронную схему, т. е. выясним, какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах.
Решение. Все возможные комбинации сигналов на входах А к В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную схему.
Таблицу истинности можно построить и по логическому выражению, соответствующему электронной схеме. Последний логический элемент в рассматриваемой схеме — конъюнктор. В него поступают сигналы от входа Л и от инвертора. В свою очередь, в инвертор поступает сигнал от входа В. Таким образом,
Составить более полное представление о логических элементах и электронных схемах вам поможет работа с тренажёром «Логика» (http://kpolyakov. narod. ru/prog/logic. htm).
Самое главное
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.
Таблицы истинности для основных логических операций:
При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций:
Вопросы и задания
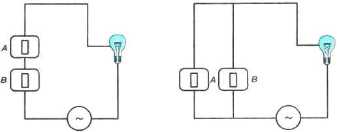
Рассмотрите представленные на рисунке электрические схемы:
На них изображены известные вам из курса физики параллельное и последовательное соединения переключателей. В первом случае, чтобы лампочка загорелась, должны быть включены оба переключателя. Во втором случае достаточно, чтобы был включён один из переключателей. Попытайтесь самостоятельно провести аналогию между элементами электрических схем и объектами и операциями алгебры логики:

Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот её фрагмент:
По запросу сомики & гуппи было найдено 0 сайтов, по запросу сомики & меченосцы — 20 сайтов, а по запросу меченосцы & гуппи — 10 сайтов.
Сколько сайтов будет найдено по запросу сомики | меченосцы | гуппи?
Для скольких сайтов рассматриваемого сегмента ложно высказывание «Сомики — ключевое слово сайта ИЛИ меченосцы — ключевое слово сайта ИЛИ гуппи — ключевое слово сайта»?
Постройте таблицы истинности для следующих логических выражений:
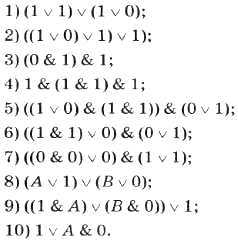
Найдите значение логического выражения 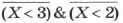
Пусть А = «Первая буква имени — гласная», В = «Четвёртая буква имени согласная». Найдите значение логического выражения 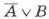
Разбирается дело Джона, Брауна и Смита. Известно, что один из них нашёл и утаил клад. На следствии каждый из подозреваемых сделал два заявления:
Смит: «Я не делал этого. Браун сделал это».
Джон: «Браун не виновен. Смит сделал это».
Браун: «Я не делал этого. Джон не делал этого».
Суд установил, что один из них дважды солгал, другой дважды сказал правду, третий один раз солгал, один раз сказал правду. Кто из подозреваемых должен быть оправдан?
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Электронное приложение к уроку
 |  |  |
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |
Cкачать материалы урока
Специально созданный для целей логики язык получил название формализованного. Слова обычного языка заменяются в нем отдельными буквами и различными специальными символами. Формализованный язык — это «насквозь символический» язык, в котором нет ни одного слова обычного языка. В формализованном языке содержательные выражения заменяются буквами, а в качестве логических символов (логических постоянных) используются символы со строго определенным значением.
В логической литературе используются различные системы обозначений, поэтому ниже даются два и более вариантов символов.
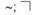
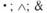
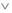

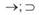
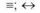
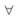
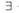
L, N, — знаки для обозначения модального оператора необходимости; читаются: «необходимо, что»;
М — знак для обозначения модального оператора возможности; читается: «возможно, что».
Наряду с перечисленными, в многообразных системах логики используются и другие специфические символы, при этом каждый раз разъясняется, что именно тот или иной символ обозначает и как он читается.
В качестве знаков препинания в искусственных языках логики используются, как и в языке математики, скобки.
А) «Тот, кто ясно мыслит, ясно говорит» — 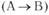
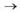
Б) «Он — образованный человек и неправда, что он не знаком с сонетами Шекспира» — 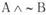
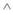
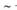
В) «Если свет имеет волновую природу, то, когда он представляется в виде потока частиц (корпускул), допускается ошибка» — 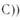
Г) «Если вы были в Париже, то вы видели Лувр или видели Эйфелеву башню» — 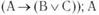
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10605 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
📺 Видео
ЖЕСТКАЯ задача на логику! Попробуй решить!Скачать

🔥 ФОКУС с треугольником #shortsСкачать

A.2.19 Полином ЖегалкинаСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Математика это не ИсламСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Решали пол-урока, а оказалось очень простоСкачать

Треугольники. 7 класс.Скачать

Первый признак равенства треугольников. 7 класс.Скачать

Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать

Задача, которую исключили из экзамена в АмерикеСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Треугольники. Практическая часть - решение задачи. 7 класс.Скачать