В треугольник abc вписана окружность радиуса 4 касающаяся стороны ac

2021-11-23
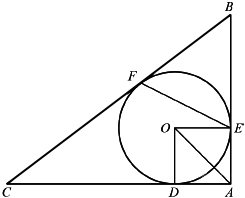
Сторона $AC$ треугольника $ABC$ больше стороны $AB$. Вписанная в треугольник окружность касается стороны $BC$ в точке $M$, а вневписанная — в точке $N$.
а) Докажите, что $MN=AC-AB$.
б) Найдите расстояние между центрами указанных окружностей, если сумма их радиусов равна 24, а $MN=10$.

а) Пусть $BC=a$, $AC=b$, $AB=c$, $p=frac$ — полупериметр треугольника, а вневписанная окружность касается продолжений сторон $AB$ и $AC$ в точках $K$ и $L$ соответственно (рис.1). Тогда

Аналогично докажем, что $BM=p-b=frac$. Следовательно,

б) Пусть $O$ -центр вписанной окружности треугольника $ABC$ (рис.2), $O_$ — центр вневписанной окружности, касающейся стороны $BC$. Радиусы $OM$ и $O_N$ этих окружностей параллельны, т.к. они перпендикулярны одной и той же прямой $BC$.
Пусть $H$ — основание перпендикуляра, опущенного из точки $O_$ на прямую $OM$. Тогда $MNO_H$ — прямоугольник, поэтому

Из прямоугольного треугольника $OHO_$ находим, что

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке M , причём AM = 5R, CM = 1, 5R А)докажите что треугольник ABC прямоугольный Б) найдите расстояние между центрам его вписан?

Алгебра | 10 — 11 классы

В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке M , причём AM = 5R, CM = 1, 5R А)докажите что треугольник ABC прямоугольный Б) найдите расстояние между центрам его вписанной и описанной окружностей , если известно что R = 4.

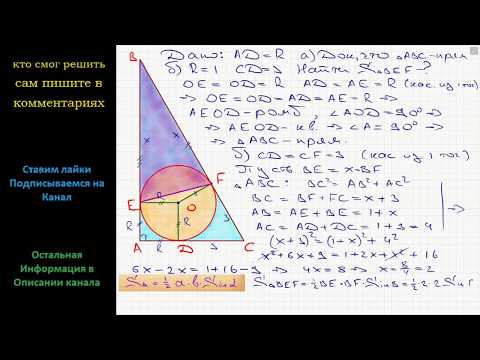
А) Пусть O – центр окружности.

Центр окружности, вписанной в

угол, лежит на биссектрисе этого угла.

АО – биссектриса угла BAC.

прямоугольный и равнобедренный треугольник, его угол OAD равен 45°.

Следовательно, угол BAC равен 90°.

Согласно теореме о равенстве отрезков касательных,

проведённых к окружности из одной точки, AE = AD = 5, CF = CD = 15 и BE = BF.

Пифагора, BC² = AC² + AB².

(15 + x)² = 20² + (5 + x)².

Следовательно, BC = 25.

Sin ∠ABC = AC / BC = 20 / 25 = 4 / 5.

S △BEF = ½ BE * BF sin ∠ABC = ½ * 10 * 10 * 4 / 5 = 40.

Видео:Задача о треугольнике из тренировочного варианта ЕГЭСкачать

Сторона равностороннего треугольника вписанного в окружность равна 12?

Сторона равностороннего треугольника вписанного в окружность равна 12.

Найдите радиус окружности.

Видео:Геометрия В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причёмСкачать

Периметр равнобедренного треугольника КАР с основанием АР равен 32?

Периметр равнобедренного треугольника КАР с основанием АР равен 32.

Вписанная в треугольник окружность касается боковой стороны РК в точке В, причем ВР = 6.

Найдите радиус окружности.

Видео:✓ Простое решение красивой геометрии | Планиметрия | Физтех-2021. Математика | Борис ТрушинСкачать

Укажите в ответе номера верных утверждений : 1 )центром вписанной окружности треугольника является точка пересечения его высот?

Укажите в ответе номера верных утверждений : 1 )центром вписанной окружности треугольника является точка пересечения его высот.

2)центром вписанной окружности треугольника является точка пересечения его медиан.

3) центром вписанной окружности является точка пересечения его биссектрис.

4)центром описанной окружности треугольника является точка пересечения его высот.

5) центром описанной окружности треугольника является точка пересечения его медиан.

6) центром описанной окружности треугольника является точка пересечения его биссектрис.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Окружность, вписанная в треугольник ABC, площадь которого равна 66, касается средней линии, параллельной стороне BC?

Окружность, вписанная в треугольник ABC, площадь которого равна 66, касается средней линии, параллельной стороне BC.

Известно что BC = 11.

Найдите сторону AB.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Периметр прямоугольного треугольника равен 12см?

Периметр прямоугольного треугольника равен 12см.

Найти радиус вписанной окружности если известно что стороны треугольника образуют арифметическую прогрессию.

Видео:11.46.1. Планиметрия. Гордин Р.К.Скачать

Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 120°, а расстояние от центра окружности до вершины этого угла равно с?

Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 120°, а расстояние от центра окружности до вершины этого угла равно с.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

В треугольнике ABC уголC = 90 градусов, AC = 36, BC = 10, 5?

В треугольнике ABC уголC = 90 градусов, AC = 36, BC = 10, 5.

Найдите радиус вписанной окружностям.

Видео:РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Треугольник abc вписан в окружность с центром o?

Треугольник abc вписан в окружность с центром o.

Найдите градусную меру угла с треугол ABC если угол AOB равен 167 градус.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

В прямоугольном треугольнике abc с прямым углом c известны катеты ac = 6 bc = 8найдите радиус окружности, вписанной в треугольнике abc?

В прямоугольном треугольнике abc с прямым углом c известны катеты ac = 6 bc = 8

найдите радиус окружности, вписанной в треугольнике abc.

Видео:ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

В треугольнике ABC AC = 8, BC = 6, угол C равен 90°?

В треугольнике ABC AC = 8, BC = 6, угол C равен 90°.

Найдите радиус вписанной окружности.

На этой странице вы найдете ответ на вопрос В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке M , причём AM = 5R, CM = 1, 5R А)докажите что треугольник ABC прямоугольный Б) найдите расстояние между центрам его вписан?. Вопрос соответствует категории Алгебра и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Видео:Найти радиус за 1 минуту!Скачать

Задание №16 ЕГЭ (профильный уровень)

В прямоугольный треугольник АВС с прямым углом А

и катетами АВ = 3; АС = 5 вписан квадрат ADEF.
а) Докажите, что треугольники BDE и EFC подобны.
б) Найдите отношение площади треугольника EFC к площади квадрата ADEF.

2. Вневписанная в треугольник АВС окружность касается его боковой стороны и продолжения основания АС.

а) Докажите, что радиус этой окружности равен высоте ВН треугольника АВС.

б) Найдите площадь треугольника АВС, если радиус окружности равен 8, а АС·АВ = 120.

3. Две окружности касаются внешним образом в точке L. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.

а) Докажите, что прямые AD и BC параллельны.

б) Найдите площадь треугольника ALB, если известно, что радиусы окружностей равны 8 и 2.

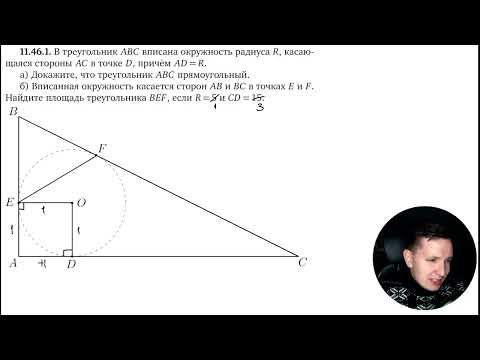
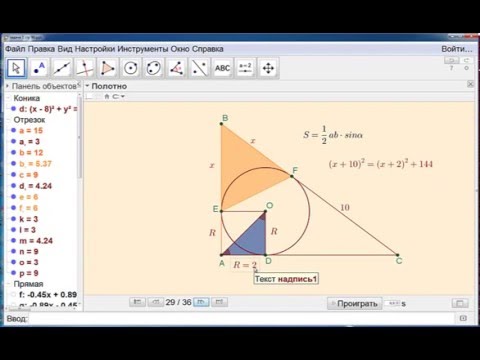
4. В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причём AD= r.

а) Докажите, что треугольник ABC прямоугольный.

б) Вписанная окружность касается сторон AB и BC в точках M и N. Найдите площадь треугольника BMN, если известно, что r= 1 и CD =3.

5. Дан треугольник АВС. Серединный перпендикуляр к стороне АВ пересекается с биссектрисой угла ВАС в точке К, лежащей на стороне ВС.

а) Докажите, что АС2 =ВС·СК.

б) Найдите радиус окружности, вписанной в треугольник АКС, если sinВ = 0,8 и сторона АС= 30.

🎥 Видео

9.52.1. Планиметрия. Гордин Р.К.Скачать

Радиус описанной окружностиСкачать

Задача 16. ЕГЭ по математике. Профиль. Урок 1Скачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

ЕГЭ Математика Задание 6#27935Скачать

№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать