В треугольник abc вписана окружность к окружности проведена касательная

К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 23, 34. Найдите периметр данного треугольника.

Это задание ещё не решено, приводим решение прототипа.

К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.

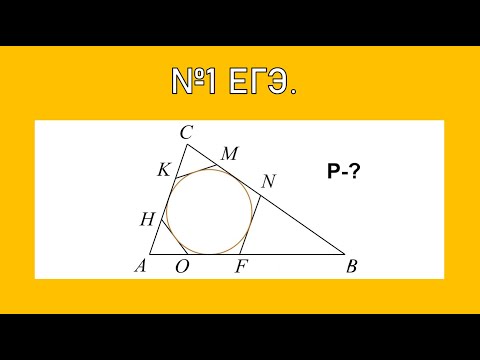
Покажем, что сумма периметров отсеченных треугольников равна сумме длин сторон треугольника АВС, то есть равна его периметру. Отрезки касательных, проведенных к окружности из точек K, H, O, F, N, M соответственно равны друг другу (см. рис., равные отрезки выделены одинаковыми цветами). Поэтому

Видео:Решение задачи №1 из ЕГЭ математикаСкачать

К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно?

Геометрия | 5 — 9 классы

К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно.

Известно, что AB = 33, а периметр треугольника ABC равен 103.

НАйти периметр треугольника CPQ.

Нашел чему равно PQ.

К. PN = PK и KQ = QM (по свойству касательных), то СN + CM = P треуг.

AN = AL и MB = BL, то AN + NB = AB (по св — ву касательных)

ABC = AB + BC + AC, где BC = CM + MB ; AC = CN + AN

Получим : AB + CM + MB + CN + AN = 103 (выделенные величины равно, поэтому их складываем)

AB + 2CM + MB + AN = 103 (см.

Отсюда CM = 51, 5 — 33 = 18, 5

CN + CM = P треуг.

СPQ и CN = CM (по св — ву касат.

CPQ = 2CM = 2 * 18, 5 = 37.

Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Через середину P стороны AB треугольника ABC проведена прямая, параллельная стороне AC и пересекающая сторону BC в точке Q?

Через середину P стороны AB треугольника ABC проведена прямая, параллельная стороне AC и пересекающая сторону BC в точке Q.

Найдите длину стороны AC, если известно, что периметр треугольника ABC равен 54см, QC = 12см, а PQ в два раза больше, чем BP.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

КАСАТЕЛЬНАЯ К ОКРУжНОСТИ , ВПИСАННОЙ В ТРЕУГОЛЬНИК ABC ПЕРЕСЕКАЕТ СТОРОНЫ ВС И АС СООТВЕТСТВЕННО В ТОЧКАХ А1 И В1 ?

КАСАТЕЛЬНАЯ К ОКРУжНОСТИ , ВПИСАННОЙ В ТРЕУГОЛЬНИК ABC ПЕРЕСЕКАЕТ СТОРОНЫ ВС И АС СООТВЕТСТВЕННО В ТОЧКАХ А1 И В1 .

НАЙДИТЕ ПЕРИМЕТР ТРЕУГОЛЬНИКА А1В1С1 ЕСЛИ ВС = 5, АС = 6 И АВ = 7 МОЖНО ТОЛЬКО ОТВЕТ БЕЗ РЕШЕНИЯ!

Видео:№635. Через точку А окружности проведены касательная и хорда, равная радиусу окружности.Скачать

Периметр треугольника ABC равен 8?

Периметр треугольника ABC равен 8.

В треугольник вписана окружность и к ней проведена касательная, параллельная стороне AB.

Отрезок этой касательной, заключённый между сторонами AC и CB, равен 1.

Найдите сторону AB.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В равнобедренный треугольник ABC вписана окружность, касающаяся боковых сторон треугольника в точках K и E?

В равнобедренный треугольник ABC вписана окружность, касающаяся боковых сторон треугольника в точках K и E.

Найдите периметр треугольника ABC, если хорда KE равна 12 см, а отрезок касательной, заключенной между боковыми сторонами и параллельный основанию, равен 10 см.

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Периметр треугольника ABC равен 12см, а длина диаметра окружности , вписанной в него , равна 6 см?

Периметр треугольника ABC равен 12см, а длина диаметра окружности , вписанной в него , равна 6 см.

Вычислите площадь треугольника ABC.

Видео:ЕГЭ 1 задание ✧ К окружности, вписанной в треугольник ABC, проведены три касательные. Найти периметрСкачать

Периметр треугольника abc равен 12 окружность касающаяся стороны AB и продолжение сторон AC и BC касается прямой АС в точке Р?

Периметр треугольника abc равен 12 окружность касающаяся стороны AB и продолжение сторон AC и BC касается прямой АС в точке Р.

К этой окружности проведена касательная параллельная прямой AB и пересекающая продолжение сторон АС и ВС в точках M и N так что MN = 3 НАйдите длину отрезка PQ где Q точка касания вписаной окружности треугольника ABC со стороной AC.

Видео:№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать

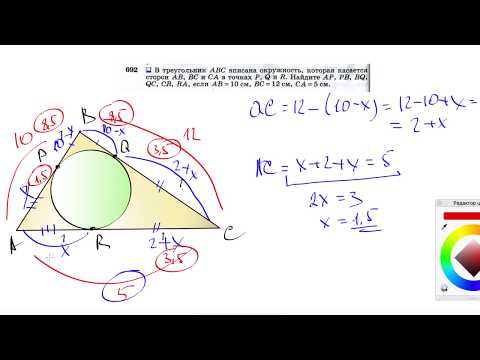
К окружнности, вписанной в треугольник ABC, проведены три касательные?

К окружнности, вписанной в треугольник ABC, проведены три касательные.

Периметры отсеченных треугольников равны 10, 12, 7.

Найдите периметр данного треугольника.

Видео:Задание В6 по математике.Скачать

Окружность радиуса 2, вписанная в треугольник ABC, касается средней линии треугольника, параллельной стороне BC?

Окружность радиуса 2, вписанная в треугольник ABC, касается средней линии треугольника, параллельной стороне BC.

Периметр треугольника ABC равен 24.

Найти стороны треугольника.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Точки T и O — соответственно середины AB и BC треугольника ABC?

Точки T и O — соответственно середины AB и BC треугольника ABC.

В треугольник BTO вписана окружность.

Вычислите длину радиуса окружности, если известно, что площадь треугольника TBO равна 12 см², а периметр треугольника ABC равен 16.

Видео:ЕГЭ 2017 | Задание 3 | К окружности ... ✘ Школа ПифагораСкачать

Треугольник ABC – равносторонний?

Треугольник ABC – равносторонний.

Окружность, вписанная в этот треугольник, касается его сторон в точках M и N .

Длина дуги этой окружности равна 1.

Какой периметр имеет треугольник ABC?

На странице вопроса К окружности, вписанной в трегольник ABC, проведена касательная, пересекающая стороны AC и BC в точках P и Q соответственно? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Трапеция, ее признаки и свойства Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие — боковыми сторонами. . Средняя линия трапеции — отрезок..

Решение в приложении.

Мама за 30 минут прошла 2, 5 км, Юра проехал 6 км. Имеем прямоугольный треугольник с катетами 2, 5 и 6 км. Надо найти гипотенузу. С² = 2, 5² + 6² = 6, 25 + 36 = 72, 25 с = √72, 25 = 8, 5 Ответ : 8, 5 км.

Вот 180 — (65 + 50) = 65 и т. Д На фото.

По — моему, есть ошибка в вопросе.

Пусть х — один из смежных углов, тогда второй угол 180 — х. Биссектриса первого угла — х / 2, второго — (180 — х) / 2 = 90 — (x / 2). Т. к. Биссектрисы выходят из одной точки то угол между ними равен (х / 2) + 90 — (х — 2) = 90. Следовательно, би..

126 градусов, 76 + 50 = 126.

АОВ + ВОР = 76 + 50 = 126 поплидмзмшь.

Розв»язок додала. Вiдповiдь 112см².

10 : 2 = 5 25 : 2 = 12, 5 5 ^ 2 + 12, 5 ^ 2 = 13, 462 ^ 2 13, 462 * 4 = 53, 848.

Видео:Геометрия К окружности, вписанной в треугольник ABC, проведены три касательные (см. рис.)Скачать

Задание №1001

Видео:Разбор Задачи №16 из Работы СтатГрад от 19 апреля 2019Скачать

Условие

К окружности, вписанной в правильный треугольник ABC , проведена касательная, пересекающая стороны AC и BC в точках M и N соответственно и касающаяся окружности в точке T .

а) Докажите, что периметр треугольника MNC равен стороне треугольника ABC .

б) Найдите MT:TN, если известно, что CM: MA=1:4.

Видео:Вписанная окружностьСкачать

Решение

а) Пусть K и L — точки касания окружности и сторон BC и AC соответственно.

Так как MT=ML и NK=NT как отрезки касательных, проведенных из одной точки, то

P_= CM+MT+TN+NC= CM+ML+KN+NC= CL+KC.

Так как ABC — правильный треугольник, то CL=KC=frac. Следовательно, P_=AC, что и требовалось доказать.

б) 1 . Обозначим TN=x, CM=a. Так как CM:MA=1:4 по условию, то MA=4a и AC=5a.

Тогда CL=frac=fraca и ML=CL-CM=fraca-a=fraca. Так как ML=MT, то MT=fraca. Тогда MN=MT+TN=fraca+x.

Так как NT=NK, то NK=x. Тогда CN=CK-NK=frac-x=fraca-x.

2. По теореме косинусов для треугольника MNC

MN^2=CN^2+CM^2- 2 cdot CN cdot CM cdot cos angle NCM. Подставляя в это уравнение выражения для сторон треугольника MNC , получим:

left ( fraca+xright )^2= left ( fraca-xright )^2+a^2-2left ( fraca-xright )a cos 60^circ;

fraca^2+2 cdot fracax+x^2= fraca^2-2 cdot fracax+x^2+a^2- 2left ( fraca-x right )a cdot frac;

📸 Видео

ОКРУЖНОСТИ В ОГЭ ✨ #огэ #математика #егэ #геометрия #окружностьСкачать

Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!Скачать

Секретная теорема из учебника геометрииСкачать

№636. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиесяСкачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

8 класс, 38 урок, Вписанная окружностьСкачать